回路成型最优设计方法在X-29验证机中的应用
刘 浏
(江苏金陵机械制造总厂,南京 211100)
由于飞行器具备非常广泛的应用,最近几十年来,受到了各研究机构的高度关注。飞行器是非常复杂的动力学系统,具有非线性、高耦合、时变等特性,使得为飞行器设计相应的控制系统变得非常困难[1]。而验证机则是一种用于测试新技术可行性的试验型飞机,它所使用的技术往往综合了各学科最新最前沿的技术,目的是为了验证各单项技术的相容性和综合技术方案的可行性[2]。只有经过验证机验证过的技术,才能安全地应用于其他飞机上,这样做不仅减少了型号研制的风险,而且可以提高科研投资的效费比[3]。
近年来,在各研究机构的努力下,用于飞行器的控制方法有了很大的发展,并且出现了很多的成功应用。卡内基梅隆大学的无人直升机研究组采用鲁棒回路成形和增益调度的方法设计控制器[4],并在雅马哈R50上实现。乔治亚理工大学用近似逆模型加神经网络的方法设计控制器[5],该控制器为多回路结构,内环为姿态控制环,外环是速度和位置速度环,该控制器的飞行包线很宽,并且具备良好的轨迹跟踪性能,对飞行器参数的变化具备很好的鲁棒性。斯坦福大学用强化学习的方法设计了一种控制器[6],该方法首先通过学习建立飞行器的动力学模型,然后再通过学习的方法设计飞行器特技飞行控制器,该控制器能够使飞机实现翻转飞行等一系列特技动作。
在众多的设计方法中,回路成型是比较受关注的设计方法[1,7-8],该方法不仅能够处理多输入多输出系统,还能处理系统模型中的不确定性,有较为固定的设计步骤,设计过程比较简单,并且使用稳定裕度作为设计目标,设计任务明确。
1 系统建模
X-29是X系列试验飞行器中十分重要的一员,用于试验前掠翼技术以及为达到下一代战斗机所要求的高机动性、轻重量、低成本、高效率而应用的其它先进技术[9-11]。前掠翼布局具有优越的气动性能,可大大提高飞机的低速操纵性能,显著减小跨声速飞行时的阻力并增强机动性,在大迎角下具有良好的失速特性和横航向可控制性[12-13]。
X-29的简化系统模型[14-15]如图1所示,控制方式为由鸭翼和襟副翼来控制倾斜角和攻击角,倾斜角θ是机轴与水平线的夹角,攻击角α是机轴与飞机速度之间的夹角,飞行路径角γ=θ-α是速度与水平线之间的夹角,三者之间的关系如图2所示。

图1 X-29简化系统模型Fig.1 Simplified system model of X-29

图2 倾斜角、攻击角和飞行路径角Fig.2 Pitch angle,attack angle and flight angle
在文献[16]中,建立了3种不同的系统模型,第一种是以鸭翼的转动作为输入,以攻击角的变化作为输出。第二种是以鸭翼的转动作为输入,以倾斜角的变化作为输出。第三种是以鸭翼和襟副翼的变化作为输入来控制倾斜角和攻击角的变化。在本文中,考虑第一种系统模型,建模为一个单输入单输出系统,被控对象简化模型的传递函数为[17]

由于系统是不稳定的和非最小相位的,因而设计控制器使得系统稳定并具有一定的性能指标比较困难。
2 控制器的设计
本文采用最简单的回路成型设计方法,在保持系统内稳定要求的前提下设计一个最小控制误差的控制器,图3是一个典型的单输入单输出系统,其中 C(s)为所设计的飞行器控制器,P(s)为被控验证机的系统模型,取回路开环传递函数为[17]


图3 闭环控制系统Fig.3 Closed-loop control system
飞行器控制系统有2个性能要求,在保证系统是内稳定的条件下使得‖S‖∞是最小的。根据性能要求建立的代价函数为

作为控制系统,首先要保证系统的稳定性,在稳定基础上才能保证系统的其他性能要求。系统回路参数ωc的选择范围可由劳斯稳定判据来求得,控制系统的闭环传递函数为

可以得到控制系统的特征多项式为

式中:a3=0.016;a2=15.904-ωc;a1=10ωc-96;a0=96ωc
由劳斯稳定判据得:

由此可以得到使系统内稳定的ωc取值范围为9.85<ωc<15.5。进一步简化带约束条件的最优控制器性能代价函数为

在Matlab中,我们先用无穷范数命令norm(F,inf)来对灵敏度函数S进行处理,求出带参的无穷模函数,然后以这个关于ωc的函数作为简化的性能代价函数,求出最优的控制器参数,部分Matlab代码为

然后把得到的关于ωc的函数作为新目标函数,求出它的带约束最优解:

得到最优控制器的参数为
对于求解上述的最优控制器设计问题,因为含有2个变量,且系统阶数较高,不易通过求导方式得到。所以,在本文中,我们使用Matlab最优化工具箱中的fimincon()函数来求解该最优控制器设计问题,该函数的调用格式为


所以可以得出当ωc=13.0677时,灵敏度函数的无穷模‖S‖∞有最小值为13.4262。
此时最优控制器的表达式为

控制器参数最优整定算法流程为


3 仿真试验结果

图4 回路传递函数波特图Fig.4 Bode of loop transfer function
在满足系统稳定性和性能指标的前提下,ωc越大,性能越好,因为这样可以在更宽的频率范围内较小。
当ωc=13.0677时,灵敏度函数和补灵敏度函数的波特图如图5所示,从图中可以看到,在ωc=13.0677的条件下,灵敏度函数的剪切频率约为7.37 rad/s,相角裕度约为207°,在频率为22.5 rad/s时取得幅值22.6 dB,满足系统稳定性的要求。

图5 灵敏度函数和补灵敏度函数波特图Fig.5 Bode of sensitivity function and complementary sensitivity function
当 ωc取 10,11,12,13,14,15 时的灵敏度函数无穷模和波特图如表1和图6所示,从中可以看出当ωc=13.0677时灵敏度函数幅值的无穷模是最小的,误差传递函数的谐振峰值Mr达到最小说明对于跟踪误差的稳定性也是最好的,达到了最优的控制器设计性能指标。

表1 灵敏度函数的无穷模Tab.1 Infinite norm of sensitivity function

图6 不同取值时的灵敏度函数波特图Fig.6 Bode of sensitivity function under different parameters
图 7 为 ωc取 10,11,12,13,14,15 时的闭环系统波特图,表2为闭环系统的频率特性。从图7和表2中可以看到,当ωc=13.0677时,闭环系统传递函数的谐振峰值也是最小的,这表明系统的阻尼系数较小,阶跃响应的超调较小,因而系统的相对稳定性也越好。
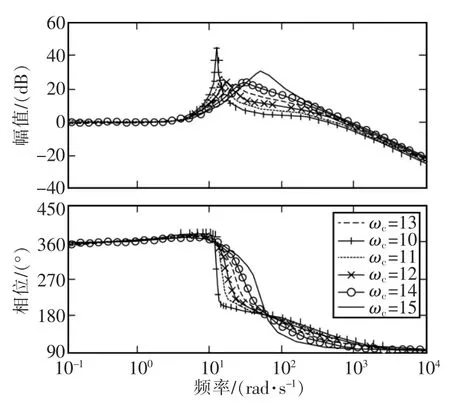
图7 不同取值时的闭环系统波特图Fig.7 Bode of closed-loop system under different parameters

表2 不同取值时的闭环传递函数特性Tab.2 Characteristics of closed-loop transfer function under different parameters
当 ωc取 11,12,13,14 时的闭环系统的阶跃响应、脉冲响应和斜坡响应如图8~图10所示。从图中我们可以看出,对于脉冲和单位阶跃输入,闭环控制系统能够很好地消除稳态误差。而对于单位斜坡输入,虽然不能完全消除稳态误差,但是当ωc=13.0677时系统的稳态误差是最小的。同时考虑系统的调节时间和超调量,得出当ωc=13.0677时系统的综合性能指标是最好的。

图8 不同参数时闭环系统的阶跃响应Fig.8 Step responses of closed-loop system under different parameters

图9 不同参数时闭环系统的脉冲响应Fig.9 Impulse responses of closed-loop system under different parameters

图10 不同参数时闭环系统的斜坡响应Fig.10 Slope responses of closed-loop system under different parameters
4 结语
本文首先对X-29前掠翼验证机进行了分析与建模,在所建立的不稳定和非最小相位模型上,利用回路成型的方法设计了在约束条件下的最优化控制器,在满足系统内稳定的条件下尽可能地减少了闭环系统的稳态误差,达到了要求的性能指标,并通过Matlab验证和比较了所设计控制器,分析了系统的控制特性。仿真试验结果表明所设计的控制器具备良好的稳定性、跟踪性和干扰抑制特性。
[1]DENG Hai-bo,ZHAO Xiao-guang,HOU Zeng-guang,et al.Design of an H-inf loop shaping velocity controller for a small unmanned helicopter[C]//IEEE World Congress on Intelligent Control and Automation,2010:108-113.
[2]J.R.Sitz,T.H.Vernon.Flight control system design factors for applying automated testing techniques[C]//IEEE Digital Avionics Systems Conference,1990:235-247.
[3]M.L.Kerr,C.Y.Lan,S.Jayasuriya.Non-sequential MIMO QFT control of the X-29 aircraft using a generalized formulation[J].International Journal of Robust and Nonlinear Control,2007(17):107-134.
[4]M.La Civita,G.Papageorgiou,W.Messner,et al.Design and flight testing of a gain-scheduled H-inf loop shaping controller for wide-envelope flight of a robotic helicopter[C]//American Control Conference,2003:4195-4200.
[5]D.Bresch-Pietri,M.Krstic.Delay-adaptive predictor feedback for systems with unknown long actuator delay[J].IEEE Transactions on Automatic Control,2010,55(9):2106-2112.
[6]T.Tanaka.Autonomous flight control for a small RC helicopter:a measurement system with an EKF and a fuzzy control via GA-based learning[C]//International Joint Conference,2006:1279-1284.
[7]张清江,王新民,沈宁,等.飞行控制系统鲁棒性定量评估方法研究[J].计算机仿真,2010,27(11):57-61.
[8]C.S.Hsu,D.Hou,G.Robel.A minimal realization algorithm for flight control systems[C]//American Control Conference,1988:2268-2270.
[9]R.Clarke,J.J.Burken,J.T.Bosworth,et al.X-29 flight control system:lessons learned[J].International Journal of Control,1994(50):199-219.
[10]杨熙义.前掠翼验证机X-29A的FBW[J],航空电子技术,1985(3):46-47.
[11]G.J.Davis,A.Patterson-Hine,M.R.Earls,et al.Software reliability evaluation of the X-29A flight control system[C]//Digital Avionics Systems Conference,1992:376-387.
[12]王晋军.鸭翼-前掠翼气动布局纵向气动特性实验研究[J].空气动力学学报,2004,22(2):237-240.
[13]沈冬,张彬乾,陈迎春,等.前掠翼融合体无尾布局流动控制技术[J].航空学报,2009,30(3):397-402.
[14]R.Marie,E.Kreindler.Flight control of an X-29 type aircraft via a combination of LQ optimization techniques[C]//IEEE Conference on Decision and Control,1986:656-660.
[15]C.Y.Huang,G.J.Knowles.Application of nonlinear control strategies to aircraft at high angle of attack[C]//IEEE Conference on Decision and Control,1990:188-193.
[16]W.Quinn.Multivariable control of a forward swept wing aircraft,Laboratory for Information and Decision Systems Report[R],MIT,1986.
[17]J.Doyle,B.Francis,A.Tannenbaum.Feedback control theory[M].Macmillan publishing Co,1990.

