基于分布式电源和需求响应的主动配电网规划

李金炀，唐惠玲

（广东工业大学 物理与光电工程学院，广州 510006）

近年，分布式发电技术得到大力发展。分布式电源的加入使配电网从传统的单一电源网络转变为主动、多电源的复杂配电系统即主动配电网ADN（active distribution network），但增加了电力系统负荷预测、规划和运行的不确定性。为了提高主动配电网的灵活性，可适当地引入需求响应DR（demand response）机制。通过基于主动配电网与DG、用户负荷之间的协调机理，对配电网进行综合规划。

针对含分布式电源的配电网规划，国内外已进行相关研究并取得了很多成果。文献[1-2]将不同种类的分布式电源接入配电网进行选址定容规划，但没能考虑需求侧响应融入电网及对配电网的影响；文献[3]讨论了具体的分布式电源类型和需求响应及其协调优化配置问题，而约束的设置问题欠妥。可见，对含有分布式电源的主动配电网规划还不够全面，需要更全面的研究，特别是融合了需求侧响应对配电网的影响。

本文在主动配电网中引入了分布式电源和需求响应，建立基于分布式电源和融合需求响应的主动配电网规划框架，并利用改进的多目标粒子群算法来进行DG的选址定容，并获得最佳需求侧响应方案。最后，以IEEE-33节点配电系统进行综合性比较验证。

1 基于分布式电源和需求侧响应的综合规划模型

1.1 目标函数

在主动配电网中接入DG并考虑需求侧响应，DG和DSR都能够影响配电网的负荷，在进行系统网络架构规划时便提高了可调控性，系统设计可以更加灵活。针对分布式电源接入AND的定容选址问题寻求最优解，在其可靠、安全的基础上达到经济效益的最大化。本文建立2个优化目标，包括系统经济目标和需求侧响应目标。

1.1.1 系统经济目标

DG加入到配电网中，使配电网运行操作更加灵活。考虑含有DG的单辐射线路，如图1所示。

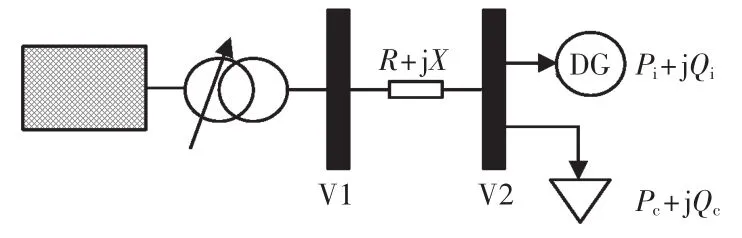
图1 含DG的单辐射线路Fig.1 One single feeder connected with DG

图中：Pi+jQi为DG的注入功率；R+jX为支路阻抗；Pc+jQc为负载消耗。根据图1所示，本文系统的经济目标函数包含系统的网损、分布式电源的投资及运行维护成本、线路运行成本和外购电成本等因素。其表示为

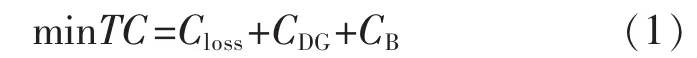
式中：TC为系统的经济总成本；Closs为线路运行和损耗成本；CDG为分布式电源的投资及运行维护成本；CB为外购电成本。

式中：Cs为单位售电价格（元/kW·h）；b为配电网系统的总支路数；plossi为第i条支路的有功网损功率；τmaxi为第i条支路的年最大负荷损耗小时数。

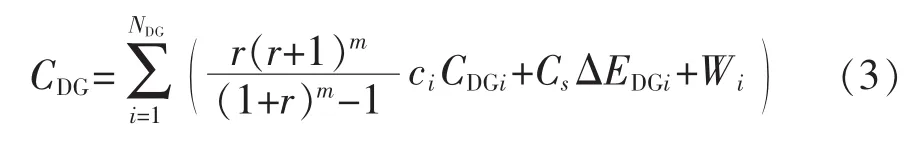
式中：NDG为DG的个数；r为贴现率；m为DG的使用年限；ci为在节点i处接入单位容量DG的投资费用（万元）；CDGi为节点 i处接入 DG 的容量；ΔEDGi为第i个分布式电源总的电量损失值（104kW·h）；Wi为在节点i处接入DG的年运行维护费用（万元）。

1.1.2 需求侧响应目标

电力需求侧响应是指电力用户根据市场电价的变化或者电价的激励机制所做出的响应，从经济性方面改变原来的消费习惯，使得电网的电力负荷分布均衡，提高电网的可靠性。需求侧响应主要包括价格响应和激励响应。价格响应主要指电力用户根据实时电价、分时电价等因素做出响应，包括单一时段响应和多时段响应等形式。激励响应则通过直接控制负荷分布或采用可中断负荷IL（interruptible load）来改变电力用户的用电习惯。

需求侧响应机制是当用电价格升高或系统用电负荷分配不合理引起系统不稳定时，由于用电激励机制电力用户减少的负荷可以获得直接补偿或者用电价格信号改变而使用户改变固有的用电习惯。通过一定的可中断负荷机制，可以削减一部分用户的用电负荷，同时供电方提供直接的缺电补偿。因此建立目标函数：

式中：CDSR为需求侧响应的总成本；τ为计算周期；NL为负荷节点的个数；Caddi（t）和 CCi（t）分别为负荷节点i所增加负荷的单位激励费用和单位缺电补偿费用；Paddi（t）和 PCi（t）分别为负荷节点 i在 t时间内增加和缺失的负荷功率。

故系统整体的目标函数F可表示为

1.2 约束条件

1.2.1 等式约束

式中：PDGi和QDGi分别为节点i所接入分布式电源的有功及无功输出；PLi和QLi分别为节点i处的负载功率；Vi为节点i处的电压幅值；Gij和Bij分别为支路电导和支路导纳；θij为节点i与节点j之间的电源相角差。

1.2.2 不等式约束

1）电压约束

式中：Vmin、Vmax分别为系统节点电压的下限和上限。

2）支路潮流约束

3）需求侧响应约束

式中：Paddimin和Paddimax分别为负荷节点增加的激励负荷在时间段t的上、下限；PCimin和PCimax分别为负荷节点的缺失负荷功率在时间段的上、下限。

2 改进的粒子群算法

近年来粒子群算法PSO在电力系统优化问题中得到了广泛应用。粒子群算法是由Kennedy博士和Eberhart博士提出的一种全局优化进化算法，源于鸟类群体捕食行为的研究，基于种群的并行全局搜索策略，对于大规模优化问题的求解具有较高的收敛速度以及全局寻优能力。

在系统寻优的每一次迭代中，各个粒子根据下列公式更新自己的位置和速度：

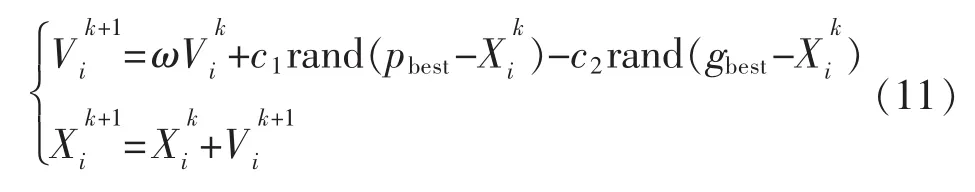
式中：c1，c2为学习因子，一般取 c1=c2=2；ω 为权重系数；rand 为（0，1）之间的随机数；pbest，gbest为粒子本身最优值和整个群体最优值，即局部最优值和全局最优值。

模拟退火算法SA是一种随机寻优方法，在某一较高的初始温度，随着温度参数的不断下降，结合概率突跳特性在搜索空间中寻找目标函数的全局最优解，使其能够从局部最优解中概率性地跳出，从而最终趋向于全局最优。传统的PSO早期的收敛速度比较快，但收敛精度较低，易陷入局部最优。而模拟退火算法能够弥补粒子群算法的不足，将其两者有机地结合，能够在粒子群算法的基础上发挥模拟退火算法的优点，提高计算精度和效率。

本文结合模拟退火算法的优点对粒子群算法进行改进，得到一个新的改进的粒子群算法IMPSO，会根据得到的每个个体的pbest值，结合式（12）表示的Metropolis抽样准则，对pbest值进行优化选择，得出的结果将作为下一代群体中各个粒子的历史最优解，最终以其中最好的解作为改进PSO算法的gbest，其算法流程如图2所示。

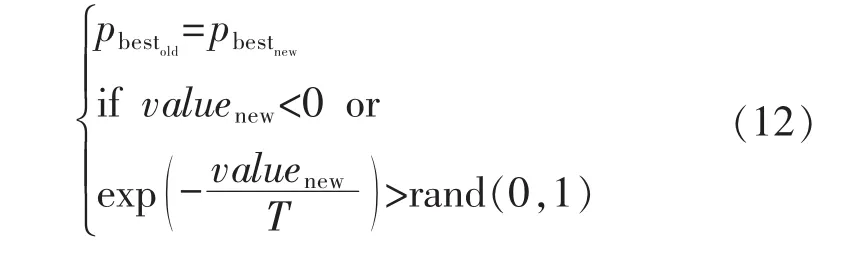
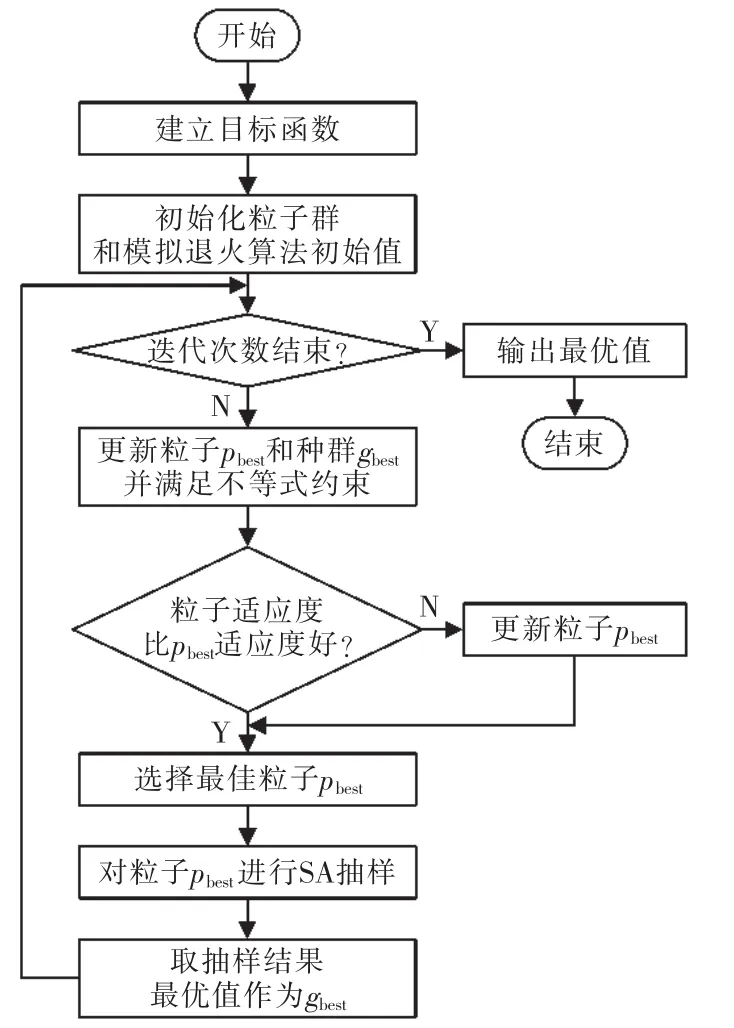
图2 改进粒子群算法流程Fig.2 Flow chart of IMPSO

3 算例分析

本文采用IEEE-33节点配电系统作为算例来进行仿真分析，系统的结构如图3所示。在本系统中，系统的额定电压为12.66 kV，系统总有功负荷为3715 kW，总无功负荷为2300 kvar，节点电压偏移不超过0.05 pu，典型日曲线如图4所示。

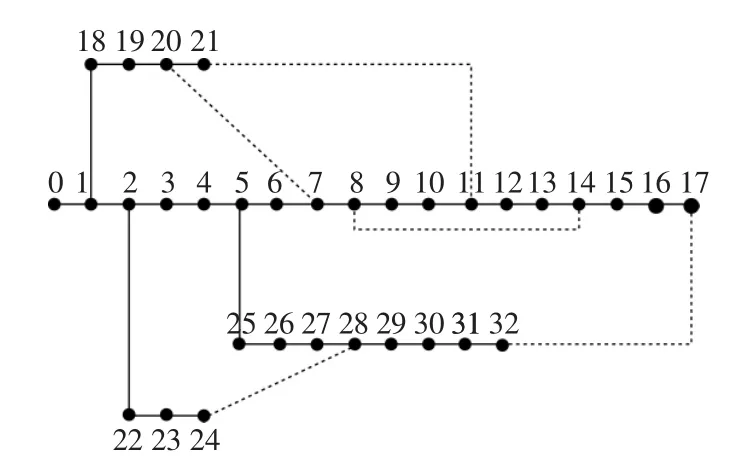
图3 IEEE-33节点配电系统Fig.3 IEEE-33 nodes distribution system

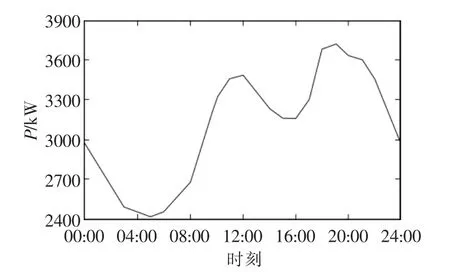
图4 负荷典型日特性曲线Fig.4 Typical daily curve of load

仿真各项参数设置为改进粒子群算法种群规模20，迭代次数取200，退火常数取0.5；DG的功率因数为0.9，假定分布式电源的运行寿命为20 a，贴现率为0.1。采取2种规划方案：仅DG接入的规划和融合了DSR的综合规划，考虑需求侧响应融合前、后DG的定容选址的选取，并通过改进的粒子群算法对主动配电网规划的目标函数进行优化。需求响应系统的DG安装位置和容量如表1所示。

表1 DG安装位置和容量Tab.1 DG’s installation and capacity

表1表明，融合了DSR规划方案使系统所加入分布式电源的容量得到优化。融合DSR的综合规划和仅接入DG的2种规划方案总的费用曲线如图5所示，规划中具体成本费用的对比如表2所示。

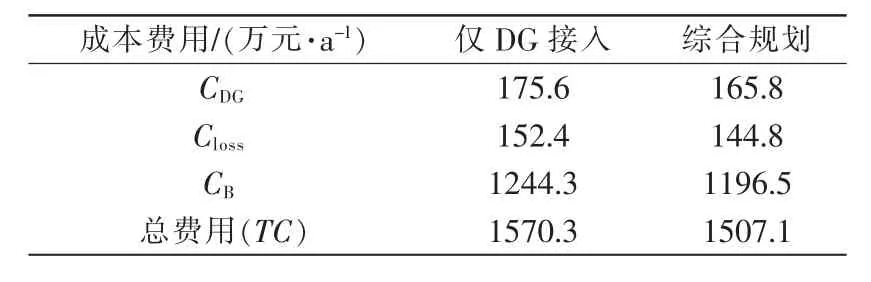
表2 两种规划方案下费用对比Tab.2 Compare the cost of two planning programs

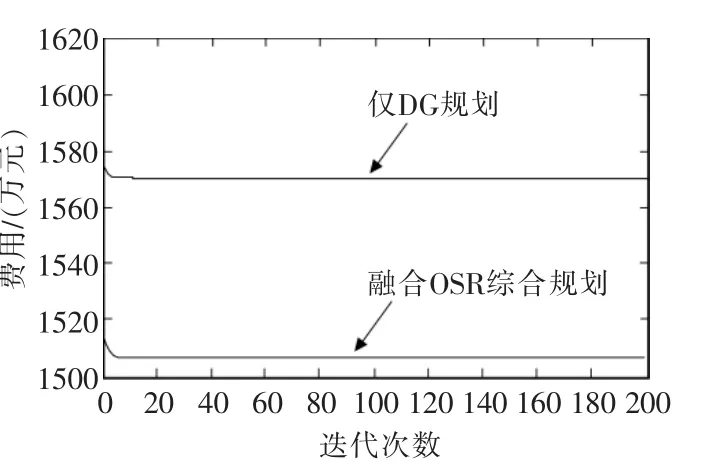
图5 两种方案下的总费用曲线Fig.5 Total cost curves of the two program

通过图5和表2的对比可知，在主动配电网加入分布式电源并融合了需求侧响应，不仅能够优化DG的容量，并且能够有效地降低DG的投资及运行维护成本，同时降低系统的网络损耗进而降低电网的运行成本，提高了系统稳定性，使得配电网的稳定性和经济性都得到了提高。

4 结语

本文在基于分布式电源接入配电网并融合了需求响应的基础上利用改进的粒子群算法对配电网进行综合规划。对不同情况下规划方案的经济性和可靠性的对比分析表明，接入分布式电源同时融合了需求响应的综合规划方案能降低系统网损、提高负荷率，并带来一定的经济效益，同时能够弥补分布式电源间接性出力特性的缺陷，减少DG接入容量，使系统电压更趋于稳定，提高配电网系统的供电可靠性。尤其目前全球面临资源、能源的紧缺，DG的接入能够使得主动配电网实现环境友好型的绿色环保发电，而需求响应的融合则有利于推动节能减排并使电能得到优化使用。随着不断的研究发展，分布式电源技术会更加成熟使其安装使用成本逐步降低，加之需求侧响应的综合规划，这种规划方案在未来会具有更加明显的经济和环境友好优势。

[1]邱晓燕，夏莉丽，李兴源.智能电网建设中分布式电源的规划[J].电网技术，2010，34（4）：7-10.

[2]庄雷明.城市电网规划中分布式电源容量的优化配置[D].北京：华北电力大学，2010.

[3]Sheikhi Fini A，Parsa Moghaddam M，Sheikh-El-Esl-ami M K.An investigation on the impacts of regulatory support schemes on distributed energy resource expansion planning[J].Renewable Energy，2013（53）：339-349.

[4]张勇，吴淳.分布式发电机在配电网中的优化配置[J].电力系统保护与控制，2010，38（11）：33-34.

[5]H.A.Aalami，M.Parsa Moghaddam，G.R.Yousefi.Demand response modeling considering Interruptible/Curtailable loads and capacity market programs[J].Applied Energy.2010（87）：243-250.

[6]黄庆云.含分布式电源的配电网固定成本分摊[J].机电工程技术，2014（6）：182-185.

[7]田世明，王蓓蓓，张晶.智能电网条件下的需求响应关键技术[J].中国电机工程学报，2014，34（22）：3576-3589.

[8]王蓓蓓.面向智能电网的用户需求响应特性和能力研究综述[J].中国电机工程学报，2014，34（22）：3654-3663.

[9]黄燕燕，鹏春华.改进粒子群算法在电力系统经济调度中的应用[J].电力科学与工程，2011，27（4）：48-52.

[10]Chandrakand Rathore，Ranjit Roy.Impact of wind uncertainty，plug-in-electric vehicles and demand response program on transmission network expansion planning[J].Electrical Power and Energy Systems，2016（75）：59-73．

[11]Haoyong Chen，Zengyu Wang，Haifeng Yan，etal.Integrated Planning of Distribution Systems with Distributed Generation and Demand Side Response[J].Energy Procedia，2015（75）：981-986.

[12]颜伟，吕冰，赵霞，等.计及需求响应影响的配网可控DG 和开关协调规划[J].电网技术，2014，38（8）：2220-2224.

[13]储琳琳，张亮，倪群辉，等.当前电力体制下考虑需求侧管理的电网规划新思路[J].电力需求侧管理，2010，12（5）：9-13．

[14]赵波，王财胜，周金辉，等.主动配电网现状与未来发展[J].电力系统自动化，2014，38（18）：125-135.