太阳能热泵系统温度传感器测量的准确性校正

周 刚，杨永平

（陕西理工大学 陕西省工业自动化重点实验室，汉中 723000）

随着经济的发展，地球上的建筑面积也迅速增多，伴随而来的是建筑空调的耗能也迅猛增长，这使我国环境、能源背负着巨大的压力。对此，我国成功研制了太阳能热泵系统，它是用太阳能作为驱动能源，夏季可以为建筑供冷，冬季可以供暖，具有节能、环保的优点。但是，由于得不到准确的太阳能热泵系统最基本的温度参数，使得太阳能热泵系统的效率得不到有效的提高。

为了减小误差，我们可以确定一个校正方程对其数据进行处理。由于Cu50温度传感器具有电阻率高、测量精度高、反应快、成本低廉等优点，所以通常将Cu50温度传感器插入到换热管道内进行温度测量，由于换热管道的管径较小，导致传感器插入深度受限，影响了测量的准确度，所以必须对其进行R-T特性校正，常用方法有神经网络算法[1-2]，这种方法运算量大、速度慢，容易陷入局部极小而得不到全局最优值，精度也很低；硬件补偿算法[3-5]，这种方法结构复杂、操作繁琐、成本高、精度低，在实际工程应用中不能很好的应用；线性化法[6]，此种方法误差很大。为了保证数据的拟合精度和能够有效地查看拟合效果，通过最小二乘法将实测数据分成4段，利用Matlab对每段分别进行一次、二次、三次、四次拟合，这种拟合方法简单有效，通过拟合精度评估和在太阳能热泵系统的应用中验证了该方法测量精度很高。

1 Cu50温度传感器数据的标定

在众多Cu系列的热电阻中，Cu50热电阻测量精度很高，测量温度范围一般在-50～+150℃之间，依据太阳能热泵系统的实际温度范围，实验中选取10～100℃作为检测范围，利用高精度的数字温度计测量它的实际温度，通过恒温箱控制温度，依次改变箱里的温度进行检测，采用四线制接法对Cu50热电阻进行连接，用安捷伦表对Cu50热电阻随温度变化而对应的电阻值进行测量，可以得到电阻与温度之间的关系。图1所示为测量的实际数据。

图1 Cu50温度传感器R-T的实测数据的关系曲线Fig.1 Cu50 temperature sensors R-T relation curve of the actually measured data

由图1曲线可看出Cu50热电阻温度传感器具有非线性的特性，可以引出传统的校正方程，由文献[7]可知，Cu50热电阻温度传感器的温度和电阻关系（在-50～150℃）范围之间的校正方程为

式中：Rt为温度t时的电阻值；R0为t=0℃时的电阻值；A，B，C 分别为相应的系数，A=4.28×10-3℃-1，B=-9.31×10-8℃-2，C=1.23×109℃-3。 现将实测 R-T 数据分成（10～40 ℃）、（40～70 ℃）、（70～100 ℃）3 个区间，用最小二乘法对区间内数据分别进行一次、二次、三次、四次拟合，然后利用拟合精度评估原理得出Cu50温度传感器的最佳校正方程。

2 基于Matlab的数据拟合方法

2.1 最小二乘法拟合原理

写成矩阵形式为

解方程可得 a0，a1，a2，…，am。

2.2 基于Matlab的曲线拟合

利用 Matlab 中的内置函数 Polyfit（R，T，n）对Cu50热电阻温度传感器的实测R-T数据在（10～40℃），（40～70℃），（70～100℃） 区间内分别进行一次、二次、三次、四次拟合[10-12]，拟合以后的方程为

（1）一次拟合多项式

（2）二次拟合多项式

（3）三次拟合多项式

（4）四次拟合多项式

利用最小二乘法分段拟合后的图形如图2所示。

图2 最小二乘法的分段拟合图象Fig.2 Segmented fitting curve of least square method

2.3 拟合精度评估

为了评估校正方程的拟合精度，通常采用以下标准进行评估[13-14]：

（1）拟合残差

式中：E（f）为校正方程的拟合残差，E（f）越平稳，校正方程精度越高；yi为实测值；f（xi）为各拟合方程的拟合值。

（2）拟合偏差的最值

拟合偏差的最值就是拟合残差的最值，它包括最大拟合偏差Emax（f）和最小拟合偏差Emin（f）。拟合偏差最值越小，校正方程越理想。

（3）拟合残差的算术平均值

式中：Eave（f）为校正方程拟合残差的算术平均值，Eave（f）越小，校正方程精确度越高；n为实测数据点数。

（4）标准差

式中：Estd（f）为校正方程标准差，Estd（f）越小，校正方程精度越高。

2.4 评价校正方程

通过对各段拟合方程的系数进行误差分析得知，Cu50热电阻温度传感器分别在（10～40℃，40～70℃，70～100℃）区间内进行一次拟合时的误差震荡波动最大，二次、三次次之，四次拟合误差相对较小，所以可以通过对二次，三次，四次3种拟合的拟合偏差的最值、拟合残差的算术平均值及标准差进行对比，得到Cu50温度传感器的最佳校正方程，如表1所示。

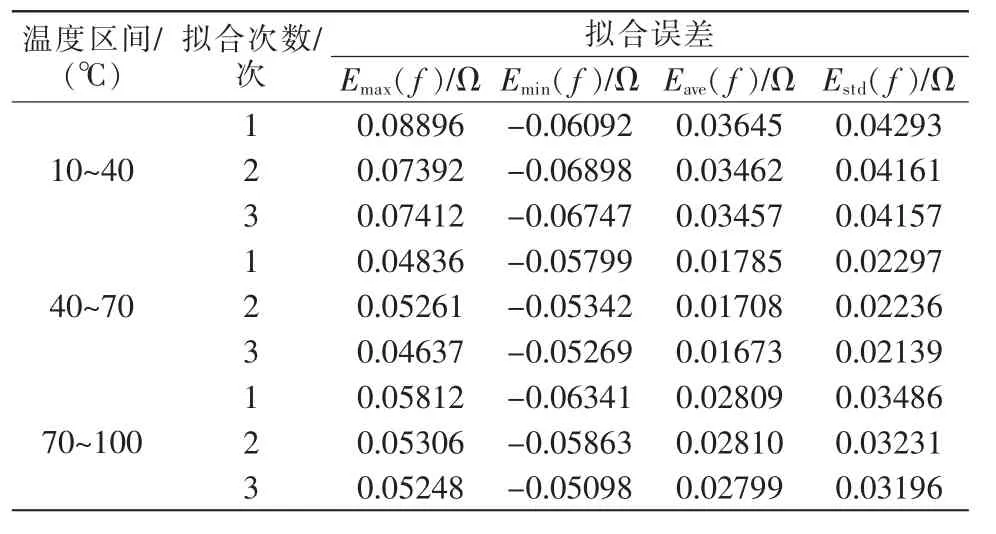
表1 Cu50温度传感器在10～100℃区间方程拟合误差Tab.1 Equation fitting error of Cu50 temperature sensor at 10～100 ℃

由表 1可以看出， 在 10～40℃，40～70℃，70～100℃区间上四次拟合方程的最大偏差、最小偏差、拟合残差的算数平均值、标准差最小、精度最高、逼近度最高。因此在10～100℃区间内，与Cu50热电阻温度传感器R-T的实测数据的精度最高的是四次拟合方程，校正方程为

3 结语

本文运用最小二乘法对Cu50热电阻温度传感器的实测数据进行分段拟合，得出了温度与电阻间的关系式，通过对拟合残差、拟合偏差的最值、拟合残差的算术平均值以及标准差的综合分析，得出在10～100℃范围内最适合Cu50热电阻温度传感器的校正方程是四次拟合方程，并经过实验检验得出校正方程比传统方程提高了2个数量级，并且在太阳能热泵系统中得到了广泛的应用。文中提出的校正拟合的方法，同样可用于其他类热电阻温度传感器的校正拟合。

[1]田丰，孙小平，赵昱，等.基于BP神经网络的浓度传感器非线性校正[J].计算机工程与应用，2005，41（3）：226-228.

[2]林康红，施惠昌，卢强，等.基于神经网络的传感器非线性误差校正[J].传感器技术，2002，21（2）：42-43，47.

[3]李颖.热电阻引线电阻补偿电路[J].中国计量，2003，8（9）：67-68.

[4]张修太，胡雪惠，翟亚芳，等.基于PT100的高精度温度采集系统设计与实验研究[J].传感技术学报，2010，23（6）：813-815.

[5]张志勇，辛长宇，朱玉龙，等.Pt100温度传感器非线性的补偿方法与电路实现[J].电子器件，2007，30（6）：2190-2191.

[6]严浩.应用柯西中值定理对控温仪表配热电阻进行线性化处理[J].环境技术，1999，17（3）：19-22.

[7]工业铂.铜热电阻JJG229-1998[S].北京：中国计量出版社，2004.

[8]陈岚峰，杨静瑜，崔崧，等.基于MATLAB的最小二乘曲线拟合仿真研究[J].计算机与现代化，2014，32（1）：75-78．

[9]杨大地，王开荣.数值分析[M].北京：科学出版社，2006：134-136.

[10]赵海滨.Matlab应用大全[M].北京：清华大学出版社，2012.

[11]唐家德.基于MATLAB的非线性曲线拟合[J].计算机与现代化，2008，26（5）：15-18.

[12]栗鹏飞，杨永平.太阳能制冷系统温度传感器测量的准确性研究[J].自动化与仪表，2014，29（3）：48-51，55.

[13]张鹏超，张强.一种NTC热敏电阻校正方程的试验研究[J].传感技术学报，2012，25（2）：221-223.

[14]钱政，王中宇，刘桂礼.测量误差分析与数据处理[M].北京：北京航空航天大学出版社，2008.