基于T-S模型的多变量非线性自适应预测函数控制

杨 宇，苏成利，施惠元，孙 柏

（辽宁石油化工大学 信息与控制工程学院，抚顺 113001）

近30多年来，预测控制[1]得到了广泛的关注，尤其是其第四代算法预测函数控制（PFC）[2-4]被很多学者研究。虽然预测函数控制因其良好的动态特性已被广泛地应用于实际生产当中。但当面对复杂的多变量非线性动态过程时，简单的预测函数控制很难满足实际需求。T-S模型是一种典型的动态系统模糊模型，各条模糊规则的结论均采用线性方程式的形式，使得线性控制策略对非线性系统控制得以很好的实现。因此，基于T-S模糊模型的预测控制研究已成为控制界研究的一大热点问题[5-7]。

文献[8]针对单变量非线性系统提出一种改进的自适应预测函数控制算法。该算法是基于T-S模糊模型来实现的，并结合在pH中和过程中的成功应用，验证了该算法的可行性。但是，该控制算法只适用于单变量系统，缺乏普遍性。文献[9]用T-S模糊模型对非线性系统进行逼近，从而得到线性模型。然后通过状态方程的形式直接计算控制律。该算法虽然避免求解Diophantine方程，但在实现过程中仍存在较大困难。

针对上述研究，并结合文献[8]所提出的单变量直接自适应模糊预测函数控制算法，本文把上述算法推广到多变量非线性系统中。该算法用辨识好的模糊规则，在每个采样时刻，分别对系统进行局部的动态线性化，从而得到了非线性系统的线性化模型。然后再通过直接迭代计算，分离当前时刻和以前时刻的系统输出、输入向量与之后时刻的系统输出、输入向量，从而得到模糊模型的预测输出。

本文以焦化加热炉中出口温度的控制TRC8103和TRC8105为例，对比文献[10]的控制算法，仿真结果表明本文所提的直接自适应模糊预测函数控制算法具有良好的跟踪性能和较强的抑制抗干扰能力。

1 非线性系统T-S模型问题描述

考虑如下具有n个输出、m个输入的MIMO非线性系统：

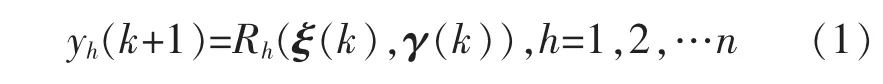
式中，nya和nub分别为系统第a个输出和第b个输入的阶次。

针对上文所描述的非线性动态过程，可用如下的T-S模糊模型来进行逼近和描述。那么，系统T-S模糊模型的第h个输出、第l条模糊规则Rhl，就可以表示为

如果 y1（k）是 μhl，1，…，y1（k-ny1）是 μhl，ny1，y2（k）是 μhl，ny1+1，…，y2（k-ny2）是 μhl，ny1+ny2，…，yn（k-nyn）是μhl，s，u1（k）是 δhl，1，…，u1（k-nu1）是 δhl，nu1，u2（k）是δhl，nu1+1，…，u2（k-nu2）是 δhl，nu1+nu2，…，um（k-num）是 δhl，t，

那么：

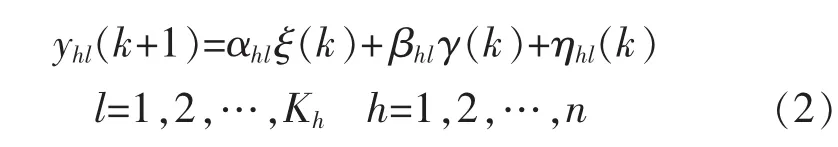
其中：Kh为第h个输出的模糊规则数；μhl为第h个输出、第 l条模糊规则的前件模糊子集；ηhl（k）为补 偿项；αhl， βhl为模糊模型后件参数向量；

系统（1）可看成是由像线性模糊模型（2）这样的多个子系统组成的，则所有模糊子系统输出的加权平均可组成系统（1）的输出，即：

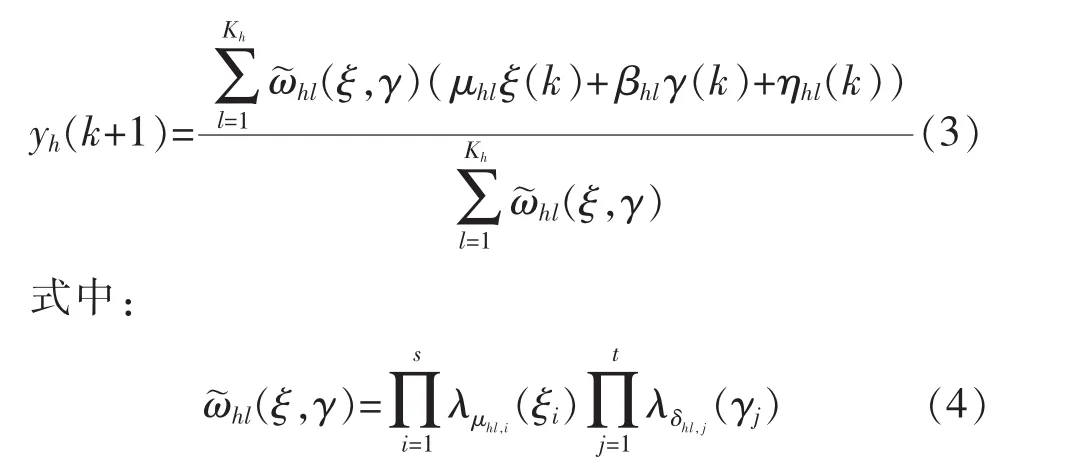
式中：λμhl（·）和 λδhl（·）为系统模糊规则模型前件变量的隶属度函数；Π是模糊算子，通常采用取小或乘积运算。

将式（5）代入式（3），则得到模糊模型的输出：

3 T-S模型在线辨识

为实现T-S模型后件参数的在线辨识，现设：

其中：Ψ（k-1）为系统的回归向量；Θ为未知后件参数向量。则式（7）可重新被写成如下形式：

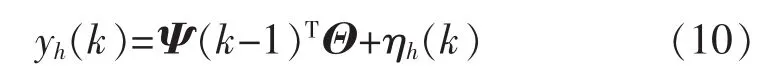
在对模型后件参数实行在线辨识运算时，本文选择用带遗忘因子最小二乘法来实行，具体的实行办法为

其中：ν为充分大的实数；ε为充分小的正实向量；I为适当维数的单位阵；矩阵 Pl（k-1），l=1，2，…，Kh为协方差矩阵 P（k-1）=［P1（k-1），…，PKh（k-1）］T的第 l个元素；l（k）=［yh（k）-Ψ（k-1）TΘ（k-1）］为模型输出预测误差；∂为遗忘因子，通常不小于0.9。

4 MIMO直接自适应模糊预测控制

将式（7）展开，可以得到过程的预测模型为

为了方便公式推导，在下文中，分别将 λha，p（k），ϑhb，q（k）记为 λha，p，ϑhb，q。则将式（14）代入式（13），式（13）可被写成：

由于η（k）是系统的不可测干扰，为了使推导过程更简便，在整个模型预测输出的推导计算过程中，假设 η（k）＝0。将式（15）作为过程的预测模型，为了计算简单式（15）可变换为

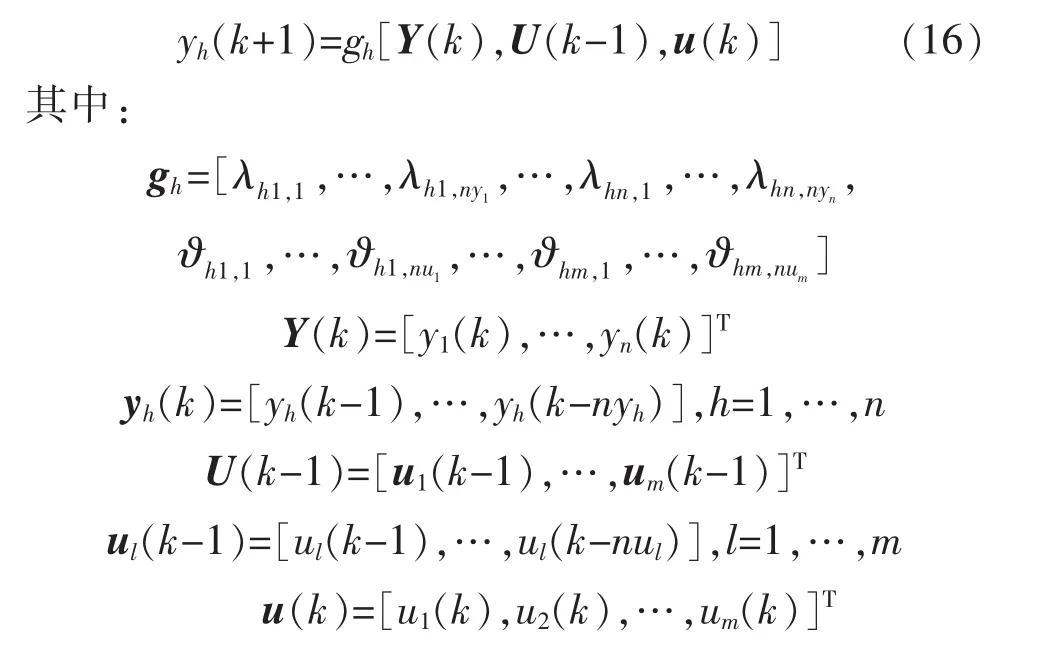
为了方便求取控制律，将当前时刻的输入单独提出计算，剩余则为过去时刻的输入和输出。则式（16）可变为

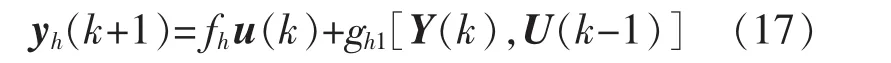
由于系统模型是通过阶跃响应测试方法获得，这里选取阶跃函数作为基函数。该基函数可表示为

其中，p为预测步长。根据式（16）和式（17）得预测 j步的输出：

为了克服在实际过程中模型失配、二次输入以及噪声干扰等影响，引入模型预测输出和实际过程输出偏差来校正预测输出，并且对未来时刻的偏差进行多项式拟合为

校正后的输出为

设参考轨迹为一阶指数形式：

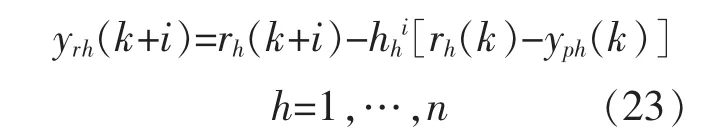
其中：yrh（k+i）为 k+i时刻系统第h 个输出的参考轨迹值；rh（k+i）为k+i时刻系统相应的设定值输入；yph（k）为k时刻第 h个过程输出；为采样周期；Trh为系统第h个输出的参考轨迹响应时间。

为了计算方便，将式（23）变为矩阵的形式为

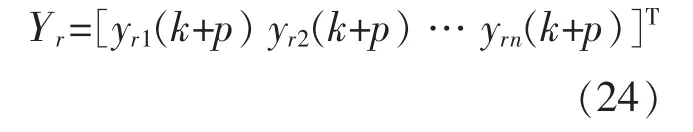
为了不失一般性，取最小方差的形式为目标函数：

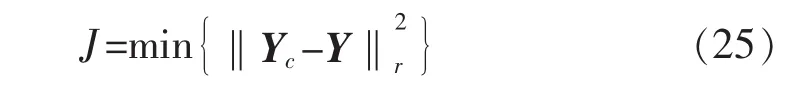
将式（22）和式（24）代入目标函数式（25）中，则可得使目标函数J最小的最优控制律为

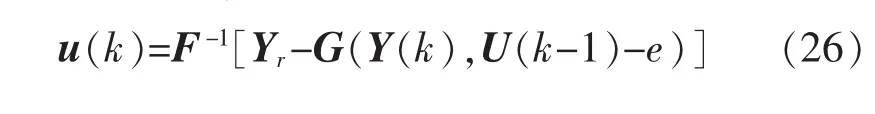
5 工业应用

5.1 焦化加热炉工艺流程

基本工艺流程如图1所示。焦化加热炉主要任务是对原料渣油、分馏塔底循环油迅速加热，为原油的进一步深加工提供原料。燃料主要是自产的高压瓦斯气，从南北两侧分别进入加热炉。原料渣油从南北两侧分两路送入加热炉对流室预热至330℃左右（南侧TR8152，北侧TR8153），之后合并进入分馏塔（T102）底，与焦炭塔（T101/5、6）顶来的油气接触并传热传质，原料中轻组分蒸发，上升至精馏段进行分离，生成富气、汽油、柴油、蜡油等产品，而原料中蜡油以上馏分与来自焦炭塔泵（P102/3）分两路送至加热炉辐射室迅速加热至495℃左右 （南侧TRC8103，北侧 TRC8105），之后进入焦炭塔（T101/5、6）进行裂解、缩合反应，生成石油焦碳。

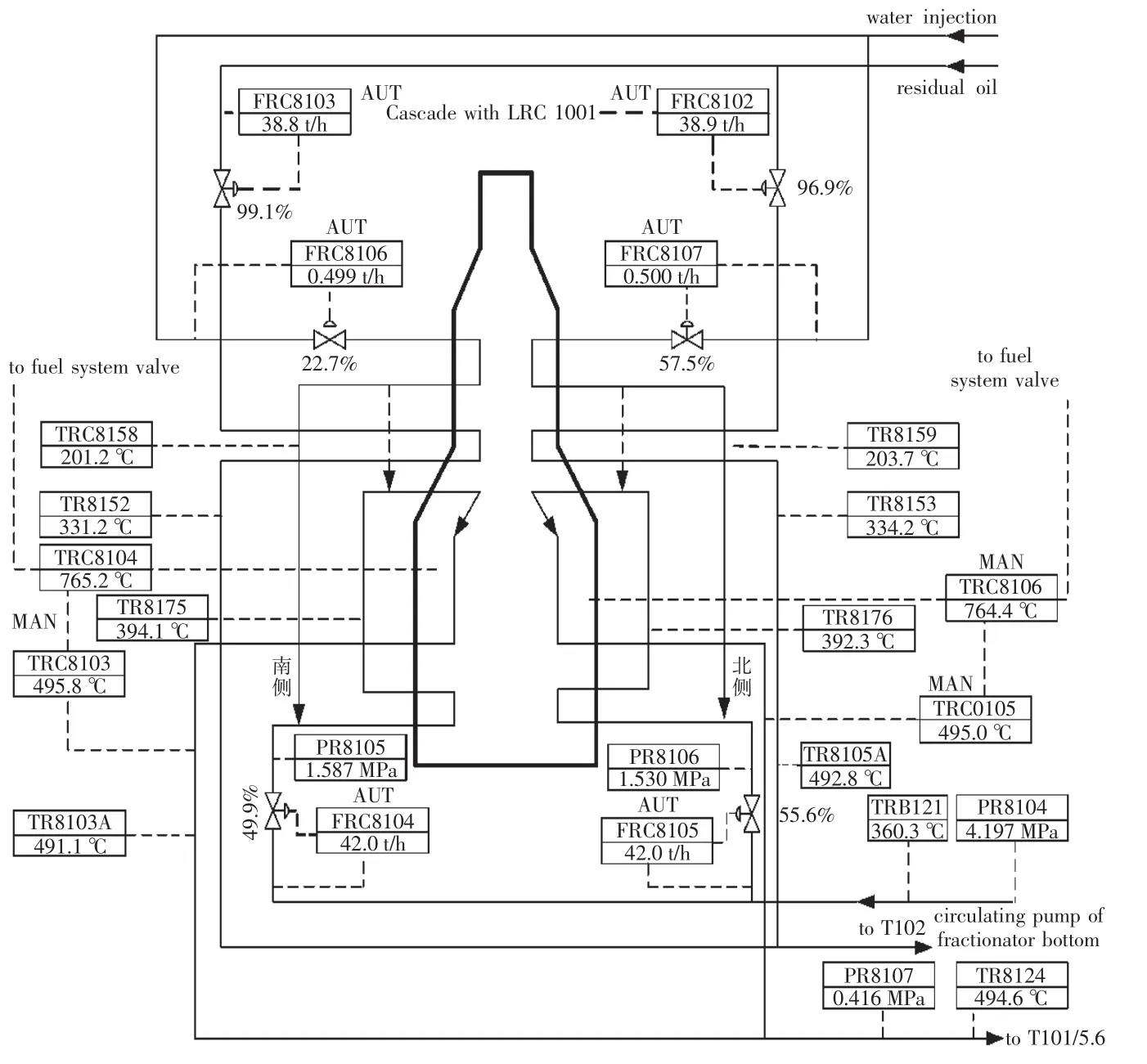
图1 焦化加热炉工艺流程Fig.1 Flow chart of coking furnace process

5.2 仿真验证

本文以焦化加热炉为例进行仿真验证，对其出口温度TRC8103和TRC8105进行控制。由于TRC8103出口温度的变化将会影响其出口温度TRC8105的变化，同样TRC8105出口温度的变化将会影响其出口温度TRC8103的变化，所以本文的控制是一个多变量控制。本文在原有的基础上进行改进，在外环加入本文所提的控制算法，内层采用PID控制作为控制层，可以抵抗外部的随机干扰，具有很好的抑制干扰的能力；外层是以内层PID闭环回路为广义对象的监督控制，外层提出的控制器的输出用来修正内层PID控制器的设定值。

T-S模型的前件模糊集合为高斯隶属度函数，其参数通过G-K聚类的方法获取。后件参数通过方程（8）获得。在辨识算法中，初始参数 Θ（0）＝0.002，P（0）＝1000I，其中 I为单位矩阵。 辨识的模型为

其中，高斯隶属度函数 Zi1，Zi2，Zi3，Zi4（i=1，2，3）如图2所示。

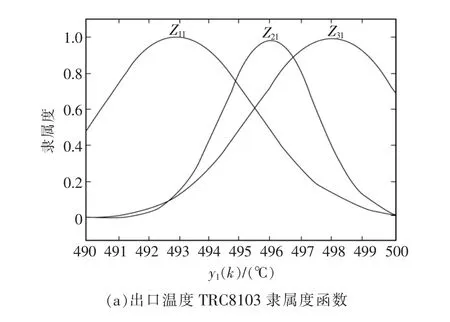
图2 隶属度函数Fig.2 Membership functions

控制器的参数为 ∂=0.96，p=35，Tr=0.8 s，Ts=1 s。在此采用本文提出的算法和文献[10]进行对比验证。对比结果如图3、图4所示。

通过图3和图4可以看出，对比文献[10]的控制算法，本文所提出的控制算法在设定值阶跃变化后具有更好的跟踪能力，控制更加平稳，并且控制量波动较小，具有良好的控制品质。

6 结语

本文针对多变量非线性系统，采用T-S模糊模型逼近系统模型，并且采用带遗忘因子的最小二乘辨识模型参数，将非线性问题转换为线性问题，使得计算量小、结构简单、控制效果更加明显，适合在工业现场应用。

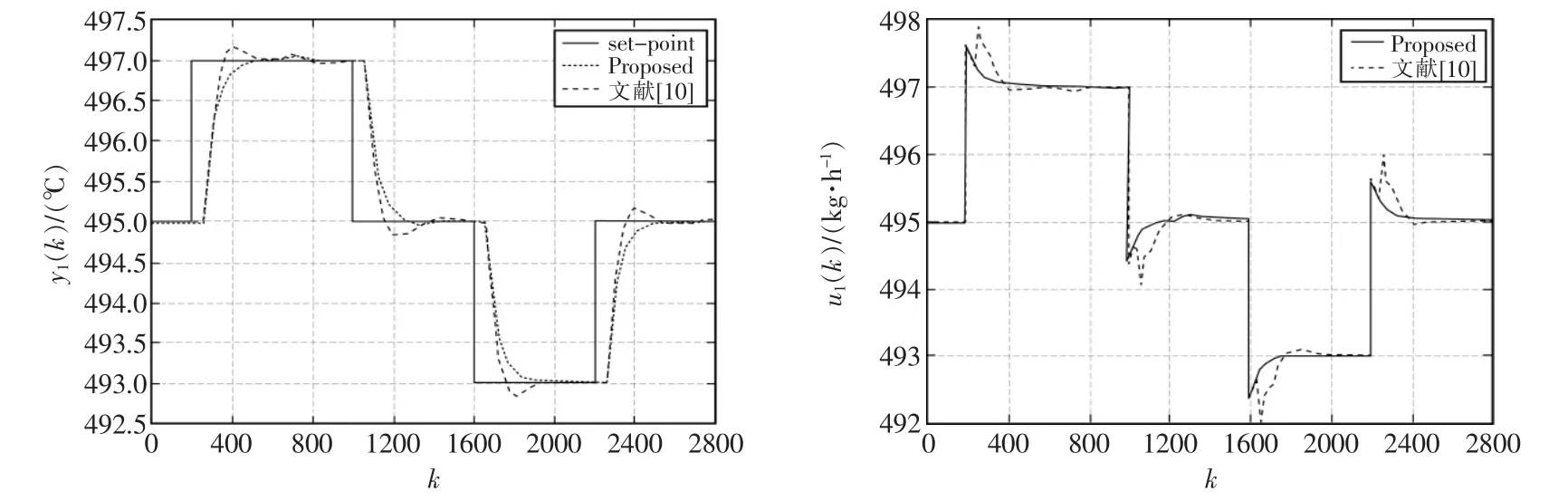
图3 出口温度TRC8103仿真结果Fig.3 Outlet temperature TRC8103simulation results

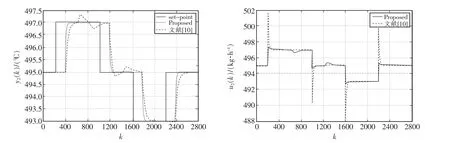
图4 出口温度TRC8105仿真结果Fig.4 Outlet temperature TRC8105 simulation results

[1]Clarke D W，Mohtadi C，Tuffs P S.Generalized predictive control[J].Automatica，1987，23（2）：137-160.

[2]Richalet J，et al.Predictive functional control-application to fast and accurate robots[C]//Pro of IFAC 10th World Congress.Munich，1987：251-258.

[3]张智焕，王树青，王宁.液压机器人的预测函数控制[J].控制与决策，2002，17（1）：120-122.

[4]Zhang R D，Li P，Xue A K，et al.A simplified iterative predictive functional control approach of chamber pressure of industrial coke furnace[J].Journal of Process Control，2010，20：464-471.

[5]Takagi T，Sugeno M.Fuzzy identification of systems and its applications to modeling and control[J].IEEE Transcations on Systems，Man，and Cybertnetics，1985（15）：116-132.

[6]邢宗义，胡维礼，贾利民.基于T-S模型的模糊预测控制研究[J].控制与决策，2005，20（5）：495-499.

[7]师五喜.未知多变量非线性系统自适应模糊预测控制[J].控制理论与应用，2011，28（10）：1399-1404.

[8]苏成利，李平，邓淑贤，等.一种基于T-S模糊模型的自适应预测函数控制[J].控制工程，2007，14（6）：610-613.

[9]Simon Oblak，Igor Skrjanc.Multivariable fuzzy predictive functional control of a MIMO nonlinear system[C]//In：Proceedings of the 2005 IEEE，International Symposium on Intelligent Control，Limassol，Cyprus，2005：27-29.

[10]Su C L，Li P.Adaptive predictive functional control based on Takagi-Sugeno model and its application to pH process[J].Journal of Central South University of Technology，2010 （2）：363-371. ■