多种颤振模态参数辨识方法对比研究

王绍楠 卢晓东 寇宝智

摘 要：介绍了颤振试飞中三种比较经典的频域模态参数辨识方法，分别是有理分式正交多项式法、最小二乘复频率法、频域子空间法。通过仿真算例研究了这三种方法对不同程度噪声下扫频响应数据的模态参数辨识效果。将其应用于真实试飞数据中，得到三种方法计算的典型模态频率及阻尼随速度的变化曲线。研究显示，有理分式正交多项式法在处理信噪比低、模态密集的数据时更加准确鲁棒。

关键词：颤振试飞；模态参数辨识；有理分式正交多项式；最小二乘复频率；频域子空间

中图分类号：V217 文献标志码：A 文章编号：2095-2945（2018）34-0005-03

Abstract： This paper introduces three classical identification methods of modal parameters in frequency domain in flutter flight test， which are rational fraction orthogonal polynomial method， least square complex frequency method and frequency domain subspace method. The effects of these three methods on modal parameter identification of swept frequency response data under different degrees of noise are studied by simulation examples. It is applied to the real flight test data， and the typical modal frequency and damping versus velocity curves calculated by three methods are obtained. The research shows that the rational fraction orthogonal polynomial method is more accurate and robust when dealing with the data with low signal-to-noise ratio and high modal density.

Keywords： flutter flight test； modal parameter identification； rational fraction orthogonal polynomial； least square complex frequency； frequency domain subspace

顫振试飞是世界公认的一类风险试飞科目，一直广受重视。其目的是为了获得飞机的颤振特性，包括模态参数（频率和阻尼），颤振类型以及颤振边界。

目前最常用的试飞方法是在飞行包线上选取若干高度，在每个高度上选取几个速度点进行稳定平飞，其间对飞机结构进行激励，获得飞机结构响应信号。然后，通过数据处理辨识出不同结构模态的频率和阻尼；最终，得到模态频率和阻尼随速度的变化曲线，通过阻尼外推得到颤振临界速度[1]。可见，模态参数的准确辨识是得到正确颤振速度的前提。

近几十年来，研究人员提出并发展了众多模态参数辨识方法。从辨识信号的特征考虑，可以分为频域、时域法和时频域法[2]。由于时域法和时频域法在计算速度上不能很好的满足颤振试飞的需要，故目前国内颤振试飞最主要采用的还是频域方法。其中，有理分式正交多项式法[3]在实际颤振试飞中应用最多。而随着模态辨识技术的发展，其他模态辨识方法如最小二乘复频率法[4]及频域子空间方法[5]在颤振试飞中得到应用。但目前并未有将这些方法应用信噪比低、模态密集的真实试飞数据来研究其对噪声敏感度及密集模态识别能力的相关报导。故本文通过仿真算例和扫频激励下的实际颤振试飞数据，进一步研究了这三种方法对模态参数的识别效果与稳定性，具有较大工程指导意义与实用价值。

1 模态参数辨识方法

1.1 有理分式正交多项式法（RFOP）

频响函数模型表示为有理分数的形式：

引入理论模型与实测值直接的误差，并使误差对系数ak、bk线性化。通过误差最小化的思路，以正交多项式分别对分子、分母进行曲线拟合。令分母多项式为零，可以得到极点？姿r，最终可求得固有频率和阻尼比：

1.2 最小二乘复频率法（LSCF）

最小二乘复频率法的出发点是频响函数的标量矩阵分式：

1.3 频域子空间法（SUBS）

多输入多输出系统可用离散时间状态空间模型来描述：

2 仿真算例

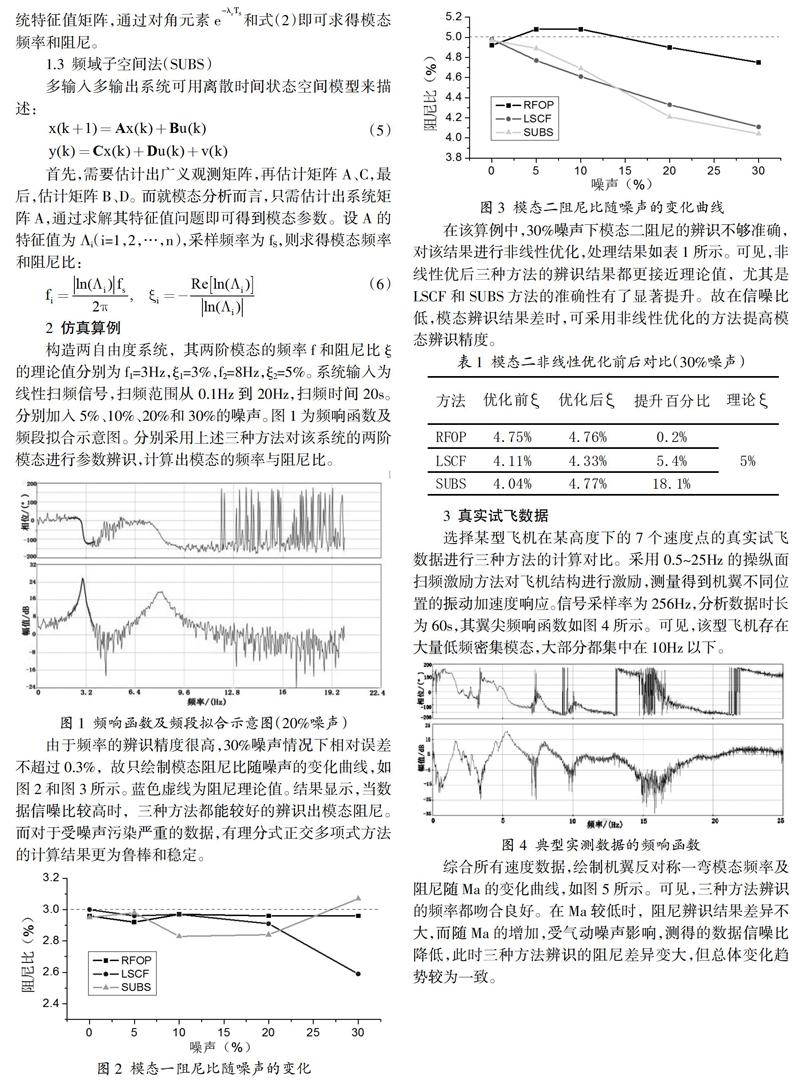
由于频率的辨识精度很高，30%噪声情况下相对误差不超过0.3%，故只绘制模态阻尼比随噪声的变化曲线，如图2和图3所示。蓝色虚线为阻尼理论值。结果显示，当数据信噪比较高时，三种方法都能较好的辨识出模态阻尼。而对于受噪声污染严重的数据，有理分式正交多项式方法的计算结果更为鲁棒和稳定。

在该算例中，30%噪声下模态二阻尼的辨识不够准确，对该结果进行非线性优化，处理结果如表1所示。可见，非线性优后三种方法的辨识结果都更接近理论值，尤其是LSCF和SUBS方法的准确性有了显著提升。故在信噪比低，模态辨识结果差时，可采用非线性优化的方法提高模态辨识精度。

3 真实试飞数据

选择某型飞机在某高度下的7个速度点的真实试飞数据进行三种方法的计算对比。采用0.5～25Hz的操纵面扫频激励方法对飞机结构进行激励，测量得到机翼不同位置的振动加速度响应。信号采样率为256Hz，分析数据时长为60s，其翼尖频响函数如图4所示。可见，该型飞机存在大量低频密集模态，大部分都集中在10Hz以下。

综合所有速度数据，绘制机翼反对称一弯模态频率及阻尼随Ma的变化曲线，如图5所示。可见，三种方法辨识的频率都吻合良好。在Ma较低时，阻尼辨识结果差异不大，而随Ma的增加，受气动噪声影响，测得的数据信噪比降低，此时三种方法辨识的阻尼差异变大，但总体变化趋势较为一致。

分别对各自的结果进行非线性优化。以某高度某Ma的数据为例，展示了机翼反对称一弯的模态结果，如表2所示。可看出优化前阻尼差异较大，优化后三种方法辨识的阻尼基本一致。将其各自优化后的结果作为基准，计算出误差。能明显看出，RFOP方法相比另外两种方法阻尼误差更小，在处理信噪比低的试飞数据时更有优势。

4 结论

有理分式正交多项式相比于最小二乘复频率和频域子空间方法，更适宜处理工程中信噪比低且模态密集的试飞数据。非线性优化方法可在一定程度上提升阻尼识别精度。

参考文献：

[1]张伟伟，钟华寿，肖华，等.颤振飞行试验的边界预测方法回顾与展望[J].航空学报，2015，36（5）：1367-1384.

[2]卢晓东.大型飞机颤振试飞低频密集模态参数辨识[J].飞行力学，2014，32（3）：270-272.

[3]王彤，张令弥.有理分式正交多项式频响函数模态参数识别[J].航空学报，2003，24（2）：140-143.

[4]Guillaume P.，Verboven P.，et al. A poly-reference implementation of the least-squares complex frequency-domain estimator[C]. Proceedings of IMAC 21， Kis-simmee， FL， USA， Feb. 2003.

[5]唐炜，史忠科.飞机颤振模态参数的频域子空间辨识[J].航空学报，2007，28（5）：1175-1180.