福建省主要大气污染物分布研究
白春妹, 赖焕生
(1. 福州大学土木工程学院, 福建 福州 350116; 2. 福州大学石油化工学院, 福建 福州 350116)
0 引言
大气颗粒物质(particle matter,PM)是大气中存在的各种固态和液态颗粒状物质的总称. PM2.5和PM10分别是指空气动力学直径小于或者等于2.5和10 μm的大气悬浮颗粒物. PM2.5因其粒径小、比表面积大且经常含有重金属等有毒物质,可通过肺泡壁进入毛细血管,再进入整个血液循环系统,对人体的呼吸系统和心血管系统造成伤害. 研究发现,PM2.5质量浓度每升高10 mg·m-3,呼吸系统疾病日死亡率将上升1%,心脑血管疾病日死亡率将上升0.5%[1-4]. PM10会引起哮喘等呼吸系统疾病,增加心脏病的患病率和死亡率,并具有潜在的致癌性. PM2.5和PM10主要来源于煤炭发电、工业生产和汽车尾气的排放,是导致我国工业化进程中备受关注的雾霾天气的“罪魁祸首”. 而且,PM的出现降低了大气能见度,易引发交通事故. 因此,有关PM浓度及其分布仍然是研究的热点,尤其像在中国这样的发展中国家.
除了PM2.5和PM10,大气环境质量还受SO2、NO2、CO和O3等污染物的综合影响. 其中,SO2、NO2和CO对健康的危害包括加重心脑血管疾病,引起呼吸系统疾病和肺发炎; 而O3会加重慢性呼吸系统疾病并引起短期内肺功能的下降[5-7]. SO2主要来自煤、石油等燃料的燃烧,及硫酸厂排放的废气等; NO2主要来源于机动车排放的废气和燃放烟花爆竹; CO主要来源于化石燃料的不完全燃烧和汽车的尾气等. 实验研究表明,SO2、NO2和CO等大气污染物会通过大气化学反应生成PM,尤其在空气湿度较大的雾霾天气下[8]. O3污染物指近地面大气层中超过一定含量并对人体产生危害的一种环境污染物,但不包括平流层中的O3. 目前,O3已成为我国大部分地区夏秋季的主要污染物,为此新的环境空气质量标准将O3纳入常规检测指标[9-10]. O3污染主要来自汽车尾气、石油化工行业、火电厂等产生的挥发性有机物、氮氧化物、一氧化碳等物质经过光化学反应生成的二次污染物. 依照氮守恒定律,氮氧化物之类的大气污染物一般折算成NO2来核算大气环境质量标准.
在我国,已有一些研究工作致力于探索气候变化(如沙尘暴)中的PM和主要大气污染物浓度的动态变化过程[11-14]; 有些是侧重于研究大城市中的PM2.5的化学组分等[15-16]. 然而,目前还没有针对福建省的关于PM2.5、PM10、SO2、NO2、CO和O3等大气污染物浓度分布情况的全面研究,也没有能用于量化这些主要大气污染物浓度分布关系的模型. 另外,大气中PM浓度的分布受很多因素的影响,如:气候因素、地表植被覆盖、土地利用类型、天气、风向和湿度等[17]. 各个城市因所主导的因素的不同会引起PM呈现不同的分布特征和周期变化.
以福建全省九市(福州、厦门、泉州、漳州、南平、三明、龙岩、宁德和莆田)为研究对象,应用皮尔逊相关系数表征这些大气污染物之间的相关关系,以便全面了解福建省主要大气污染物的分布特征和相关关系. 采用因子分析法的多变量统计分析方法[18],将这些主要大气污染物的错综复杂关系进行处理,以提取综合影响因子. 因子分析法应用大气污染物领域最早见于Blifford等应用因子分析法对美国30多个城市的气溶胶来源的解析[19]. 王明星[20]运用因子分析法对北京气溶胶污染物的来源进行研究; 因子分析法在戴昭华[21]、胡伟等[22]的研究中也得到运用.
1 数据来源与分析方法
1.1 数据来源
从“中国环境监测总站的数据库”官方网站上采集获得福建全省九市(福州、厦门、泉州、漳州、南平、三明、龙岩、宁德和莆田)2015年的PM2.5、PM10、SO2、NO2、CO和O3等大气污染物的每日质量浓度值.
1.2 分析方法
采用因子分析法对所采集的大量数据进行处理、掘取数据信息,从而用较少的有代表性的因子来说明多个大气污染物变量所含有的主要信息. 因子分析法是一种多变量统计研究方法,它的基本思想是将观测变量进行分类,将相关性高的或者联系比较紧密的分在同一类中,从一系列错综复杂又相互紧密联系的变量出发,提取出几个能够全面反映所选变量的综合因子,又称公共因子. 因子分析法就是寻找这些公共因子的模型分析法,它是在主成分的基础上构筑若干意义较为明确的公因子,以它们为框架分解原变量,以此考察原变量间的联系与区别. 因子分析法是主成分分析法(principal component analysis, PCA)[23]的推广和深化,也是一种把多个变量化为少数几个综合变量的多变量分析方法,目的是用少数几个不可观测的隐变量来解释原始变量之间的相关关系.
在因子分析模型中[23],每个变量表示为m个共同因子的线性组合. 因子分析法模型描述成如下矩阵形式:
式中:X是p个原观测变量所组成的向量;μ是X的均值组成的向量;F称为X的公共因子或潜因子,且彼此正交;L称为因子载荷矩阵,表示观测变量X和相应因子F之间的相关系数;ε是特殊因子矩阵. 具体来说,Lpm表示Xp变量对第m个因子Fm的负荷,或者说是原变量与公共因子的相关程度.Lpm越大,表明Xp与Fm之间的相依程度越大,或者公共因子Fm对于Xp的载荷量越大. 建立因子分析模型的目的不仅是找出主因子,更重要的是预测关键主因子的意义,以便对实际问题进行分析. 如果一开始求出的主因子代表的意义不是很突出,还需要进行因子旋转,通过适当的旋转得到比较满意的主因子. 最常用的旋转方法是最大方差正交旋转法[23]. 因子旋转的目的是使因子载荷矩阵中因子载荷的平方值向0和1两个方向分化,使大的载荷更大,小的载荷更小. 运用因子分析法有以下几个步骤:首先确认原变量是否适合做因子分析; 其次构造因子变量; 再者是利用旋转方法(如果需要的话)使因子变量更具有可解释性; 最后是计算因子变量得分. 其中,在判断原变量是否适合做因子分析中,首先需要计算得到原变量之间的相关系数,确保至少一对变量之间显著性相关,并且至少一对变量之间显著性不相关. 一方面,至少一对原变量之间显著性相关,才能运用因子分析法提取公共因子; 另一方面,至少一对变量之间显著性不相关,才有必要对原数据变量进行因子分解.
2 结果与讨论
2.1 原始监测数据的相关系数矩阵R
首先应用主成分分析法思想对福建全省2015年九市监测得到的主要大气污染物浓度进行因子分析,用皮尔逊相关系数法表征PM2.5、PM10、SO2、NO2、CO和O3浓度之间的相关关系,见表1. 由监测数据计算得到的相关系数矩阵R可知PM2.5和PM10相关系数为0.889 05,且显著性水平小于0.000 1. 若显著性水平标准设为0.1的情况下,PM2.5和PM10之间高度相关,且此相关性不可被忽略. 另一方面,NO2和O3之间的相关系数为-0.013 87,且显著性水平为0.427 2(大于0.1的显著性水平标准),意味着NO2和O3之间的相关性系数比较小,并且可以被忽略. 由表1中大气污染物之间的相关系数可总结得出,在显著性水平标准为0.1的情况下,除了NO2和O3浓度显著性不相关之外,其余的污染物浓度如PM2.5和PM10、PM2.5和SO2、PM2.5和CO、PM10和SO2、PM10和CO等均具有显著性相关关系. 运用因子分析法的前提是,原有数据变量之间至少有一对显著性相关,以及至少有一对变量之间显著性不相关. 因此,该研究的原始数据变量适合运用因子分析法进行公共因子分解.
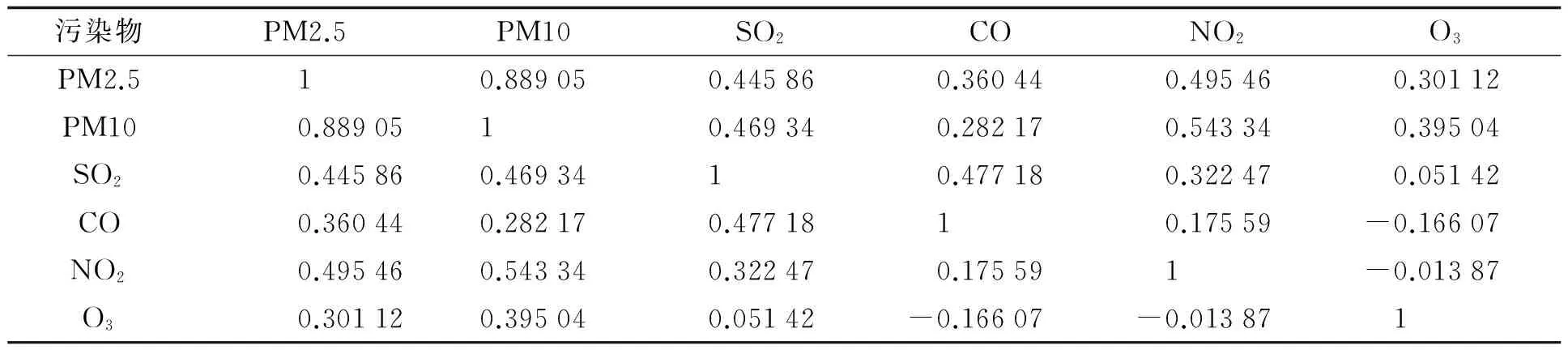
表1 皮尔逊相关系数矩阵R
2.2 福建省主要大气污染物的主因子分析
以福建全省九市监测到的每日PM2.5、PM10、SO2、NO2、CO和O3质量浓度值(总共3 280个数据,其中福州市有360个观测值,其余各有365个观测值)为原始数据,运用因子分析法进行分析. 结果显示,2015年全省范围内,PM2.5、PM10、SO2、CO、NO2、O3平均质量浓度值分别为28.737、49.472、10.866、0.832、23.852、83.962 μg·m-3. 运用PCA思想对相关系数R进行因子分析,计算得其特征值和特征向量,特征值的计算结果见表2. 表2显示:第1个公共因子(或称第一个主成分)对数据方差具有最大贡献率,可以解释48.42%的数据方差; 第2个公共因子对数据方差的贡献率为21.52%. 按照惯例,特征值大于1的公共因子将选取为主要的公共因子. 因此,该研究选取了第1个和第2个公共因子为主因子. 综合来看,第1、2个公共因子合起来总共可以解释69.94%的数据方差,该结果也可以用特征值按下面的方程计算得到 (λ1+λ2)/p≈69.94%. 图1表示的是相关系数的特征值和其因子所解释的数据方差和累计数据方差. 由图1可知,两个主因子对应的特征值均大于1,二者合起来可以解释大约70%的数据方差.

表2 R的特征值
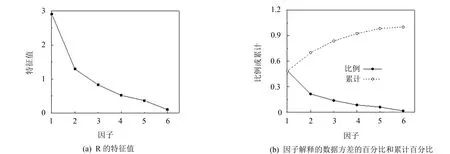
图1 R的因子分析结果 Fig.1 Factor analysis results for R

污染物第1个主因子第2个主因子PM2.50.902610.15562PM100.915380.25302SO20.68430-0.34836CO0.51199-0.64319NO20.65664-0.07567O30.301480.81364
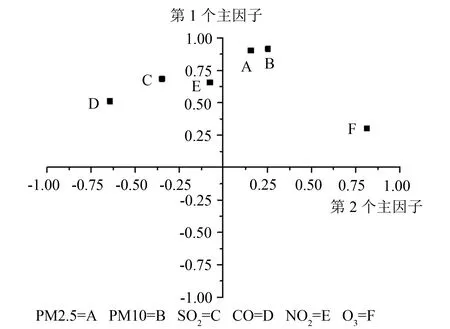
图2 主因子模式图Fig.2 Plot of factor pattern for Factor 1 and Factor 2
计算得到的相关系数R的主因子载荷矩阵L,见表3,对于第1个主因子,各个原变量PM2.5、PM10、SO2、NO2、CO和O3的载荷量分别为0.902 61、0.915 38、0.684 30、0.511 99、0.656 64和0.301 48. 即六类大气污染物质量浓度变量都与第1个主因子有相关性,其中PM10与第1个主因子的相关系数最大,其后依次为PM2.5、SO2、NO2、CO和O3与第1个主因子的相关系数. 而对于第2个主因子,O3与第2个主因子的相关系数最大为0.813 64,CO与第2个主因子的相关系数次之,相比较而言,第2个主因子对于PM2.5、PM10、SO2、NO2的载荷量较小. (此处,若采用最大方差正交旋转法旋转得到的主因子模式并未使因子载荷矩阵的平方值更好地向0和1两方向分化,也就是说采用主成分分析法分解的主因子已经使因子载荷分化得还可以,而不需要再进行旋转). 显然,若根据第1个主因子得分大小程度来对这六类大气污染物的污染严重程度进行排序的话,PM10污染最严重,然后依次是PM2.5、SO2、NO2、CO和O3. 运用因子分析法分解的第1个主因子更多的包含了PM2.5、PM10、SO2和NO2的污染影响,而第2个主因子更多包含O3的质量浓度影响. 为了更直观地理解,图2是进行因子分解后的六类大气污染物的模式分布图. 从图2也可看出,字母A、B、C、E代表的PM2.5、PM10、SO2和NO2更偏向于分布在第1个主因子的轴线上,而字母F代表的O3更多的分布在靠近第2个主因子的轴线上. 字母D代表的CO则分布在介于第1个主因子和第2个主因子之间,但更偏向于第2个主因子. 按照来源来说,PM2.5和PM10主要来源于地面粉尘、燃煤排放的烟尘等; SO2主要来源于煤、石油等燃料的燃烧,及硫酸厂排放的废气等; CO主要来源于化石燃料的不完全燃烧和汽车的尾气等; NO2主要来源于机动车排放的废气和燃放烟花爆竹; O3主要来源于汽车尾气、石油化工行业、火电厂等产生的氮氧化物和挥发性有机物等的光化学反应形成的二次污染. 另外,大气污染物之间存在一定的转化关系,当空气湿度较大时SO2、NO2和CO等大气污染物会通过大气化学反应生成PM. 结合大气污染物的来源和意义,本研究运用因子分析法得到的第1个主因子更多体现的是大气中PM2.5、PM10、SO2等原生污染物(或称一次污染物)的综合,第2个主因子更多体现的是O3之类的二次污染物. 从地域上看,各个城市均呈现PM10质量浓度值比PM2.5高的情况,即PM10的污染程度比PM2.5严重. 其中,大气颗粒物质PM2.5和PM10污染最严重的城市是漳州市,其平均质量浓度值分别为56.423和33.633 μg·m-3,分别比全省均值高了6.951和4.896 μg·m-3. 大气污染物SO2和CO污染最严重的城市是三明市,其平均质量浓度值分别为18.986 μg·m-3和1.277 mg·m-3,分别高于全省的均值(10.866 μg·m-3和0.832 mg·m-3). 大气污染物NO2污染最严重的城市是福州市,比全省平均水平(23.852 μg·m-3)高了7.001 μg·m-3. O3污染最严重的是泉州市,全年平均水平为96.740 μg·m-3,比全省平均质量浓度值高了12.778 μg·m-3. 运用因子分析法对各个地级市的大气污染物分别进行因子解析,各个城市的因子分析结果均显示第1个主因子与PM和SO2等原生大气污染物的相关关系最大,而与O3的相关性最小,而第2个主因子对于O3的载荷量最大. 由此可见,各个城市因子分析结果与全省范围内的综合因子分析结果一致,所分解生成的第1个主因子均反映PM和SO2等的原生大气污染物,第2个主因子则主要反映O3之类的二次大气污染物.
最后,本研究工作是基于福建省当前大气环境污染状况进行的. 虽然整体上福建省的大气环境优于京津冀等北方地区,但是也需要提早防范可能产生的严重大气污染问题. 另外,在未来的研究工作中,将进一步采集更多的大气污染物数据,运用时间序列分析法建立相应的大气污染物时间序列分析模型,以预测未来福建省大气污染物趋势.
3 结语
1) 六类大气污染物中,污染最严重的是PM10,然后依次是PM2.5、SO2、NO2、CO和O3.
2) 在统计显著性水平标准为0.1的情况下,除了NO2和O3显著性不相关之外,其余大气污染物之间均存在显著性相关关系,这些相关关系的数据也进一步印证了PM和SO2、NO2、CO之间存在相互转化的事实. 其中,PM2.5和PM10之间相关系数最大为(0.889 1),PM10和NO2之间的相关系数次之为(0.543 3).
3) 从全省范围内的大气污染物质量浓度因子分析结果可以明显看出, 原生大气污染物PM和SO2等聚类在一起形成第1个主因子,而O3之类的二次大气污染物则归类成第2个主因子. 在第1个主因子中,大气颗粒物质的影响依旧是最大的,这也印证了在中国目前的大气环境问题中,PM10和PM2.5正逐渐成为人们关注的热点污染问题.
[1] ZHOU Y, FU J S, ZHUANG G,etal. Risk-based prioritization among air pollution control strategies in the Yangtze River Delta, China[J]. Environ Health Persp, 2010, 118(9): 1 204-1 209.
[2] CHEN C, ZHAO B. Review of relationship between indoor and outdoor particles: I/O ratio, infiltration factor and penetration factor[J]. Atmos Environ, 2011, 45(2): 275-288.
[3] LANGRISH J P, LI X, WANG S,etal. Reducing personal exposure to particulate air pollution improves cardiovascular health in patients with coronary heart disease[J]. Environ Health Persp, 2012, 120(3): 367-372.
[4] CHU M, SUN C, CHEN W,etal. Personal exposure to PM2. 5, genetic variants and DNA damage: a multi-center population-based study in Chinese[J]. Toxicol Lett, 2015, 235(3): 172-178.
[5] BERNARD S M, SAMET J M, GRAMBSCH A,etal. The potential impacts of climate variability and change on air pollution-related health effects in the United States[J]. Environ Health Persp, 2001, 109: 199-209.
[6] CHEN C, ZHAO B, WESCHLER C J. Assessing the influence of indoor exposure to “outdoor ozone” on the relationship between ozone and short-term mortality in US communities[J]. Environ Health Persp, 2012, 120(2): 235-240.
[7] CHEN C, ZHAO B, WESCHLER C J. Indoor exposure to “outdoor PM10”: assessing its influence on the relationship between PM10 and short-term mortality in US cities[J]. Epidemiology, 2012, 23(6): 870-878.
[8] CHAN C K, YAO X. Air pollution in mega cities in China[J]. Atmos Environ, 2008, 42(1): 1-42.
[9] 黄亮. 我国臭氧污染特征及现状分析[J]. 环境保护与循环经济,2014,34(5):64-66.
[10] 罗雄标. 臭氧污染物来源与控制[J]. 资源节约与环保,2015,8:137.
[11] CHENG T, LU D, WANG G,etal. Chemical characteristics of Asian dust aerosol from Hunshan Dake Sandland in northern China[J]. Atmos Environ, 2005, 39(16): 2 903-2 911.
[12] XIE S, TONG Y, ZHANG Y,etal. Characteristics of PM10, SO2, NOxand O3in ambient air during the dust storm period in Beijing[J]. Sci Total Environ, 2005, 345(1): 153-164.
[13] CHOI Y, HO C, CHEN D,etal. Spectral analysis of weekly variation in PM10 mass concentration and meteorological conditions over China[J]. Atmos Environ, 2008, 42(4): 655-666.
[14] FAN Q, SHEN C, WANG X,etal. Impact of a dust storm on characteristics of particle matter (PM) in Guangzhou, China[J]. Asia-Pac J Atmos Sci, 2013, 49(1): 121-131.
[15] YANG F, TAN J, ZHAO Q,etal. Characteristics of PM 2.5 speciation in representative megacities and across China[J]. Atmos Chem Phys, 2011, 11(11): 5 207- 5 219.
[16] ZHANG F, XU L, CHEN J,etal. Chemical characteristics of PM 2.5 during haze episodes in the urban of Fuzhou, China[J]. Particuology, 2013, 11(3): 264-272.
[17] HAO Y, LIU Y. The influential factors of urban PM 2.5 concentrations in China: a spatial econometric analysis[J]. J Clean Prod, 2016, 112: 1 443-1 453.
[19] BLIFFORD I H, MEEKER G O. A factor analysis model of large scale pollution[J]. Atmos Environ, 1967, 1(2): 147-157.
[20] 王明星. 用因子分析法研究大气气溶胶的来源[J]. 大气科学,1985,9(1):73-81.
[21] 戴昭华. 统计数学在环境科学中的应用[J]. 环境科学丛刊,1987,1:1-44.
[22] 胡伟,魏复盛. 中国4城市空气颗粒物元素的因子分析[J]. 中国环境监测,2003,19(3):39-41.
[23] JOHNSON R A, WICHERN D W. Applied multivariate statistical analysis[M]. 4th ed. New Jersey: Prentice Hall, 1998.

