碳纤维增强复合材料正交切削加工性能数值分析
林有希,陈德雄,任志英,林 华
(福州大学机械工程及自动化学院,福建 福州 350116)
0 引言
碳纤维增强复合材料 (carbon fiber reinforced polymer,CFRP)由于其良好的机械性能和物理性能被广泛运用于航空、军事、汽车等多个工业领域[1]. 然而,碳纤维复合材料在微观上呈现纤维、树脂以及界面组成的混合态,在切削加工过程中容易导致纤维基体脱粘、基体开裂等缺陷,严重影响工件的切削加工质量和使用性能[2]. 目前学者较多采用实验方法对CFRP的切削加工性能进行研究. 然而,CFRP的实验研究需要耗费大量人工及材料成本,并且CFRP的切屑多为粉末状,吸入对人体有一定的伤害[3], 因此,采用有限元仿真方法对CFRP的切削过程进行研究具有一定的优势.
Arola和Ramulu[3]通过预定义断裂面研究材料的去除过程,切屑形成过程包括初始和二次断裂两个过程. Ramesh等[4]根据弹塑性理论和完全拉格朗日方程模拟研究FRPs的切削过程. Lasri等[5]采用刚度退化理论研究切削力和损伤失效模式,例如基体破坏、纤维基体脱粘和纤维断裂等. Mahdi和Zhang[6]采用准静态方法模拟研究纤维方向与切削力之间的关系,所得模拟结果与相关实验研究成果相吻合. 路冬等[7]研究0°和90°纤维方向的基体开裂和压溃损伤,分析表明,基体开裂方向与纤维方向平行,而基体的压溃主要发生在刀尖周围. 熊威龙等[8]模拟得到了崩碎切屑的形成过程、切削力随刀具行程的变化曲线、应力在刀具及工件中的分布. 秦旭达等[9]模拟研究不同铺层的CFRP在切削过程中受到的应力,结果表明,应力分布与纤维方向相一致. Santiuste等[10]分别建模研究了玻璃纤维复合材料(GFRP)和CFRP切屑形成和基体损伤,GFRP的损伤广泛分布在刀尖前面和下面区域,而CFRP的损伤区域小的多. Iliescu等[11]采用离散有限元法(DEM)模拟单向CFRP正交切削切屑的形成过程和切削力. 然而,计算过程中需要确定所有的粒子之间的接触,特别是当接触区域是复杂的情况下会导致大量的计算. Zenia等[12]将弹塑性理论与损伤联系起来实现了切屑的连续形成过程,并且考虑了相关工艺参数对材料失效破坏的影响.
综上分析,CFRP宏观建模研究主要集中于切削力、切屑形成和损伤失效等方面,而对于CFRP切削过程中的能量耗散以及切削加工质量问题研究较少,而能量耗散以及切削加工质量直接影响到刀具的性能以及工件的使用寿命. 因此,基于Hashin失效准则[13]及其刚度退化理论建立CFRP切削动态物理仿真模型,研究切削速度和切削深度对CFRP切削过程中的能量耗散以及不同纤维方向和刀具结构的切削加工质量问题,为实际加工提供理论参考.
1 CFRP切削仿真模型建立
1.1 几何建模及边界条件

图1 CFRP有限元模型Fig.1 CFRP finite element model
采用有限元软件ABAQUS/Explicit模块建立复合材料切削有限元仿真模型[8]. 将复合材料定义为均质等效宏观模型(EHM),纤维相与基体相并没有分开考虑. 通过定义材料方向来表征复合材料的纤维方向(E11)与纤维方向垂直方向(E22),以此来定义材料宏观结构上的正交各向异性[7]. 在动态显式分析过程中,工件材料采用平面应力线性插值缩减积分四节点单元(CPS4R),自动沙漏控制. 切削过程中刀具和工件之间的接触设置为面面接触,并对刀尖区域及其周围的工件网格进行了细化,其余地方划分网格较为粗糙. 刀具采用平面应力线性插值缩减积分三节点单元(CPS3R),自动沙漏控制. CFRP切削仿真模型的基本几何结构如图1所示. 其中:α为刀具前角,β为刀具后角,αp为切削深度,v为切削速度,θ为纤维方向角度. 工件底部边界采用完全固定约束; 左右两边边界采用水平方向固定,为了与有关实验成果进行对比,选取的刀具参数为:α=0°,β=6°.
在建立有限元模型时,为提高计算效率及计算精度,在构建的几何模型中采用以下假设和简化:
1) 因为在复合材料切削加工时,形成的不连续切屑使刀具与切屑的接触长度范围大约为10~100 μm,因此,摩擦在前刀面上产生的热量是很小的,可忽略不计;
2) 摩擦在刀具后刀面上产生的温度远低于基体的融化温度,因此不考虑温度场的分布;
3) 切削过程为准静态过程,这个假设是基于碳纤维复合材料由于脆性纤维主导作用而显示很小的应变率依赖性;
4) 将刀具定义为刚体,不考虑其变形以及温度场,并耦合在一个参考点上控制其运动.
1.2 材料与损伤失效准则
文中模拟研究的材料为单向碳纤维/环氧复合材料T300/914,其机械物理性能如表1所示.

表1 T300/914材料性能[14]
为模拟纤维/基体系统破裂,采用Hashin破坏准则进行数值模拟. Hashin破坏准则考虑在复合材料切削加工过程中通常出现的纤维拉伸破坏、纤维压缩破坏、基体拉伸破坏、基体压缩破坏四个基本失效模式,如表2所示. 其中,σ11表示沿着纤维方向的应力,σ22表示垂直纤维方向的应力,σ12代表面内剪切应力.
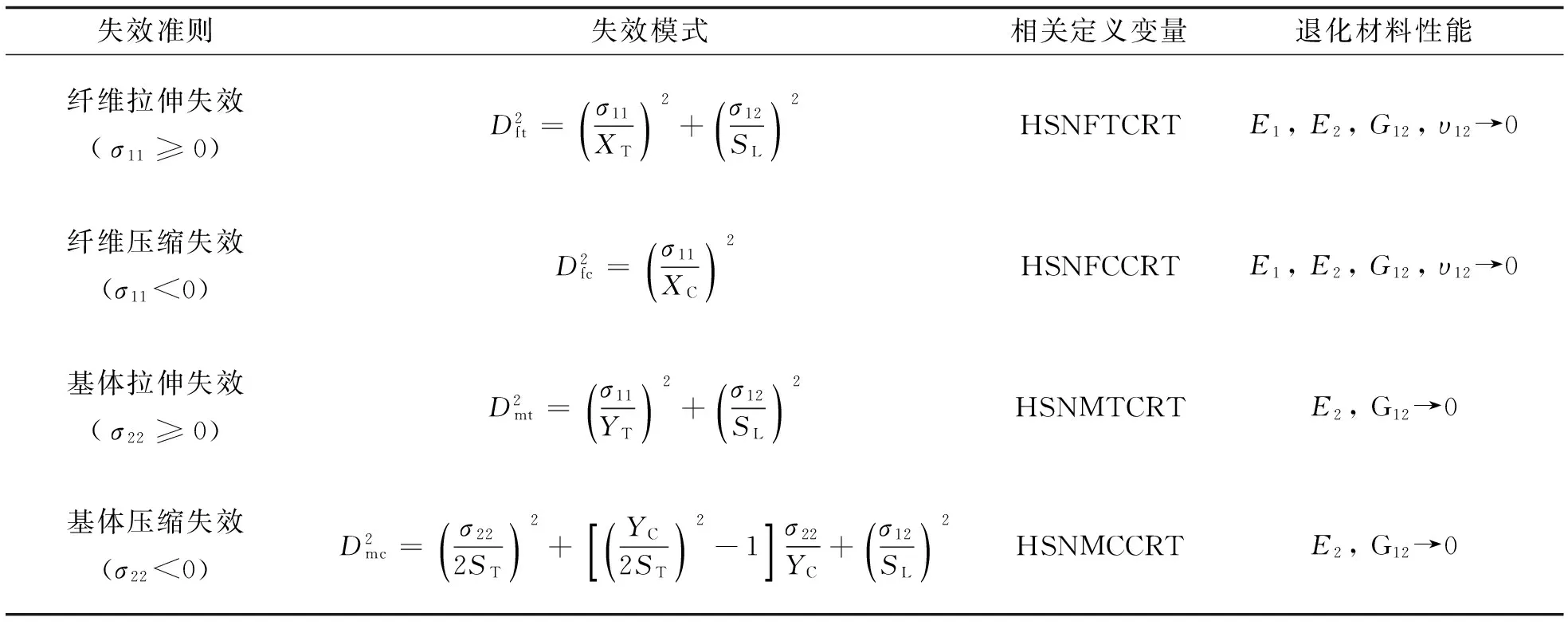
表2 CFRP的Hashin失效准则[14]
通过刚度退化理论对CFRP的单元失效进行分析,即当纤维/基体一种失效模式发生时,材料的性能会退化,如表2所示. 材料性能退化取决于四个相关变量,定义如下:1) 第一个变量HSNFTCRT表示代表纤维的拉伸破坏模式; 2) 第二变量HSNFCCRT代表纤维压缩破坏模式; 3) 第三个变量HSNMTCRT代表基体拉伸破坏模式; 4) 第四变量HSNMCCRT代表基体压缩破坏模式. 在有限元计算中,对每个积分点的材料特性进行评定,退化取决于采用的失效模式. 如果任何失效阈值达到1,相关的材料特性会根据实施的刚度退化方案自动降低到零,该过程会不断地重复,直到完成切屑的形成[14].
1.3 力学建模及分析

图2 CFRP正交切削受力分析图[15]Fig.2 Force analysis of CFRP orthogonal cutting[15]
碳纤维复合材料在切削时的剪切面有两个:一个沿纤维方向,即图中的AC面; 另一个平行于纤维方向,即图中的BC面. 纤维首先沿AC面剪断,然后沿BC面滑出,进而成为切屑,如图2所示[15]. 由图2可得出以下公式:
其中:Fs1为垂直于纤维方向切断纤维的作用力;Fs2为平行于纤维方向剪切断基体的作用力;Fx为主切削力;Fy为进给切削力;α为纤维与被加工材料对切削区的作用合力R′ 之间的夹角;β为切屑底部与刀具前刀面摩擦产生的摩擦角[15]. 将式(1)、(2)代入式(3)得:

设CFRP厚度为d,AC剪切面长度为l1,BC滑移面长度为l2,则:
式中:τ1、τ2分别为纤维横向剪切强度和基体剪切强度.
又:
由图2可得:
其中:ac为切削深度. 联立(5)、(6)、(7)三式得:
将(8)式代入(4)式,整理得出主切削力和进给切削力理论计算公式:
2 模拟结果与分析
2.1 切削比能研究
在正交切削加工过程中,切削速度和切削深度是两个重要的工艺参数,是力、热、摩擦磨损、加工缺陷等产生的重要影响指标. 研究切削速度和切削深度对CFRP的切削加工性能的影响可用切削比能u(MPa)[16]来反映,其主要表征在切削加工中去除单位体积材料所耗散的能量,这主要是由所研究材料的特性决定并且可以反映出材料的相对切削加工性[17]. 具体而言,在正交切削过程中,切削比能(u)可以用以下方程表示:
式中:PC为切削加工功率; MMR代表材料去除率(mm3·s-1),分别表示如下:
式中:FC代表主切削力;vC代表切削速度;ap代表切削深度;w代表切削宽度. 由式(11)、(12)可得:
为计算方便, 将切削宽度w设为1 mm.
2.1.1 切削速度对切削比能的影响
图3所示为CFRP在不同切削速度下的切削比能谱图,仿真过程设定切削深度αp=0.05 mm. 切削比能谱图采用极坐标绘制,在极坐标系中,0°~180°半圆周范围内,极角代表纤维方向角度θ,对于180°~360°圆周范围的角度,可以描述为极角(θ)减去180°[17],半径R代表切削比能u的值. 其中,u根据公式(13)计算求得,FC为切削过程中稳定阶段主切削力的均值. 在0°~180°半圆周范围内,每隔15°纤维方向计算在设定的工艺参数下切削比能的值,180°~360°圆周范围内可进行相应极角推导,以此绘制CFRP切削过程中的切削比能谱图.
从图3中可以看出切削速度对切削过程中的能量耗散有显著影响,随着切削速度的增加,切削过程的能量耗散逐渐增大,切削比能谱图呈现扩张趋势. 这主要是因为切削速度的增大,刀具对工件的冲击作用增强; 同理,硬质纤维对刀具表面的刻划与摩擦加剧,导致能量耗散增大. 当速度为6 m·min-1时,各纤维方向的切削比能最小,切削加工性能最好. 当速度为6~18 m·min-1时,随着速度的增加,切削比能缓慢增大,切削比能谱图形状保持相对不变; 当速度为24 m·min-1时,各个纤维方向的能量耗散均有相对明显的增加,说明速度增大时,工件对刀具的反作用力增加较快,能量耗散大.

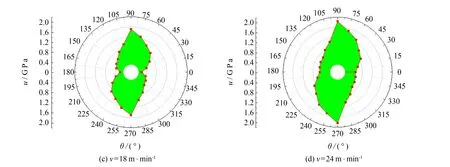
图3 不同切削速度切削比能谱图Fig.3 Specific cutting energy spectra of different cutting speeds
2.1.2 切削深度对切削比能的影响
图4为CFRP在不同切削深度的切削比能谱图,仿真过程设定切削速度v=6 m·min-1. 由图4可见,随着切削深度的增加,切削比能谱图呈现出逐渐收缩的趋势,说明去除单位体积材料所耗散的能量逐渐减少,这与Sreejith等[18]的实验研究成果相吻合. 因此,根据式(13)可知,随着切削深度的增加,切除的材料体积增大,切削力增大的趋势变缓. 当切削深度为0.05 mm时,纤维方向为90°的切削比能相对纤维方向为105°的切削比能有较明显差异,随着切削深度的增加,这种差异逐渐减弱; 在切削深度αp为0.1~0.2 mm时,切削比能谱图均匀收缩,说明切削深度对不同纤维方向的切削比能的影响权重近视.
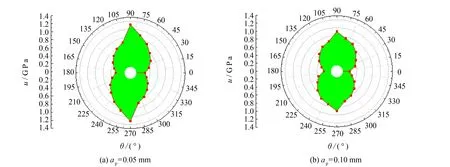
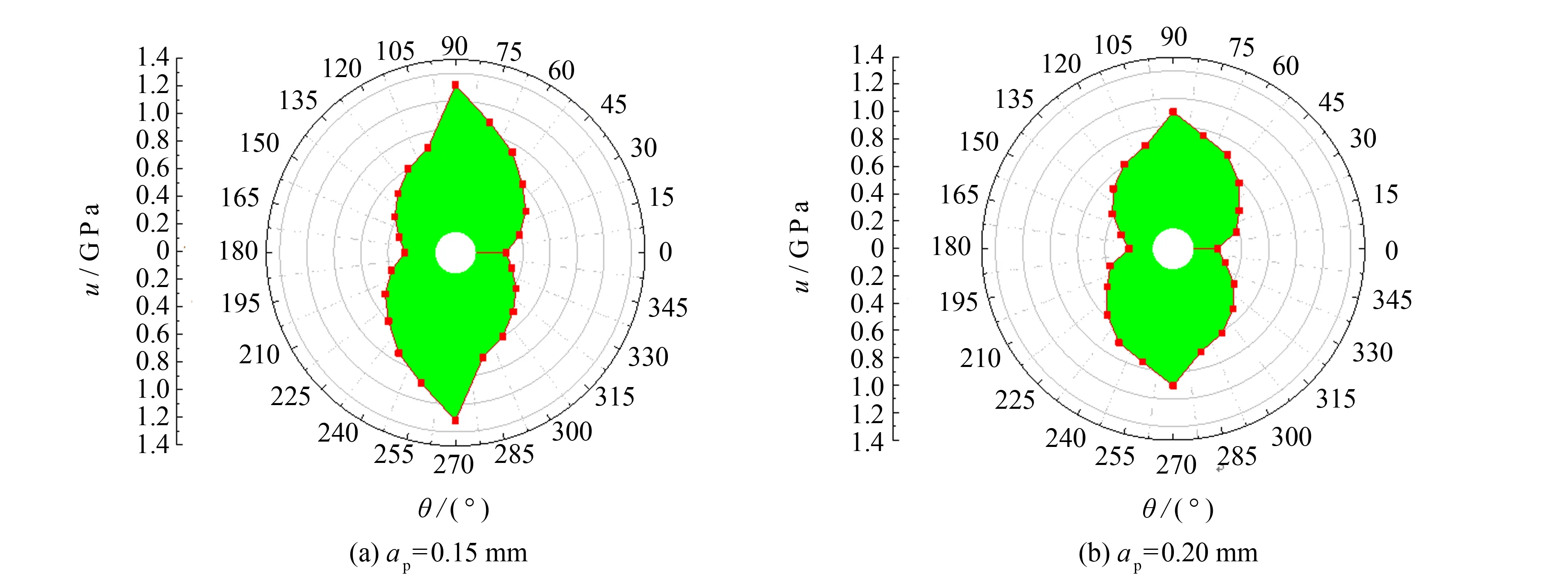
图4 不同切削深度切削比能谱图Fig.4 Specific cutting energy spectra of different cutting depths
同时,从图3和图4可见,切削比能具有显著的各向异性,在不同纤维方向上差异较大. 当θ=0°时,刀具运动过程中不断挤压纤维并且破坏纤维与基体的粘结界面,即界面层剥离和纤维挤压断裂为主要切断机制. 纤维方向角度从0°到90°,为顺纤维方向切削,随着纤维方向角度的增加,刀具对纤维的作用力,可分解为沿纤维方向的拉伸作用力和垂直于纤维方向剪切作用力,因此,纤维破坏的方式逐渐由挤压破坏转变为拉伸和剪切破坏. 由于纤维的压缩强度比纤维拉伸强度小,且界面强度相对材料性能强度较小,因此,切削0°纤维方向的能量耗散最小. 当θ=90°时,被刀具压断或剪断的纤维数达到最大,而碳纤维和基体材料的压缩强度极限和剪切强度极限都较高,对刀具反作用力大,且切屑不易排出. 因此,90°纤维方向在切削过程中的能量耗散最大.
纤维方向角度从90°到180°,为逆纤维方向切削,随着角度的增加,切削比能逐渐减小. 从图3中可以看出,105°纤维方向的切削比能相对90°纤维方向的切削比能有一个骤降的趋势,主要是因为逆纤维方向切削时,纤维的失效形式主要为弯曲断裂为主,而纤维的弯曲强度相比拉伸强度要小,因此所需要的能量耗散相对比顺纤维方向切削要小. 随着纤维方向角度的进一步增大,参与切削的纤维数逐渐减小,工件对刀具的反作用力减小,因而切削比能降低.
2.2 切削加工质量评定分析
2.2.1 纤维方向对切削加工质量的影响
CFRP切削加工仿真结果如图5所示,被去除的切屑形态呈现“粉末”状的形状,这主要是由CFRP脆性断裂的切屑分离模式占主导地位引起的. 当θ=0°时,切削加工表面并未出现明显的凹坑和裂纹,这与其切屑为层间分离型密切相关. 切屑主要由纤维与基体界面层剥离以及材料的压溃形成的,切削变形发生在通过刀刃点的水平面以上的部位,因此,0°纤维方向的切削加工表面较为平整. 当θ=45°时,切屑形成形式为纤维切断滑移型,在刀具的作用下,材料较容易沿纤维方向滑移去除. 然而,材料在滑移去除过程中也容易发生纤维拔出导致凹坑缺陷,并且在前刀面形成沿纤维方向的滑移破坏,如图5(b)所示,对未切削或者不需要切削的材料造成破坏.
当θ=90°时,刀具切削方向与纤维方向相垂直,当材料被去除之后刀具会对未切除的材料产生垂直于纤维方向的压应力,当此应力超过纤维与基体的粘结强度时,会导致纤维与基体脱粘,形成微裂纹,并在刀具进给过程中的不断作用下向下扩展,最终形成表面裂纹. 当θ=135°时,切削加工表面可以看到严重的加工缺陷,并且分布方向大致与纤维方向一致. 切削过程在刀具的作用下,材料不断发生弯曲. 当弯曲应力达到CFRP的弯曲极限时,材料发生断裂. 弯曲应力的最大点在刀尖的下方,因此断裂点位于加工平面之下,并且有向工件材料内部进一步扩散的趋势,这样就会导致在材料去除之后在加工表面下方形成空隙和凹坑.θ为90°和135°的仿真结果与Zitoune等[19]所进行的CFRP正交切削实验观察到的加工缺陷趋势相吻合.


图5 不同纤维方向切削形貌图Fig.5 Cutting morphology of different fiber orientations
2.2.2 刀具结构对切削加工质量的影响
针对90°纤维方向的CFRP易产生破坏缺陷的问题,探究了刀具结构对其切削加工质量的影响规律. CFRP切削加工过程主要是前刀面不断与工件接触实现材料去除的过程,因此研究刀具前角对CFRP切削加工质量的影响具有重要的现实意义. 如图6所示,随着刀具前角的增大,CFRP的切削破坏缺陷程度随之减轻,切削加工质量得到改善. 刀具前角的增大,使得材料断裂方式逐渐变为刀具直接切断型,对亚表面造成的损伤破坏减小.

图6 不同刀具前角90°纤维方向切削加工质量Fig.6 The cutting quality of 90° fiber orientation in different tool rake angles
3 结语
1) 切削参数对切削过程中的能量耗散有显著影响,随着切削速度的增加,切削过程的能量耗散逐渐增大,切削比能谱图呈现扩张趋势; 而切削深度对其有相反的影响,随着切削深度的增加,切削比能谱图呈现出逐渐收缩的趋势.
2) 切削比能具有显著的各向异性,不同纤维方向上的切削比能差异较大. 0°纤维方向的能量耗散最小,90°纤维方向的能量耗散最大. 0°<θ< 90°为顺纤维方向切削,随着纤维方向角度的增加,切削比能逐渐增大; 90°<θ< 180°为逆纤维方向切削,随着角度的增加,切削比能逐渐减小,其切削比能相对比顺纤维方向切削要小.
3) 切削加工质量随着纤维角度的变化有明显的差异. 纤维方向θ为0°和45°的切削加工表面较为平整,但45°纤维方向会出现凹坑和滑移破坏缺陷; 纤维方向θ为90°和135°有明显的加工裂纹缺陷; 随着刀具前角的增大,90°纤维方向的切削加工质量得到改善.
[1] 马刚峰,李峰,徐泽夕,等. 聚丙烯腈基碳纤维研究进展[J]. 现代纺织技术,2011,19(3): 58-64.
[2] 高汉卿,贾振元,王福吉,等. 基于细观仿真建模的CFRP细观破坏[J]. 复合材料学报,2016,33(4): 758-767.
[3] AROLA D, RAMULU M. Orthogonal cutting of fiber-reinforced composites: a finite element analysis[J]. International Journal of Mechanical Sciences, 1997, 39(5): 597-613.
[4] RAMESH M V, SEETHARAMU K N, GANESAN N,etal. Analysis of machining of FRPs using FEM[J]. International Journal of Machine Tools & Manufacture, 1998, 38(12): 1 531-1 549.
[5] LASRI L, NOUARI M, EL-MANSORI M. Modelling of chip separation in machining unidirectional FRP composites by stiffness degradation concept[J]. Composites Science & Technology, 2009, 69(5): 684-692.
[6] MAHDI M, ZHANG L. A finite element model for the orthogonal cutting of fiber reinforced composite materials[J]. Journal of Materials Processing Technology, 2001, 113(1): 373-377.
[7] 路冬,李志凯,融亦鸣,等. 基于宏观各向异性碳纤维增强树脂基复合材料的切削仿真[J]. 复合材料学报,2014,31(3): 584-590.
[8] 熊威龙,戴斌煜,商景利,等. 碳纤维复合材料切削过程的有限元模拟[J]. 兵器材料科学与工程,2014,37(1): 86-89.
[9] 秦旭达,李永行,王斌,等. CFRP纤维方向对切削过程影响规律的仿真研究[J]. 机械科学与技术,2016,35(3): 472-476.
[10] SANTIUSTE C, SOLDANI X, MIGUELEZ H M. Machining FEM model of long fiber composites for aeronautical components[J]. Composite Structures, 2010, 92(3): 691-698.
[11] ILIESCU D, GEHIN D, IORDANOFF I,etal. A discrete element method for the simulation of CFRP cutting[J]. Composites Science & Technology, 2010, 70(1): 73-80.
[12] ZENIA S, AYED B L, NOUARI M,etal. Numerical prediction of the chip formation process and induced damage during the machining of carbon/epoxy composites[J]. International Journal of Mechanical Sciences, 2015, 90: 89-101.
[13] HASHIN Z, ROTEM A. A fatigue failure criterion for fiber reinforced materials[J]. Journal of Composite Materials,1973(7): 448-464.
[14] XU J Y, MANSORI M E. Cutting modeling of hybrid CFRP/Ti composite with induced damage analysis[J]. Materials, 2016, 9(1): 1-22.
[15] 张厚江,陈五一,陈鼎昌,等. 碳纤维复合材料切削机理的研究[J]. 航空制造技术,2004(7): 57-59.
[16] SHAW M C. Metal cutting principles[M]. New York: Oxford University Press, 2005.
[17] XU J Y, MANSORI M E. Numerical studies of frictional responses when cutting hybrid CFRP/Ti composite[J]. International Journal of Advanced Manufacturing Technology, 2016, 87(1/2/3/4): 657-675.
[18] SREEJITH P S, KRISHNAMURTHY R, MALHOTRA S K,etal. Evaluation of PCD tool performance during machining of carbon/phenolic ablative composites[J]. Journal of Materials Processing Technology, 2000, 104(1): 53-58.
[19] ZITOUNE R, COLLOMBET F, LACHAUD F,etal. Experiment-calculation comparison of the cutting conditions representative of the long fiber composite drilling phase[J]. Composites Science and Technology, 2005, 65(3): 455-466.

