激光与近相对论临界密度薄层相互作用产生大电量高能电子束∗

王剑 蔡达锋 赵宗清 谷渝秋

1)(内江师范学院物理学与电子信息工程学院,内江 641110)

2)(中国工程物理研究院激光聚变研究中心,绵阳 621900)

1 引 言

超高强激光产生X射线源研究是目前强场研究领域热点问题之一.目前主要有两种技术途径:一种是利用激光直接与高Z固体靶作用[1,2].但是高Z固体靶对激光有很高的反射率,会损失很大一部分激光能量,影响了更大电量超热电子束的产生.为此研究人员提出了各种不同靶型,如天鹅绒靶[3]、多孔靶[4]、亚波长光栅靶[5],团簇靶[6]、纳米刷靶等[7]多种靶构型,用以提高激光到超热电子的转换效率,引导和准直超热电子.但即使如纳米刷靶能够将激光的吸收提高到激光总能量的80%,为普通平面靶的2倍,电子束的截止能量以及平均温度也不是很高.根据Hu等[5]报道的结果,电子束截止能量只能达到几个MeV,平均温度也仅1.3 MeV.此外,由Hanies第[8]给出的定标率,激光与有限密度梯度等离子体相互作用时,即使功率密度达到1021W/cm2,高能电子束的平均温度仍然不超过5 MeV,仍然低于Wilks定标率的估计[9].另一种是利用超高强激光与气体靶作用产生激光尾波场电子,激光尾波场再通过与高Z转换靶相互作用或者Betatron类同步辐射的方式产生X射线[10−12].2004年以来,激光尾波场电子加速器技术研究取得了重大进展,各研究小组相继报道了通过激光尾场电子加速获得数十MeV乃至GeV量级的准单能电子束的结果[13−16].然而,由于等离子体空泡中难以注入大量的电子,通过空泡机制产生的高能电子束所包含的电子束总电量难以达到nC量级,这一特性限制了电子束在超亮微焦点X射线源的产生及其在透视照相等方面的应用.本文研究了激光与近临界密度等离子体薄层相互作用所产生的高能电子束平均有效温度(“斜坡温度”)以及截止能量等特征.研究表明空泡机制可以产生nC级高能电子束,平均有效温度可达8 MeV以上,为将来产生高性能X射线源提供了一种新的途径.

2 实 验

实验是在中国工程物理研究院激光聚变研究中心星光III升级激光装置上进行.实验排布如图1所示,1053 nm皮秒主激光经过f/3离轴抛物面镜聚焦在靶面上,光学焦斑的尺寸大约为10µm(FWHM).在主激光到达之前存在着持续1 ns的预脉冲,激光对比度为106—107.激光与靶面法线的夹角为10°.靶后激光出射方向放置一台6000 Gs磁谱仪,所测量电子能量范围为0—40 MeV.为了实时监测主激光的聚焦情况,我们在靶前放置了一套软X射线针孔相机.

图1 (网刊彩色)实验布局Fig.1.(color online)The con figuration of the experiment.

实验中采用了一种三醋酸纤维素泡沫靶,泡沫纤维丝直径20—30 nm,网孔间距10—100 nm,整块泡沫薄膜厚度为10µm,平均密度为10 mg/cm3,全离化对应的等离子体密度为3.1×1021/cm3.这是目前实验上所能得到的最低密度靶.1053 nm激光对应的临界密度为1.0×1021/cm3,预脉冲不能穿透泡沫薄膜,因此除了趋肤层为激光直接烧蚀外,其余部分为热传导层烧蚀.我们可以根据理论公式来定性地估计烧蚀的速度以及烧蚀的温度,临界面处的烧蚀温度为[17]

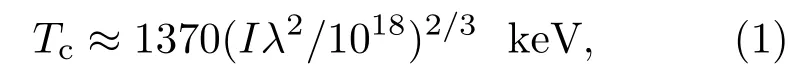
其中功率密度I单位是W/cm2,激光波长λ的单位为 µm.考虑到激光对比度为107,当主激光脉冲功率密度为5.0×1019W/cm2时,相对应的预脉冲的功率密度为5.0×1012W/cm2,代入(1)式,Tc≈0.43 keV,远远超过CH材料的离化阈值,材料被激光照射的区域可以被全部离化.预脉冲持续1 ns,则预计烧蚀深度可达520µm,远大于泡沫薄膜靶的厚度.即使考虑泡沫网格的影响,烧蚀波的传播速度比理论预计的低一个数量级,预脉冲也具有充足的时间可以将我们实验中采用的泡沫薄膜靶全离化,形成大尺度的近相对论临界密度等离子体.

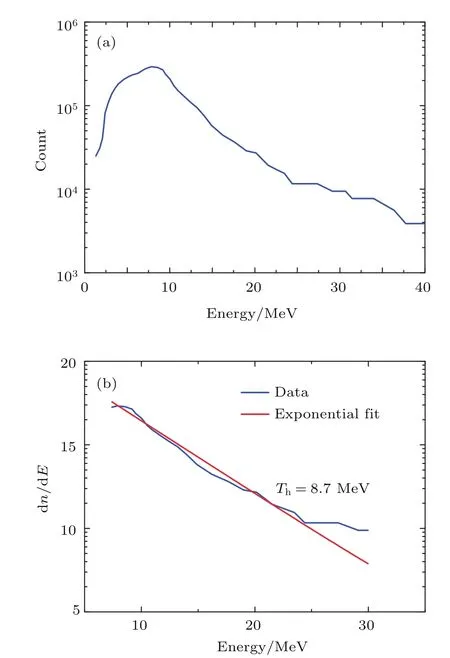
图2 (网刊彩色)1#发次电子能谱及平均有效温度(a)电子能谱;(b)指数拟合平均有效温度Fig.2.(color online)Electron spectrum and average effective temperature of 1#shot:(a)Electron spectrum;(b)average effective temperature by exponential fitting.

图2所示为1#发次靶后激光出射方向的超热电子能谱,对应的入射激光能量115 J,脉冲宽度0.9 ps,激光功率密度1.9×1019W/cm2.整个能谱大致呈类玻尔兹曼分布,谱峰的位置在9 MeV,截止能量超过35 MeV.如果对能谱进行指数拟合,我们发现拟合得到的平均有效电子温度为8.7 MeV,远远高于Wilks定标率给出的平均温度0.6 MeV[9].图3显示的是2#发次的电子能谱,相应的入射激光能量为72.8 J,激光脉冲宽度为0.6 ps,激光功率密度与1#靶对应的相同,其他参数保持不变.图3(a)可以看出,类玻尔兹曼分布的电子能谱的峰值8 MeV,而能谱的截止能量超过了40 MeV.对能谱进行指数拟合,电子束的平均有效温度(“斜坡温度”)为11.9 MeV,如图3(b)所示,同样远远高于有质动力定标率预言的温度.3#和4#发次分别对应激光能量为61 J和73 J、脉冲宽度0.3 ps时的情形,得到的平均有效电子温度为15 MeV.而激光能量73 J时,平均有效电子温度则为11 MeV.考虑到打靶过程中的激光器状态的起伏,两者的温度有一些差别.为了便于比较,我们将上述1#,2#,3#,4#靶对应的电子束平均有效温度放置在一张图中,如图4所示,横坐标为激光功率密度,图中误差棒所代表的误差主要来自于激光焦斑尺寸的误差.虽然误差较大,但是所有的数据点仍然显示出我们实际测量得到平均有效电子温度相较于Wilks定标率有了数倍的提高.

图3 (网刊彩色)电子能谱及平均有效温度 (a)2#发次靶后激光入射方向的超热电子能谱;(b)指数拟合平均有效温度Fig.3.(color online)Electron spectrum and average effective temperature of 2#shot:(a)Electron spectrum;(b)average effective temperature by exponential fitting.

电子束的电量是我们所关心的另一方面.对记录电子能谱的IP板进行空间积分,可以获得接收立体角内的总电子数.靶后激光出射方向的电子谱仪离靶的距离为66 cm,谱仪准直孔的大小为4 mm×5 mm,相应的接收立体角为0.003 sr.根据标定实验的结果,能量在0.5 MeV以上的电子,每个荧光光子对应的电子数为100,因此我们可以初步得到IP板记录的电子数量.对2#发次IP板进行积分,我们获得1#发次的电量为6.6 nC/sr.类似地,我们可以得到2#发次的电量为6.1 nC/sr.

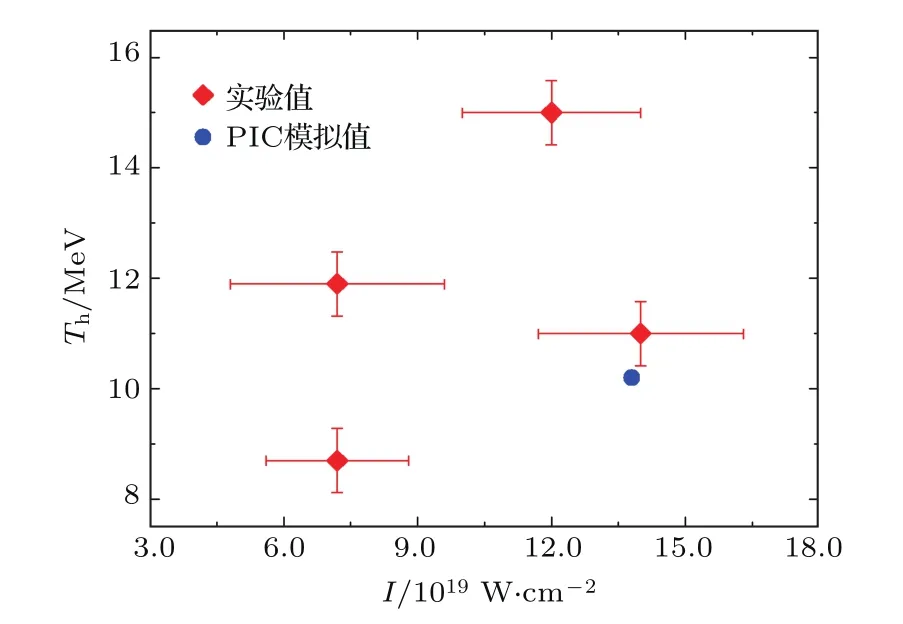
图4 (网刊彩色)电子束温度与激光功率密度的关系Fig.4.(color online)The dependence of temperature on laser power density.

3 分析讨论

相对论激光与稠密等离子体相互作用时,有质动力加速占主要地位[9,18].但是,我们实验中的电子束平均有效温度远远高于Wilks定标率的预计[9].因此,我们不得不考虑其他加速机制的贡献.为了更好地理解其中的大电量高能电子束产生的物理机制,我们采用二维粒子模拟程序进行了模拟研究.模拟参数与实验参数基本相同.模拟盒子大小为100λ×40λ,λ=1µm是激光波长,共2000×800个网格,每个网络放置32个宏观粒子.碳等离子体层放置在模拟盒子中部,初始电子密度设置为ne=3.6nc,nc=1.1×1021/λ2cm−3,厚度为10µm.在主脉冲到达之前有持续1—2 ns的预脉冲,根据类似的二维维流体力学模拟[19,20],我们在等离子体之前设置了一段密度梯度L=5λ的预等离子体.电子和离子的初始温度分别设置为300 eV和10 eV.一束P极化激光垂直地入射到靶上,激光归一化振幅a0=eE/meω=10,τ=80T,激光焦斑的半高全宽w=6µm(FWHM),其中me为电子质量,ω为激光频率,T为激光周期.

图5(a)—(c)是不同时刻的电子密度分布,分别对应着40T,80T,120T.首先可以看到,40T时,激光在次稠密等离子体中传播,有质动力将电子推开,堆积在两侧,形成一个狭窄的等离子体通道.等离子通道的宽度与激光焦斑的大小相当.80T时,由于相对论自透明和钻孔效应[21],激光不仅能在次稠密等离子体中传播,还能进入到密度高于临界密度的区域,也就是近相对论临界密度区域,即ne～ γnc,其中通过激光成道形成一条更长的等离子体通道.从激光波前的位置我们可以推断出激光向前传输的速度约0.2c,c为光速.成道速度介于激光钻孔速度=0.08c和激光群速度=0.76c之间,其中mi为离子质量.激光可以在较短时间内将等离子体完全烧穿,形成一条数十微米的短等离子体通道,与我们的预期相符.至120T时,激光已经“烧穿”该等离子体,形成一条长30µm左右的等离子体通道.此时,考虑到离子开始膨胀,等离子体通道的宽度变得更宽,并开始出现一些丝状结构,该丝状结构由离子运动引起.

与此同时,我们诊断了等离子体通道周围的周期平均电磁场,磁场大小使用meωc/e归一化.如图6(a)所示,该磁场为角向分布,即垂直于纸面的Z方向,包围了整个等离子体通道区域.一般认为,高能电子流在等离子体通道的外部创建了该自生磁场,磁场的最大值可达500 MGs.该结果与文献[21]给出的结果相似.事实上,考虑到图5所示的离子体通道主要是通过相对论自透明效应和激光钻孔效应共同形成[21],电子与离子都会被有质动力从等离子体通道中排开,形成排空结构,因此等离子体通道中不能形成有规律的电荷分离电场,如图6(b)所示.

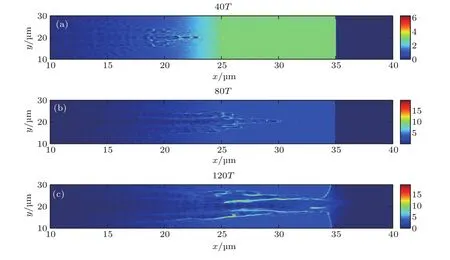
图5 (网刊彩色)电子密度随时间的演化 (a)40T时的密度;(b)80T时的密度;(c)120T时的密度Fig.5.(color online)Snapshot of electron density at different times:(a)At 40T;(b)at 80T;(c)at 120T.

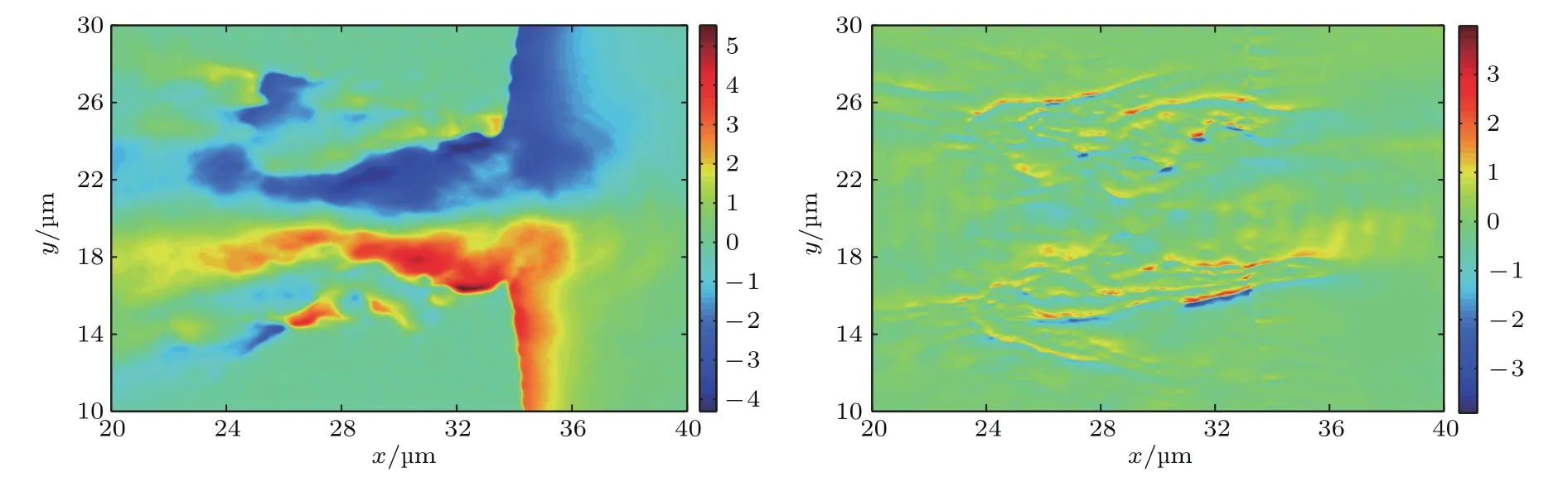
图6 (网刊彩色)140T时的自生电磁场 (a)自生磁场;(b)自生电场Fig.6.(color online)The self-generated electromagnetic field at 140T:(a)Self-generated magnetic field;(b)self-generated electric field.

图7 (网刊彩色)不同偏振态的电子能谱Fig.7.(color online)The electron spectrum for different laser polarization.

图7中绿线显示的是上述模拟所获的电子能谱.整个电子能谱呈类玻尔兹曼分布,电子的截止能量超过90 MeV.我们对电子能谱的高能部分进行指数拟合,发现电子束平均有效温度(“斜坡温度”)为10.2 MeV.实验研究和理论研究都表明,激光在等离子体通道内通过Betatron共振加速机制直接加速电子[22−24],这部分电子束的截止能量和平均有效温度很高.显然,由相对论自透明和钻孔效应所形成的等离子体通道内,同样可以发生Betatron共振加速,只是由于缺乏自生电场的作用,Betatron共振的频率会变小一些[24].最终,模拟中所获电子束的平均有效温度和实验值一样,均超过了Wilks定标率的预计.此外,我们改变激光的偏振方向,将P偏振变为S偏振,而保持模拟激光和等离子体参数不变.显而易见,图7中蓝线显示的电子能谱的截止能量和平均有效温度都大幅降低.就截止能量而言,S偏振仅是P偏振的40%;平均有效温度S偏振也仅是P偏振的50%.考虑到模拟程序是二维的,因此,只有P偏振的情况下,激光场才会与电子发生共振,从而将电子直接加速到很高的能量.虽然模拟中P偏振和S偏振激光获得的电子能谱有较大差别,但是实验中的物理过程是三维的.在入射角比较小时,S偏振和P偏振没有显著的差别,从另外一个角度说明实验中平均有效温度如此高的原因在于Betatron共振直接加速.遗憾的是,实验中使用的电子谱仪的测量范围有限,没有测得如模拟中所示的更高能量的电子.

4 结 论

本文报道了激光与近相对论临界密度等离子体相互作用研究结果.实验结果与理论分析均证实,在相对论自透明效应和激光钻孔效应共同作用下,近相对论临界密度等离子体内将出现磁化等离子体通道,电子与激光在通道周围角向磁场的协助下发生Betatron共振.在我们实验参数范围内,高能电子的平均有效温度在6—12 MeV之间,高于Wilks定标率预言的平均温度.本研究有助于激光与近相对论临界密度等离子体相互作用的理解,并为下一步高亮度γ射线源以及正电子源产生奠定了一定基础.

[1]Jarrott L C,Kemp A J,Divol L,Mariscal D,Westover B,McGu ff ey C,Beg F N,Suggit M,Chen C,Hey D,Maddox B,Hawreliak J,Park H S,Remington B,Wei M S,MacPhee A 2014Phys.Plsamas21031211

[2]Westover B,MacPhee A,Chen C,Hey D,Ma T,Maddox B,Park H S,Remington B,Beg F N 2010Phys.Plsamas17082703

[3]Kulcsár G,AlMawlawi D,Budnik F W 2000Phys.Rev.Lett.845149

[4]Nodera Y,Kawata S,Onµma N 2008Phys.Rev.E78046401

[5]Hu G Y,Lei A L,et al.2010Phys.Plasmas17083102

[6]Huang K,Li D Z,Yan W C,Li M H,Tao M Z,Chen Z Y,Ge X L,Liu F,Ma Y,Zhao J R,Hafz N M,Zhang J,Chen L M 2014Appl.Phys.Lett.105204101

[7]Cao L H,Gu Y Q,Zhao Z Q 2010Phys.Plasmas17043103

[8]Haines M G,Wei M S,Beg F N,Stephens R B 2009Phys.Rev.Lett.102045008

[9]Wilks S C,Kruer W L,Tabak M 1992Phys.Rev.Lett.691383

[10]Glinec Y,Faure J,Le Dain L,Darbon S,Hosokai T,Santos J J,Lefebvre E,Rousseau J P,Burgy F 2005Phys.Rev.Lett.94025003

[11]Cipiccia S,Islam M,Ersfeld B,Shanks R P,Brunetti E,Vieux G,Yang X,Issac R C,Wiggins S,Welsh G H,Anania M P,Maneuski D,Montgomery R,Smith G,Hoek M,Hamilton D J,Lemos N R C,Symes D,Rajeev P P,Shea V O,Dias J M,Jaroszynski D A 2011Nature Phys.7867

[12]Courtois C,Edwards R,Compant La Fontaine A,Aedy C,Barbotin M,Bazzoli S,Biddle L,Brebion D,Bourgade J L,Drew D,Fox M,Gardner M,Gazave J M,Lagrange J,Landoas O,Le Dain L,Lefebvre E,Mastrosimone D,PichoffN,Pien G,Ramsay M,Simons A,Sircombe N,Stoeck C,Thorp K 2011Phys.Plsamas18023101

[13]Kalmykov S Y,Gorburov L M,Mora P 2005Phys.Plasmas12033101

[14]Pukhov A,Gordienko S 2006Phil.Trans.R.Soc.A364623

[15]Lu W,Huang C,Zhou M 2006Phys.Plasmas13056709

[16]Esaresy E,Schroeder C B,Leemans W P 2009Rev.Mod.Phys.811229

[17]Atzeni S,Meyer-ter-Vehn J 2008The Physics of Inertial Fusion(in Chinese)(Beijing:Science Press)[Atzeni S,Meyer-ter-Vehn J 2008惯性聚变物理 (北京:科学出版社)]

[18]Kruer W L,Estabrook K 1985Phys.Fluids28430

[19]Scott R H H,Perez F,Santos J J,Ridgers C P,Davies J R,Lancaster K L,Baton S D,Nicolai Ph,Trines R M G M,Bell A R,Hulin S,Tzoufras M,Rose S J,Norreys P A 2012Phys.Plasmas19053104

[20]Pukhov A,Sheng Z M,Meyer-Ter-Vehn J 1999Phys.Plasmas62847

[21]Willingale L,Nagel S R,Thomas A G R,Bellei C,Clarke R J,Dangor A E,Heathcote R,Kaluza M C,Kamperidis C,Kneip S,Krushelnick K,Lopes N,Mangles S P D,Nazarov W,Nilson P M,Najmudin Z 2009Phys.Rev.Lett.102105002

[22]Kemp A,Sentoku Y,Tabak M 2008Phys.Rev.Lett.101075004

[23]Kemp A,Sentoku Y,Tabak M 2009Phy.Rev.E79066406

[24]Pukhov A,Sheng Z M,Meyer-ter-Vehn J 1999Phys.Plasmas62847