输电线路覆冰舞动区域的气象地理模型研究

汪 涛,周月华,朱昌成,黄俊杰,高正旭

（1.国网湖北省电力公司电力科学研究院，湖北 武汉 430077；2.武汉区域气候中心，湖北 武汉 430045）

0 引言

输电线路舞动是由于导线偏心覆冰改变了截面特性，在风激励下产生的一种低频、大振幅自激振动。输电线路覆冰舞动具有发生机理复杂、防治难度大和破坏力强的特点，是架空输电线路领域国际公认的难题[1-6]。

中国是输电线路舞动频发的国家之一，存在一条北起吉林，南至湖南的漫长的传统舞动带。在冬季由于特殊的气象因素满足了起舞的基本要素后，引起带状区域内各个电压等级的输电线路发生舞动[7-8]。辽宁省、湖北省、河南省是我国传统的强舞动区域。描述某一区域舞动强弱常用频率法，即对线路历史上实际发生的舞动情况进行统计分析，依据发生频率进行区域划分的方法[9-10]。

这种方法受已建线路的规模和数量影响较大，而且受舞动观测记录不全的影响，依据输电线路舞动发生频率很容易低估。此外，以舞动点5 km为半径划出区域，未考虑地形地貌的影响，依据不充分[11-12]。

仅仅依靠运行经验划分舞动分布图，不能真实反映线路运行实际情况，会误导防舞工作的有效开展，造成不必要的浪费。本文提出的“气象地理模型”，从输电线路舞动发生的气象机理入手，研究各种气象因子和地形地貌对线路舞动的影响，并结合运行经验，能全面、准确地划分舞动分布图并实现舞动的分区、分级，达到指导防舞设计和运行的目的。

1 舞动气象因子模型的建立

不同的气象要素对覆冰舞动的影响不尽相同，即便相关性均较好的几个气象要素，其对覆冰舞动的影响也可能具有重合的效果，选择其中有代表性的一个即可代表该类气象要素的影响，通过单要素相关性分析，分析12种气象要素（气压、平均气温、最高气温、最低气温、水汽压、相对湿度、最小相对湿度、20-20时降水、蒸发、风速、日照、08-08时降水共12种）对覆冰舞动的影响，可找出能够有效表征覆冰舞动的气象影响因子。

1.1 单要素关系分析

统计湖北从1988～2010年观测到的146条（次）输电线路覆冰舞动（归结为34个舞动日）案例，分析将每个案例所对应的12个气象要素，逐个给出不同区间段气象要素对覆冰舞动贡献的累积百分比，直观地得到该种气象要素在何种区间段对覆冰舞动贡献较大，可以得知该气象要素在某一较集中的区间范围内对覆冰舞动是否敏感。

12种气象要素的阈值分布及其对应的覆冰舞动累积百分比示意图见图1。

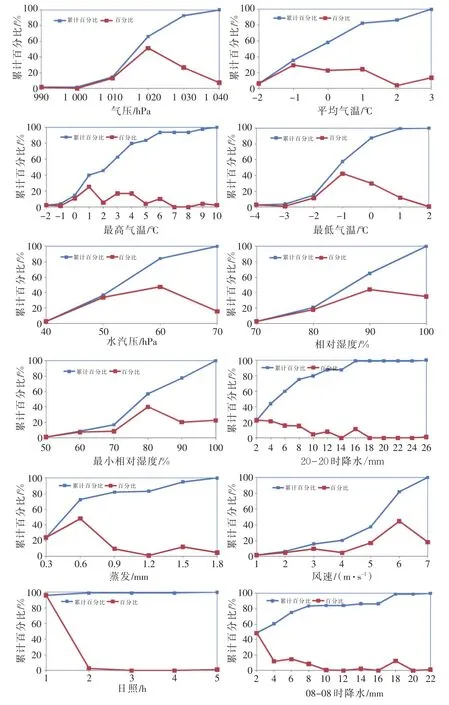
图1 12种气象要素阈值分布及其覆冰舞动累积百分比Fig.1 12 thresholds of meteorological elements and their cumulative percentage of galloping

从上面的分析可以得出，气压、最低气温、相对湿度和风速在特定区间对覆冰舞动是敏感的，表现在这4种气象要素在特定区间所对应的覆冰舞动累积百分比急剧增加并集中，说明该种气象要素在这段区间取值范围内，容易产生覆冰舞动。

表1列出了4种气象要素在覆冰舞动发生时的最小值、最大值和平均值。其中气压场在达到1 010～1 030 hPa时，覆冰舞动百分比增长最快，当气压场达到1 020 hPa以上时，表示有冷空气入侵。当最低气温在-3～1℃时，占了95%以上的覆冰舞动累积百分比；当相对湿度达到70%以上时，基本涵盖了所有覆冰舞动的发生概率；风速因子与覆冰舞动关系较明显的区间在5～7 m/s，由于这里的风速是全天的平均风速，覆冰舞动发生时的瞬时风速会远大于日内的平均风速，因此考虑将平均风速更换为日最大风速，以期能更好地反映风对覆冰舞动的影响。

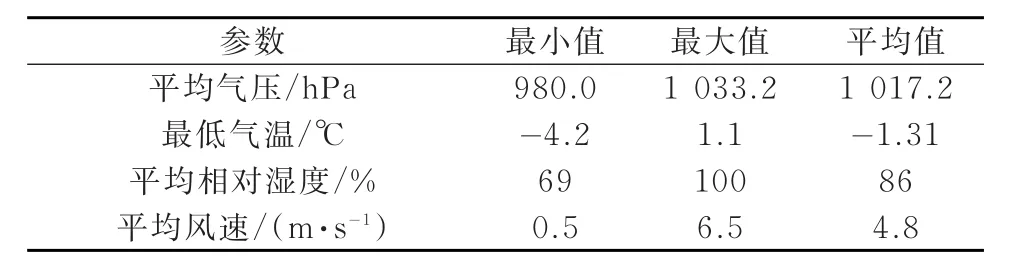
表1 4种气象要素阈值分布统计表Tab.1 Statistical distribution of 4 meteorological elements thresholds

1.2 高相关因子的选取

由于覆冰舞动发生的先决条件是覆冰、风速和风向，覆冰的发生与当日最低温度的关系较好，当最低气温接近于零度时，降水（包括可见的降水和大气中的水汽，可由相对湿度表征）可转化为覆冰，当风速和风向适合时，即可产生舞动。通过单要素的相关分析，可以判断影响覆冰舞动的主要气象因子是：最低温度、相对湿度、风速3个要素。

根据经验，覆冰舞动与风的关系很大，虽然平均风速能够部分反应与覆冰舞动的密切关系，但更精细的风的观测记录会更好地反映覆冰舞动与风的关系。同时，覆冰舞动不仅仅与风速密切相关，也与风向（线路与风的夹角）密切相关。因此，在最终的建模中，选取日最大风速和其对应的风向作为拟合因子，来表示风对覆冰舞动的影响。

从气候背景分析角度考虑，覆冰舞动的影响系统均为东北路冷空气。当东北路冷空气经过大别山区或鄂东山区时，在鄂西山区和大洪山的峡口效应下，鄂北中部至宜昌、荆门地区是湖北省风速较大的地区，同时也是舞动多发地区。因此，在考虑风速的影响时，需要引入风向作为建模时的显著影响因子。

通过覆冰舞动天气系统背景分析，可知覆冰舞动的主要影响系统是东北路冷空气，故选取北风和东北风向为主导风向时，最大风速的平均值作为待选的订正因子。两组订正因子的全省分布图如图2、图3所示。根据运行经验，北风风向下最大风速的分布较好反映了覆冰舞动灾害的分布特征，故选取北风风向下日最大风速作为覆冰舞动模拟风速影响因子。

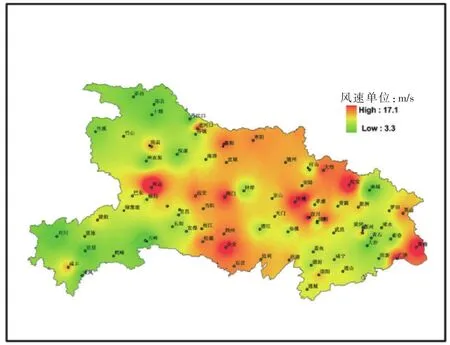
图2 1998～2010年11月至次年3月东北风向下湖北省日最大风速分布图Fig.2 Largest wind speed distribution in Hubei province from November to March of following year in 1998～2010 under the northeast wind

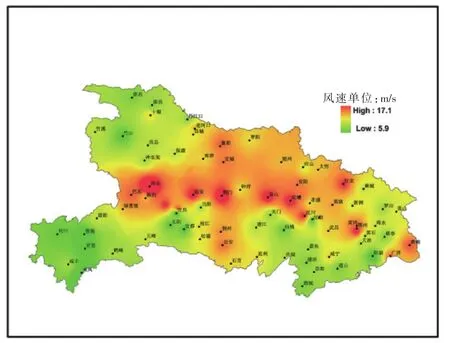
图3 1998～2010年11月至次年3月北风向下湖北省日最大风速分布图Fig.3 Largest wind speed distribution in Hubei province from November to March of following year in 1998～2010 under the north wind

1.3 组合要素模型建立

通过上述的单要素相关分析，可以判断与覆冰舞动相关较密切的几个气象因子分别是：日最低温度、日平均相对湿度、日最大风速和日最大风速对应的风向4个要素。

从天气系统背景分析得知，东北路冷空气天气系统是湖北省发生覆冰舞动的先决条件，风向上的特征表现为以偏北风向为主，随后的阈值统计均是以风向为偏北风向作为先决条件，即当日的最大风速所对应的风向为偏北风向的条件下，才有发生覆冰舞动的可能性。

在风向条件确定的基础上，统计146个覆冰舞动案例所对应的日最低温度、日平均相对湿度和日最大风速取值区间，可以得出模拟覆冰舞动是否发生的阈值分布结果：日最大风速所对应的风向为北风（包括东北风、西北风等偏北的风向），最大风速在5.8～13.7 m/s区间，最低气温在-4～1℃区间，日平均相对湿度≥70%，该条件覆盖所有覆冰舞动案例。

1.4 台站历史序列重建

通过上述气象要素模型，对湖北省78个观测台站1998～2010年11月至次年3月的逐日历史资料进行回算，统计78个台站13年的覆冰舞动总次数，并折算为年频次后进行10年总次数的分布图绘制，其分布图如图4所示。

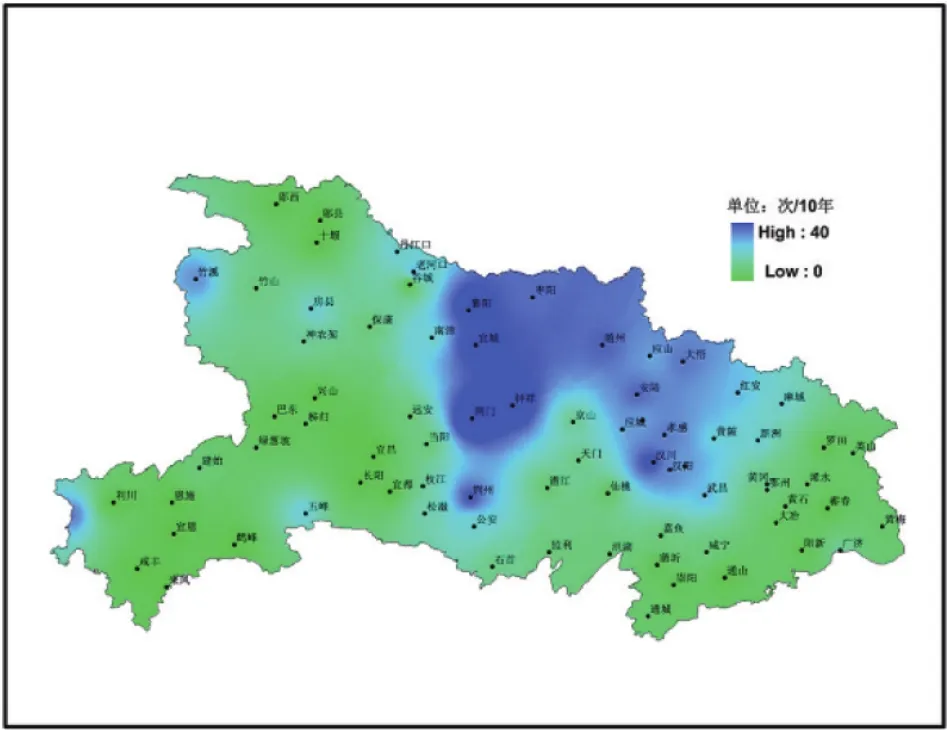
图4 湖北省舞动频次分布图（气象模型）Fig.4 Frequency distribution of galloping in Hubei province(weather model)

从图4可见，鄂北中部、宜城至钟祥、荆门一带和武汉周边地区维持覆冰舞动的大值区域，利川附近有一片覆冰舞动大值区域，其余区域均为覆冰舞动小值区域，但江汉平原的潜江、天门、仙桃地区，覆冰舞动的次数较小，这与该地区风速较小有关。

2 地形订正研究

覆冰舞动与局部地形的关系较为复杂。较为普遍的认识是：平原地区多发、丘陵地区次之，山区少见，且与海拔高度的相关性不明显，但丘陵和山区中的平原（微地形）线路仍然会发生舞动。针对这些因素，提出以“地形起伏度”指标来表征一定范围内的地势是否较为平坦，从而区分平原、丘陵和山区地形。

2.1 地形起伏度的选取

地形起伏度是指指定范围内最大相对高程差,它是描述一个区域地形特征的一个宏观性的指标，从其定义中可以看出，地形起伏度的实质仍是坡度概念的一个延伸。

通过对湖北146个覆冰舞动灾害案例统计归类，146次中，有20次属于同一灾害点多次发生灾害的，故不同的灾害点共有126个。其中100个标识为平原，丘陵16个，山区10个，这三类地形的地形起伏度（按照不同计算范围区分）变化范围如图5所示。

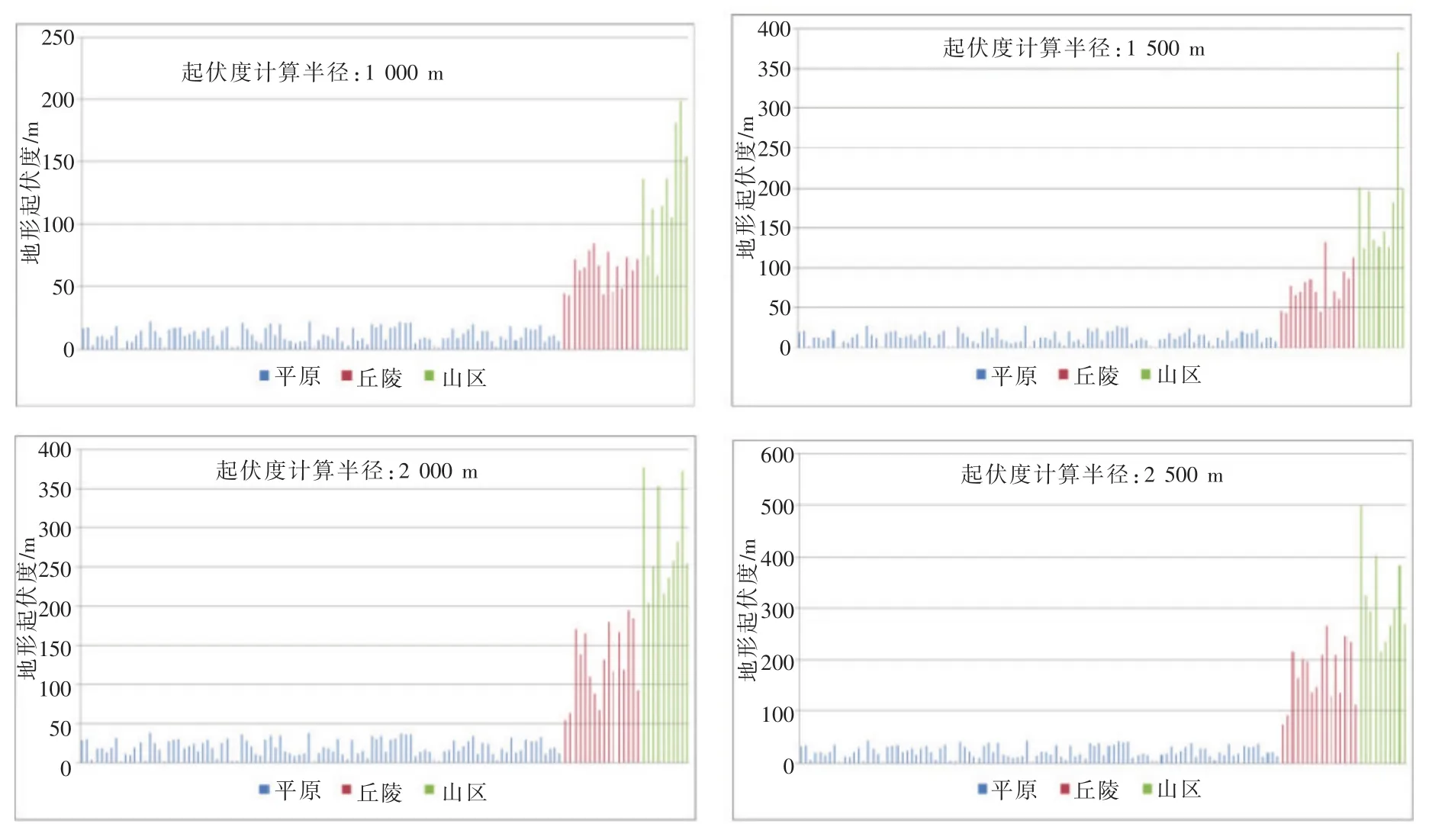
图5 不同计算半径下三种地形起伏度分布范围Fig.5 Distribution range of three kinds of terrain under different calculation radius

表2给出了不同计算半径下，三种地形的地形起伏度分布范围。

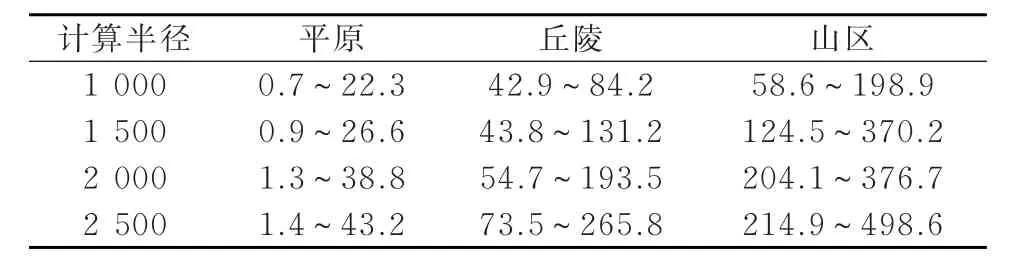
表2 不同计算半径下三种地形起伏度分布（单位：m）Tab.2 Distribution of three kinds of terrain under different calculation radius(unit:m)

从表2的统计数据可以看出，2 000 m左右的计算半径是较为合适的，在该半径范围内，三种地形没有明显的地形起伏度重叠，而另外三种计算半径，三种地形的地形起伏度重叠均较为明显，尤其是丘陵和山区不能有效分开，故选定2 000 m半径为地形起伏度计算半径。

2.2 定量订正关系

在2 000 m起伏度计算半径条件下，通过建立78个观测台站地形起伏度与其对应舞动总次数的数学关系模型，可定量地对全省范围内的覆冰舞动总次数进行推算。

将78个台站的覆冰舞动总次数与其地形起伏度建立数学模型关系，二者的散点关系图和模型如图6所示。图中可见，当地形起伏度小于100 m时，地形起伏度与舞动总次数没有明显的关系，当起伏度逐渐增加时，覆冰舞动次数随之减小的趋势越来越明显，故可以考虑不对地形起伏度小于100 m的区域做订正，仅对地形起伏度大于100 m的区域做出定量订正。

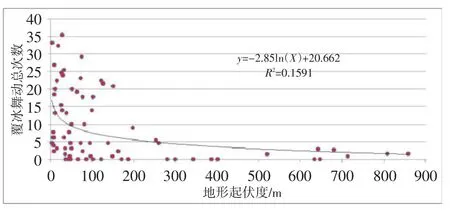
图6 覆冰舞动总次数与地形起伏度散点图Fig.6 Scatter plot of total galloping number and terrain

图7给出了当地形起伏度大于100 m时，与覆冰舞动次数的关系明显好转。采用对数关系模型，其复相关系数可达0.233 6，即相关系数为0.483。从关系模型可见，地形起伏度越大，覆冰舞动总次数越小，当地形起伏度达到约700 m时，覆冰舞动总次数基本为零，即山区发生舞动的可能性小。

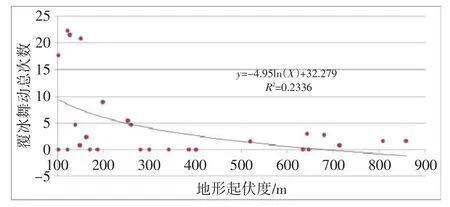
图7 覆冰舞动总次数与地形起伏度（大于100 m）散点图Fig.7 Scatter plot of total galloping number and terrain(more than 100 m)

最终确定对全省覆冰舞动总次数进行地形订正时，当地形起伏度小于100 m，直接使用气象因子建模的插值结果，当地形起伏度大于100 m，使用如下指数关系模型进行计算：

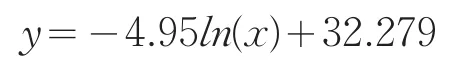
式中：y表示覆冰舞动总次数；x表示该点的地形起伏度。

3 气象地理模型确定舞动区域

利用地形影响因子所建立的定量订正的指数关系式，对湖北省的覆冰舞动总次数进行模拟，当地形起伏度小于100 m时，直接使用气象因子建模的插值结果，不订正。当地形起伏度大于100 m时，使用指数关系模型进行计算，模拟结果如图8所示。

图8中，湖北省覆冰舞动的大值区域位于鄂北的襄阳、枣阳、宜城至钟祥和荆门、随州、安陆至武汉周边区域，这与舞动的灾情实况完全吻合，在鄂西山区、鄂东山区、大洪山区和江汉平原东部的天门、潜江、仙桃地区，是覆冰舞动的少发区域。

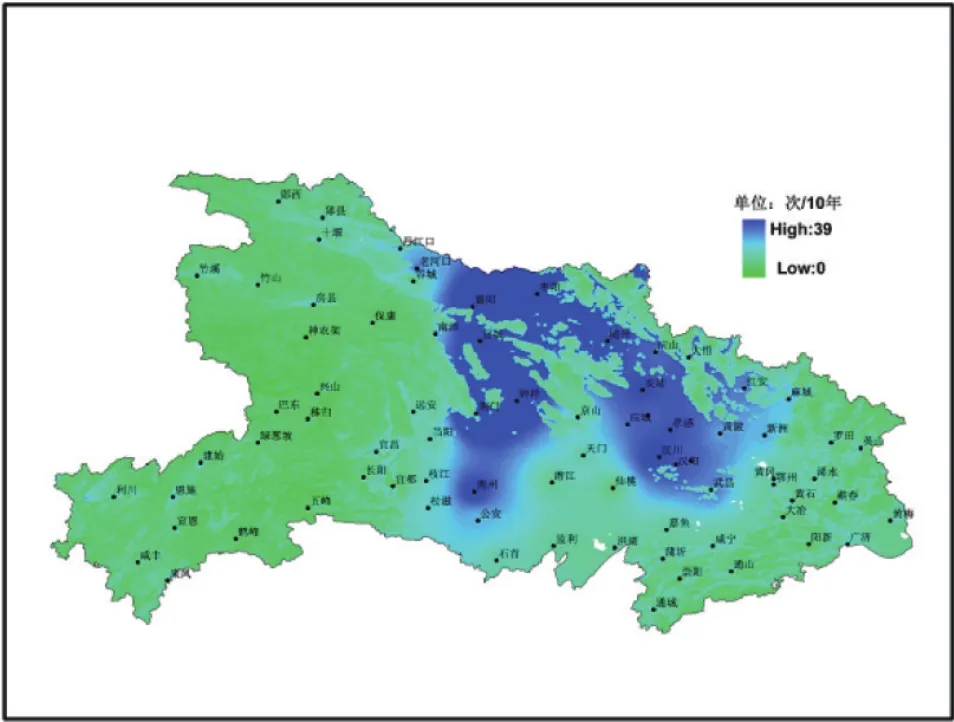
图8 湖北省覆冰舞动频次分布图（气象地理法模型）Fig.8 Frequency distribution of galloping in Hubei province(meteorological geography model)

4 结语

本文在统计和分析湖北输电线路历年来发生导线覆冰舞动情况的基础上，总结气象、地形特征规律，建立气象因子和地形起伏度与覆冰舞动地形定量关系组合模型，得到高精度的舞动频次区域分布。经运行经验验证，该舞动区域分布与实际情况相符，可用于指导舞动防治工作。

（References）

[1]胡毅.输电线路运行故障的分析与防治[J].高电压技术,2007,33(3):1-8.HU Yi.Analysis on operation faults of transmission lineand countermeasures[J].High VoltageEngineering,2007,33(3):1-8.

[2]龙立宏,胡毅,李景禄,等.输电线路冰害事故统计分析及防治措施研究[J].电力设备,2006,7(12):26-28.LONG Lihong,HU Yi,LI Jinglu,et al.Study on statistic analysis of icing faults on transmission line and its preventive measures[J].Electrical Equipment,2006,7(12):26-28.

[3]朱宽军,刘超群,任西春,等.特高压输电线路防舞动研究[J].高电压技术,2007,33(11):61-65.ZHU Kuanjun,LIU Chaoqun,REN Xichun,et al.Research on anti-galloping of UHV transmission line[J].High Voltage Engineering,2007,33(11):61-65.

[4]蒋兴良,周仿荣,王少华,等.输电导线覆冰舞动机理及防治措施[J].电力建设,2008,29(9):14-18.JIANG Xingliang,ZHOU Fangrong,WANG Shaohua,et al.Mechanism of icing-caused conductor galloping and its prevention[J].Electric Power Construction,2008,29(9):14-18.

[5]赵作利.输电线路导线舞动及其防治[J].高电压技术,2004,30(2):57-58.ZHAO Zuoli.Galloping of conductor of transmission line and precaution[J].High Voltage Engineering,2004,30(2):57-58.

[6]王少华.架空输电线路导线舞动及防治技术分析[J].高压电器,2010,46(12):63-67.WANG Shaohua.Analysis of conductor galloping phenomena on overhead transmission lines and anti-galloping techniques[J].High Voltage Apparatus,2010,46(12):63-67.

[7]王少华,蒋兴良,孙才新.输电线路导线舞动的国内外研究现状[J].高电压技术,2005,31(10):11-14.WANG Shaohua,JIANG Xingliang,SUN Caixin.Study status of conductor galloping on transmission line[J].High VoltageEngineering,2005,31(10):11-14.

[8]胡毅,胡建勋,刘庭.我国南方地区电网大范围覆冰灾害的特点分析与防治措施[J].电力设备,2008,9(6):1-4.HU Yi,HU Jianxun,LIU Ting.Analysis and countermeasures for large area icing accident on power grid in northern China[J],ElectricalEquipment,2008,9(6):1-4.

[9]涂明,张立春,朱宽军,等.输电线路舞动区域划分方法[J].电力建设,2011,32(4):26-28.TU Ming,ZHANG Lichun,ZHU Kuanjun,et al.Zoning method for galloping of transmission lines[J].Electric Power Construction,2011,32(4):26-28.

[10]马建国.湖北省电网舞动区域划分及防舞对策的研究[J].湖北电力,2002,26(4):100-101.MA Jianguo.Hubei power grid transmission line galloping region and anti-galloping method research[J].Hubei Electric Power,2002,26(4):100-101.

[11]丁锡广,陶文秋.减轻送电线路导线舞动灾害的措施[J].高电压技术,2004,30(2):54-55.DING Xiguang,TAO Wenqiu.Measures for reduction of damage caused by fluttered power transmission wires[J].High Voltage Engineering,2004,30(2):54-55.

[12]魏冲,潘少成,唐明贵,等.500 kV输电线路舞动分析及治理[J].电力建设,2011,32(4):22-25.WEI Chong,PAN Shaocheng,TANG Minggui,et al.Analysis and treatment of the galloping of 500 kV transmission line[J].Electric Power Construction,2011,32(4):22-25.