基于观测器的平台无陀螺姿态复合控制

，，，

1. 北京控制工程研究所，北京 100190 2. 北京空间飞行器总体设计部，北京 100094

未来天文观测、高分辨率对地观测等这类航天任务要求光学载荷实现亚角秒级的控制精度及极高的稳定度[1]。传统的航天器仅能实现0.01°的姿态控制精度[2]。而航天器星体平台的不稳定性将直接影响光学载荷高分辨率成像质量[3]，尤其是敏捷卫星，其成像积分时间内星体平台的微振动严重降低图像质量[4]。为隔离抑制星体平台微振动，提高光学载荷成像质量，研究人员在航天器平台和载荷之间引入具有主动指向控制Stewart平台[5-7]，构成超静卫星多级复合控制系统，并采用多级复合姿态控制技术提升载荷控制性能。在多级复合控制系统中，星体平台无陀螺或陀螺故障时，载荷敏感器与星体平台执行机构构成异位系统，需要研究在此配置时星体和载荷姿态复合控制问题。

研究人员设计了多种方法解决异位情况下航天器姿态复合控制问题。文献[8-9]分析了航天器引入Stewart平台时异位姿态控制的稳定性问题，提出了一种隔振与控制参数协同设计方法，其研究侧重于隔振参数的设计。文献[10]研究了基于Stewart平台的载荷与星体扰动隔振的动力学建模与姿态控制问题，其姿态控制只涉及到航天器星体平台控制,缺乏载荷二级控制。针对航天器平台和载荷的两级控制中缺乏足够的姿态信息，文献[11]采用观测器的思想估计平台姿态信息，在仅有Stewart平台作动器位移信息情况下，设计了基于观测器的Stewart平台正向运动学信息估计方法，实现了载荷位置跟踪控制。该方法中仅考虑了Stewart平台控制，缺乏星体一级的姿态控制。针对多输入多输出(Multiple Input Multiple Output,MIMO)系统控制，文献[12-13]通过构建连续滑模观测器实现Stewart平台作动器位移和速度信息估计，从而得到Stewart平台上平面的位姿信息(Stewart平台下平面固定)。当上平面信息可测量时，采用该方法可逆向估计下平面姿态信息。针对航天器姿态存在扰动情况，文献[14]给出航天器抗扰动滑模控制器的设计方法，为超静卫星多级姿态控制器的设计提供参考。文献[15-16]将噪声和干扰扩张为系统的状态，采用观测器估计扰动，实现扰动的估计及姿态稳定控制。

针对超静卫星载荷测量敏感器和平台执行机构非共基准时姿态异位控制问题，本文设计超螺旋(super-twisting)观测器，估计载荷和星体的相对角速度和星体平台角速度信息，实现星体和载荷的稳定控制。通过不同姿态控制模式校验观测器和控制器的正确性。数学仿真结果表明：在星体平台有陀螺时，载荷能够实现0.1″指向精度；在星体平台无陀螺时，采用观测器估计星体平台姿态并进行控制，载荷能够实现0.1″指向精度。所设计的方法能够保证星体平台无陀螺时整星和载荷的稳定控制，为工程实际姿态控制方案选择提供一种参考。

1 超静卫星动力学模型

超静卫星包括星体平台、挠性附件、Stewart隔振平台及载荷等部分。如图1所示，设I1为星体平台惯量，m1为星体平台质量；I2为Stewart平台惯量，m2为Stewart平台质量；I3为载荷惯量，m3为载荷质量。设Stewart平台第i(i=1，2，…，6)个杆li与星体平台和载荷的交点分别为ai、bi，且相对于星体平台质心和载荷质心的矢径分别为ρi和qi。星体平台与载荷通过Stewart平台相连接。设Stewart平台每个杆的刚度和阻尼系数分别为ki和ci。

定义xb=[rb，θb]为星体平台广义位移，rb、θb分别为星体平动和转动位移；xp=[rp，θp]为载荷广义位移，rp，θp分别为载荷平动和转动位移。令x=[xp，xb]T，建立星体平台/Stewart/载荷动力学模型为[17-18]：

式中：ddis系统扰动；系统参数M、K、C、U为：

式中：Ei为i×i的单位阵；fb=[Fb，τb]为星体平台的广义控制力，Fb为星体平台平动控制力，Fb≡0；ub为星体平台三轴姿态控制力矩；fp=[Fp，τp]为载荷广义控制力，Fp为载荷三轴平动控制力，τp为载荷三轴姿态控制力矩；r12为整星质心O1到Stewart平台下平面中心点O2的矢径。同理，参照式(4)可得到系统的阻尼阵C。

2 载荷控制策略

2.1 Super-twisting观测器设计

载荷敏感器与星体平台组成非共位系统进行姿态稳态控制时，需要准确获得星体平台姿态信息。在星体平台姿态信息无法直接测量得到时，需要设计状态观测器估计载荷和星体之间的相对姿态和角速度，从而得到星体平台姿态和角速度估计值。因此，需要在Stewart平台作动器关节空间设计状态观测器，估计作动器平动速度及星体平台姿态信息。常用的高增益观测器仅能实现平衡点状态时渐渐稳定估计，在作动器位移测量中含有周期扰动时，难以实现较高精度的估计。采用差分法估计作动器平动速度信息，将显著放大噪声，直接影响平台控制器性能。文中设计super-twisting观测器，估计作动器平动速度，实现星体平台姿态信息估计。

Stewart平台作动器运动学方程为：

由式(1)和式(5)可得作动器关节空间等效动力学方程为:

式中：

式中：矩阵AL21为非正定矩阵(在Jp，Jb为非负定时，可证明AL21为非正定)。同理，AL22为非正定矩阵。则在作动器关节空间设计的super-twisting观测器为：

定义Lyapunov函数V0为：

则有：

2.2 载荷控制器设计

在Stewart平台关节空间进行载荷控制器设计，实现载荷的稳定控制。由于Stewart平台各个支腿的刚度阻尼等系数存在一定的不确定

式中：f=AL21x1+AL22x2;g=BL21fp+BL22fb;ddis为扰动。

采用观测器式(8)可以得到x2的估计值。设计Stewart平台关节空间的滑模控制律为u=u0+u1,u0为系统的等效控制,u1为切换控制，定义如下：

式中：ε1、ε2为作动器的位移和速度控制误差；

系统的等效控制u0能够实现系统的稳定控制，但是容易引起执行机构的颤振现象，需要设计切换控制u1降低系统的颤振现象。

定义滑模面、twisting控制量以及切换控制u1为：

3 星体平台控制策略

采用观测器进行作动器平动速度估计，由式(5)Stewart平台运动学方程逆向求解，即可得到星体平台姿态信息估计值。

将系统动力学方程式(1)单独考虑星体平台动力学部分，其模型为：

定义星体平台相关控制量误差为：

式中：ξb=diag(ξb1，ξb2，…，ξb6)为误差广义力衰减系数，为正定矩阵。

设计的星体平台的控制器为:

星体平台控制器稳定性分析如下。

通过稳定性分析证明采用观测器式(8)能够实现Stewart平台作动器位移和速度估计误差收敛于平衡状态和控制器式(24)能够实现平台姿态和角速度误差收敛于平衡状态，保证星体平台控制稳定。

在考虑观测器式(8)和控制器式(21)以及系统动力学对象式(18)组成的闭环系统中，定义：

若满足以下条件：

则观测器式(8)和控制器式(23)及系统动力学对象式(20)组成的闭环系统是渐近稳定系统。

证明：

采用sb表示星体平台控制误差为：

考虑星体平台动力学式(18)和控制器式(21)，则式(24)为：

定义李雅普诺夫函数V1为：

V1沿系统闭环轨迹的微分为：

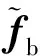
4 仿真校验

在超静卫星仿真平台进行姿态控制仿真，验证设计的观测器和控制器实现异位系统姿态控制的有效性。在考虑系统敏感器的测量噪声和航天器受到的高频扰动以及挠性振动情况下进行航天器姿态控制。仿真主要参数见表1。

表1 仿真参数Table 1 Parameters for simulation

根据表1仿真参数进行航天器姿态控制仿真，超静卫星平台扰动主要来自于控制力矩陀螺(Control Moment Gyros,CMGs)的高频扰动和翼板的挠性振动。以CMGs标称转速628.3 rad/s为例，其产生的高频扰动为100 Hz。同时设置挠性振动基频为0.05 Hz。则星体平台外部扰动设置为：

d=0.01[sin(2πft+φ1) sin(2πf+φ2)

sin(2πf+φ3)]T

式中：扰动力矩的频率f=[0.05，100] Hz。

为了全面验证设计的观测器和控制器的性能，进行3组姿态控制仿真，具体如下：

Case 1 采用差分法，super-twisting观测器两种方法对比作动器的速度估计精度。图2给出了采用两种方法的作动器平动速度估计精度对比结果。由图2可知，super-twisting观测器具有较高的估计精度，其作动器估计误差约在10-5m/s数量级。

Case 2 进行两种工况的姿态仿真：1)以载荷敏感器测量信息为输入，直接将载荷姿态和角速度信息反馈给星体平台控制器进行姿态控制；2)以观测器估计平台姿态和角速度信息为输入，进行星体平台姿态反馈控制。通过仿真结果对比验证异位控制姿态失稳现象以及观测器估计星体姿态角速度的必要性。图3给出了采用载荷测量反馈姿态控制结果，图4给出采用观测器估计星体平台姿态信息后进行姿态反馈控制。对比图3和图4可知，载荷测量信息直接反馈存在异位控制问题，导致星体平台姿态波动剧烈甚至失稳(如图3(b)所示)，随着时间的增加，载荷姿态也必将发散；而采用观测器能够准确估计星体平台姿态信息，实现平台和载荷的高精度控制(如图4所示)。其星体指向误差优于2″，载荷指向误差优于0.1″。

Case 3 在星体平台带刚性负载和挠性负载两种情况下进行姿态机动验证观测器和控制器的正确性。图5～图6分别给出了在刚性负载和挠性负载工况下进行90°大角度敏捷姿态机动过程中载荷和星体平台姿态控制误差对比。由图5敏捷机动姿态控制误差可知，观测器在敏捷机动过程中能够准确估计平台姿态信息，实现载荷的高精度稳定控制。在敏捷机动过程中，星体平台最大指向误差为200″，而载荷最大指向误差仅为6″。姿态仿真结果表明，在稳态控制时星体平台有陀螺刚性负载和挠性负载两种配置情况下载荷指向精度达到0.1″。由图5～图6可知在姿态机动结束进行稳定控制时，采用super-twisting观测器能够准确估计平台姿态，实现与星体平台有陀螺时载荷和星体同等量级的姿态控制精度。

5 结束语

针对超静卫星测量敏感器和执行机构分属于Stewart平台两端，载荷测量敏感器和星体平台执行机构异位姿态控制问题，设计了super-twisting观测器、载荷控制器和星体平台姿态控制器，解决了异位控制问题。通过3组姿态控制仿真验证了所提出的观测器和控制器的正确性，并得出如下结论：

1)载荷测量信息不能直接反馈平台进行姿态控制，易造成姿态失稳；

2)与差分法相比，super-twisting观测器能够实现Stewart平台作动器平动速度信息估计精度由10-4m/s提高到10-5m/s；

3)所设计的观测器和控制器能够实现载荷指向误差优于0.1″，该指标与平台有陀螺时同等

量级。所设计姿态复合控制方法为工程实际姿态控制方案选择提供一种参考。

References)

[1] LUIS M，FRANGK T，SATYA A. Line of sight stabilization of James Webb Space Telescope[C]//27th Annual AAS Guidance and Control Conference, February 5-9,2005. California: AAS，2005：1-15.

[2] 吴宏鑫，谈树萍. 航天器控制技术的现状和未来[J]. 空间控制技术与应用，2012，38(5)：1-7.

WU H X，TAN S P. Spacecraft control：present and future[J]. Aerospace Control and Application，2012，38(5)：1-7(in Chinese).

[3] 范斌，于起峰. 卫星平台运动对高分辨率光学遥感成像系统的影响分析[J]. 中国空间科学技术，2017，37(3)：86-92.

FAN B，YU Q F. Simulation analysis of platform vibration on image quality of satellite-based high-resolution optical system[J]. Chinese Spacecraft Science and Technology，2017，37(3)：86-92(in Chinese).

[4] 朱剑冰，张猛，王路远. 一种敏捷卫星积分时间的计算方法[J]. 中国空间科学技术，2017，37(1)：97-103.

ZHU J B，ZHANG M，WANG L Y. An integral time calculation method for agile satellite[J]. Chinese Spacecraft Science and Technology，2017，37(1)：97-103(in Chinese).

[5] 王有懿，汤亮，何英姿. 超静平台动力学建模与解耦控制[J]. 空间控制技术与应用，2016，42(4)：13 -18.

WANG Y Y，TANG L，HE Y Z. Dynamics modeling and decoupled control method of ultra-quiet platform[J]. Aerospace Control and Application，2016，42(4)：13-18(in Chinese).

[6] WU Y，YU K P，JIAO J，et al. Dynamic modeling and robust nonlinear control of a six-DOF active micro-vibration isolation manipulator with parameter uncertainties[J]. Mechanism and Machine Theory，2015，92：407-435.

[7] ZHANG J R，GUO Z X，ZHANG Y. Dynamics characteristics of vibration isolation platforms considering the joints of the struts[J]. Acta Astronautica，2016，126：120-137.

[8] 关新，陈守磊，崔颖慧,等. 超静敏捷卫星隔振与控制动力学耦合及协同设计方法[J]. 空间控制技术与应用，2015，41(1)：21-25.

GUAN X，CHEN S L，CUI Y H，et al. Dynamics coupling and integrated design in vibration isolation and attitude control design of ultra-quiet agile satellites[J]. Aerospace Control and Application，2015，41(1)：21-25(in Chinese).

[9] 关新，郑钢铁. 空间相机隔振与姿态控制一体化设计[J]. 宇航学报，2013，34(2)：214-221.

GUAN X，ZHENG G T. Integrated design of space telescope vibration isolation and attitude control[J]. Journal of Astronaitics，2013，34(2)：214-221(in Chinese).

[10] ZHANG Y，ZHANG J R. The imaging stability enhancement of optical payload using multiple vibration isolation platforms[J]. Journal of Vibration and Control，2013，21(9)：1-18.

[11] CHEN S H，FU L C. Observer-based backsteping control of a 6-DOF parallel hydraulic manipulator[J]. Control Engineering Practice，2015，36：100-112.

[12] LEONID F，ARIE L，JORGE D. Observation and identification via high order sliding modes[J]. Modern Sliding Mode Control Theory，2008，35：293-319.

[13] KUMAR P R，ASIF B，BAND B Y. Smooth integral sliding mode controller for the position control of Stewart platform[J]. ISA Transactions，2015，58: 543-551.

[14] 杜辉，郝金华，邢林峰. 一类带液体晃动的航天器滑模姿态控制器的设计[J]. 中国空间科学技术，2015，35(2)：63-69.

DU H，HAO J H，XING L F. Sidling-mode attitude controller design for a kind of spacecraft with fuel slosh[J]. Chinese Spacecraft Science and Technology，2015，35(2)：63-69(in Chinese).

[15] 袁国平，史小平，李隆. 基于扩张状态观测器的航天器自适应姿态控制[J]. 中国空间科学技术，2011，31(5)：9-17.

YUAN G P，SHI X P，LI L. Adaptive controller for spacecraft attitude maneuver based on extended state observer [J]. Chinese Spacecraft Science and Technology，2011，31(5)：9-17(in Chinese).

[16] 王亮，刘向东，盛永智，等. 基于扰动观测器的指数时变滑模再入姿态控制[J]. 中国空间科学技术，2013，33(4)：31-39.

WANG L，LIU X D，SHENG Y Z，et al. Disturbance observer based exponential time-varying sliding mode for the re-entry attitude control [J]. Chinese Spacecraft Science and Technology，2013，33(4)：31-39(in Chinese).

[17] JIANG H Z，HE J F，TONG Z Z，et al. Dynamics isotropic design for modified Gough-Stewart platforms lying on a pair of circular hyperboloids[J]. Mechanism and Machine Theory，2011，46：1301-1315.

[18] JIANG H Z，TONG Z Z，HE J F，et al. Dynamics isotropic design of a class of Gough-Stewart parallel manipulator lying on a circular hyperboloid of a sheet [J]. Mechanism and Machine Theory，2011，46：358-374.

[19] BHAT S P. BERSTEIN D S. Geometric homogeneity with applications to finite time stability[J]. Journal of Math control Signals Systems，2005，17：101-127.