基于ABAQUS软件的挡土结构土压力分析
谢治华
(湖南润丰源水利技术服务咨询有限公司 长沙市 410007)
引 言
在水利、土木交通等工程中,经常会遇到修建挡土结构的问题,它是用来支撑天然或人工斜坡不致坍塌、以保持土体稳定性的建筑物。无论采用哪种形式的挡土结构,都要承受来自墙后填土的侧向压力(也称土压力)[1]。因此,土压力是设计挡土结构断面及验算其稳定性的主要荷载。
岩土工程分析中,由于岩土本构关系的非线性、荷载及边界条件的负责性,用解析方法求解难度很大、通常需要采用数值方法进行计算,数值分析结果是岩土工程师对问题进行判断的重要依据之一。有限元法可以在计算中真实的反映材料的非线性本构关系,能够实现各种复杂边界条件,是岩土工程数值分析中最常见、也是最强有力的分析方法。ABAQUS是一款功能强大的通用有限元软件,包含十分丰富的材料模型、单元模式、荷载及边界条件,能够求解静力、动力等多种问题,具备处理填土或开挖等岩土工程中的特定问题的能力,尤其是在求解高度非线性问题方面的能力十分优异,对岩土工程有较强的适用性。
本文采用ABAQUS软件建立挡土结构有限元计算模型,通过设置不同的荷载条件,得到挡土结构的土压力分布规律。计算结果表明,采用本文方法可以更好地指导挡土结构的设计,亦为类似工程提供设计参考。
1 ABAQUS软件介绍
ABAQUS[2~3]是由美国HKS公司开发的非线性有限元分析软件,是世界上先进的大型通用有限元分析软件之一。它在材料、几何与接触非线性方面的分析能力居世界领先水平,并以高求解效率和高计算精度在工程界和学术界赢得了声誉和信赖,被誉为有限元软件中的贵族,广泛应用于科学研究与工程计算中。在岩土工程方面,ABAQUS广泛的应用在边坡稳定分析、固结、渗流、蠕变、基坑开挖和地下开挖等复杂岩土力学问题的研究和计算中。
2 土压力理论
作用在挡土构筑物上的土压力计算是一个比较复杂的问题,影响因素也很多,除与土的力学性质有关外,还和墙体的位移方向、位移量、土体与结构物之间的相互关系以及挡土结构物类型有关。在影响土压力的诸多因素中,墙体位移条件是最主要的因素,墙体位移的方向和位移量决定着产生的土压力性质和土压力大小。就一般来说,挡土结构后的土压力可能有三种,即静止土压力、主动土压力和被动土压力。三种土压力的定义和计算方法各不相同。
(1)静止土压力。
在墙后填土的作用下,当挡土结构完全没有侧向位移、偏转和自身弯曲时,作用在其上的土压力称为静止土压力。
静止土压力的计算常根据墙后某点竖向应力σ′v的大小估计水平应力σ′h,水平应力的分布图形面积即为静止土压力。

式中K0——静止土压力系数,正常固结土可根据图档有效摩擦角 估计:

(2)主动土压力。
当挡土结构在外力的作用下产生离开填土方向移动或转动时,墙后土体达到主动极限平衡状态,有下滑的趋势,此时,作用在墙上的土压力达到最小值,称为主动土压力。
主动土压力的计算理论主要有朗肯理论和库伦理论。朗肯理论假设挡土墙墙背竖直、光滑、填土面水平、其根据墙后某点的极限平衡条件,得到主动土压力 σ′a为:
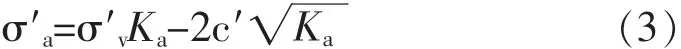
式中 Ka=tan2(45°-φ′/2)是主动土压力系数,土体的c′有效黏聚力,其余参数意义同前。
库伦土压力理论从破坏楔体的整体平衡出发,假设破坏面为平面,给出的主动土压力系数为:

式中α——填土倾角;
β——墙背倾角;
δ——墙与土之间的摩擦角,如无实验系数,可假设为 2φ′/3。
(3)被动土压力。
当挡土结构在外力的作用下向着填土方向移动或转动时,墙后土体达到被动极限平衡状态,有上滑的趋势,此时,作用在墙上的土压力达到最大值,称为动土压力。
按照朗肯理论,被动土压力σ′p为:
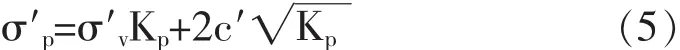
库伦理论给出的被动土压力系数为:

3 计算实例
如图1所示,有一个高3 m的混凝土重力式挡土墙,弹性模量E=20 GPa,泊松比v=0.2。墙后为干砂,填土表面作用荷载7 kPa,弹性模量E=50 MPa,泊松比 v=0.3,凝聚力 c′=0 kPa,摩擦角 φ′=37°,剪胀角 ψ=10°,重度 γ=17KN/m3,假设挡土墙静止不动、绕墙趾向左及向右旋转,求墙后土压力。

图1 模型示意图
按照ABAQUS软件的一般计算流程对以上模型进行分析,即:创建部件—定义材料及截面特征—装配部件—定义分析步—定义接触—定义荷载、边界—划分网格—提交任务进行分析—结果后处理。模型网格划分见图2,采用在定义荷载、边界中对模型的受力进行区分,分别分析挡土墙静止不动、绕墙趾向左及向右旋转三种工况挡墙墙后的土压力。为了区分对待,将绕墙向左和向右的位移(即B点出的位移)分别定义为0.003 m和0.01 m。图3~图5为以上三种工况下模型的荷载分布。
图6~图8为挡土墙的位移矢量图,从图7和图8中可以看出挡土墙都沿A点发生了旋转,且B点的位移值都为输入值,计算基本达到了预期效果。
(1)静止土压力的分布。
将挡土墙静止不动时的加载结束时的土压力分布绘制于图9,此时由于墙体保持不动,土压力可以认为是静止土压力,由于填土在重力荷载下未破坏,处于弹性区域,侧向土压力系数可用v/(1-v)估算,计算表明理论值与有限元计算结果非常吻合。

图2 模型整体网格示意图

图3 挡土墙静止不动荷载分布图
图4 挡土墙绕墙趾左旋荷载分布图

图5 挡土墙绕墙趾右旋荷载分布图

图6 静止不动挡土墙位移矢量图
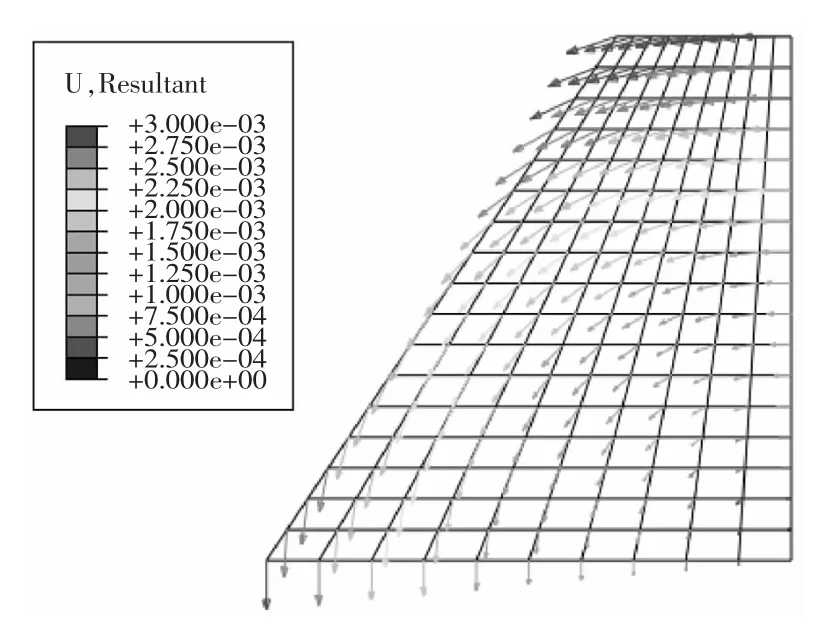
图7 绕墙趾左旋挡土墙位移矢量图

图8 绕墙趾右旋挡土墙位移矢量图
(2)主动土压力分布。
挡土墙绕墙趾左旋转移动的土压力分布见图10、墙后填土的塑性应变分布图见图11。由图可见,本算例中当墙顶位移达到1%的墙高后,墙后的大部分区域已经处于主动极限平衡状态,土压力减小为主动土压力。由图还可以看出,在墙趾附件,墙体的位移还不足以使土体达到主动极限平衡状态,土压力介于静止土压力和主动土压力之间。
(3)被动土压力分布。
将挡土墙绕墙趾右旋转计算结束后的土压力与朗肯被动土压力理论值对比于图12,由图可见,对比主动土压力分布,被动土压力的发挥需要挡土墙发生更大的位移,本算例中墙后填土还未完全达到被动极限平衡状态(见图13墙后土体的塑性分布),土压力呈曲线分布。

图9 静止土压力分布图
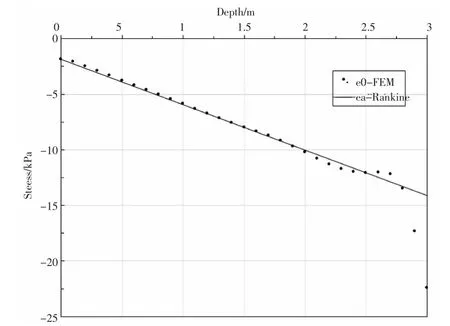
图10 主动土压力分布图

图11 墙后填土的塑性应变分布图
4 结论与建议
ABAQS软件将有限元分析、计算机图形学和优化技术相结合,具备较为完善的分析功能。本文运用ABAQUS软件对某一重力式挡墙后的土压力进行了数值求解,并将有限元分析结果与理论计算值进行对比,取得了较好的效果,得出以下结论和建议:
(1)在用ABAQUS软件建立计算的时候,无需将挡土结构与土体建立成一个整体,采用接触可以很好的模拟挡土结构与土体的相互作用。概念清楚、操作简单、结果可靠。

图12 被动土压力分布图

图13 墙后填土的塑性应变分布图
(2)通过本文可以很清楚的区分作用在挡土结构上的静止土压力、主动土压力、被动土压力的概念、受力状态及分布形式。
(3)为了达到分析效果,本次算例通过给定墙体位移方向及位移量来分析墙后填土的受力状态。然而,实际工程中不少挡土结构的位移量并未达到土体发生主动或被动极限平衡状态的位移量(见图12),这种情况下任意位移下的土压力计算比较复杂,采用理论方法不一定与实际情况相符合。
(4)通过有限元法可以确定挡土结构位移量与土压力大小、分布状态之间的定量关系。可为实际工程中一些重要挡土结构的设计提供分析依据,指导设计,使设计成果更加科学合理。
[1]陈仲颐,周景星,王洪瑾.土力学[M].北京:清华大学出版社,1992.
[2]庄茁,张帆,岑松,等.ABAQUS非线性有限元分析与实例[M].北京:科学出版社,2005.
[3]ABAQUS.Standard User's Manual[M].Hibbitte Karlsson&Sorenson INC,2002:26-78.

