强耦合薛定谔系统的多辛整体保能量方法

袭春晓，孙建强，闫静叶

(海南大学 信息科学技术学院，海南 海口 570228)

强耦合薛定谔系统的多辛整体保能量方法

袭春晓，孙建强，闫静叶

(海南大学 信息科学技术学院，海南 海口 570228)

首先基于二阶平均向量场方法和拟谱方法构造了强耦合薛定谔系统的多辛整体保能量格式，然后利用多辛整体保能量格式数值模拟系统孤立波的演化行为，最后数值结果表明多辛整体保能量格式可以较好地模拟强耦合薛定谔系统孤立波的演化行为，还可以精确保持系统的整体能量守恒特性.

多辛整体保能量方法； 平均向量场方法； 强耦合薛定谔系统

强耦合薛定谔系统在非线性光学和等离子体物理学中具有重要的意义,分析和求解强耦合薛定谔系统已成为数学和物理学科中非线性问题的研究热点.考虑如下强耦合薛定谔系统[1-3]

(1)

近年来,一些能够保持多辛守恒的多辛算法被陆续提出,如多辛Runge-Kutta方法,多辛Preissman格式,多辛Euler box格式和多辛谱方法等[4-9],在求解非线性孤立子偏微分方程中发挥重要作用,并已利用相应的多辛算法对强耦合薛定谔系统进行求解.但是这些多辛算法只能近似保持强耦合薛定谔系统的整体能量.王雨顺[9]等人利用二阶平均向量场方法[10-11]的思想提出了多辛整体保能量方法，该方法不仅能够很好地模拟多辛结构的薛定谔方程和KdV方程,而且还能够精确地保持方程的整体能量守恒特性,同时已应用平均向量场方法于辛结构的哈密尔顿系统的计算[12-13].笔者利用多辛整体保能量方法求解具有多辛结构的强耦合薛定谔系统.

1 强耦合薛定谔系统的多辛整体保能量格式

设u=p(x,t)+iq(x,t),v=c(x,t)+id(x,t),引入变量a,b,e,f，并且满足px=a,qx=b,cx=e,dx=f,则式(1)可表示为如下多辛结构

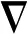
(2)

其中,

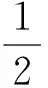
z=(p,q,a,b,c,d,e,f)T,

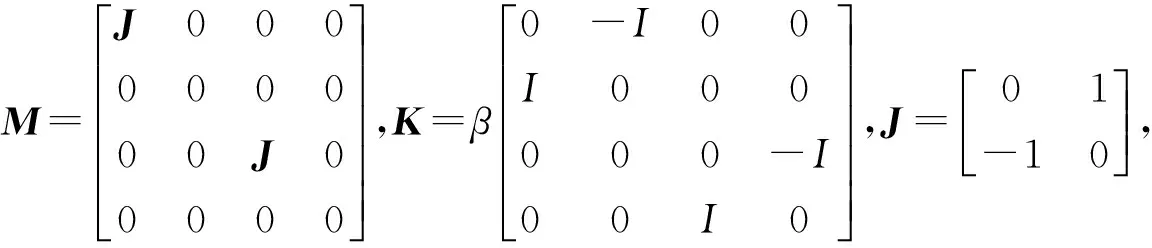
其中，0和I分别为二阶零矩阵和单位矩阵,M和K为反对称矩阵,S∶R8→R是一个光滑函数.式(2)满足如下的多辛守恒律

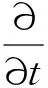
(3)

(4)

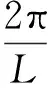
(5)

插值算子IN在配置点xj满足

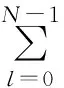
(6)

设u=(u0,u1,…，uN-1)T,定义

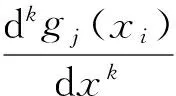
(7)

称Dk为阶微分矩阵.通过计算可以得到

(8)

D1是如下的一阶反对称谱矩阵

(9)

式(2)在空间方向用谱方法离散后,可转化为如下方程

(10)

其中，z=(PT,QT,AT,BT,CT,DT,ET,FT)T,P=(p0,…，pj,…，pN-1)T，j=0,1,…，N-1.

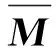
(11)

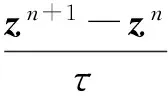
离散格式(11)经过化简后,等价于如下格式

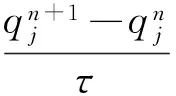
(12)

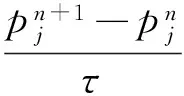
(13)

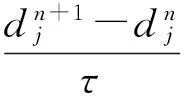
(14)

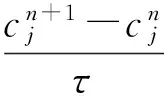
(15)

其中,j=0,1,2,…，N-1. 用(RE)n表示tn时刻的局部能量剩余误差,格式(11)的局部能量剩余误差为

(16)

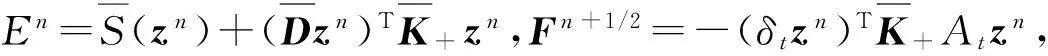
15个肺结核病例CT检查均使用日本原装东芝Aquilion16排32层螺旋CT，患者取仰卧位，头先进的方式进入，让患者双臂上举抱头，扫描参数常规平扫为容积扫描，然后5mm肺窗、纵隔窗重建，扫描条件：120KV，自动毫安秒技术，尽量减少辐身剂量。

系统(1)在tn时刻的离散的整体能量

εn=hEn.

(17)

定理1 格式(11)满足离散整体能量守恒

εn+1=εn.

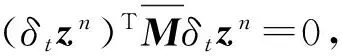
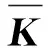
(18)

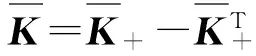
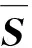
(19)

根据交换律和离散Leibniz定律

δt(z·y)n=δtzn·Atyn+Atzn·δtyn,

则有

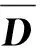
(20)

从式(19)和(20)可以得到

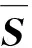
证毕.

2 数值模拟

定义强耦合薛定谔系统在tn时刻的整体误差能量为

RE(tn)=|εn-ε0|.

(21)

设强耦合薛定谔系统的初始条件为

(22)

2.1数值模拟1取r1=r2=1,D0=20,V0=1，Γ=0.

图1 α1=1.5,α2=1时|u|的数值解 图2 α1=1.5,α2=1时|u|的数值解

图3 α1=1.5,α2=1时|u|数值解的整体能量误差变化

从图1～2可知,整体保能量格式能够很好地模拟系统(1)的孤立波的演化行为,数值结果与文献[1]的结果一致.图3表示系统(1)的能量误差随时间的变化,能量误差很小可忽略不计.因此,保能量格式(11)能够很好地保持系统的能量守恒特性.

2.2 数值模拟 2 取r1=r0=1,D0=20,V0=1,α1=1.5,α2=1.

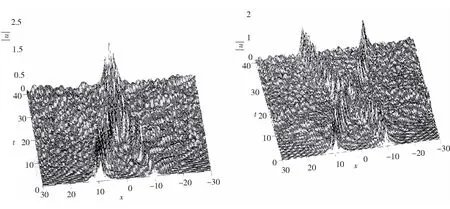
图4 Γ=0.5时|u|的数值解 图5 Γ=0.5时|u|的数值解

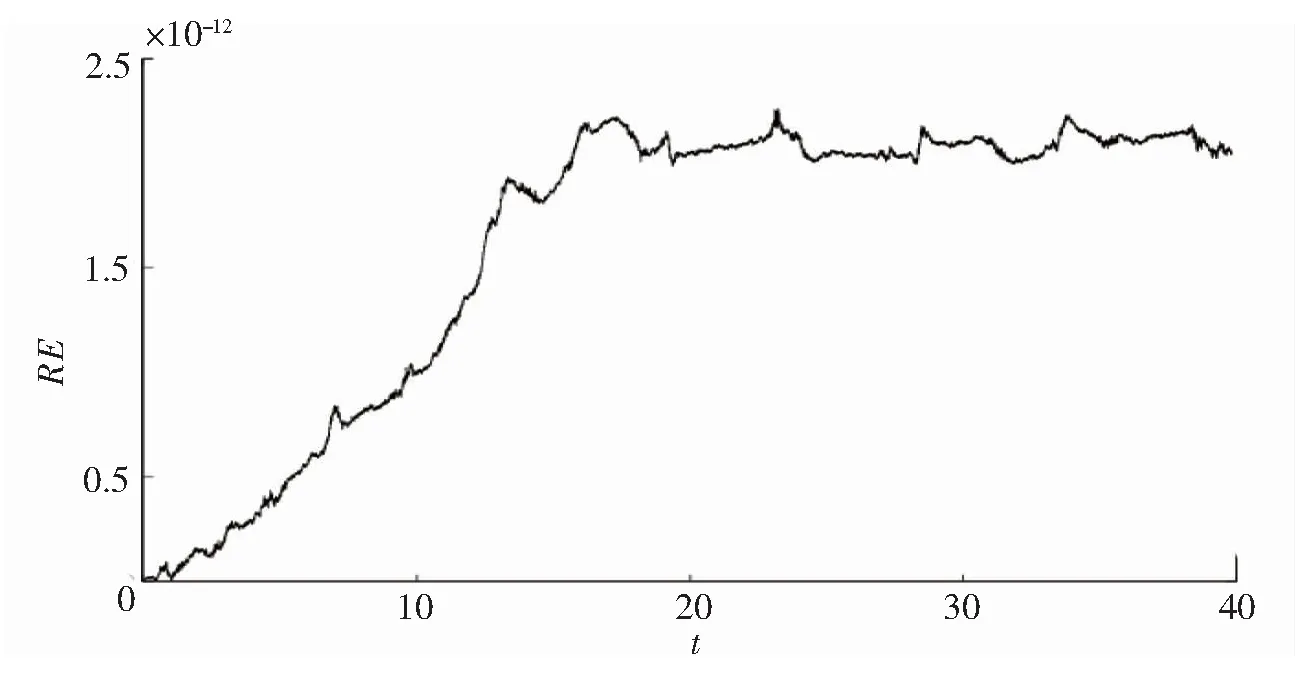
图6 Γ=0.5时|u|的数值解的整体能量误差变化

从图4～5可知,整体保能量格式(11)能够很好地模拟系统(1)的孤立波的演化行为.图6表示方程组(1)的能量误差随时间的变化,能量误差很小可忽略不计.从图4～6可知,整体保能量格式同样能够有效地模拟系统孤立波的行为且保持系统的离散能量守恒特性.

综上所述，整体保能量格式(11)能在不同的参数条件下很好地模拟强耦合薛定谔系统孤立波的演化行为,并精确地保持系统的离散能量守恒特性.

3 小 结

首先利用二阶平均向量场方法和拟谱方法构造了强耦合薛定谔系统的多辛整体保能量格式，然后利用多辛整体保能量守恒格式对强耦合薛定谔系统进行数值模拟，最后数值结果表明强耦合薛定谔系统多辛整体保能量格式可以很好地模拟孤立波的演化行为,还可以精确地保持系统离散能量守恒特性.因此在整体保能量守恒方面,相比已有的经典的多辛格式,本文所构造的强耦合薛定谔系统的多辛整体保能量格式具有一定的优越性.

[1]CaiJX.MultisymplecticschemesforstronglycoupledSchrdingersystem[J].Appl.Math.andComput, 2010,216:2 417-2 429.

[2]TaoYS,HeJS,DorsezianK.Deformedsolition,breather,androguewavesolutionofaninhomogeneousnonlinearSchrdingerequation[J].Chin.Phys.B, 2013, 22 (7):237-241.

[3]ZhangH,SongSH,ZhouWE.Multi-symplecticmethodforthecoupledSchrödinger-Kdvequation[J].Chin.Phys.B,2014, 23 (8) : 1-7.

[4]LiHC,SunJQ,QinMZ.Newexplicitmulti-symplecticschemefornonlinearwaveequation[J].Appl.Math.Mech-Engl,2014, 35 (3) : 369-380.

[5]WangY,HongJL.Multi-symplecticalgorithmsforHamiltonianpartialdifferentialequations[J].Commun.Appl.Math.Comput, 2013, 27 : 163-230.

[6] 王雨顺, 洪佳林. 哈密尔顿偏微分方程多辛算法 [J]. 应用数学与计算数学, 2013, 27 (2) : 163-230.

[7]WangJ.Anoteonmulti-symplecticFourierpseudospectraldiscretizationforthenonlinearSchrödingerequation[J].Appl.Math.AndComput, 2007, 191 : 31-41.

[8]ChenJB,QinMZ.Multi-symplecticFourierpseudospectralmethodforthenonlinearSchrödingerequation[J].Electr.Numer.Anal, 2001, 12 : 193-204.

[9]GongYZ,CaiJX,WangYS.Somenewstructure-preservingalgorithmsforgeneralmulti-symplecticformulationsofHamitonianPDEs[J].Comput.Phys, 2014, 279: 80-102.

[10]QuispelGRW,MclarenDI.Anewclassofenergy-preservingnumericalintegrationmethods[EB/OL].[2017-04-20].https://www.researchgate.net/profile/G_Quispel/publication/231087309_A_new_class_of_energy-preserving_numerical_integration_methods/links/0fcfd50d3d55e0c330000000/A-new-class-of-energy-preserving-numerical-integration-methods.pdf.

[11]CelledoniE,GrimmV,MclachlanRI,etal.Preservingenergyresp.DissipationinnumericalPDEsusingthe“AverageVectorField”method. [J].Comput.Phys, 2012, 231 : 6 770-6 789.

[12] 李昊辰, 孙建强, 骆思宇. 非线性薛定谔方程的平均向量场方法 [J]. 计算数学, 2013, 35 (1) : 60-66.

[13]JiangCL,SunJQ,HeXF,etal.Highorderenergy-preservingmethodofthe“Good”Boussinesqequation[J].NumericalMathematics:TheoryMethodandApplication, 2016, 9 (1) : 111-122.

GlobalEnergy-PreservingMethodforStronglyCoupledSchrödingerSystem

Xi Chunxiao, Sun Jianqiang, Yan Jingye

(College of Information Science and Technology, Hainan University, Haikou 570228, China)

Based on the second order average vector field method and the Fourier pseudo method, the multi-symplectic global energy-preserving scheme for strongly coupled Schrödinger system was constructed. And the multi-symplectic global energy-preserving scheme data was used to simulate the evolution behaviors of the system. The results showed that the global energy-preserving scheme can simulate the wave evolution behaviors of strongly coupled Schrödinger system in a long time and preserve the global energy conservation very well.

multi-symplectic global energy-preserving method; average vector field method; strongly coupled Schrödinger system

2017-05-29

国家自然科学基金项目(11561018)

袭春晓(1994-)，女，山东济南人，海南大学2016级硕士研究生，研究方向：微分方程的数值解法，E-mail： 864768487@qq.com

孙建强(1971-)，男，湖南双峰人，教授，研究方向：微分方程的数值解法，E-mail：sunjq123@qq.com

1004-1729(2017)04-0310-06

O 241.8

ADOl10.15886/j.cnki.hdxbzkb.2017.0048