基于隶属度修正的加权马尔可夫链的降水预测
,
(1.河北水利电力学院 水利工程系,河北 沧州 061001;2.宁夏水利科学研究院,银川 750021)
基于隶属度修正的加权马尔可夫链的降水预测
苗正伟1,徐利岗2
(1.河北水利电力学院 水利工程系,河北 沧州 061001;2.宁夏水利科学研究院,银川 750021)
应用Fisher最优分割法将榆林地区1951—2015年的年降水序列划分为9个状态,采用规范化的各阶自相关系数为权重,建立了加权马尔可夫链模型。以属于同一状态的所有降水量的均值作为聚类中心,应用模糊C均值聚类(Fuzzy C-Means,FCM)算法中的隶属函数计算隶属度,以隶属度向量作为预测时的初始状态向量。该模型逐年预测了榆林市2006—2015年的降水状态,结果全部与实际情况一致。基于马尔可夫链的预测结果,采用模糊集中的级别特征值理论分别预测了2006—2015年的降水量,所有预测结果的相对误差都在10%以内,初步表明基于隶属度修正的加权马尔可夫链模型是合理可行的。
降水预测;隶属度;加权马尔可夫链;模糊集;榆林
1 研究背景
如何科学划分降水状态,是用加权马尔可夫链进行预测的重要问题,最常用的方法是均值-标准差法,但该方法在参数选择上主观性较强,尤其当标准差较大时,不同参数值会使状态区间范围变化幅度很大。Fisher最优分割法不但能使状态划分更客观合理,而且还能为分类数的选择提供数学依据。
此外,传统的马尔可夫链是将某时刻所处的实际状态作为单位向量,然后以该单位向量为初始向量进行预测[1],这种处理方法明显与实际情况不符:设某时刻的降水量处于偏丰范围的上限,此时它已很接近丰水年的水平,而且降水状态本就没有具体的数值范围来绝对划分,这种情况下若毫不考虑丰水状态的概率,是不合理的。
鉴于此,本文利用模糊C均值(Fuzzy C-Means,FCM)算法中的隶属函数,赋予每个年降水量属于各状态的隶属度,从而使用隶属度向量作为初始向量进行预测。
2 基本原理
2.1 Fisher最优分割法
Fisher最优分割法是在保持序列顺序不变的前提下[2],以类内离差平方和最小为目标的一种聚类算法。基本步骤如下:
(1) 对于数据为一维变量的序列X,设某分法中某一类包含的数据为{Xi,Xi+1,…,Xj},则定义该类的类直径为
(1)
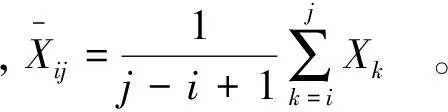
式中:i,j为数据在原序列中的序号。
(2) 用f(n,k)表示将n个有序样品分为k类的某种分法,该分法的目标函数定义为

(2)
式中:it表示第t类中第一个数据的序号;it+1-1表示第t类中最后一个数据的序号。
最优分割要求目标函数最小,即:L[p(n,k)]=min{L[f(n,k)]}。
(3) 可以证明,将n个有序数据分成k类的最优分割,一定是先将前j-1个数据最优分割为k-1类,剩下的数据自成一类,即[3]
L[p(n,k)]=min{L[p(j-1,k-1)]}+D(j,n),
k≤j≤n。
(3)
可见最优分割算法的重点就是上述递推公式,须编程实现。
(4) 分类数的确定。在分类数不能提前确定时,可以通过L[p(n,k)]-k关系图,以某k值时曲线是否有明显转折及大于某k值时曲线是否变得很平缓为标准来选择合理的分类数。
2.2 加权马尔可夫链模型
关于加权马尔可夫链的基本原理和建模步骤参见文献[4]至文献[6]。
2.3 模糊C均值算法中的隶属函数
用模糊集理论来处理聚类问题,即为模糊聚类分析。在模糊聚类算法中,应用最广泛且较成功的是FCM算法,该算法中隶属函数的规定如下[7-8]:
∀j=1,2,…,N;
(4)
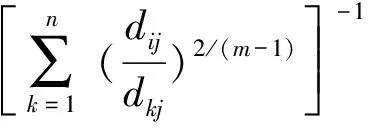
(5)
式中:uij表示第j个样本数据对第i个聚类中心的隶属度;dij=‖ci-Xj‖为第i个聚类中心与第j个样本数据间的欧氏距离;ci为第i个模糊聚类的聚类中心;m是一个模糊加权指数,通常取为2[9]。
2.4 模糊集理论的级别特征值
由下式定义级别特征值[10-11]h,即
(6)

式中:k为状态;S为状态空间;φk为状态k的权;pk,pr分别为状态k,r的预测概率;θ为最大概率作用系数。
降水量预测值Xk由下式给出,即
(7)
式中:Uk,Dk分别为状态k所在区间的上下限;h为级别特征值。
3 预测模型的建立步骤
(1) 应用Fisher最优分割法划分降水序列的状态。
(2) 以各状态中所有降水量的算术平均值作为聚类中心,采用式(5)计算降水量对于每个状态的隶属度。
(3) 权重定义为
(8)
式中:k表示步长;ωk表示步长为k的转移概率的权重;b为按预测需要计算到的最大步长;rk表示第k阶自相关系数,其表达式为
(9)

(4) 计算转移矩阵:因降水因素极其复杂且规律性不明显,所以很难准确给出降水状态的转移概率,当数据系列足够长时,可用转移频率近似代替转移概率,步长为1的转移频率为
(10)
式中fij表示年降水量从状态i一步转移到j的频次。与式(10)同理,由样本序列统计各状态间各步长的转移频率,各步长的转移频率构成相应步长的转移矩阵,它决定了降水状态转移的概率法则。
(5) 以距离待预测年份步长为k的年降水量的隶属度为初始向量,结合相应的k步转移矩阵和k阶权重,即可得到基于步长k的降水数据预测出的概率向量Tk,k=1,2,…,b。
(6) 将各步长的概率向量求和,则有
(11)
向量T中各元素的最大值所对应的状态即为预测状态。
(7) 应用级别特征值公式计算降水量的预测值。
4 模型在榆林市年降水量预测中的应用
4.1 研究区概况
榆林市位于陕西省北部,位置在107°28′E—111°15′E,36°57′N—39°35′N,地势由西部向东南倾斜,西南部平均海拔1 600~1 800 m,其他各地平均海拔1 000~1 200 m。地貌分为风沙滩区和黄土丘陵沟壑区两大类。气候为典型的温带大陆性季风气候,区域多年平均相对湿度57.5%,年平均气温为10.7 ℃,极端最高气温为38.9 ℃,极端最低气温为-24 ℃,气象灾害多发。全市多年平均降水量为397.7 mm,历年最大年降水量为849.6 mm,最小年降水量为108.6 mm;降水量年内分配不均,6—9月份的降水量占全年的75%,降水变差系数范围为0.23~0.31;多年平均水面蒸发量为1 211 mm,多年平均干旱指数为3.0[12]。
4.2 数据来源
从“中国气象数据网”下载了榆林市1951—2015年的逐月降水量,并将之整理为年降水序列,结果如表1。
表1榆林市1951—2015年降水量分类及聚类中心
Table1ClassificationofannualprecipitationinYulincityfrom1951to2015andcorrespondingclustercenters

状态聚类中心/mm降水量区间/mm1159.1x<203.902271.5203.90≤x<290.853315.9290.85≤x<339.304359.0339.30≤x<387.255414.0387.25≤x<432.806448.4432.80≤x<474.407492.7474.40≤x<512.858552.3512.85≤x<632.059690.5x≥632.05
4.3 隶属度修正的加权马尔可夫链模型的建立及应用
(1) 首先将数据按从小到大的顺序排列[13],然后根据Fisher最优分割的基本原理编制MATLAB程序进行计算。因序列长度为65 a,类直径及各目标函数值的计算结果数据较多,限于篇幅,故略去,只给出65个数据k类最优分割的目标函数L[p(65,k)]与分类数k的关系曲线,如图1所示。

图1 榆林市L[p(65,k)]-k曲线Fig.1 The L[p(65,k)]-k curve in Yulin city
普遍把降水状态均分为5类,但从图1可以看出k=5处曲线还有明显转折;在k=6~8处尽管转折不明显,但曲线下降的趋势还是比较大;而在k=9处开始曲线变得很平缓,逐渐逼近横坐标轴,说明分类数超过9之后,目标函数值减小趋势变得很缓慢,换言之,分类大于9的情况与分成9类相比并无明显意义。因此,本文将降水序列划分为9类,并以各状态中所有降水量的算术平均值作为聚类中心,结果如表1。
(2)按表1确定榆林市1951—2015年各年降水量的状态,结果如表2所示。
(3) 取模糊加权指数m=1.8,根据式(5)计算各年降水量的隶属度,因数据量为9×65=585,限于篇幅,此处不详述。
(4) 选择转移矩阵和自相关系数的最大步长并计算各阶权重:转移矩阵最大步长普遍根据经验确定,并无严谨理论依据。本文经多次试验后确定最大步长b=22。计算1—22阶自相关系数和权重,结果如表3所示。

表2 榆林市1951—2015年降水量及其状态Table 2 Annual precipitation and states inYulin city from 1951 to 2015
(5) 对降水状态序列进行统计计算,得步长为1—22的转移概率矩阵,因篇幅限制,只列出P(1)和P(22)示意,即:

(6) 首先根据1984—2005年的年降水数据预测2006年的年降水状态。
1984—2005年降水量的隶属度如表4。
求2005年的隶属度向量u2005与一步转移矩阵P(1)的积,然后再用步长为1的规范化自相关系数ω1进行加权,即得到基于步长为1的转移矩阵的预测结果T1,即:T1=u2005·P(1)·ω1;
求2004年的隶属度向量u2004与两步转移矩阵P(2)的积,然后再用步长为2的规范化自相关系数ω2进行加权,即得到基于步长为2的转移矩阵的预测结果T2,即:T2=u2004·P(2)·ω2;
同理:求年份为t的隶属度向量ut与k步转移矩阵P(k)的积,然后再用步长为k的规范化自相关系数ωk进行加权,即得到基于步长为k的转移矩阵预测结果Tk,即
Tk=ut·P(k)·ωk,
k=2006-t,t=2005,2004,…,1984 。
(12)
将各步长的预测结果Tk相加得到
(13)
概率向量T中各元素的最大值对应的状态即为预测值,见表5。
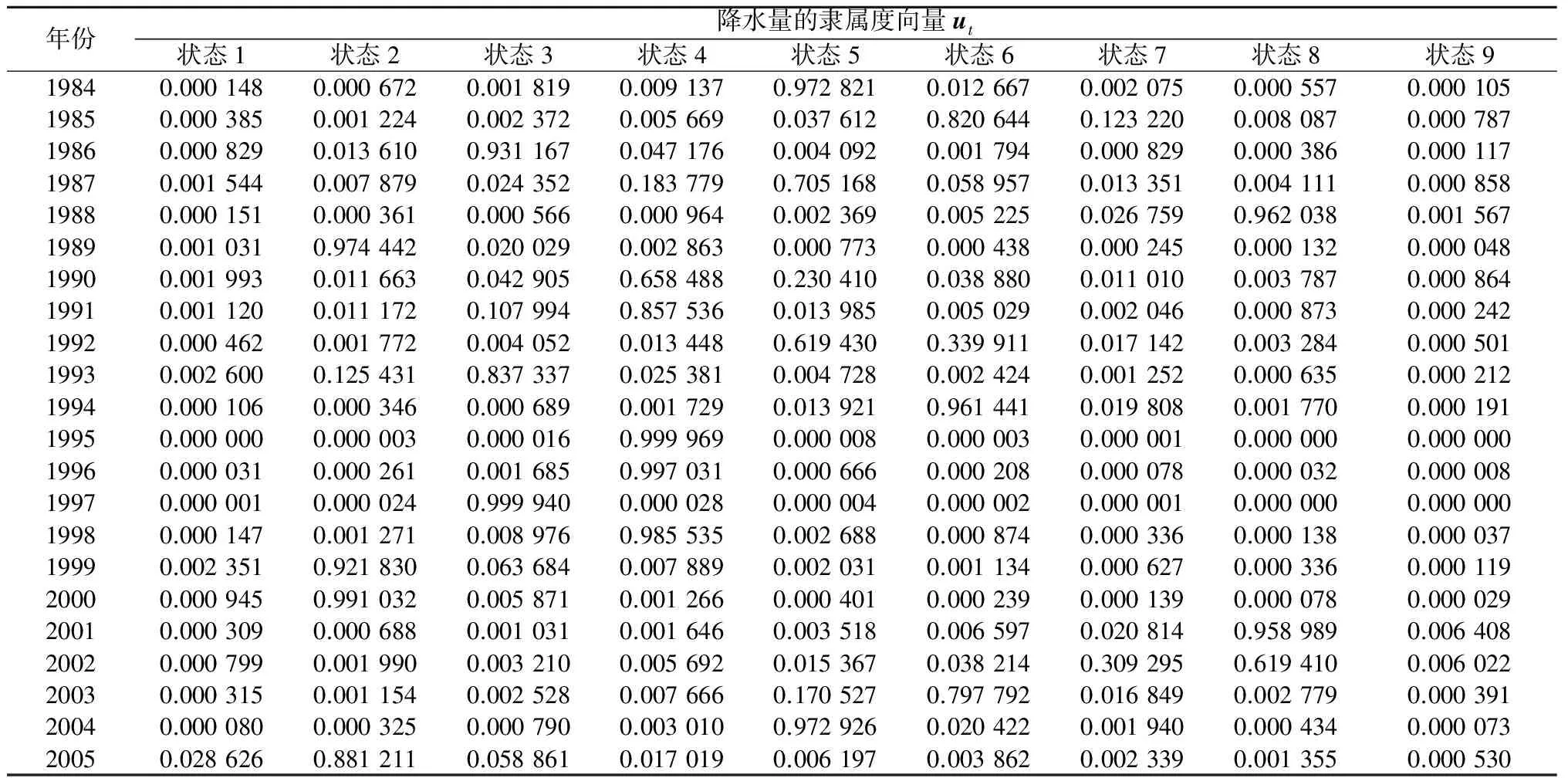
表4 1984—2005年降水量隶属度Table 4 Membership of precipitation from 1984 to 2005
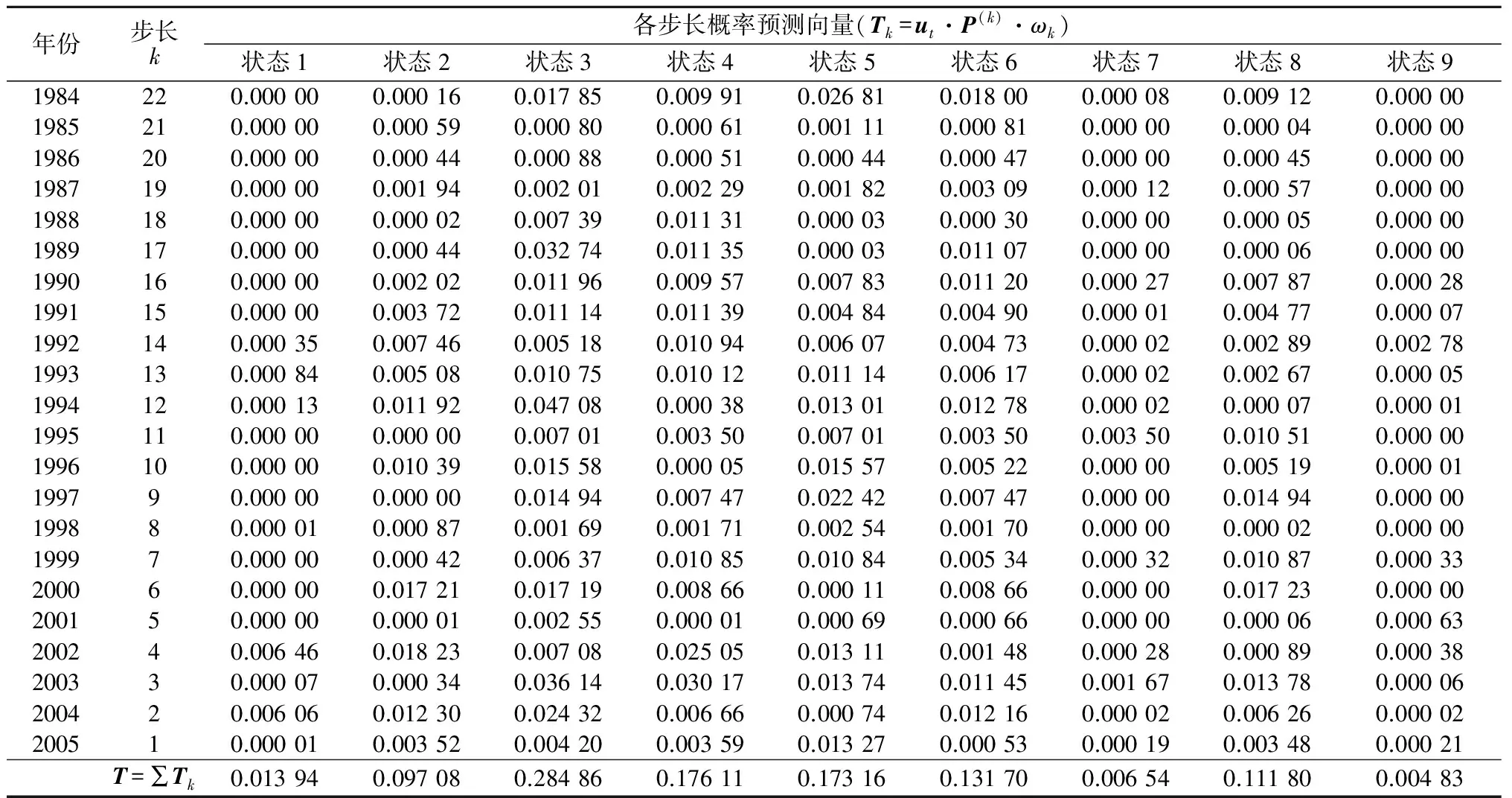
表5 2006年降水状态预测Table 5 Prediction result of precipitation state in 2006
由表5可知,概率向量T中各元素的最大值为0.284 86,对应状态3,即该模型预测2006年的降水状态编号为3,由表2知,榆林市2006年的降水状态编号正是3,预测正确。
(7) 重复上述步骤逐年预测2007—2015年的降水状态,结果如表6。
(8) 在本文状态划分的基础之上,应用传统加权马氏链预测2006—2015年的降水状态,结果如表6。
(9) 状态预测结果分析:
由表6知,2006—2015年共计10 a的状态预测,本文所建模型的预测结果全部与实际一致(准确率达100%),而传统加权马氏链的预测准确率只有70%。
表6榆林市2006—2015年降水状态预测结果
Table6PredictionresultofprecipitationstateinYulincityfrom2006to2015
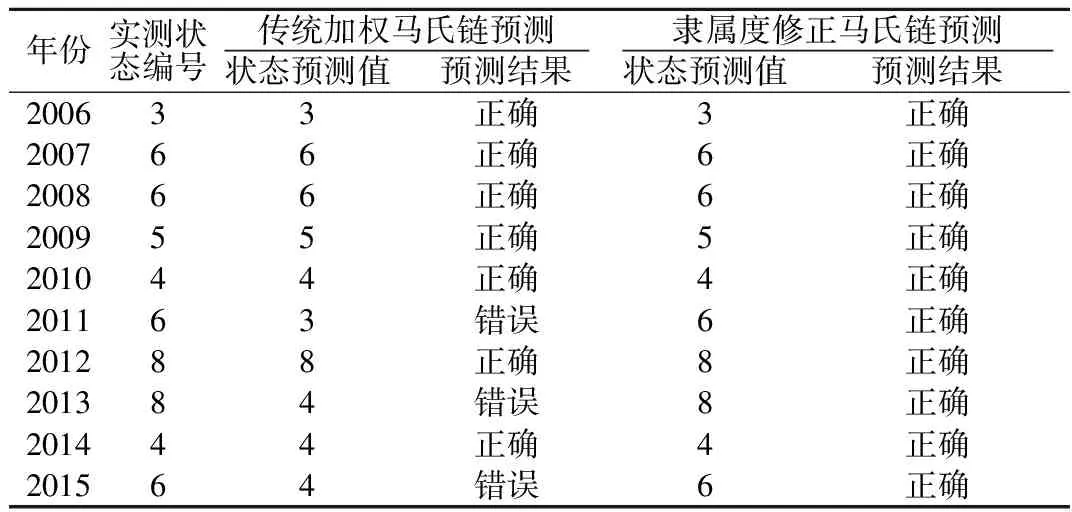
年份实测状态编号传统加权马氏链预测隶属度修正马氏链预测状态预测值预测结果状态预测值预测结果200633正确3正确200766正确6正确200866正确6正确200955正确5正确201044正确4正确201163错误6正确201288正确8正确201384错误8正确201444正确4正确201564错误6正确
传统马氏链对于2013—2015年的预测结果全是4,其中有2个是错误的,而由表2知状态4恰恰是实测序列里出现次数最多的,达到12次,说明传统马氏链的预测结果会受到状态在实测序列里出现频率大小的影响,从而降低其预测精度;隶属度修正的模型克服了这个缺点,使得预测精度较传统模型有明显提高。
同时注意到,2013年的实测降水状态编号为8,2014年突然变为4,跨度达到4个状态,体现了降水量波动性大的特点,这也是对降水量精准预测的难点所在。但在这种情况下,该模型依然预测准确,说明本文所建模型预测机制合理,由于隶属度的修正使其蕴含了更丰富的历史信息以致于能和降水的大幅度波动性拟合较好。
4.4 降水量预测及结果分析
在马氏链预测结果基础之上引入模糊集的级别特征值理论预测具体降水数值。因最大概率作用系数θ的取值没有成熟的理论依据,故经多次试算,本文确定θ=57,根据式(7)分别预测2006—2015年的降水量,结果如表7。
表7榆林市2006—2015年降水量预测结果
Table7PredictionresultofprecipitationinYulincityfrom2006to2015

年份实测值/mm预测状态h值预测值/mm相对误差/%2006313.533.0000290.8-7.232007439.465.7491452.42.962008447.566.0000472.15.512009420.854.9997430.32.252010363.944.0000344.2-5.412011445.465.3298419.4-5.842012566.888.0000547.0-3.492013562.587.9141541.2-3.792014378.344.0000344.2-9.012015451.065.3000417.1-7.52
由表7还可知:2006—2015年共计10 a降水量预测值的相对误差全在10%以内,最大相对误差也只有-9.01%,相对误差在5%以内的占到了40%。以上结果表明所建模型合理可行,精度较高,可用于榆林市年降水量的预测。
4.5 榆林市2016—2021年降水量预测
用所建模型动态预测了榆林市2016—2021年的降水量,结果如表8。

表8 榆林市2016—2021年降水量预测结果Table 8 Prediction result of precipitation inYulin city from 2016 to 2021
由表8可知,2016—2018年连续3 a时间,榆林市降水量都明显小于1951—2015年的平均值404.7 mm;2019年降水量较丰; 2020年降水量显著减少,只有不到300 mm,大致为枯水年水平;2021年降水量大概为平水年水平。
5 结论与展望
(1) 降水状态的划分没有绝对的数值依据,尤其是区间两极的一些降水数据,具有明显的模糊特征,从这个角度讲,将降水状态模糊化是合理的。本文利用FCM算法中的隶属函数赋予每个降水量属于各状态的隶属度,使降水状态模糊化的同时,也使得预测时的初始向量蕴含了更多的信息,也因此具有了较高的预测精度。
(2)利用该模型预测了榆林市2016—2021年的降水量,结果表明: 6 a之中,除2019年降水较丰、2021年为平水年之外,其余4 a降水量都明显少于过去65 a的平均水平,尤其是2020年,年降水还不到300 mm,这可能会对榆林市造成一定程度的干旱影响。
(3) 隶属函数的构造方法有很多,哪一种方法最适于降水序列还需进一步实践、探讨。
(4) 因降水量不能严格满足马尔可夫模型的一阶无后效性,故采用多步长、加权2种方法进行修正。但对于转移矩阵最大步长的选择却一直缺乏严谨的理论依据,普遍经验性地采用状态数作为最大步长,这样做在很多情况下都限制了预测的精度。本文根据榆林市降水数据经过多次试验,确定了最大步长为22,并取得了满意的预测结果。但该步长的选择具有极强的针对性,榆林之外的地区未必适用。因此,如何在理论上确定合理的最大步长是马尔可夫链预测的一个重点问题。
(5) 级别特征值理论中的最大作用系数θ通常都取为2或4,但这同样没有成熟的理论依据。本文经过多次试验发现θ>40时才能取得很好的结果,θ=57时全局结果相对最佳。因此,最大作用系数θ的选择仍需进一步研究。
[1] 黄 华,蔡 仁,穆振侠,等.基于模糊集修正加权马尔可夫模型在新疆降水预测中的应用[J].新疆农业科学,2015,52(10):1891-1898.
[2] 李 俊,毕华兴,李笑吟,等.有序聚类法在土壤水分垂直分层中的应用[J].北京林业大学学报,2007,29(1):98-101.
[3] 武琳琳.基于Fisher最优分割法的聚类分析应用[D].郑州:郑州大学,2013:13-30.
[4] 温海彬.马尔可夫链预测模型及一些应用[D].南京:南京邮电大学,2012:7-31.
[5] 杨皓翔,梁 川,崔宁博.基于加权灰色-马尔可夫链模型的城市需水预测[J].长江科学院院报,2015,32(7):15-21.
[6] 万 臣,李建峰,赵 勇,等.基于新维BP神经网络-马尔科夫链模型的大坝沉降预测[J].长江科学院院报,2015,32(10):23-27.
[7] 何嘉婧,王晋东,于智勇.基于模糊C-均值的改进人工蜂群聚类算法[J].计算机应用研究,2016,33(5):1342-1345.
[8] 李培强,李欣然,陈辉华,等.基于模糊聚类的电力负荷特性的分类与综合[J].中国电机工程学报,2005,25(24):73-78.
[9] 李 中,苑津莎.不同相似度测量方式的模糊C均值聚类分析[J].计算机工程与应用,2011,47(18):17-18.
[10] 孙才志,林学钰.降水预测的模糊权马尔可夫模型及应用[J].系统工程学报,2003,18(4):294-299.
[11] 王 涛,钱 会,李培月.加权马尔可夫链在银川地区降雨量预测中的应用[J].南水北调与水利科技,2010,8(1):78-81.
[12] 王化齐,张茂省,党学亚.榆林地区降水蒸发时间序列的多尺度特征和突变分析[J].水电能源科学,2010,28(9):1-4.
[13] 姚美娟,陈建平,王 翔,等.基于最优分割分级法的月球撞击坑分级及其演化分析[J].岩石学报,2016,32(1):119-126.
Prediction of Annual Precipitation by Weighted Markov ChainBased on Membership Modification
MIAO Zheng-wei1,XU Li-gang2
(1.Department of Hydraulic Engineering,Hebei University of Water Resources and Electric Engineering,Cangzhou 061001, China; 2. Scientific Research Institute of Water Conservancy of Ningxia, Yinchuan 750021, China)
The annual precipitation series of Yulin city from 1951 to 2015 was divided into 9 states by the Fisher optimal partition method. The weighted Markov chain model was established by taking the standardized autocorrelation coefficients as weights. With the mean value of all precipitation in the same state as the cluster center, the membership function of the Fuzzy C-Means was applied to calculate the membership of annual precipitation, and the membership vector was taken as the initial state vector for the time period. The precipitation state from 2006 to 2015 in Yulin city was predicted year by year. All the results agree with the reality. Based on the prediction results of Markov Chain, the precipitation was predicted respectively from 2006 to 2015 by the level characteristics value of Fuzzy Sets, and the relative error of all the prediction results is less than 10%. The preliminary results show that the model of weighted Markov chain based on membership modification is feasible.
precipitation prediction;membership;weighted Markov chain;fuzzy sets;Yulin
2016-09-01;
2016-09-29
苗正伟(1981-),男,山东聊城人,讲师,硕士,主要从事水文水资源方面的研究。E-mail:myjxbe@126.com
10.11988/ckyyb.20160893
P333
A
1001-5485(2018)01-0040-07
(编辑:王 慰)

