注塑成型有限元分析管理和成型工艺优化系统
凌成智,胡广洪
(上海交通大学 塑性成形技术与装备研究院,上海 200030)
注塑成型有限元分析管理和成型工艺优化系统
凌成智,胡广洪
(上海交通大学 塑性成形技术与装备研究院,上海 200030)
目的 针对注塑成型工艺过程,开发有限元分析项目流程管理和工艺参数优化的集成系统。方法 参考企业项目流程,开发项目流程管理模块,使用多元回归拟合配合改进的模拟退火算法进行工艺参数的优化,通过塑料托盘翘曲变形量的优化来验证优化方法的准确性,进行塑料托盘的CAE分析正交试验,使用多元回归拟合试验数据并进行拟合优度检验,分别使用Isight和改进的模拟退火算法进行最优解的求解并对比计算结果,最后对得到的最优参数组合进行CAE分析得到变形量,将变形量与正交试验变形量对比。结果 在回归方法中,使用惩罚系数为2的多项式岭回归效果较好,其优度指标R2为0.975,改进的模拟退火算法计算结果与Isight软件自适应模拟退火算法的计算结果基本一致,最优参数组合在Moldflow分析中的变形量为0.6805 mm,与之前的最小变形量0.7436 mm相比更小。结论 使用回归拟合配合改进的模拟退火算法开发的工艺参数优化程序能起到较好的工艺参数优化效果。
注塑成型;有限元分析;项目管理;工艺优化
目前在注塑工艺设计过程中,使用CAE软件进行仿真分析已经成为其中至关重要的一环,采用有限元计算方法,模拟整个注塑过程,并分析成型工艺对注塑成型产品质量的影响,以帮助设计人员及早发现并解决问题[1],因而,CAE软件在提高研发效率,降低研发成本等方面发挥了重要作用。在处理大量的重复性的CAE计算以及成型工艺参数的优化问题上,使用单一 CAE软件就显得效率低下了,因此,CAE集成系统应运而生,成为目前 CAE技术发展的一个重要方向。国内外的许多软件公司、高校和研究机构着力于研发围绕CAE软件的集成系统或平台[2—3]。
文中描述的是针对注塑成型进行有限元分析,开发了 CAE项目流程管理和成型工艺参数优化的集成系统,实现对注塑成型有限元分析项目流程进行科学、系统的管理,将人力从具有繁重的重复性的有限元分析任务中解放出来,同时,为注塑成型工艺参数的优化提供了高效、精确的研发工具。
1 软件架构设计
本系统整体上使用客户端/服务器(Client/Server)结构。客户端为本软件主体,服务器则为存放各类数据的数据库。本系统主要有用户管理、项目流程管理、集成研发工具3个功能模块。3个模块以及相应的数据库都相互独立,方便根据需求进行扩展和对数据的管理、维护。
本系统主要使用C#语言,在.NET平台上进行开发。前2个模块通过在.NET上对关系型数据库进行操作的方式,实现相应的功能。集成研发工具模块中,使用读取数据库正交表的方式实现工艺参数的设置;使用VB脚本调用Moldflow SynergyAPI来驱动CAE软件,然后在程序里重开进程,运行VB脚本完成自动运行 Moldflow软件的功能;调用数据计算的Python脚本完成工艺参数优化功能。
2 用户和项目流程管理
有限元分析是现代企业成型工艺研发的一个必不可少的步骤,在整个研发过程中与其他环节有紧密的联系,同时,人员上也存在不同工程师之间的协调,因此,在项目的开展过程中,对人员和任务进行清晰、科学的管理很有必要。在用户管理模块中,对所有的用户都进行了权限管理,每个工程师分工明确,在登陆系统之后只能调用与权限对应的功能模块。本系统将人员分为4个类别:超级管理员、总工程师、高级工程师、工程师。超级管理员主要负责对用户信息进行管理,如用户注册审批、用户信息修改、用户账号销毁等,注册管理界面见图1;总工程主要负责项目的新建和撤销,在新建项目后需要将项目细分为具体的任务;高级工程师的工作是将项目的具体任务分配给具体工程师,审核工程师提交的任务,项目完成时进行提交等,任务分配界面见图2;工程师执行通过“我的任务”菜单栏查看自己任务,执行并提交任务。
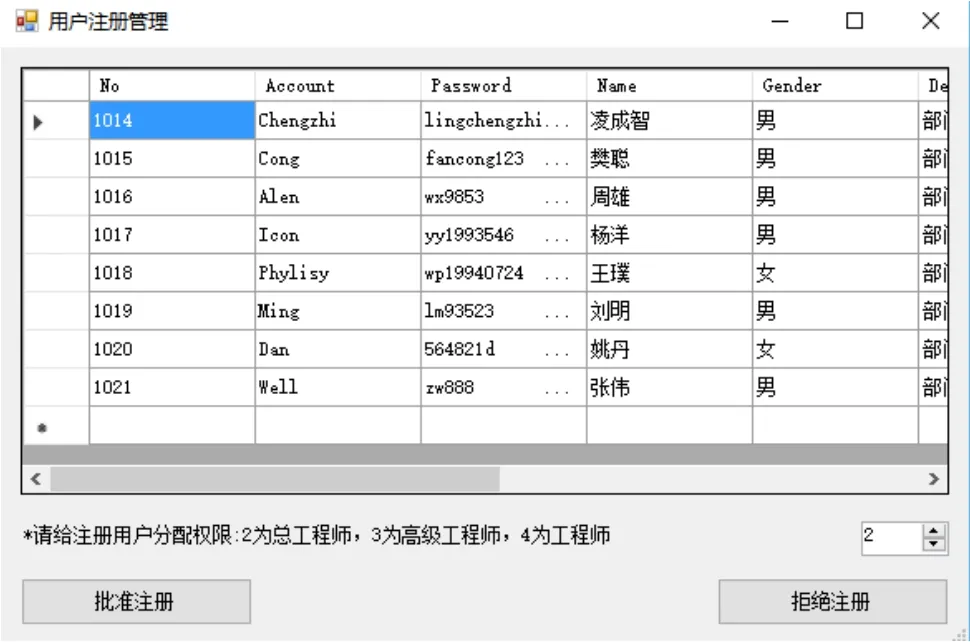
图1 用户注册管理界面Fig.1 Interface of user registration management
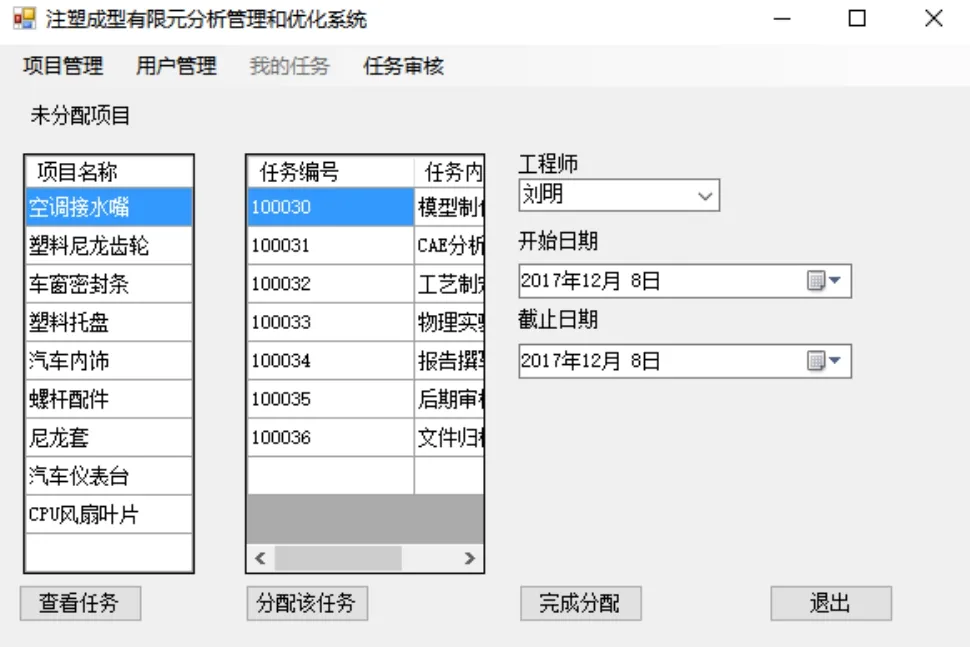
图2 任务分配界面Fig.2 Interface of task assignment
3 注塑成型工艺集成研发工具
3.1 基于Moldflow API的CAE分析任务自动运行程序设计
在本系统中,首先通过正交试验的方法设置成型工艺参数,然后调用Synergy API对Moldflow分析软件进行驱动,实现复制模型,设置参数,同步运行以及结果数据的自动读取,从而极大提高了CAE分析的工作效率和后期数据处理的准确性。整个流程见图3。

图3 CAE分析任务自动与运行程序流程Fig.3 Work flow of automatic operation analysis of CAE
所有的实验及数据都是以塑料托盘为例,分析内容包括冷却、填充、保压、翘曲,材料为PP(POLYFLAM RPP 374 ND CS1),具体模型见图4。
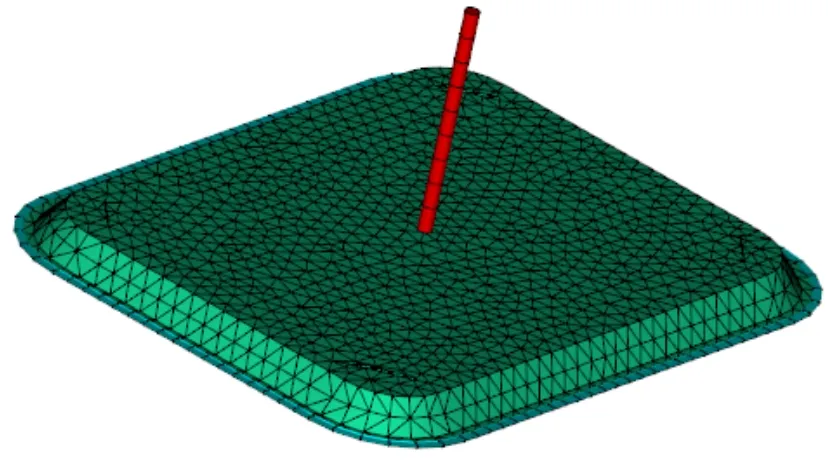
图4 塑料托盘模型Fig.4 Model of plastic tray
驱动MOLDFLOW软件进行批量CAE运算的流程为:首先将系统计算生成的实验数据格式化为参数字符串;然后在系统中重开进程运行VB脚本,将前一步生成的字符串传入脚本作为参数;最后调用Synergy API提供的相应接口依次循环执行打开模型、设置参数、提交分析和复制模型等操作。VB脚本中程序运行逻辑具体情况见图5。
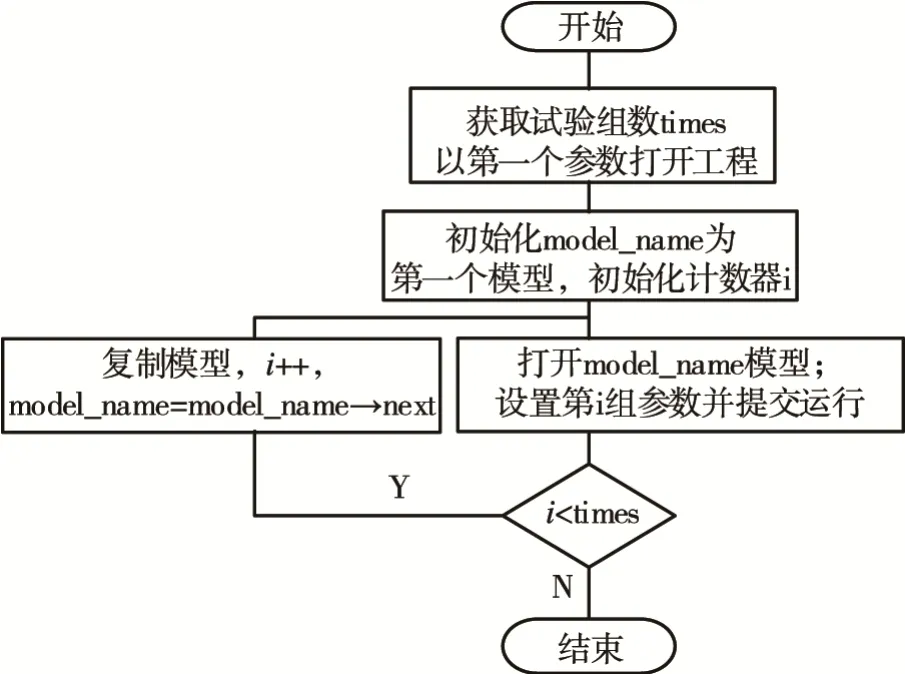
图5 批量运行CAE分析程序Fig.5 Block diagram for batch run of CAE analysis
CAE软件分析结果数据的获取,同样也是通过VB脚本调用Synergy API进行实现的。本系统可以获取各目标参数的最大、最小及平均值。图6显示了部分分析数据的自动获取情况。
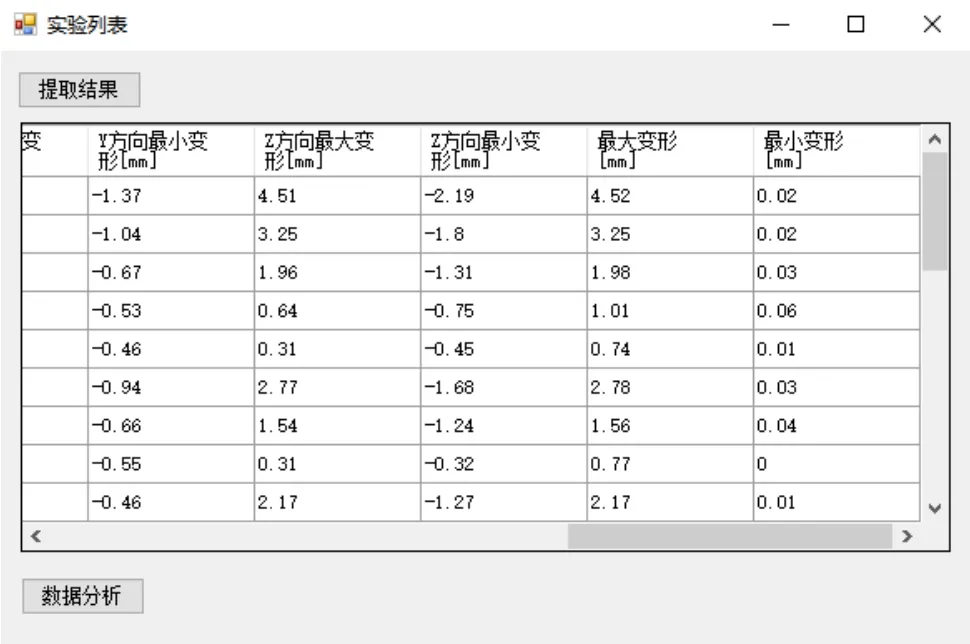
图6 分析结果获取界面Fig.6 Interface of retrieving analysis results
3.2 基于回归分析和改良模拟退火算法(SA)的工艺优化程序
成型工艺参数优化程序是整个系统的核心。本系统的工艺优化流程是:按照正交试验设计程序,设计关于工艺参数的正交试验,通过自动化驱动程序驱动CAE软件(Moldflow)进行计算,提取得到结果数据,将正交试验参数组和结果数据的某一特定分析项一起作为样本数据,对这些样本数据进行多元回归拟合,最后对拟合的结果使用最优解搜寻算法进行最值求解。得到的结果即为最优的工艺参数组合。
回归过程使用的回归方法为带有二次项的多项式回归模型。其本质上是对多元线性回归的一个扩展。首先介绍一下简单的多元线性回归,其回归方程的一般形式为:
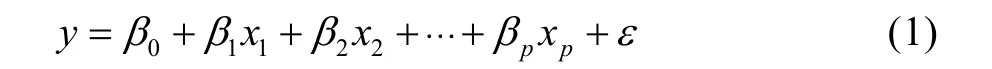
式中:β1,β2…βp为p个待求的回归系数;β0为常数项系数;ε为随机误差;y为因变量,即目标函数;xi为第i个自变量。文中使用回归方法为scikit-learn工具中的岭回归[4],这种回归方法是在普通的“最小二乘法”的残差平方和项中加入一个惩罚项(α|β|2)来解决共线性和病态数据的问题[4—6]。其中α为惩罚系数,α值的确定是由以α为自变量,拟合效果指标Score为因变量的函数的最大值处确定,见图7。
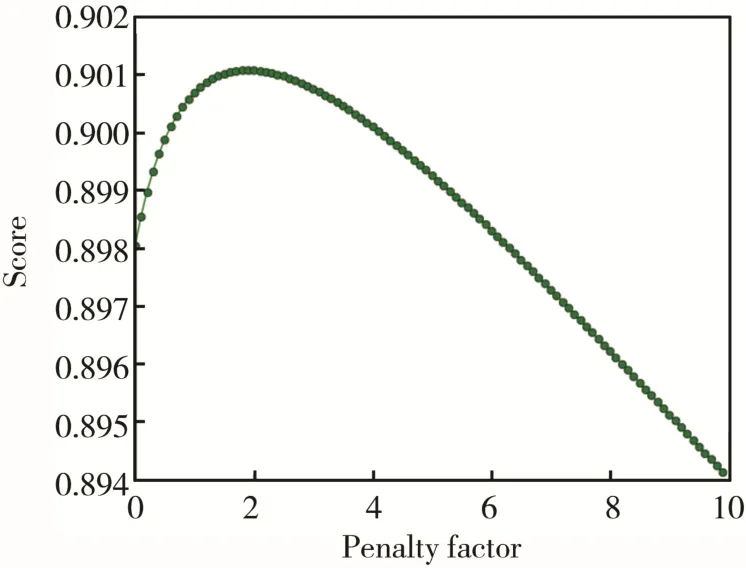
图7 惩罚系数与拟合效果之间的关系Fig.7 Relationship between penalty factor and fitting effect
由此,本系统使用扩展参数组的方式来将其扩展为多项式回归[7—9]。当只有想x1,x2两个参数时,简单线性拟合时所求的系数有常数项、x1的系数、x2的系数,而多项式回归时则需计算x12,x22,x1x2值,并将其加入参数,所求系数增加x12的系数、x22的系数、x1x2的系数。这样就可以求出带有二次项的回归结果,见式(2)。
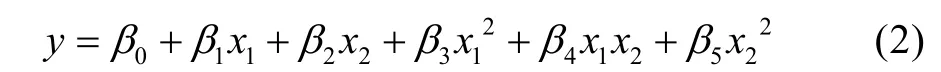
文中使用改进的模拟退火算法求解最优参数组合,其算法流程见图8。改进之处包括。
1) 初始值的选取:与一般的随机取初始值不同,文中使用的初始值为田口方法的极差分析得到的局部最优组合。该初始值在正交试验的水平间隔上已经是最优解,在该初始值基础上开始搜寻,以提高效率。
2) 新解的产生方式:通常新解产生方式是将固定步长加在原始解的一个随机参数上形成新解。文中算法则采用与温度相关的步长,在降温过程中步长也随之变小,以增加算法的局部搜索能力和降低丢失最优解的概率[10]。
3) 新的降温规则:配合新的初始值选取方式(见式(3)),文中采用较低的初始温度以及缓慢的降温方式。(θ为降温系数,文中的算法中取0.9)。

4) 记录历史最优解,在不增加时间、空间复杂度的情况下保证算法结果优于或等于算法结束时的当前解。
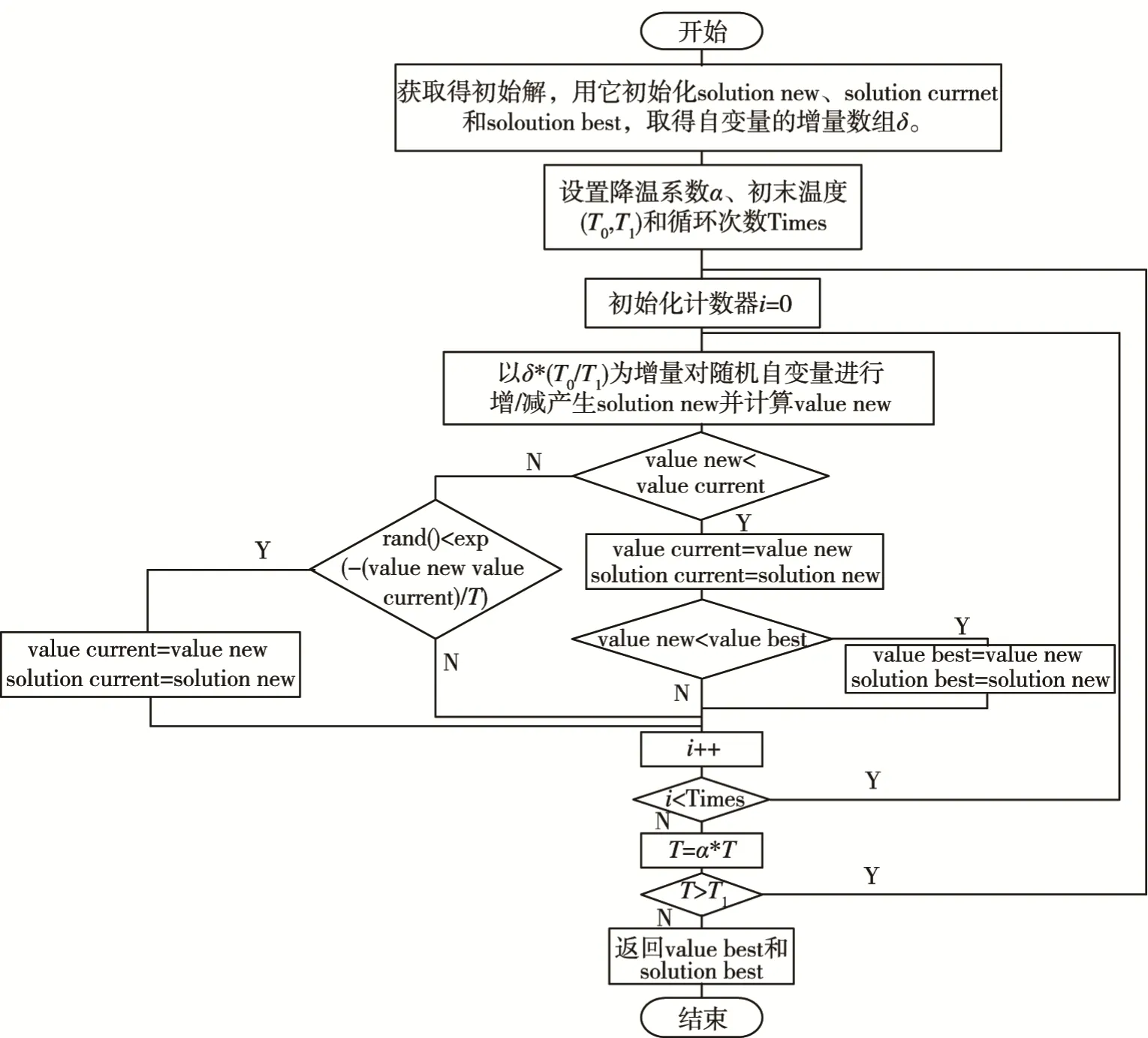
图8 改进的模拟退火算法Fig.8 Improved simulated annealing algorithm
4 塑件变形量的优化分析
本节以制件翘曲变形量为目标函数,利用本系统进行优化分析,从而降低制件的最终变形量[11]。首先在本系统下进行2组五因素五水平的正交试验[12],两组试验一共50次CAE分析,将第一组的数据用于拟合各工艺参数与变形量最大值之间的关系,第二组数据用于验证该拟合结果的效果。最后对本系统得出的最优参数组合进行CAE分析实验验证,其中设置的参数及其水平区间见表1。
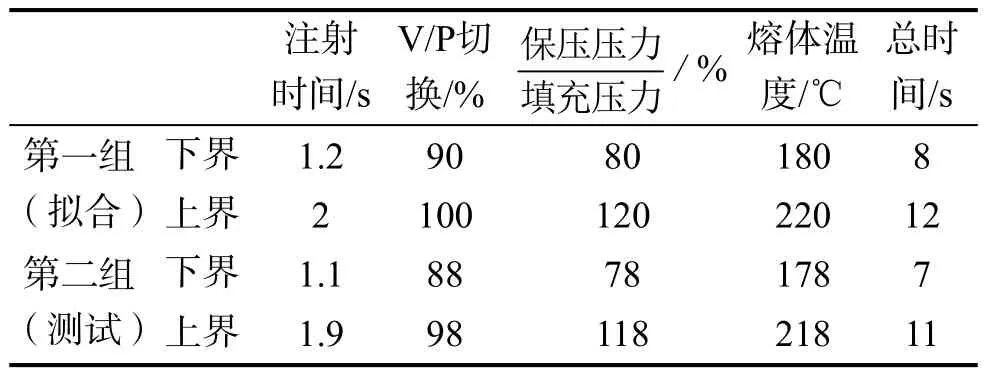
表1 注塑成型CAE分析参数表Tab.1 CAE analysis parameters of injection molding
通过本系统进行正交试验的设计,得到的参数表界面见图 9。调用 Moldflow计算后提取的结果界面见图6,Moldflow分析结果第一组的最大变形量分别为4.52, 3.25, 1.98, 1.01, 0.74, 2.78, 1.56, 0.77, 2.17,3.77, 1, 2.96, 1.69, 3.26, 1.12, 2.5, 0.9, 1.85, 1.18, 3.08,0.95, 1.55, 4.01, 1.71, 0.95 mm;第二组变形量分别为4.78, 3.56, 2.32, 1.15, 0.77, 3.04, 1.9, 0.81, 2.67, 4.1,1.06, 3.37, 2.08, 3.69, 1.22, 2.87, 0.98, 2.07, 1.31, 3.49,1.03, 1.69, 4.33, 2.25, 1.09 mm。

图9 正交试验参数Fig.9 Orthogonal experimental parameters
根据分析结果,本系统对第一组实验数据分别使用普通最小二乘法线性回归、普通最小二乘法多项式回归和惩罚系数为2的多项式岭回归拟合,将第二组的正交试验参数代入第一组数据的各个拟合结果进行计算预测值(predict value),得到的结果与第二组数据在 Moldflow中的分析得到的值(true value)进行对比,见图10—12,其中横坐标为试验组数。
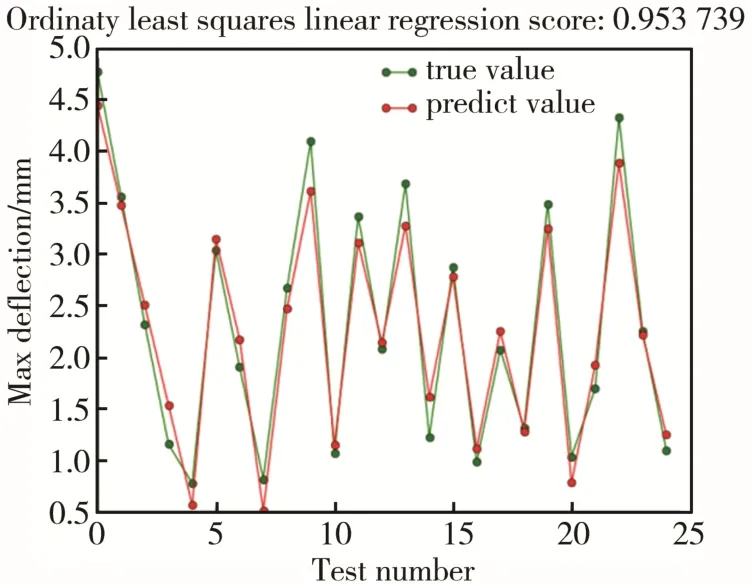
图10 普通最小二乘法线性回归Fig.10 Ordinary least squares linear regression
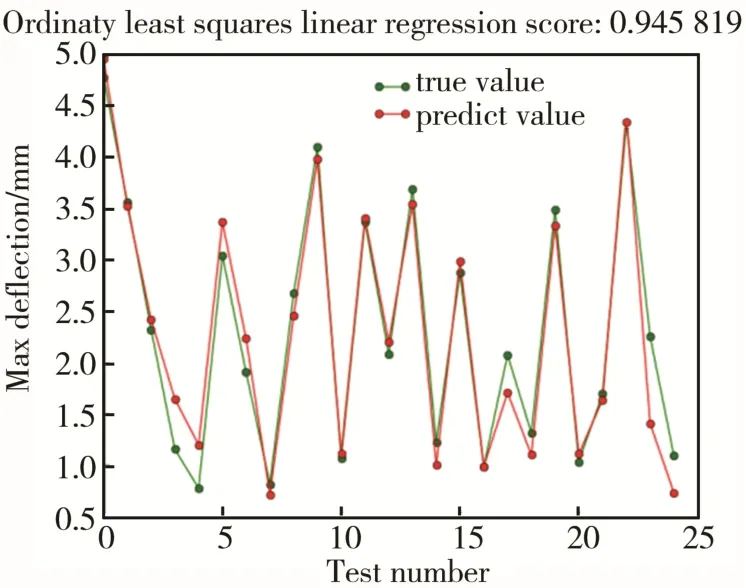
图11 普通最小二乘法多项式回归Fig.11 Ordinary least squares polynomial linear regression

图12 α值为2时的多项式岭回归Fig.12 Polynomial ridge regression when α=2
从图10—12可知,使用惩罚系数为2的多项式岭回归效果最好,拟合效果指标达到 0.975。说明这个回归模型是可靠的。且回归结果模型见式(4)。
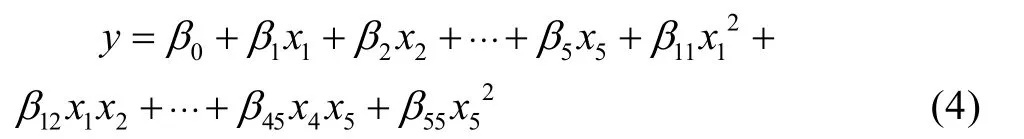
式中:x1,x2,x3,x4,x5分别为注射时间、V/P切换、保压压力、熔体温度、“注射+保压+冷却”时间。式(4)各项系数见表2。
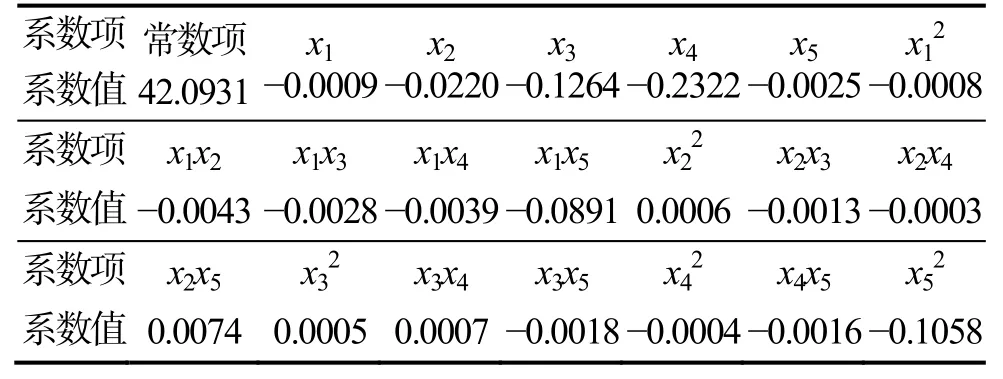
表2 回归多项式系数表Tab.2 Coefficients of polynomial regression
在回归模型基础上,使用改进的模拟退火算法进行最优参数组合的搜寻,搜寻过程当前值随着每次降温的变化曲线见图13,得到的最优解组合见表3。
为验证本算法的准确性,在Isight软件上也使用这一回归模型(4)进行了计算[13],具体系数见表 2,参数的取值范围为表 1中的第一组中实验参数的范围,求出的最优组合见表3。
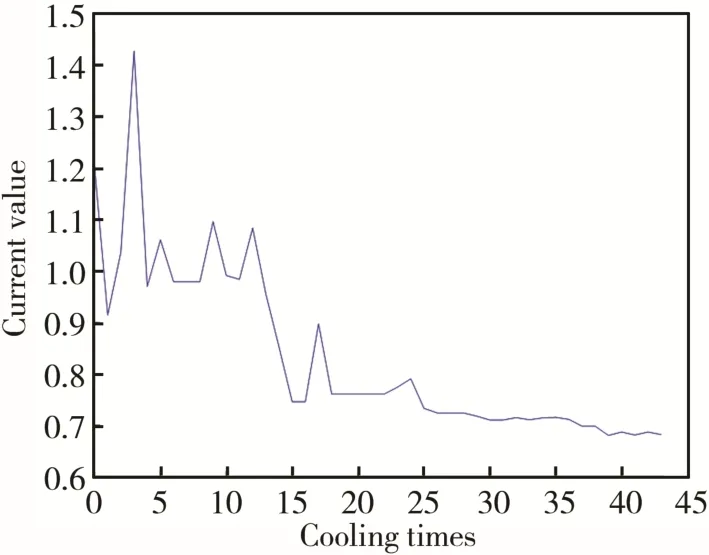
图13 改进的SA算法当前解变化曲线Fig.13 Current solution curve of improved SA algorithm
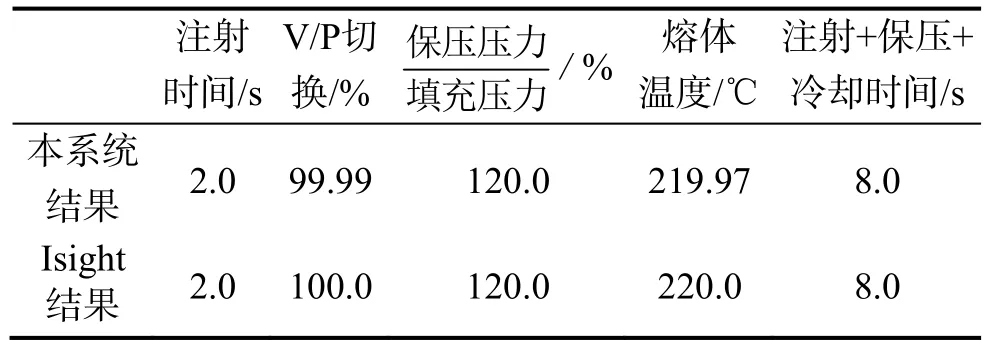
表3 模拟退火算法求出的最优参数组合Tab.3 Optimal combination for parameters of simulated annealing algorithm
由表4可知,两种模拟退火算法得出最优解的参数组合几乎一致,除V/P切换和熔体温度有0.01%的误差外,其余几个参数都一致,说明了本系统改进的模拟退火算法准确有效。
将得到的最优参数组合导入 Moldflow进行分析,结果见图14,得到的最大变形量为0.6805 mm,比正交试验25组CAE分析的最优结果0.7436更小,优化力度为 9.3%,进一步说明本算法准确有效,且说明回归与最优解搜寻整个程序精确有效。
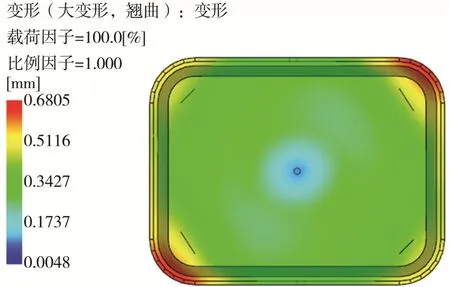
图14 最优参数组合的分析结果Fig.14 Analysis result of the best parameter combination
5 结论
本系统开发了3个功能模块:用户管理、项目流程管理和集成研发工具,其能有效地实现对企业用户、项目流程的管理以及注塑成型工艺参数的优化。用户管理和项目流程管理有利于企业明确分工、加强协作、降低研发成本、提高工作效率。集成研发工具模块一方面为大量重复的CAE分析工作提供了一个简单、高效的解决方案,另一方面基于多元回归和改进的模拟退火算法实现了对成型工艺参数的优化。通过与专业优化软件的结果对比,验证了本系统计算结果的精确性和有效性。
[1] 王小明, 赵明娟, 陈炳辉, 等. Moldflow 在注塑成型翘曲优化中的应用[J]. 塑料工业, 2011, 39(4): 49—51.WANG Xiao-ming, ZHAO Ming-juan, CHEN Bing-hui,et al. Application of Moldflow in Warp Optimization of the Injection Molding[J]. China Plastics Industry, 2011,39(4): 49—51.
[2] MATIN I, HADZISTEVIC M, HODOLIC J, et al. A CAD/CAE-integrated Injection Mold Design System for Plastic Products[J]. The International Journal of Advanced Manufacturing Technology, 2012, 63(5): 595—607.
[3] 陈华书, 胡广洪. 金属体积成形有限元分析管理与工艺优化平台[J]. 热加工工艺, 2013, 42(23): 125—128.CHEN Hua-shu, HU Guang-hong. Finite Element Analysis Management and Process Optimization Platform for Metal Volume Forming[J]. Hot Working Technology,2013, 42(23): 125—128.
[4] PEDREGOSA F, VAROQUAUX G, GRAMFORT A, et al. Scikit-learn: Machine Learning in Python[J]. Journal of Machine Learning Research, 2011, 12(10): 2825—2830.
[5] LIU X Q, GAO F, XU J W. Linearized Restricted Ridge Regression Estimator in Linear Regression[J]. Communications in Statistics-Theory and Methods, 2012, 41(24):4503—4514.
[6] 任维雅, 李国辉. 面向监督学习的稀疏平滑岭回归方法[J]. 国防科技大学学报, 2015, 37(6): 121—128.REN Wei-ya, LI Guo-hui. Sparse Smooth Ridge Regerssion Method for Supervised Learning[J]. Journal of National University of Defense Technology, 2015, 37(6):121—128.
[7] KONG D, BONDELL H D, WU Y. Domain Selection for the Varying Coefficient Model Via Local Polynomial Regression[J]. Computational Statistics & Data Analysis,2015, 83: 236—250.
[8] 卢静波, 吴艺能. 非线性回归模型的线性变换和正交多项式回归[J]. 统计与决策, 2009, 2009(23): 13—14.LU Jing-bo, WU Yi-neng. Linear Transformation and Orthogonal Polynomial Regression in Nonlinear Regression Model[J]. Statistics and Decision, 2009, 2009(23):13—14.
[9] 黎明, 陈颖, 杨楠. 应用回归分析[M]. 上海: 复旦大学出版社, 2008.LI Ming, CHEN Ying, YANG Nan. Application of Regression Analysis[M]. Shanghai: Fudan University Press,2008.
[10] 袁澎, 艾芊, 赵媛媛. 基于改进的遗传-模拟退火算法和误差度分析原理的PMU多目标优化配置[J]. 中国电机工程学报, 2014, 34(13): 2178—2187.YUAN Peng, AI Qian, ZHAO Yuan-yuan. Research on Multi-objective Optimal PMU Placement Based on Error Analysis Theory and Improved GASA[J]. Proceedings of the CSEE, 2014, 34(13): 2178—2187.
[11] 孙宝寿, 陈哲, 吴真繁, 等. 薄壁注塑件翘曲影响因素分析及优化研究进展[J]. 机械制造, 2009, 47(12): 25—29.SUN Bao-shou, CHEN Zhe, WU Zhen-fan, et al. Analysis and Optimization of Warping Factors of Thin Wall Injection Molding Parts[J]. Machinery, 2009, 47(12): 25—29.
[12] 郎志正. 质量管理及其技术和方法[M]. 北京: 中国标准出版社, 2003.LANG Zhi-zheng. Quality Management and Its Technical Methods[M]. Beijing: Standards Press of China, 2003.
[13] VAN D V A, KOCH P. Isight Design Optimization Methodologies[J]. ASM Handbook, 2010, 22: 79.
Finite Element Analysis Management and Process Optimization System of Injection Molding
LING Cheng-zhi,HU Guang-hong
(Institute of Plastic Forming Technology and Equipment, Shanghai Jiao Tong University, Shanghai 200030, China)
The paper aims to develop an integrated system of project work flow management and process parameter optimization for injection molding finite element analysis. The project process management module was developed in line with the company's project process. Multiple regression methods were used in combination with the improved simulated annealing algorithm to optimize process parameters. Cases of plastic tray warpage deformation optimization were used to verify the accuracy of the optimization method and carry out CAE analysis and orthogonal test for plastic tray. The multivariate regression method was used to fit the test data and calculate the score. The optimal solution was solved with Isight's ASA and the improved simulated annealing algorithm respectively. And their results were compared. CAE analysis was performed with parameters of the optimal solution; the max warpage of analysis result was obtained, and the warpage was compared with those of orthogonal test.Polynomial ridge regression with penalty coefficient of 2 has the best regression effect and itsR2was 0.975. The calculation result of the improved simulated annealing algorithm was consistent with that of Isight's ASA. The warpage of the optimal parameters in the Moldflow analysis was 0.6805 mm, which was smaller than the previous minimum warpage in orthogonal test of 0.7436 mm. The process parameter optimization program based on regression fitting and the improved simulated annealing algorithm can optimize parameters to some extent.
injection molding; finite element analysis; project management; process optimization
2017-12-10
凌成智(1994—),男,硕士研究生,主要研究方向为计算机辅助工程技术。
胡广洪(1973—),男,博士,副研究员,主要研究方向为高分子材料成型工艺、高分子材料合金化技术、材料成型CAD/CAE/CAM。
10.3969/j.issn.1674-6457.2018.01.021
TQ320
A
1674-6457(2018)01-0161-06

