10kW冲压空气涡轮叶片的气动设计与数值模拟∗
肖云峰 周秀博 张志莲 吕 涛 付国华
(1.北京石油化工学院机电工程学院;2.北京化工大学机电工程学院机械工程学院;3.中国中轻国际工程有限公司)
10kW冲压空气涡轮叶片的气动设计与数值模拟∗
肖云峰1周秀博2张志莲1吕 涛1付国华3
(1.北京石油化工学院机电工程学院;2.北京化工大学机电工程学院机械工程学院;3.中国中轻国际工程有限公司)
基于Wilson理论方法,采用MATLAB编程仿真软件作为优化工具,对冲压空气叶片进行设计,计算出冲压空气涡轮叶片24个截面处的弦长和安装角,通过多项式拟合进行修正,利用SolidWorks三维实体建模。运用NUMECA对模型进行数值模拟,分析不同安装角和风速下其输出功率,得到5种安装角下风速-输出功率的曲线图,并分析了设计工况下的叶片静压分布,以及不同叶高处的速度矢量图。
冲压空气涡轮;Wilson理论;叶片优化设计;NUMECA软件;数值模拟
0 引言
民航飞机的发展是全世界关注的重点,安全性是飞机飞行最基础的要求,因此民航规定“飞机必须设计成在所有发动机都失效的情况下仍可操纵”[1],冲压空气涡轮(Ram Air Turbine,简称RAT)作为应急动力装置,可以确保飞机顺利返航着陆。RAT核心部件——叶片,可将来流空气的动能转换为机械能,因此探讨叶片设计成为冲压空气涡轮研究的重要内容,但商用RAT的研制和生产已经被国外公司垄断,鲜有RAT叶片设计方面的论文,所以,深入研究RAT叶片设计方法具有重要意义[2-8]。
为了探究RAT的设计方法,综合对比螺旋桨和水平轴风力涡轮,选择风力机的相关设计理论。风力机的设计已经十分成熟[9],图解法、Glauert设计法、Wilson设计法等等,笔者采用Wilson设计理论,采用MATLAB编程仿真软件作为优化工具,计算出冲压空气涡轮叶片的弦长和安装角,三维实体建模得到模型。并运用NUMECA对模型进行数值模拟,计算不同风速、不同安装角下RAT的输出功率,同时,分析其流场特征[10]。
1 理论基础
1.1 叶素动量理论
动量叶素理论[8],综合了动量理论和叶素理论,计算出风轮旋转面中的轴向诱导因子a和周向诱导因子b。
由动量理论得到作用在微段上的推力和转矩为:

由叶素理论得到作用在微段上的推力和转矩为:

上述两种方式得到的结果是相等的,并由速度三角形可得:

根据以上关系式,通过迭代方法求解轴向诱导因子a和周向诱导因子b。
1.2 Wilson设计理论
Wilson设计法是在Glauert设计法的基础上,研究了叶尖损失和升阻比对叶片最佳性能的影响。Wilson设计理论是以每个叶素截面的风能利用系数最大为目标,约束条件为轴向诱导因子a和周向诱导因子b,得能量方程为:


叶尖损失系数:

运用MATLAB编程,式(7)为目标函数,式(8)为约束条件,迭代求解得到轴向诱导因子a和周向诱导因子b,最后依据式(11)、式(12)分别求得弦长c和安装角ϕ。

2 模型的建立
2.1 叶片参数的选择
功率为10kW;设计风速为100m/s;风轮转速为7 000rpm;叶片数目为2个;功率系数为0.1;叶片半径为300mm;轮毂半径为70mm;叶尖速比为2.2;雷诺数为5×106;翼型[6,11]为ARA-D6%、ARA-D10%、ARA-D13%。
2.2 优化设计
从叶根到叶顶取24个截面,运用MATLAB计算的结果如表1所示。

表1MATLAB计算结果Tab.1 The calculation results of MATLAB
Wilson设计法得到叶片各截面的弦长和安装角皆为最优,但是设计结果显然不符合实际,尤其是叶根部分安装角过大,增加了制造难度及成本,且叶片做功的关键部位为中部和尖部,因此对其进行修正,安装角和弦长修正结果分别如图1、图2所示。
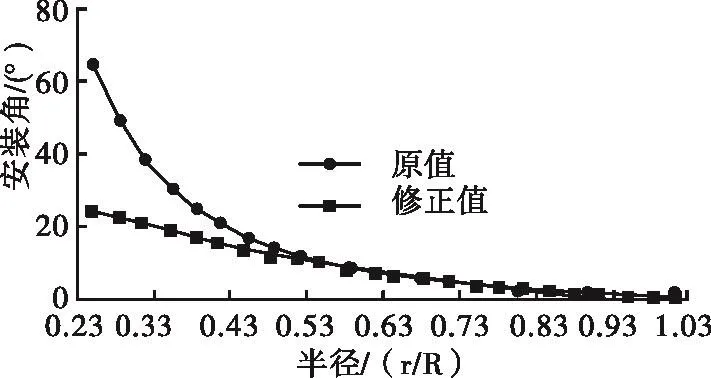
图1 安装角修正图Fig.1 The modified angle installation

图2 弦长修正图Fig.2 The modified chord length
2.3 实体建模
通过Profili软件得到ARA-D系列翼型的数据,结合各截面的弦长和安装角,基于点的坐标几何理论,得到三维空间坐标,运用SolidWorks进行实体建模,如图3所示。

图3 RAT三维示意图Fig.3 The 3D RAT blade profile
3 数值模拟
3.1 计算模型
主要研究冲压空气涡轮在不同安装角以及风速下的性能,选择了5种安装角,分别为25°(设计点),30°(转角 Δϕ=5°),35°(转角 Δϕ=10°),40°(转角Δϕ=15°),5°(转角 Δϕ=20°)。每个安装角下,依据风速的变化(60m/s、80m/s,100m/s,120m/s,140m/s,160m/s,180m/s)分为7种工况,完成35个工况点的计算。
3.2 计算域的选取和网格的划分
冲压空气涡轮的计算域包括内流域和外流域,外流域过大则网格数目过多,导致计算速度减慢,外流域过小则影响计算结果的精确程度。根据冲压空气涡轮的实际情况,进出口位置均选择10倍叶高处,叶片展向位置选择3倍叶高处,选择Bulb结构,进出口皆选择Rounded Topology,如图4所示。

图4 计算域示意图Fig.4 Sketch of computational domain
基于NUMECA[12]的IGG模块进行网格划分,采用向导模式与专家模式相结合的方法,即在向导模式下选择风力机模块,在专家模式下调整网格,得到的网格如图5所示。网格数量为280万,网格质量良好(最小正交性28.8,最大延展比2.5,最大长宽比2346.8),如图6所示。

图5 网格示意图Fig.5 Grid diagram

图6 网格质量图Fig.6 Diagram of grid quality
3.3 计算方法和边界条件
基于NUMECA的FINE/Turbo模块进行数值计算,求解三维定常雷诺平均的N-S方程。时间离散采用4阶Runge-Kutta法迭代求解,并采用多重网格法和局部时间步法加速收敛,选择中心差分离散格式,湍流模型选择k-ε(Extended Wall Function)。
介质设定为理想气体。进口边界条件给定速度、静温、湍流黏性;出口边界条件给定静压;远场边界条件给定速度、静温、静压、湍流黏性;初场设定均匀场,给定压力、温度和速度。迭代步数为10 000步,CFL数为3,全局收敛残差为106,进出口流量差小于0.15%[13]。
3.2 计算结果分析
计算出冲压空气涡轮35种工况下的功率,并绘制速度-输出功率曲线。图7为转速恒定、安装角恒定(设计点)条件下,RAT速度-输出功率曲线图,输出功率随着速度的增加而增加,在风速超过100m/s时,RAT的输出功率即可满足10kW的要求。

图7 设计工况下的风速-功率曲线Fig.7 Wind speed-power curve under design condition
飞机在迫降时,其速度不断变化,导致冲压空气涡轮的工作条件较为复杂,即安装角随着风速的改变而改变,但其对应关系不能得到一个准确的规律。因此,分析了60~180m/s风速下的输出功率,图8为在转速恒定、安装角分别为30°,35°,40°,45°条件下,RAT速度-输出功率曲线图。

图8 不同安装角的风速-功率曲线Fig.8 Wind speed-power curve under different installation angles
由图8可知,在风速超过100m/s时,各个安装角下均可满足功率需求;在风速为60m/s和80m/s的条件下,安装角30°,35°时输出功率较大,安装角40°,45°时输出功率较小,即满足风速较小时,安装角较小输出功率较大,安装角较大输出功率较小;在风速为100m/s时,各个安装角下输出功率的数值相差很小,几乎在20kW左右;在风速为120m/s,140m/s,160m/s,180m/s条件下,安装角40°,45°时输出功率较大,安装角30°,35°时输出功率较小,即满足风速较大时,安装角较大输出功率较大,安装角较小输出功率较小;综上所述,依据风力机原理设计的冲压空气涡轮,只要在风速大于100m/s时,无论安装角如何改变,几乎都可以满足功率的需求。同时,风速较小情况下,安装角较小,功率较大。风速较大情况下,安装角较大,功率较大。
3.5 数值模拟结果分析
设计工况点下,叶片总压如图9所示。压力面上的静压从前缘到尾缘阶梯性减小,尤其是在前缘附近下降较为显著,静压分布较为顺滑,但叶尖部分由于气流收到自由流的影响,旋转区域与非旋转区域有着强烈的掺混,导致叶尖部分静压较小。吸力面前缘40%至50%叶高处,静压较小,导致吸力面上的前缘部分出现了间隙涡。

图9 设计工况下叶片表面静压Fig.9 Static pressure on blade surface under design condition
图10分别为50%、95%叶高处S1流面相对速度矢量图,在50%叶高处有分离涡出现,也对应了图9(b)的吸力面静压分布图。图中清晰的反映出气流流经叶片后其速度的变化情况,叶片下游出现尾迹,尾迹逐渐与主流掺混融合,直至基本消失。

图10 不同叶高处的速度矢量图Fig.10 The relative velocity distribution of the different blade height
4 结论
1)本文运用风力机的设计方法——Wilson理论,采用MATLAB编程仿真软件作为优化工具,计算得到不同叶高处的弦长和安装角,并进行拟合修正,实体建模得到三维图形,经数值模拟分析,安装角在25°至45°间,风速在大于100m/s时即可满足功率10kW的需求。
2)设计工况下,叶尖处不同于有机匣的涡轮,会出现比较强烈的掺混流动。
3)设计工况下,叶高40%至50%处,出现分离涡,即本论文叶片的弦长和安装角有待进一步的改进。
[1]中国民用航空局.CCAR-25-R4[S].2011.
[2]张剑锋,刘思永.冲压空气涡轮性能的局部改进的升力线算法[J].北京航空航天大学学报,1997,22(4):482-486.
[3]刘思永,方祥军,王屏.可调桨距冲压空气涡轮气动特性实验与数值分析[J].航空动力学报,2003(5):587-592.
[4]方祥军,刘思永,王屏.可调桨距冲压空气涡轮混合型流场数值研究[J].北京航空航天大学学报,2004,30(2):152-155.
[5]Glauert H.The elements of airfoil and airs crew theory[M].Cambridge:Cambridge University Press,1983.
[6]张冬雨,杨斐,翟笑天,等.冲压空气涡轮叶尖扰流片研究[C].第五届民用飞机航电系统国际论坛论文集,2016.
[7]王健,卢岳,良杨斐,等.两型冲压空气涡轮翼型气动特性分析[C].第六届中国航空学会青年科技论坛,2014.
[8]王建平,朱春玲.冲压涡轮发电系统数值分析及试验研究[C].第二届中国航空学会青年科技论坛文集,2006.
[9]李庆宜.小型风力机设计[M].北京:机械工业出版社,1986.
[10]姜新春,曾劲松,黄煌.CFD技术在流体机械中的应用与发展[J].轻工机械,2014,32(3):108-110.
[11]张剑锋.冲压空气涡轮特性研究[D].北京:北京航空航天大学,1996.
[12]郭然,贾力平,樊小莉,等.NUMECA系列教程[M].北京:机械工业出版社,2013.
[13]何志霞,王谦,袁建平.数值热物理过程基本原理及CFD软件应用[M].镇江:江苏大学出版社,2009.
Blade Aerodynamic Design and Numerical Simulation for 10kW Ram Air Turbine
Yun-feng Xiao1Xiu-bo Zhou2Zhi-lian Zhang1Tao Lv1Guo-hua Fu3
(1.College of Mechanical Engineering,Beijing Institute of Petrochemical Technology;2.College of Mechanical Engineering,Beijing University of Chemical Technology;3.China Light Industry International Engineering Co.,Ltd.)
The Ram Air Turbine blade is optimal designed based on the theory of Wilson method.The blade chord length and installation angle in 24 cross-section are calculated by MATLAB simulation software and the calculation results are modified through polynomial fitting.The three-dimension CAD model of the blade is developed using SolidWorks software.The model is numerical simulated by NUMECA to analysis the output power under different installation angle and wind speed,then the wind-power output curve under 5 kinds of installation angle is obtained,and also analyzes the blade static pressure distribution under the design condition and the velocity vector diagram of different blade height.
Ram Air Turbine,wilson theory,blade optimization design,NUMECA software,numerical simulation
北京高等学校高水平人才交叉培养“实培计划”大学生科研训练计划深化项目(项目编号:17032021006)空气悬浮鼓风机整机结构研制
2017-10-30 北京 102617
TK47;V43
1006-8155-(2017)06-0022-05
A
10.16492/j.fjjs.2017.06.0003

