赤松生长节律与降雨量关系研究

张靖，于凌飞，王一辰，张学勇，房克清,张德全

(1.山东省林业监测规划院，山东 济南 250014；2.山东省林木种质资源中心，山东 济南 250014)

气候变化是目前社会、经济、环境的重要问题之一，对于树木年轮的研究，对于揭示气候变化规律与机理起了不可替代的重要作用。但有许多人利用年轮资料与年降雨量资料的分析，得出年降雨量的变化对树木生长无显著性影响的结论，笔者认为他们得出的结论可能是出于个例，有可能数据观测的偏差(如假年轮的影响等)，也有可能年降雨量不是树木生长实地的资料所致，也有可能是其他噪声的综合影响的结果。笔者借助解析木数据资料，经过大量反复研究比对分析，呈现出十分惊人的规律性。根据高卫东(2011)等人的研究，他用年轮资料对过去338年(1666-2003)的天山北坡中部的年降水量进行了重建，指出存在明显干旱与湿润交替周期性变化现象。燕子杰(1991)将1470—1985年的516年山东气候变化分为干湿变化的5个阶段，年数分别为121，192，56，77，70，可见近期70年左右为一个气候变化周期，而且年变化年数有逐步缩短的趋势。由于林业经营周期长的特点，研究气候的周期变化特点，对于我们意义深远而重大。下面笔者就用解析木和有关年轮技术以牟平地区为例对山东气候周期性变化特点进行研究。

1 资料来源

历年降水量资料由烟台市牟平区气象局提供，解析木材料来自2013年3月中旬笔者采自烟台市牟平区昆嵛山林场两株，生长正常的赤松解析木分别为65年生和45年生，风云林场两株，生长正常的赤松解析木，分别为77年生和61年生。树高超过10 m的，胸径段用2.6 m区段，其他采用2 m区段，分别在树高5 cm(0盘)、1.3 m、3.6 m、5.6 m、7.6 m、9.6 m处截取圆盘；树高不到10 m的，采用1 m区段，5 cm(0盘)、1.3 m、0.5 m、1.5 m……9.5 m处截取圆盘。进行干燥(风干)、打磨，用高分辨率扫描仪进行彩色扫描，并将扫描好的图像放入CAD操作平台中进行量测，并用实测资料进行校正，分别量取南北径和东西径，并以5年龄阶进行交叉定年，数据精度为0.01 cm，量取各树盘各年度的树木直径，并根据有关测树学技术原理，推算树高和材积。

2 研究方法

经过笔者近10多年来的研究，树木的生长量、生物量、碳储量均与树龄及年降雨量之间表现出十分明显的相关关系，而且凡是线性相关系显著的，其对数值表现更为显著的相关性。经过笔者悉心研究，用指数经验方程Y=exp(a+bx)用来判断因变量y随自变量x的变化程度(变化速度)。其中y为树木的生长量、生物量、碳储量等指标，x为树龄及年降雨量等自然因素指标，a,b为待求系数(下同)。用混合经验方程y=exp(a-b/x)来寻求效益指标最大化，即用最少的投入(包括时间)以求获得最大的收益。笔者经过研究，通过以每一年为研究对象，对方程进行拟合试验，结果除个别指标表现出相关关系显著外，大部分指标相关关系不显著，但是通过累加效应(即用累计生长量与树木年龄、降雨量累加量等建立回归相关方程)，则表现出十分显著的相关性。笔者认为有许多研究人员用5年滑动的办法，使回归相关系数大大提高，事实上就用5年的数据累加，只不过是取了5年的均值而已，事实是这种做法只是提高回归精度的一种办法，其科学含义就不准确了，笔者采用累加效应具有十分明确的科学含义。例如树木生长量和树木年龄。年木年龄就时间的累加量，树木生长量累加，即树木总生长量。而用5年滑动的办法处理数据，是用5年的均值代表中间年份的数据指标，我认为是有点牵强附会，用5年滑动的办法，对于首尾两端的数据就不好处理了，因为缺乏数据支撑，但是对于研究上百年上千年的数据变化还是可以的，可以将两端数据舍弃。笔者充分利用累加效应，不仅弥补了滑动处理数据的不足，而且更能显示其科学含义，而且计算量相对小一点。

先用经验方程y=exp(a+bt)和y=exp(a-b/t)建立树木生长量与树木生长年龄的回归关系，求得待求系数，再用经验方程y=exp(a+bp)和y=exp(a-b/p)求得树木生长量与年降雨量的回归系数，再用树木年龄的回归方程计算结果对降雨量回归方程进行技术修正，所有过程均要进行检验和校验，然后用校验好的降雨量回归方程，对没有降雨量记载的年份的年降雨量进行重建，进而得出树木整个生长期的年降雨量，进而进行气候干湿周期的研究分析。具体研究过程在下面的章节中进行论述。

3 研究过程

经过研究发现，对于经验方程y=exp(a+bx)的演算，当x的所有数据同时加上或减去同一数值，试验结果只是a值变化，b值和用来检验的t值、F值、R值及试验精保持不变，因此通过这一方程，来实现以往没有实际记载数据的重建成为可能，而保持现试验的精度不变。

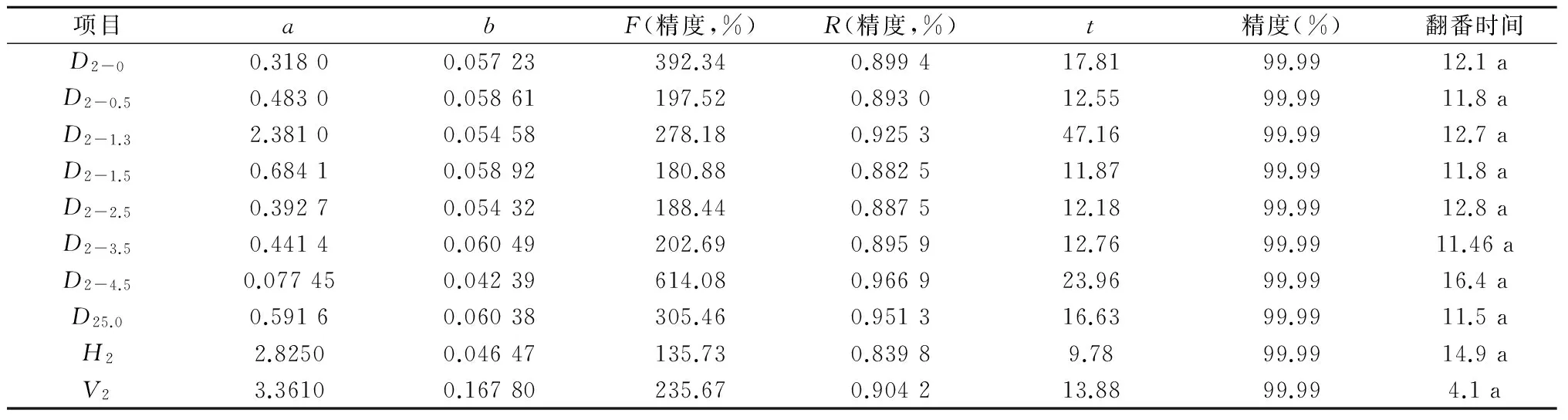
表1 77年生赤松生长过程经验方程拟合表(近42 a) Y(t)=exp(a+bt)

笔者以77年生样木为主进行论述，对这一科学研究方法进行论述。先用解析木资料建立树木生长量与树木年龄的经验方程。用D2-0代表地径项目，用D2-0.5代表0.5 m高处树径项目，余者类推，用H2代表树高项目，用V2代表树木材积项目。用Y(t)代表以时间(树木年龄)为自变量，以树木各种指标的生长量为因变量的函数。分别利用经验方程Y(t)=exp(a+bt) 和Y(t)=exp(a-b/t)建立数字回归方程。用电子表格计算，得到试验结果如表1～表4所示。所有项目均通过R检验、F检验和t检验，拟合精度均达到99.99%以上，表3的胸径(1.3 m树高处的树木直径)项目、表4许多项目研究精度无限接近100%。表中的翻番时间，为该树木生长量每增长一倍所需时间，用来形象地表达树木生长速度。从表1看出，树木材积增长最快，而表2中看出，树木5.0 m 径增长最快。表3、表4中的tm、tz分别为函数Y(t)=exp(a-b/t)的一阶和二阶导数值，前者是在此时刻树木生长指标平均增长速度最大，后者是即时增长速度最大，前者是后者的二倍。试验精度之高，说明笔者选用方法及试验数据的科学合理性和准确性。由于笔者进行了上百次的科学试验，均表现出方程的适合性，因此笔者不再做类似的适合性检验。

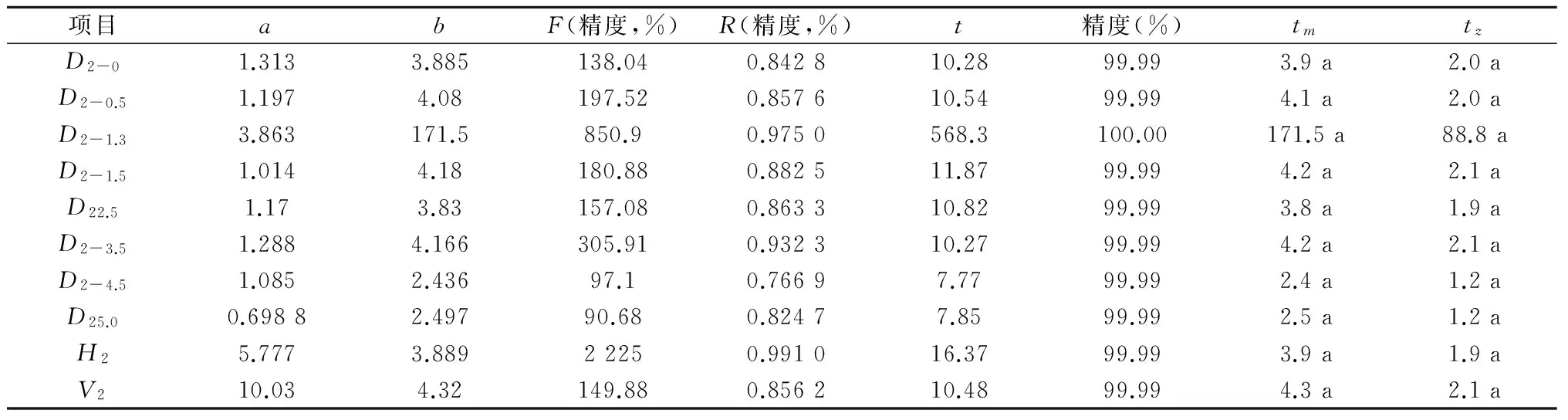
表2 77年生赤松生长过程经验方程拟合表(近42a) Y(t)=exp(a-b/t)

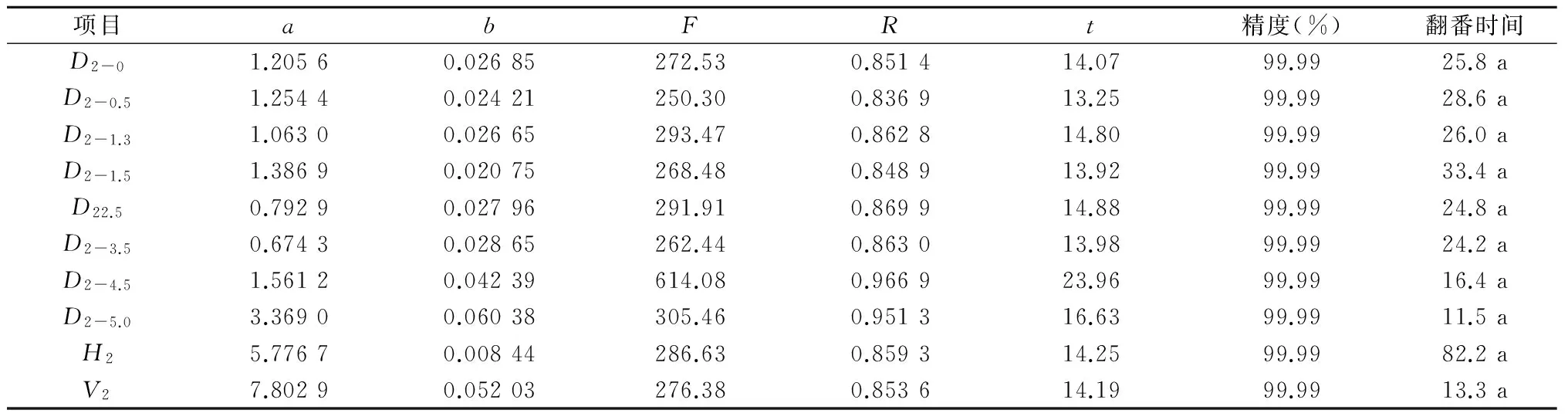
表3 77年生赤松生长过程经验方程拟合表Y(t)=exp(a+bt)

表4 77年生赤松生长过程经验方程拟合表Y(t)=exp(a-b/t)

以同样的方法进行赤松生长量与降雨量经验方程的拟合，拟合结果详见表5、表6。除表6中的D2-5.0项目拟合结果出现异常外，其余均具有一致性，说明拟合结果稳定可靠。

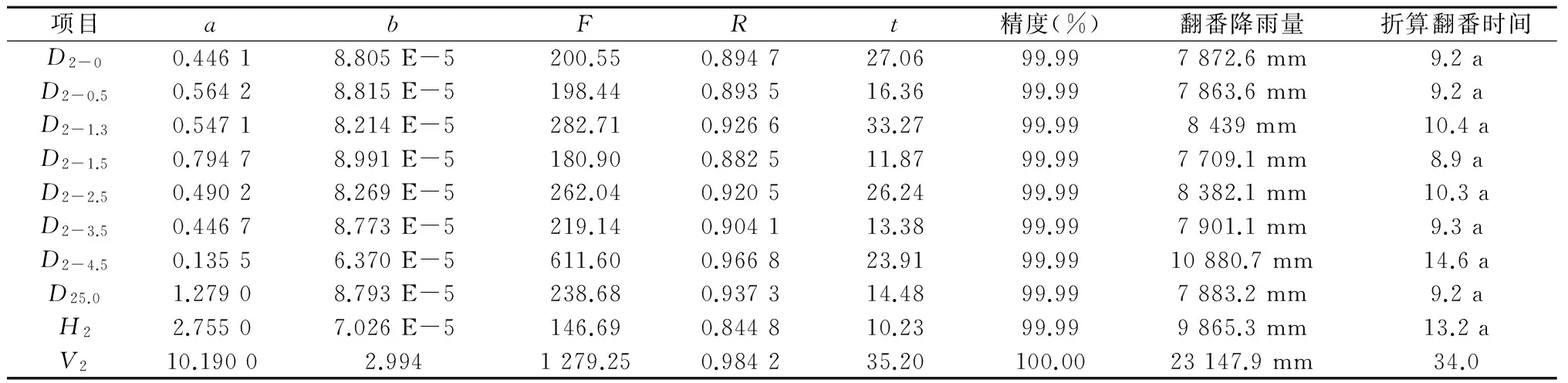
表5 77年生赤松生长量与降雨量经验方程拟合表(近42 a) Y(p)=exp(a+bp)

表6 77年生赤松生长量与降雨量经验方程拟合表(近42a) Y(p)=exp(a-b/p)

为了进一步提高本试验研究精度，以期求得降雨量相对于树木年龄的树木生长影响贡献率，对降雨量拟合经验方程进行校正，就是直接利用树木生长量的对数值与树木年龄经验方程拟合结果得出的树木生长量的对数差值为因变量，以降水量数据为自变量，重新建立经验方程进行拟合，拟合结果见表7、表8。

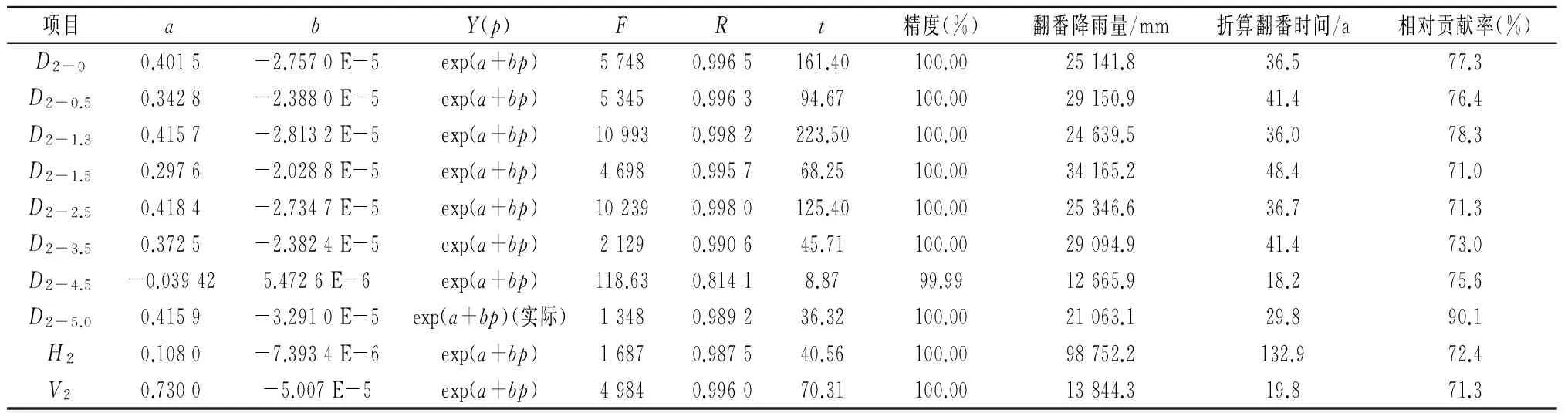
表7 77年生赤松生长量与降雨量经验方程拟合校正表(近42 a) (对数差值指数方程)

表8 77年生赤松生长量与降雨量经验方程拟合校正表(近42a)(混合函数方程)

表7是利用树龄指数经验方程的拟合结果的对数与树木生长量的对数差值为因变量Y(p)，表8是利用混合经验方程拟合结果进行同样的试验。由于由此得出的混合函数方程试验精度很低，笔者不再在表中列出，只有D2-1.5项目表现出接近100%的准确性，结果在表6中列出。笔者在校正试验中，只是列出试验精度相对较高的项目。从表中可以看出，试验结果除个别项目外，试验精度均无限地接近100%，因此可以付诸应用。从函数曲线的发展态势可以看出，由于所有研究指标的非负性，指数函数方程y=exp(a+bx)是研究y随x的增长的趋势，混合函数方程y=exp(a-b/x)是研究y随x的下降的趋势，由于笔者直接用的后近42年的降雨量数据资料进行的赤松生长量和降雨量之间的拟合试验，由于缺少前35年的降水量资料，而生长量又是整个年份的累加，因此出现了表7中的b值均为负值，翻番降雨量事实上也是负值，指的是下降一番(即下降50%)的降雨量，改为正值就是翻番降水量了。我再以表7中的D2-0项目介绍一下相对贡献率的计算。这里的折算翻番时间为36.5 a，可以理解为是扣除了树木生长曲线(S型)特性影响以后的数值，它与表中同一项目指标25.8 a的差值10.7 a，也就是树木本身生长特性比降雨量单独影响提高了10.7 a，笔者把25.8 a定义为降雨量单独影响所需翻番时间。由于增长速度和所用时间成反比例(倒数)关系，所以该项目的相对贡献率为1÷[1+(10.7÷36.5)]=77.3%。用同样的方法计算出其他项的想对贡献率。从计算结果可以看出降水量对树木生长量影响的相对贡献率，表7数值在71.6%～90.4%，表8数值在78.4%～91.9%之间，数值指标变化幅度不大，表现稳定，两表之间的数值相差10%左右，可能是由于研究精度的差别造成的，笔者认为表7的精度较高，可靠性大。因此降雨量对树木生长量影响权重达到80%左右，可见研究降雨量对树木生长量影响是何等的重要。

4 试验方程的适用性检验

笔者用同样的方法对另外三株样木进行了的试验，取得了较好的试验效果，以此3株样木试验结果对以上的试验结果进行适合性检验。检验结果如表9所示。表中FZ-1与FZj-1分别代表指数方程树龄因素校正前后与1号样木比较的F值，FH-1与Fhj-1分别代表混合方程树龄因素校正前后与1号样木的F值，D0代表地径项目,余者类推。

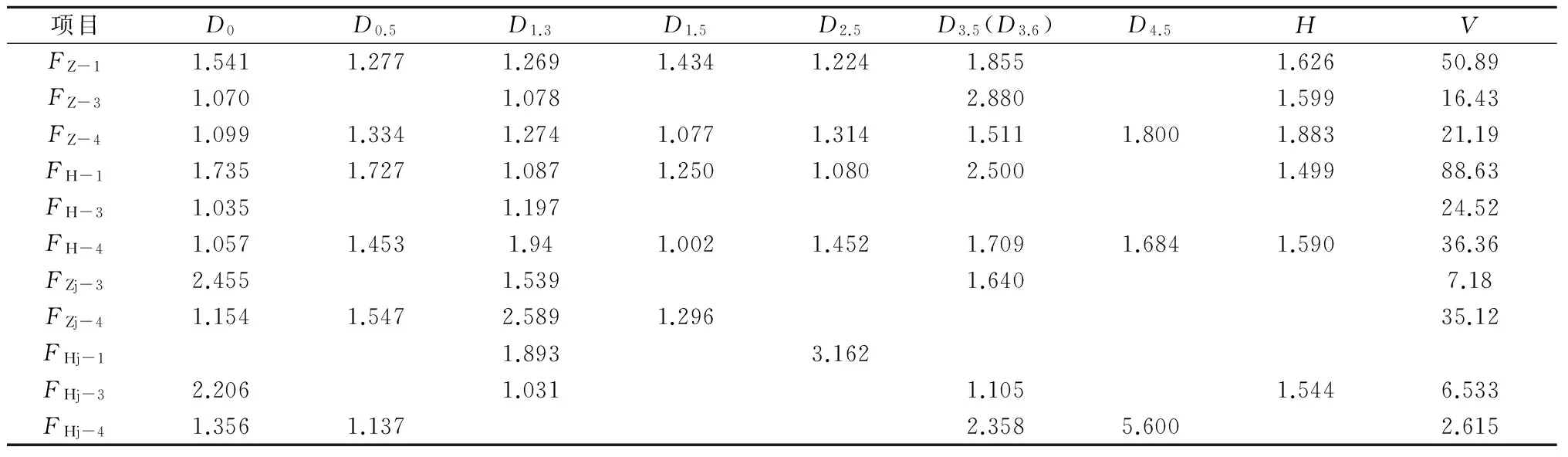
表9 经验方程适合性检验表

通过查表，从表9中可以看出，除材积未通过适应性验证检验外，其余均以较高的可靠性(95%以上)通过适应性验证，因此均可应用。检验结果表明，除了材积外，在缺少(或数量较少)年降雨量资料的条件下，可以借用本研究的经验方程，以求得该地的年降雨量数据。但是材积经验方程不能借用，必须在条件具备的条件下重新方程拟合试验，直到通过适应性检验为止。用同样的方法(从表9也可以看出)，同一样木的各项目之间的经验方程、指数函数方程与混合函数之间除了材积外，也均能通过适应性验证。为了获取更多的年降雨量数据，笔者主要应用地径、0.5、1.3、1.5、2.5 m径经验方程，和树高经验方程选其精度较高的。从表中观察分析以树高1.3～3.5 m之间取的树木圆盘数据资料，作的方程拟合试验精度较高，试验精度接近100%，回归系数达到0.99以上，与1非常接近了，达到了1就是完全回归了。

5 1939—1970年年降雨量重建与气候干湿周期

笔者利用以上建立的经验方程，利用树木后生长量数据，对年降水量进行逆运算，还原出1936-1970年牟平区年降水量数据。通过反复对比核算，发现校正后的方程得出的年降雨量数据，与已有的年降水量数据吻合性较好，而对于前35年降雨量重建意义不大，因为与实际差别较大，甚至出现年降雨量负值现象，这就是用同样树龄的树木生长量数据对历史上的年降雨量进行复原处理具有现实意义，对此需要另立课题进行研究。笔者利用表1中的D2-0与D2-0.5经验方程，对前35年的年降雨量进行重建，其他经验方程也进行了重建降雨量的试验，结果与现实相差较远，只有两个方程的试验结果比较接近现实情况，由于有记载的历史上的1939年特大洪水，上海《申报》曾以醒目标题报道了水患的广泛和严重性：“冀鲁豫等地，几成一片泽国，八十年来仅见之灾情，无家可归者数百万人。”1959—1961年特大干旱，两个方程的模拟结果，均得到了较好的印证，但是D2-0.5经验方程吻合程度更好一些。将该方程的试验结果列表10。

表10 1939—1970年降雨量重建表

笔者1939年为年降水量最大的年份，年降水量为2 744.8 mm，而年降水量最小的年份为1961年，仅有134.5 mm。表中年降雨量1930—1938的年均降雨量为D2-0方程的1936年的拟合值，由于林学理论认为前3年树木生长极不稳定，1936—1938年两方程除此之外数据均偏大，因而舍弃不用。表中均根据试验发展趋势，并根据相关历史资料对1928—1938年状况及2016年以后的发展态势进行了估测。笔者认为下一个气候湿润周期即将到来，一般在5年左右或更近一些时间，可能就会进入丰水期了，那将是绿化美化山东的绝好佳机，如果是有特大洪水的暴发，就请有关部门随时注意天气趋势预报，做好应急准备。这里需要说明的是常年值是利用1939—1970年的重建值和1971—2015年的气象年降水量数据的均值708.8 mm,较常年偏差就是以此为基础计算出来的。

7 讨论

笔者用模拟方程对树木生长量与降水量关系进行研究，开辟了一种崭新的途径。先前许多学者可能是由于测量不准确，收集数据较少的原因，而得出树木生长与降水量相关关系不明显的结论，只有做大量艰苦细致的工作，方能得出正确的结论。先前许多学者大部分是利用孤立的树干圆盘，利用年轮测量仪器对年轮宽度进行了测量，笔者是利用多个树木圆盘进行扫描，并在CAD状态下进行判读，利用实测数据进行校正处理，笔者认为本人所进行的试验更具有科学合理性，节省了研究成本的投入，起到了事半功倍的作用，笔者认为并不是试验数据小数点位数越多越好，因为年降雨量数据为4位有效数字，树木直径的测量保留4位有有效数字(即精确至0.1 mm)即可。有的学者精确至0.01 mm，如果是对于生长特别慢的红木等我认为是有必要的，但是对于其他树木就没有必要了，这样可以省下许多工作量，笔者在CAD状态下进行判读，可精确至小数点后若干位，为了节省工作时间，笔者只保留了4位有效数字。通过研究，科学回答了经验方程的科学含义，指数方程即呈指数增长，也就是递增的意思，是树木生长上升潜力的表达式，反映出树木生长的速度问题；而另一混合方程则是树木生长下行压力的表达式，它揭示了效益最大化问题。通过对树木自身增长潜力作用的剔除，而得到降水对于树木生长的相对贡献率，从增长潜力看，相对贡献率均值为75.7%，从增长的下行压力看，相对贡献率均值为83.5%，二者的中值为79.6%，这就是说树木的生长相对于树木生长特性来说，降水量对树木生长的影响起到80%左右的影响，树木本身特性仅占20%左右，因此研究降水量对树木生长的影响是何等的重要。通过验证经验方程具有实用性，可利用其他赤松等松类的年生长量数据对历史上的年降水量进行科学重建。通过对历史的年降水量数据进行重建以及现有的年降水量有关数据资料，通过对比分析当地气候变化存在明显的周期性，气候变化具有干湿周期性交替的特性，而且科学预见相对湿润的气候周期即将来临，对于我们合理组织林业生产具有深远的意义。

[1] 廉丽姝.山东近40年气候变化特征[J].气象科技，2006,34(1):57-59

[2] 高卫东.树木年停车费记录的天山北坡中部过去338 a降水变化[J].中国沙漠，2011,31(6):1535-1540

[3] 刘国杰.注册咨询工程师(投资)执业资格考试教材复习指导[M].天津：天津大学出版社，2003