辽宁抚顺落叶松人工林单木生物量回归模型分析

张士亮

(辽宁省林业调查规划院,辽宁 沈阳 110122)

生物量研究是林业科学研究的一项重要内容。单木生物量的回归模型建立是生物量研究的重要组成部分,是森林生态系统群落生物量估算的基础。目前生物量模型估算法是被应用最多的方法之一，该方法是首先通过调查得到一定数量的样木生物量的基础数据,然后利用林木易测因子如胸径和树高等进行回归分析来推算难于测定的林木生物量,最后选择合适的最优模型用于估算整个林分的生物量。这种方法建立的生物量模型在保证精度的同时，可以大大减少测定生物量的外业调查工作量。[1]模型建成以后,同类的林分就可以利用既有的资料来估计整个林分的生物量。本文以不同径阶的落叶松人工林为研究对象,构建落叶松人工林单木的各分量生物量模型。

1 研究区域概况

本次调查研究的区域为辽宁省国有抚顺县温道林场。温道林场位于抚顺市抚顺县东南部，上马乡境内。地理坐标为124°—124°8′ E，41°45′—51°53′ N。东临新宾县界，西接抚顺市市郊，南连后安镇，北靠大伙房水库，与伙房林场接壤。三面环山，一面靠水，自然条件较好。本区属温带季风型大陆气候，土壤主要为棕色森林土，结构疏松，肥力较好。本区属长白山脉龙岗支脉西麓的地山区，境内最高山峰海拔526.0 m，最低136.0 m，一般海拔200～300 m，属低山区，坡度为15°～25°，本区地处华北植物区系东北部的边缘地带，主要树种有落叶松、油松、红松、樟子松、刺槐、柞树、胡桃楸、椴树等。

2 研究方法

2.1 样木选取

本次研究共选取48株标准木(见表1、表2)。要求在具有典型特征的落叶松人工林内选取具有代表性、生长正常的落叶松作为标准木。

表1 标准木径阶—株数统计表

表2 标准木概况

2.2 林木生物量测定

对标准木进行每木检尺，并测定胸径,伐倒后测树高， 根部采用全挖法处理， 对标准木进行树干解析，测各器官〔干(含皮)、枝、叶、根〕鲜质量,每株标准木的各器官均取1份500 g的样品，装入布袋并标记后,带回试验室在85 ℃恒温下烘24 h至恒质量，然后用电子天平称质量， 利用称质量后得出的数据计算样品含水率,换算各组分的干生物量。根据实测各树种标准木的胸径、树高，以及通过试验室测得的各器官干生物量进行了统计分析。

2.3 数据处理

利用SPSS及Excel进行数据分析与处理。比选出无论是对不同器官的生物量还是树木总生物量拟合效果最好的模型。然后根据确定的模型拟合出树木各器官生物量和树木总生物量回归方程。

2.4 模型检验

应用检验数据及文中所建的模型计算出下面的统计值来对模型进行独立性检验。

总相对误差：

平均相对误差:

平均相对误差绝对值:

预估精度：

其中：yi为实测值，yi^为估计值，n为样本数，m为回归模型中的参数个数，Ta为置信水平a(0.05)时的T分布值。

3 生物量预测方程的建立

3.1 变量的设定与选取

关于立木生物量模型的建立,模型自变量可选用不同的变量,例如:D、D2H、冠下径、冠幅、树冠体积、树冠表面积等。[2]但大量的研究表明，林分的胸径和树高仍是生物量建模最主要的测树因子。本研究就是以胸径和树高作为基本因子,来对落叶松人工林的各部分生物量进行预测。

3.2 模型的确定

分别以胸径(D)、胸径—树高(D2H)为自变量,用直线回归(Linear模型)、对数回归(Logarithmic模型)、逆矩阵(Inverse模型)、二次方程(Quadratic模型)、三次方程(Cubic模型)、复合曲线(ComPound模型)、幂回归(Power模型)、S形曲线(S-curve模型)、生长曲线(Growth模型)、指数回归(Exponential模型)、Logistic曲线(Logistic模型)等11种数学回归模型计算分析，拟合出11种模型的树木器官生物量和总生物量的回归方程(表3)。

(1)Linear模型，拟合直线方程，即直线回归，模型表达式为：

Y=a+bx

(2)Logarithmic模型，拟合对数方程，模型表达式为：

Y=a+blnX

(3)Inverse模型，拟合逆矩阵，模型表达式为：

(4)Quadratic模型，拟合二次方程，模型表达式为：

Y=a+bX+cX2

(5)Cubic模型，拟合三次方程，模型表达式为：

Y=a+bX+cX2+dX3

(6)ComPound模型，拟合复合曲线，模型表达式为：

Y=abX或 lnY=lna+Xlnb

(7)Power模型，拟合乘幂曲线，模型表达式为：

Y=aXb或 lnY=lna+blnX

(8)S-curve模型，拟合S形曲线，模型表达式为：

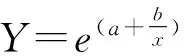
(9)Growth模型，拟合等比级数曲线，模型表达式为：

Y=e(a+bX)或 lnY=a+bx

(10) Exponential模型，拟合指数方程，模型表达式为：

Y=aebX或 lnY=lna+bX

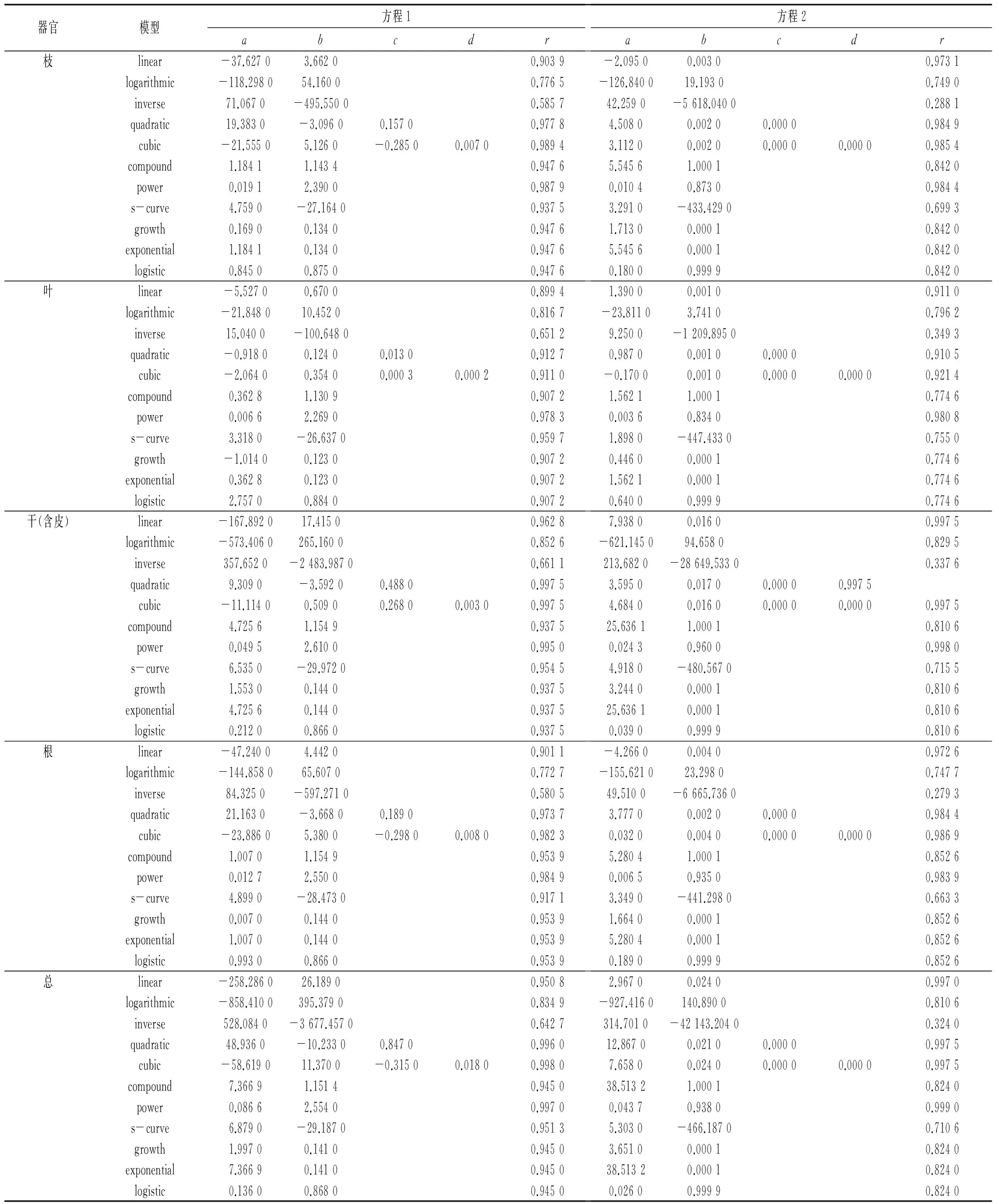
表3 11种数学模型拟合的单木生物量方程

注：1)a、b、c、d—模型参数，r—相关系数;2)方程1中，模型因变量Y=W，自变量X=D，W—生物量，D—胸径;3)方程2中，模型因变量Y=W，自变量X=D2H，W—生物量，D—胸径、H—树高;4)经检验，所有相关均显著

(11) Logistic模型，拟合Logistic曲线，模型表达式为：

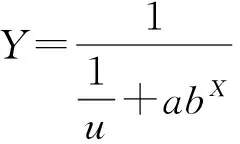
上述11中模型公式中,Y为因变量，X为自变量,a、b、c、d为模型参数。

计算分析结果表明各函数模型均达到相关显著水平。从上面的数据分析可以看出,计算与分析效果最好的是Power模型(幂回归)，该模型无论是对各树种不同器官的生物量还是树木总生物量的拟合效果均较好，适用性非常强。[3]

分别以D，D2H作为自变量，W作为因变量，(lna=a′)拟合出两种形式的树木各器官生物量和树木总生物量回归方程(表4),为计算方便和从形式上更为直观地表达Power模型的拟合结果，表达形式分别为:

lnW=a′+blnD

lnW=a′+bln(D2H)

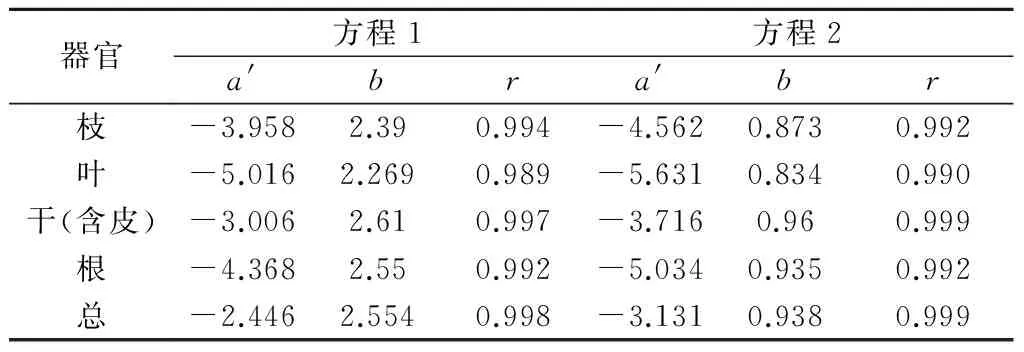
表4 2种形式的单木生物量方程

注：经检验，所有相关均显著

3.3 模型的验证

应用检验数据,对本文所建立的单木各生物量模型进行验证和评价,计算各种检验统计量,结果如下(表5)：

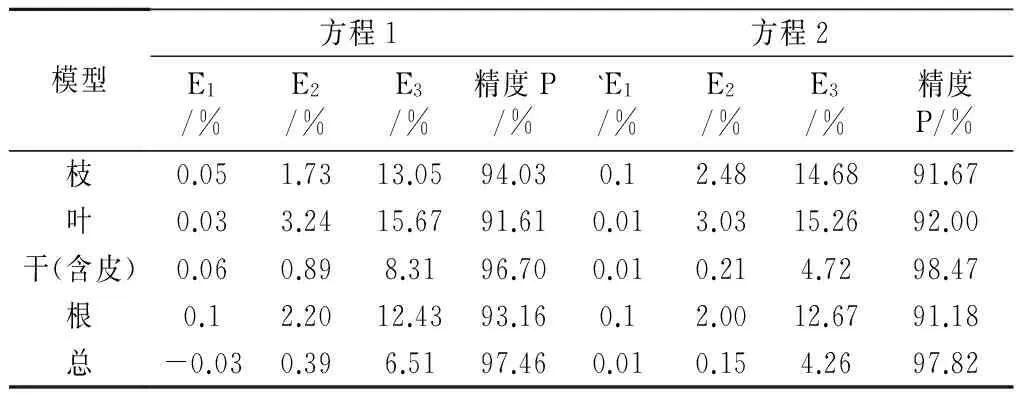
表5 2种形式的单木生物量模型检验结果

从表5的检验结果来看，各组分生物量模型的总相对误差值均在±1以内；预测精度P均达到了90%以上；各组分生物量模型的平均相对误差均在5%以内，说明所建立各分量生物量模型无系统偏差。从平均相对误差绝对值指标上看:全树重、干、枝、根和叶其幅度范围为4.26%～15.67%；参数的变动系数和统计指标各树种规律是一致的，对各组分生物量模型的预测效果进行排序则为：总量>树干>根系>树枝>树叶，即对总量的预测效果最好，其次是树干，再次是根系，然后是树枝，树叶的预测结果效果最差，这也验证了之前专家学者的研究结论。造成这种现象的主要原因是树木各组分的抗干扰性造成的，相比较树干的结构稳定性最好，最不容易受外界影响，而树冠部分生物量受树冠形状、大小和饱满程度以及树木长势影响很大,而这些因素是随气候、环境不同而变化的,因此就造成了树冠部分生物量特别是叶生物量变动范围很大。

3.4 标准木生物量分配规律

落叶松人工林单木生物量随着林木生长而增大，不同径阶落叶松标准木各器官的生物量所占总生物量的百分比出现明显变化，从图1可以看出，在不同径阶的落叶松中，各器官的生物量均以树干为最高，比重均能达到60%以上，且随着胸径的增加，其所占比重明显升高，与树干的变化趋势相反，树枝和树叶的比例随着胸径的增加而出现明显下降，而树根所占比重随胸径增大而略有下降，但极不明显。

图1 标准木生物量比例分配趋势图

4 结论和建议

4.1 最优方程

通过大量的内外业调查分析，落叶松人工林各分量生物量估计的最优方程为：

枝生物量的最优方程为：lnW=-3.958+2.39lnD；

叶生物量的最优方程为：lnW=-5.631+0.834ln(D2H)；

干生物量的最优方程为：lnW=-3.716+0.96ln(D2H)；

根系生物量的最优方程为：lnW=-4.368+2.55lnD；

全株生物量的最优方程为：lnW=-3.131+0.938 ln (D2H)。

结果表明，除树枝和树根外，其他器官的生物量回归模型和总生物量的回归模型，均以自变量D2H建立的回归方程为佳。

4.2 检验估计的模型结果

各组分生物量模型的总相对误差值均在±1以内；预测精度P均达到了90%以上；各组分生物量模型的平均相对误差均在5%以内，说明所建立各分量生物量模型无系统偏差。对各组分生物量模型的预测效果进行排序则为：总量>树干>根系>树枝>树叶。

4.3 生物量分布规律

在不同径阶的落叶松中，各器官的生物量均以树干为最高，且随着胸径的增加其所占比重明显升高，树枝和树叶的比例随着胸径的增加而出现明显下降，而树根所占比重随胸径增大而略有下降，但极不明显。

4.4 建议

结果表明，构建的总生物量回归方程的相关系数在0.99以上，预测精度在95%以上，利用本文所建立的生物量模型可很好的对辽宁东部山区的落叶松人工林单木生物量进行估计，实用价值极高。

[1] 田杰,于大炮,周莉,等.辽东山区典型森林生态系统碳密度[J].生态学杂志,2012，31(11):2723-2729

[2] 贾炜玮，于爱民.樟子松人工林单木生物量模型研究[J].林业科技情报,2008,40(2):1-2

[3] 程堂仁.甘肃小陇山森林生物量及碳储量研究[D].北京：北京林业大学,2007