记录扰动场的二维山包绕流的数值分析

任超洋，陈善群，廖 斌，吴 昊

(安徽工程大学， 安徽 芜湖 241000)

记录扰动场的二维山包绕流的数值分析

任超洋，陈善群，廖 斌，吴 昊

(安徽工程大学， 安徽 芜湖 241000)

首先采用k-ε模型对二维山包绕流进行试算，并拿计算结果与实验结果相比对，发现数值模拟与实验结果基本一致。验证完计算方法后在充分发展入流段加入X方向和Y方向两种不稳定的扰动场，经过计算之后用其结果对比实验数据，发现数值模拟与实验结果相差较大，在X方向加入扰动场之后发现漩涡出现后移现象，加入Y方向的扰动场之后，漩涡也出现了脱离山包顶端的现象，而且加入扰动场之后的漩涡中心位置也发生了较大变化。由于在现实中山包入流处的流速并非单一的，加入扰动场之后的计算结果为实际山地工程提供了数值依据。

山包绕流；k-ε模型； 扰动场； 数值模拟

当来流经过山地区域时，由于地形的影响，会导致一些不同情况的绕流现象出现。由于山地情况的不同，所产生的压力、风速情况也会有所不同，再加上目前城市化发展较快，平原地区已基本成为开发上的稀缺资源，现在建设已有向山地方向发展的趋势。在山地发展中多景区建设，并且存在着由于风的影响而导致的种种问题，自然界的风有时候并不是单一的朝一个方向吹来，有必要在进行数值模拟(CFD)的时候加上一些不稳定的扰动场。在研究山包绕流这一课题方面，国内外有许多学者在这方面做过很多的工作，Taylor等[1]在山坡、山脊的风速加强方面根据单个山丘的风洞试验结果提出了加速比(S)的简化公式，但并未考虑复杂山地形式带来的影响； Almeida等[2]对二维多项式型形状的单山包和多山包进行了绕流测速，其检测条件是在充分发展管道流利用多普勒激光测速仪(LDV)进行的，得到特殊断面上速度、雷诺应力的实验值； Weng等[3]通过对一系列形状为正弦曲线的连续分布二维山脊的边界层风场的湍流研究，得到的结论是孤立山丘的风速加速比高于复杂地形的风速加速比； Jackson等[4]提出了一种关于计算二维低矮小山包风速增大系数的解析式，此解析式是在基于线性理论而未考虑流动分离的前提下提出的； 陈善群等[5]通过运用标准k-ε模型、重整化数群k-ε模型(RNGk-ε)和雷诺应力模型(RSM)对二维单山包和多山包绕流进行了数值模拟，确定了数值模拟对于山地数值模拟的可行性。Bowen等[6]对不同坡度角的风坡面影响进行了详细的研究，对前人的实验结果进行了验证。魏慧荣[7]和康顺[8]通过利用软件NUMECA，模拟了三维山包风场，提出了预估风电场的新方法。但由于自然界的风流动并非单一的，在很多情况下都存在扰动的现象，以上学者都没有在山包流的入流处加上扰动场。

本文利用标准k-ε模型对2维山包进行验算，并与文献[2]进行对比，先验证此数值方法的可行性，然后在数值计算中加入不同方向和速度的流场扰动，最后拿计算结果和前面的标准k-ε模型计算结果进行对比，得出绕流场对于2维山包模型的影响。

1 数值方法与控制模型

1.1 数值方法

对于复杂的湍流运动使用描述湍流的瞬时运动的非稳态的连续方程和Navier-Stokes方程，其中Navier-Stokes方程可以用于计算二维山包绕流的不可压缩湍流流动，基于雷诺平均的动量方程和连续性方程在笛卡尔坐标系下可以表示为：

(1)

(2)

1.2 控制模型

利用Fluent15.0的分离求解器可以求得本文山包周围的流场，采用k-ε模型中的雷诺应力项进行模块化求解，壁面区域(Wall)采用标准壁面函数计算并处理； 利用目前工程上最为通用的SIMPLE算法计算离散形式的动量方程，最后得出速度场，速度场可用下述方程表示：

(3)

(4)

计算时采用2阶格式对动量、湍流动能、耗散率和雷诺应力进行求解，先假设一个速度分布，再假定一个压力场，分别用来计算迭代时的动量离散方程中的系数和常数项，接着求解k-ε方程，等到迭代收敛后得到速度和压力场，然后继续循环得到计算结果。

2 数值模型建立与计算条件设置

2.1 数值模型建立

本文所建立的2维山包形状如文献[2]所示。山包左右对称，最大高度H=28 mm，宽度为108 mm。坐标轴x=0位于山包的对称轴处，模型的底部位于y=0处，整个区域的数值计算长度为 1 100 mm，高度为170 mm，在山包上游给了 300 mm的来流发展入口，流体出口处为山包下游800 mm处，如图1所示。计算区域中流体密度为ρ=1 000 kg/m3，运动黏性系数ν=1.0×10-6m2/s。设置扰动场为来流发展区域山包前300 m处上半部分区域，如图2阴影区域所示，取两个方向的扰动场速度，分别是0°，90°两个方向，两个方向上速度均设置为150 m/s。本文网格在底边上设置了边界层，整个边界层从底边上开始，其中第一层网格大小根据对雷诺数的计算得到0.001 mm，最后将设得的边界层延伸到和网格尺寸一样大的时候即可，一共设置50层，设置边界层的好处就是可以增加网格的密度，从而提高计算精度，局部边界层如图3所示。

图1 模型简图

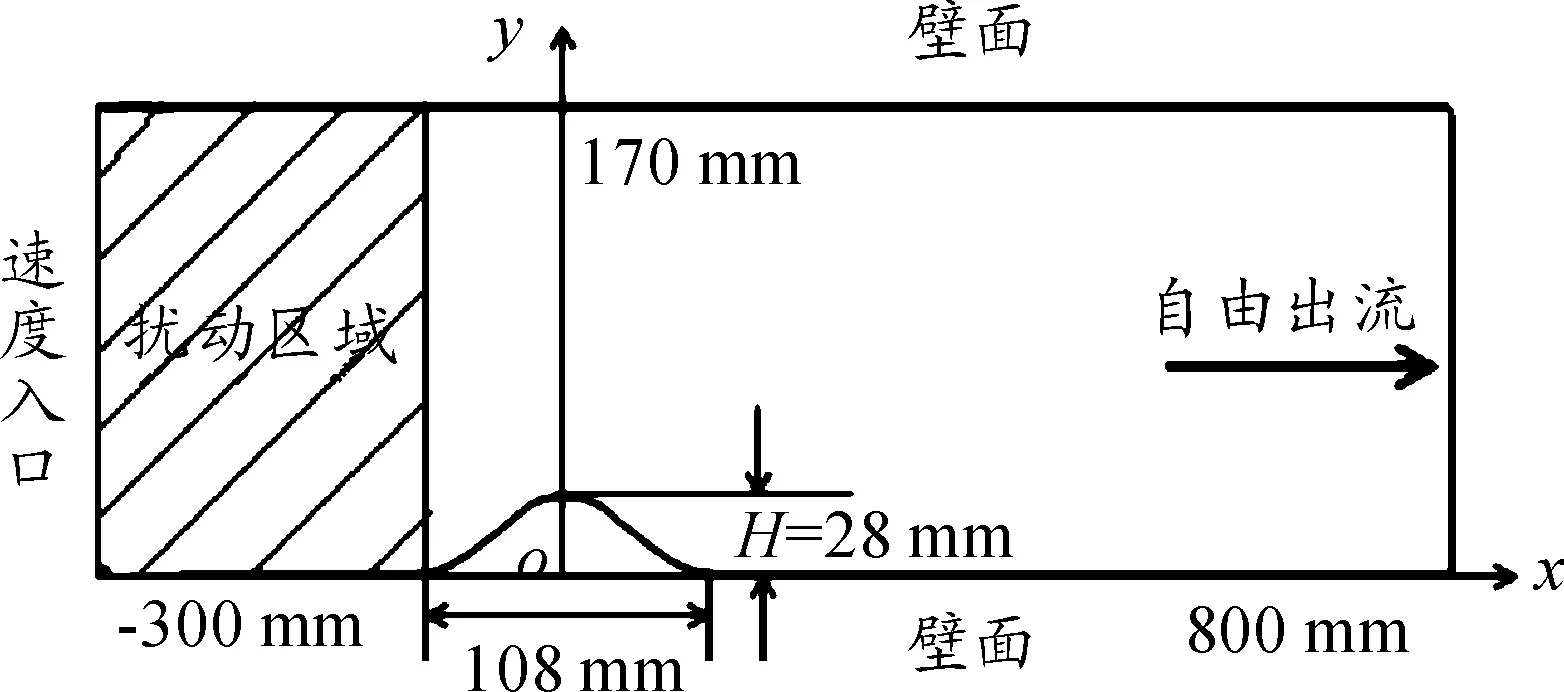
图2 扰动场示意图

图3 边界层示意图

2.2 计算条件设置

选择充分发展管道流为入口来流，以U0=2.147 m/s为管道中线处的平均流速，计算区域中的最大雷诺数Remax=60 000。将文献[1]中实验的入口断面流速拟合后呈指数型分布：

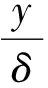
(5)

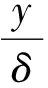
(6)

其中δ=0.5×ymax。

入口来流的湍流动能呈线性分布：

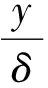
(7)

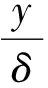
(8)

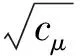
2.3 扰动场方程

在不同的高度或不同的位置会导致风场的一些差别，在实际工程中对于风场而言要复杂于数值模拟的情况。扰动场可用数学模型来表示，用计算时的量纲一时间平均分解成空间的平均量和扰动量，可以用下面两式表示：

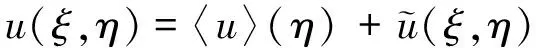
(9)

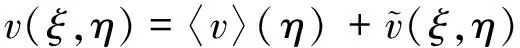
(10)

3 数值验证与加入扰动结果分析

3.1 数值验证

本文先通过对2维山包进行数值验证，通过观察速度矢量图，如图4所示，发现在山包后产生了一个类似椭圆形的顺时针旋流区域，并且可以发现速度在山包顶端靠后一侧有一个集中点，与实验结果基本吻合。分别对2维山包3个断面的X和Y方向的速度进行对比分析，图5中分别给出了X=0 mm，X=90 mm，X=120 mm 3个断面的数值对比分析图，分析的对象分别为水平速度的量纲一U/U0、垂直速度的量纲一V/U0，其数据与实验数据存在一些误差，但发展趋势基本吻合。

图4 速度矢量图

图5 3个断面的速度数据对比

3.2 加入扰动结果分析

通过图6可以看出：当在来流充分发展入口处加上一个X方向V=150 m/s的扰动场时，其速度分布出现了变化，原来在山包后面的椭圆形的漩涡区往后移动了102 mm，整个速度矢量场可以看出有明显的速度分层，在山包后方的漩涡区域的右上方出现了一个不对称的速度较高的集中区域。通过图7可以看出：当在来流充分发展入口处加上一个Y方向V=150 m/s的扰动场时，其速度又出现了新的变化，原来山包后面的椭圆形漩涡区域没有向后移动，这次产生的漩涡区域的右边没有紧贴山包的上部，其是从山包右端的中部开始向右发展。没有像加入X方向扰动场那样出现速度分层，出现了以流场区域X轴方向的中轴线为对称轴并且与漩涡区域对称的一个速度较高的集中区域。对加入两个方向扰动场之后的计算结果分别取X=0 mm，X=90 mm，X=120 mm这3个断面的数据进行分析，分析的对象还是水平速度的量纲一U/U0、垂直速度的量纲一V/U0，如图8所示。通过加入扰动场之后的速度数据折线图可以看出：加入扰动场之后对原来流场的影响很大。通过流线对比图可以看出：涡心位置有明显变化，如图9所示，图中未加扰动的漩涡区中心点坐标是(71.5,14.2)，图中加了X方向扰动场的漩涡中心点坐标是(296.1,36.8)；通过和未加扰动场的涡心位置对比，其涡心位置在X方向上产生了较大位移，为224.6 mm，在Y方向上位移较小,为22.6 mm； 图中加了Y方向扰动场的漩涡中心点坐标是(150.7,9.9)，在X方向上产生了位移，为79.2 mm，但是Y方向上产生了负位移,为-4.3 mm。

图6 X方向加入扰动速度矢量图

图7 Y方向加入扰动速度矢量图

图8 加入扰动之后的速度对比

图9 流线对比

4 结论

本文通过对2维山包进行数值模拟(CFD)，首先根据实验，验证对比本篇所采用数值方法的可行性与可靠性，然后对模型加入一个不稳定的扰动场并进行数值模拟计算，最后得出以下结论：

1) 根据计算结果来看，利用数值模拟(CFD)可以得到与其实验非常相似的结果，证明了数值模拟(CFD)在解决实际问题中的可行性。给计算模型加上边界层可以提高计算结构的准确性。

2) 加上不稳定的扰动场之后，其数值模拟(CFD)的结果与实验结果相差很大，而在自然界中，由于地理因素和周围环境因素，大部分的风场都是不稳定的，在对山地进行数值模拟时加上一段不稳定的扰动区域可以使计算得到的结果更加符合实际，为实际工程提供了数值计算依据。

3) 加入扰动场之后会导致涡心位置的偏移，也会导致漩涡区域大小的变化。

[1] TAYLOR P A,LEE R J.Simple guidelines for estimating wind speed variations due to small scale topographic features[J].Climatological Bull,1984,18(2):3-22.

[2] ALMEIDA G P,DURAO D F G,HEITOR M V.Ercoftac Classic Collection database,EXP.C18[DB/OL],http:// cfd.me.umist.ac.uk/ercoftac.

[3] WENG W,TAYLOR P A,WALMSLEY J L.Guidelines for air flow over complex terrain:model developments[J].J wind Eng Indus Aerodyn,2000,86:169-186.

[4] JACKSON P S,HUNT J C R.Turbulent Wind Flow over a low Hill,Quart[J].Jour of Royal Met Soc,1975,101:929-955.

[5] 陈善群，廖斌.单山包和多山包绕流的数值模拟研究[J].水利水电技术，2011(12):231-235.

[6] BOWEN A J,LINDLEY D A.Wind-Tunnel Investigation of the Wind Speed and Turbulence Characteristics Close to the Ground over Various Escarpment Shapes[J].Bound.Layer Meteorol,1977(12):259-271.

[7] 魏慧荣，康顺.风电场地形绕流的CFD结果确认研究[J].工程热物理学报,2007，28(4)：577-579.

[8] 康顺，魏慧荣.应用CFD于风电场风速分布预估的可行性探讨[J].工程热物理学报,2008，29(12):2040-2042.

NumericalAnalysisof2DParabolicFlowinRecordingDisturbanceField

REN Chaoyang, CHEN Shanqun, LIAO Bin, WU Hao

(Anhui Polytechnic University, Wuhu 241000, China)

We first use thek-εmodel to test the 2D parabolic flow, and compare the results with the experimental results. It is found that the calculated results are in good agreement with the experimental results. After verifying the calculation method, adding two kinds of unstable disturbances with theXdirection and theYdirection in the full development of the inflow section. After the calculation, the experimental data were compared with the results, and it found that the experimental results are different from the numerical simulation. After adding the disturbance field in theXdirection, it is found that the vortex appears to move backward. After adding theYdirection of the disturbance field, it is found that the whirlpool appeared from the top of the mountain. Due to the reality that the mountain bag into the flow rate is not single, and the results of this article after adding the disturbance field provide the numerical basis for the actual mountain engineering.

parabolic flow ;k-εmodel; disturbance field; numerical simulation

2017-07-07

安徽省2017年度高校优秀青年人才支持计划项目(gxyq2017015)

任超洋(1991—)，男，安徽芜湖人，硕士研究生，主要从事计算流体力学研究，E-mail:2906510498@qq.com; 通讯作者 陈善群(1981—)，安徽合肥人，博士，主要从事计算风工程研究，E-mail:chenshanqun@126.com。

任超洋，陈善群，廖斌，等.记录扰动场的二维山包绕流的数值分析[J].重庆理工大学学报(自然科学)，2017(12):88-93.

formatREN Chaoyang, CHEN Shanqun, LIAO Bin,et al.Numerical Analysis of 2D Parabolic Flow in Recording Disturbance Field[J].Journal of Chongqing University of Technology(Natural Science)，2017(12):88-93.

10.3969/j.issn.1674-8425(z).2017.12.015

O368

A

1674-8425(2017)12-0088-06

(责任编辑何杰玲)