非粘接柔性立管抗拉和抗扭刚度计算分析方法对比

裴晓梅， 张恩勇， 李丽玮， 周巍伟， 曹 静

(中海油研究总院，北京 100028)

非粘接柔性立管抗拉和抗扭刚度计算分析方法对比

裴晓梅， 张恩勇， 李丽玮， 周巍伟， 曹 静

(中海油研究总院，北京 100028)

针对非粘接柔性立管抗拉和抗扭刚度计算方法进行对比。以300m水深8英寸(1英寸≈2.54cm)非粘接柔性立管为例，首先介绍了立管截面设计时计算两种刚度所使用的理论计算方法，之后在理论计算的基础上，对非粘接柔性立管进行有限元分析，分别对比了非粘接柔性立管在轴向拉力及扭矩作用下的抗拉和抗扭刚度的计算结果，并对各层结构的刚度贡献情况进行了讨论。最终得出结论： 柔性立管在轴向载荷和扭矩作用下，理论计算结果与有限元计算结果较为一致，在抗扭刚度计算中理论计算结果更偏保守。在实际工程设计中，可以根据设计阶段选择合适的计算方法。

非粘接柔性立管；抗拉刚度；抗扭刚度；接触

0 引 言

为了防止结构失效，立管在设计阶段需要进行严格的分析计算和测试。立管结构在海面上主要承受较高的循环张力载荷，而在海底主要承受较大的外压、轴向压缩、弯曲以及扭转组合载荷[1]。同时，非粘接柔性立管(软管)由不同的层组成，从内往外包括骨架层、聚合物材料的内部水密层、互锁结构形式的抗压铠装层、耐磨层、两层抗拉铠装层和外部水密层，各层都有不同的功能作用[2]，各层间可以自由地相互滑动。柔性立管的刚度计算是截面设计中的重要环节，是关乎后续整体分析准确性的重要参数。根据理论计算公式和ABAQUS软件有限元分析，本文针对300m水深8英寸(1英寸≈2.54cm)输油软管，分别对柔性立管抗拉和抗扭刚度进行计算和对比，并对各层结构的刚度贡献情况进行了讨论。基于本文研究结果，在实际工程设计中，可以根据设计阶段选择合适的计算方法。

1 分析对象参数

图1所示为典型的非粘接柔性立管的各层结构。

图1 典型的非粘接柔性立管结构Fig.1 Inner structure of a typical unbonded flexible riser

以300m水深8英寸输油软管为例，立管共有16层，各层主要参数如表1所示。

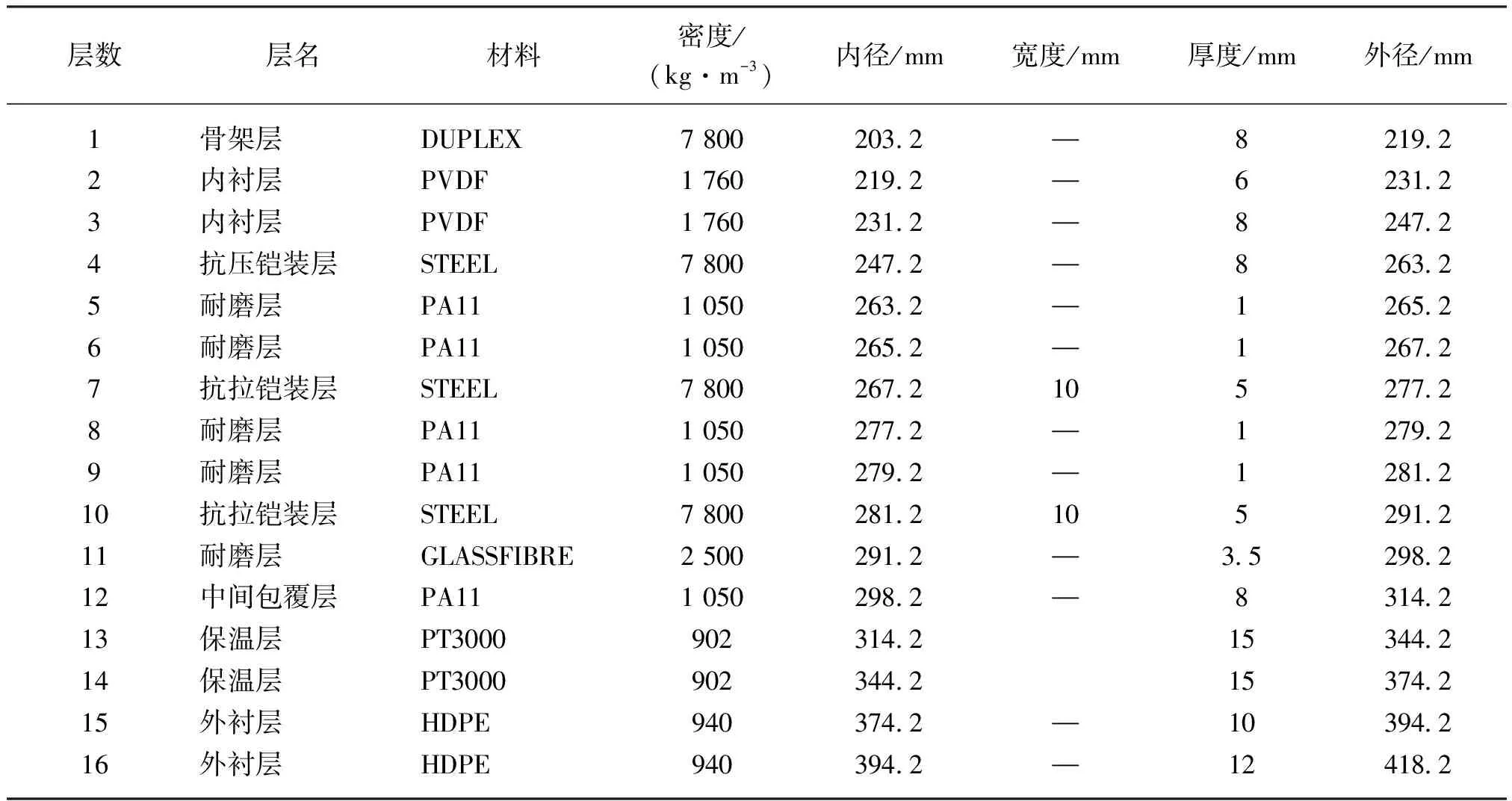
表1 8英寸输油软管各层参数Table 1 Layer properties of the 8 inch production riser

其中骨架层旋转角度为88°，抗压铠装层为89°，抗拉铠装层角度分别为35°和-35°。

2 分析方法介绍

目前针对非粘接柔性立管刚度的计算分析方法主要有两类： 理论计算法和有限元计算法。

理论计算法中所依据的解析方程主要来自柔性软管设计和操作手册[3]，此手册来源于针对柔性软管开展的研究项目(FPS 2000)成果报告，手册中提供了软管刚度计算公式，比较适用于前期设计阶段中软管刚度的快速计算。由于计算公式基于众多假设，在后续迭代计算中需要与有限元计算相结合，并采用试验验证计算结果。

对于多层柔性立管的有限元计算，目前有两种方法： 传统的等效梁法和多层法[4]。前者采用一个等效的梁单元模型，通过赋予等效截面属性和材料属性来进行分析计算[5]。这种方法的优点在于模型简单，节省计算时间；缺点是无法对立管内部各层的受力及相互作用进行计算和模拟。而柔性立管多层模型的有限元计算分析，则可以弥补等效梁方法的不足，可以模拟层与层之间的接触以及立管层与层间的摩擦和相对滑移，也可以考虑内外压力的影响。

3 理论计算方法

3.1 抗拉刚度

在柔性立管受拉力作用时，主要由螺旋缠绕的抗拉铠装层承担抗拉作用。聚合物层(内衬层、中间包覆层、外包覆层)在拉力作用下对刚度影响不大，在评估柔性立管抗拉性能时忽略其影响。

假设螺旋缠绕线为n层，铠装层内应力与拉力关系计算公式为

(1)

式中：ni为i层内铠装线数量；σi为i层内铠装线应力；Ai为i层内铠装线横截面积；αi为i层内铠装线角度。

由于抗压铠装层旋转角通常近似为90°，从式(1)可以看出，抗压铠装层对平衡轴向载荷影响甚微。因此，轴向载荷主要由抗拉铠装层承担。

假定拉力由每一条钢线平均分担，由轴向载荷引发的应力可由下式计算：

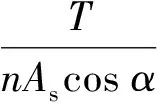
(2)

式中：As为单根抗拉铠装层钢线横截面积，等于宽度与厚度的乘积。

当柔性立管受到拉力载荷作用时，拉力会造成轴向变形(延伸)，内外压会引起径向变形(横截面积变大或变小)，而横截面会有旋转趋势，旋转变形与其他方向的变形相比通常非常小，忽略不计。抗拉铠装层钢线应变与这些变形之间的关系可以写作

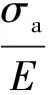
(4)

ν为直径减小引起的轴向延伸，可以得到

T=nEAscosα(cos2α-νsin2α)εxx.

(5)

因此，柔性立管轴向刚度可以写作

EA=nEAscosα(cos2α-νsin2α).

(6)

由于抗拉铠装层钢线为多层，表达式可写作

(7)

上式基于小几何变形的假设，并且假设在变形过程中各层始终保持接触。

抗拉铠装层的内径和厚度确定后，抗拉刚度主要由抗拉铠装层钢线决定。由于抗拉层材料的杨氏模量要比热塑层大得多，因此热塑层的影响忽略不计。

3.2 抗扭刚度

在计算抗扭刚度时，可以同时考虑聚合物层和金属螺旋层的贡献。在考虑聚合物层时，其对扭转刚度的贡献可采用以下公式：

(8)

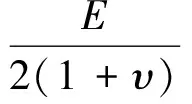
(9)

(10)

式中：Gi为某一层的剪切模量；E为杨氏模量；υ为材料泊松比；doi为聚合物层i层外径；dii为聚合物层i层内径。

由于金属螺旋铠装层的杨氏模量与聚合物层相比大得多，扭转力矩主要由螺旋铠装层承担，故忽略聚合物层的影响。而骨架层与抗压铠装层作为互锁层，缠绕角度太大，对抵抗扭矩贡献不大，因此主要由抗拉铠装层抵抗扭矩。

扭矩与在螺旋铠装层中应力的平衡公式可写作

(11)

式中：Mt为扭矩；ni为i层中铠装线数量；σi为i层中应力；Asi为i层中铠装线横截面积；ri为i层平均半径；αi为i层旋转角度。

假设抗拉铠装层中所有铠装钢线的形状均相同，公式可写作

(12)

忽略轴向和径向应变，应力与扭转应变之间的关系为

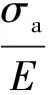
(13)

结合以上两式，可以得到

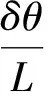
(14)

因此，扭转刚度的近似计算公式为

(15)

此公式假设所有层之间始终保持接触状态。

4 有限元计算法

在有限元分析软件的选择上，选用ABAQUS/Explicit来进行计算[6]。ABAQUS/Explicit求解器可很容易地分析包括多个独立物体的相互复杂接触问题，无需进行迭代就能确定非线性问题的解答，且需要的磁盘空间和内存比较小。

4.1 各层模型及网格划分

在建模阶段可借助有限元软件ANSYS，使用APDL语言将各层模型建好之后进行组装，导入ABAQUS中进行计算[7]。

骨架层示意图如图2所示；根据剖面图建模，如图3所示。

图2 骨架层互锁截面型式Fig.2 Geometrical profile of carcass

图3 骨架层有限元模型Fig.3 Finite element model of the carcass

抗压铠装层横剖面示意图如图4所示；根据横剖面建模，如图5所示。

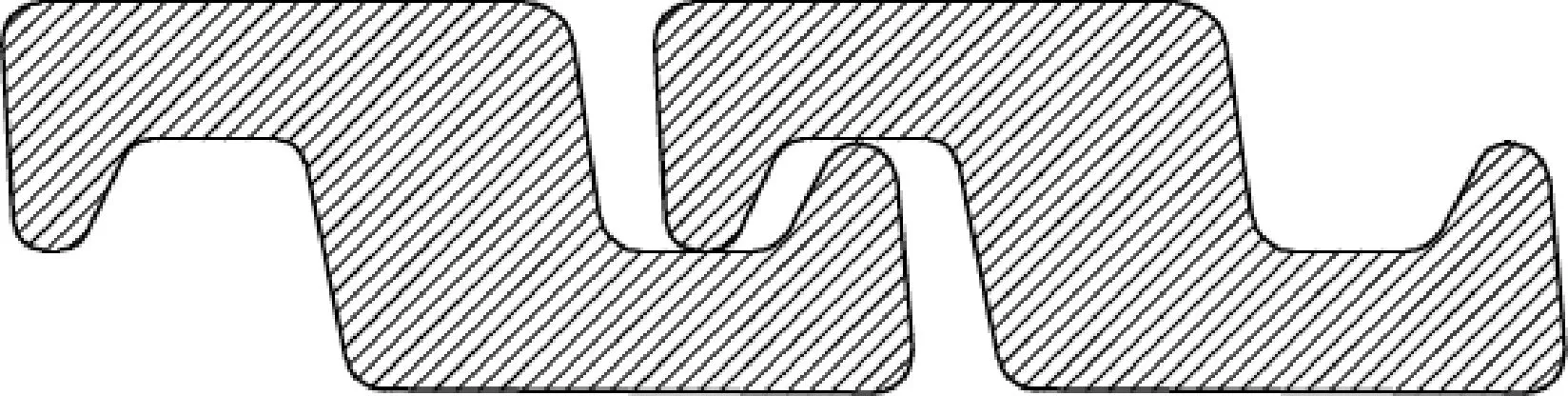
图4 抗压铠装层截面型式Fig.4 Geometrical profile of the pressure armor layer

图5 抗压铠装层有限元模型Fig.5 Finite element model of the pressure armor layer

模型建成后，总体结构的剖面图如图6所示。

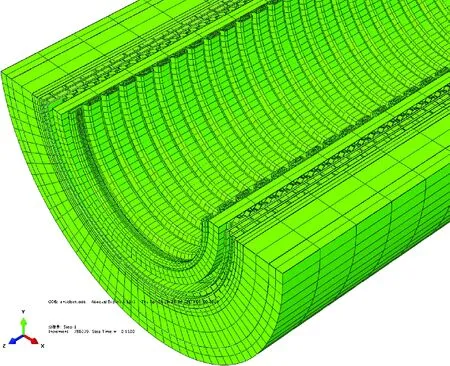
图6 有限元整体模型剖面图Fig.6 Cross-section profile of the finite element model

由于包含接触问题，模型采用三维六面体8节点非协调单元C3D8I，以获得更好的应力解和避免沙漏问题[8]。

4.2 边界条件及载荷施加

在立管两端中心建立2个几何参考点[9]，然后将两端所有节点与中心参考点之间建立运动耦合约束。立管两端的边界条件均施加在立管两端的参考点上，所有载荷也都只施加在立管顶部的参考点上。摩擦系数取0.1[10]。

立管顶部所施加的载荷分为拉伸载荷及扭矩，其中扭矩根据作用方向分两种情况进行研究。

5 计算结果对比与分析

5.1 抗拉刚度计算结果

5.1.1理论计算结果

表2为根据前文公式计算所得聚合物层的抗拉刚度。

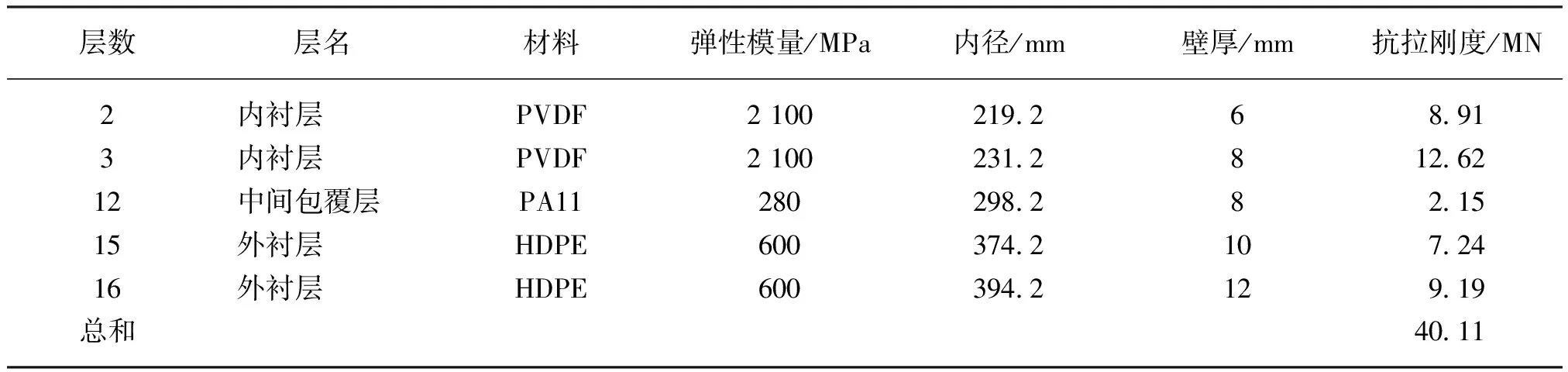
表2 聚合物层的抗拉刚度Table 2 Axial stiffness of the polymer layers

耐磨层为螺旋缠绕的塑带层，厚度很小，在刚度计算过程中不予考虑。柔性立管中的金属螺旋层包含1层抗压铠装层和2层抗拉铠装层，其中抗压铠装层螺旋缠绕角度接近90°，在轴向可自由移动，因此抗压铠装层对抗拉刚度贡献不明显，主要由抗拉铠装层抵抗轴向载荷。根据公式计算得到抗拉铠装层的抗拉刚度，如表3所示。

表3 抗拉铠装层的抗拉刚度Table 3 Axial stiffness of the tensile layers

从表3可以看出，抗拉铠装层的抗拉刚度为659.62MN；而由表2可知，聚合物层的抗拉刚度值为40.11MN，大约只占抗拉铠装层刚度值的6%。

5.1.2有限元计算结果

在轴向载荷作用下，模型整体应力云图如图7所示。

图7 轴向载荷作用下整体模型应力云图Fig.7 Axial stress contour

从图7可以看出，在轴向载荷作用下，内外抗拉铠装层的应力相对其他各层都要大。

通过有限元分析，可以得到轴向载荷与轴向应变之间的关系如图8所示。

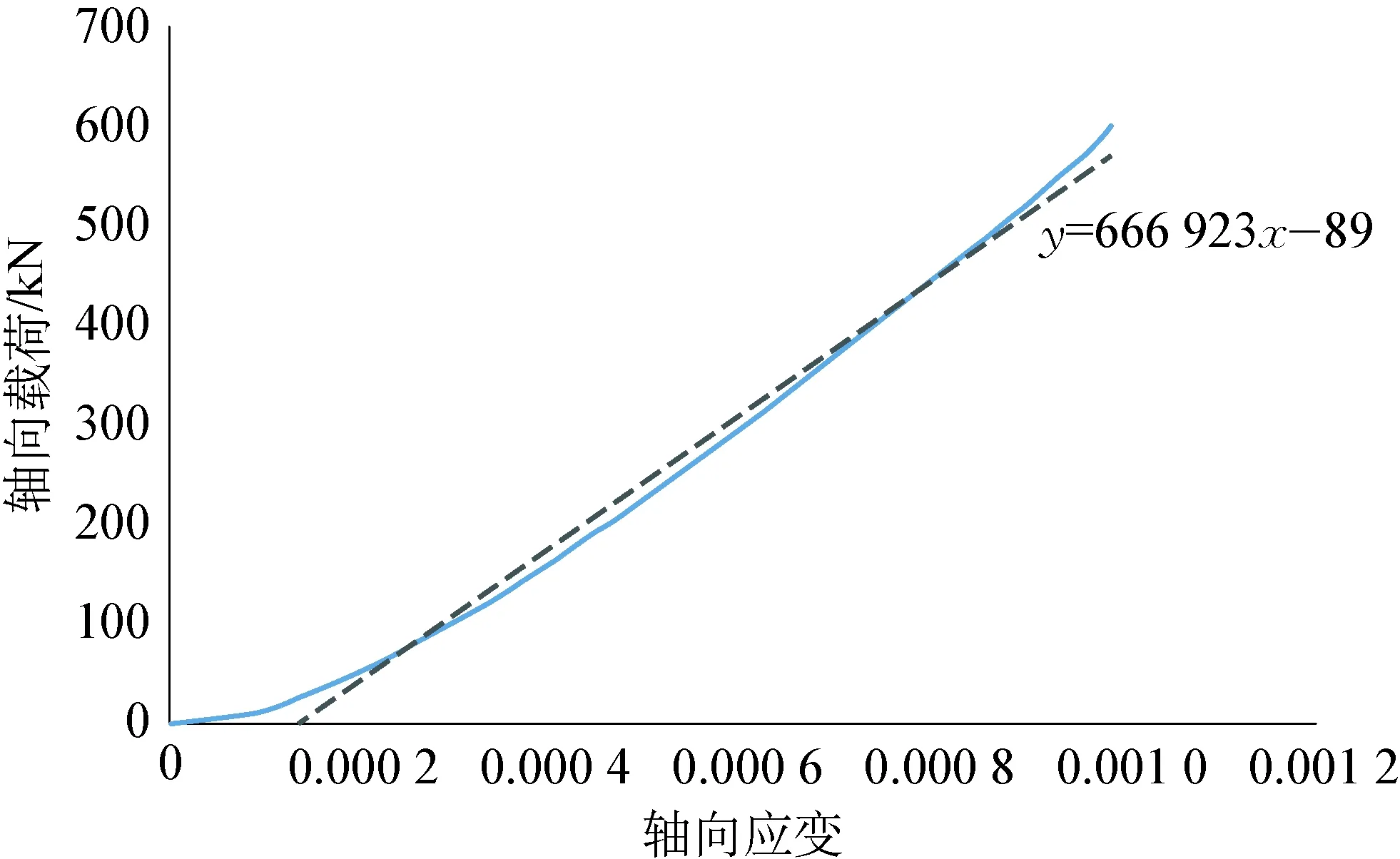
图8 轴向载荷-应变关系Fig.8 Axial force and axial strain relationship

图8中实线代表立管在轴向载荷作用下的应变变化，虚线为趋势拟合线，其斜率代表有限元计算得到的立管轴向抗拉刚度。

根据有限元计算结果可得，立管抗拉刚度值为666.92MN。

5.1.3结果对比

表4为有限元分析结果与公式计算结果的对比情况。

表4 抗拉刚度计算结果对比

从表4可以看出，两者计算结果相近，误差为1%，证明有限元计算结果和理论计算结果均正确。

同时可以看出，立管在轴向载荷作用下，抗拉铠装层是影响立管轴向抗拉能力的重要层。

5.2 抗扭刚度计算结果

5.2.1理论计算结果

对聚合物层的抗扭刚度进行计算，结果如表5所示。

表5 聚合物层的抗扭刚度Table 5 Torsional stiffness of the polymer layers

在柔性立管三层金属层中包含一层抗压铠装层和两层抗拉铠装层。由于抗压铠装层缠绕角度接近90°，抗压铠装钢线在环向可以自由转动，因此在计算抗扭刚度时不考虑其影响，故而柔性立管的抗扭能力主要由抗拉铠装层体现。抗扭刚度计算公式前文已经给出，最终计算得出抗拉铠装层的抗扭刚度如表6所示。

表6 抗拉铠装层的抗扭刚度Table 6 Torsional stiffness of the tensile layers

从以上结果可以看出，抗拉铠装层的扭转刚度值为7 399.63kN·m2，聚合物层的抗扭刚度值为362.0kN·m2，大约只占抗拉铠装层扭转刚度的5%。因此，柔性立管在扭矩作用下，抗拉铠装层承受主要扭矩载荷。

5.2.2有限元计算结果

抗拉铠装层的轴向缠绕角度为35°。沿Z轴扭矩采用线性增加和线性卸载的方式施加在立管自由端的参考点上，方向分别为顺时针和逆时针，大小相同。

在扭矩作用下，模型整体应力云图如图9所示。

从图9可以看出，在扭矩作用下，内外抗拉铠装层应力较其他各层更大，说明主要由抗拉铠装层承受扭矩作用。

根据有限元计算，得到扭矩与扭转曲率之间的关系图，如图10所示。

图10中曲线斜率代表抗扭刚度，顺时针抗扭刚度值为8032kN·m2，逆时针抗扭刚度值为10347kN·m2。逆时针刚度比顺时针刚度大，主要

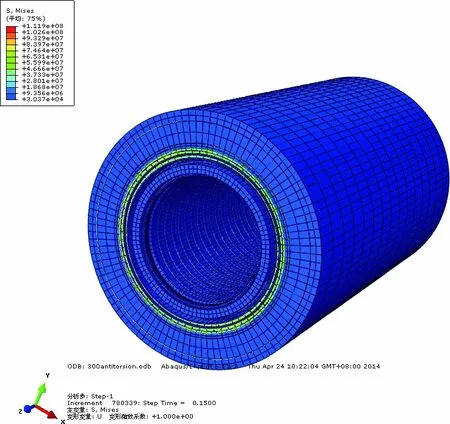
(a) 逆时针扭矩

(b) 顺时针扭矩图9 扭矩作用下模型整体应力云图Fig.9 Torsional stress contour

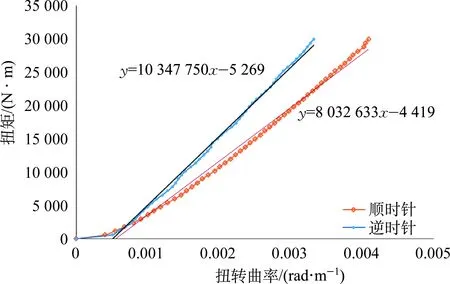
图10 扭矩与扭转曲率之间的变化关系Fig.10 Relationship between torque and twisting curvature

是因为逆时针扭矩方向与外抗拉铠装层旋转方向相同，而外抗拉铠装层的半径要比内抗拉铠装层大。

5.2.3结果对比

将有限元分析结果与公式计算结果进行对比，如表7所示。

表7 不同方法得到的抗扭刚度值

从表7可以看出，三者在数量级上一致，相比较而言理论公式计算值更为保守，而有限元计算结果偏大，且不同方向的抗扭刚度不同，逆时针抗扭刚度值较大，主要是由于此时扭矩方向与外抗拉铠装层旋转方向相同，也说明扭矩作用方向对扭转刚度的计算影响比较大，在今后的研究中应注意扭矩的作用方向与抗拉铠装层中螺旋钢线的旋转方向之间的关系。

6 结 语

根据理论计算公式和ABAQUS软件有限元分析，针对300m水深8英寸输油软管，分别对柔性立管抗拉和抗扭刚度进行计算并对比，最终得出以下结论：

(1) 通过理论公式计算结果与有限元计算结果的对比，可以看出柔性立管在轴向载荷和扭矩作用下，理论计算结果与有限元结算结果较为一致，在抗扭刚度计算中，理论计算结果相对有限元计算结果更偏保守，在今后的柔性立管设计过程中两种方法均可使用。

(2) 由于理论计算法简便快速，可以在前期设计阶段使用，以便节省时间；有限元计算法可以在详细设计阶段用于校核刚度计算结果，但最终仍需要通过试验进行验证。

(3) 柔性立管抗拉刚度和抗扭刚度主要由抗拉铠装层贡献，聚合物层影响不大。抗拉铠装层的宽度、厚度和缠绕角度是主要影响参数。

[1] Brack M, Troina L M B, Sousa J R M D. Flexible riser resistance against combined axial compression, bending, and torsion in ultra-deep water depths [C]. OMAE, 2005： 67404.

[2] Kagoura T, Ishii K I, Abe S, et al. Development of a flexible pipe for pipe-in-pipe technology [J]. Furukawa Review, 2003(24)： 69.

[3] Berge S, Engseth A, Fylling I, et al. Handbook on design and operation of flexible pipes [M]. Trondheim： SINTEF, 1992.

[4] 陈耕.海洋非粘结柔性管线的横截面力学性能分析[D].哈尔滨： 哈尔滨工程大学,2010.

Chen Geng. Analysis on cross-section mechanical properties of non-bonded offshore flexible pipe [D]. Harbin： Harbin Engineering University, 2010.

[5] 栾林昌.非粘合柔性立管力学性能研究[D].大连： 大连理工大学,2011.

Luan Lin-chang. Research of mechanical behavior of unbonded flexible risers [D]. Dalian： Dalian University of Technology, 2011.

[6] Perdrizet T, Leroy J-M, Barbin N, et al. Stresses in armour layers of flexible pipes： comparison of ABAQUS models [C].

SIMULIA Customer Conference, 2011.

[7] 王新敏.ANSYS工程结构数值分析[M].北京： 人民交通出版社,2007.

Wang Xin-min. Numerical analysis of engineering structure with ANSYS [M]. Beijing： China Communications Press, 2007.

[8] 庄茁,张帆,岑松,等.ABAQUS非线性有限元分析实例[M].北京： 科学出版社,2005.

Zhuang Zhuo, Zhang Fan, Cen Song, et al. ABAQUS nonlinear finite element analysis cases [M]. Beijing： Science Press, 2005.

[9] 石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京： 机械工业出版社,2006.

Shi Yi-ping, Zhou Yu-rong. Detailed notes to ABAQUS finite element analysis examples [M]. Beijing： China Machine Press, 2006.

ComparativeAnalysisofCalculationMethodsforAxialandTorsionalStiffnessofUnbondedFlexibleRiser

PEI Xiao-mei, ZHANG En-yong, LI Li-wei, ZHOU Wei-wei, CAO Jing

(CNOOCResearchInstitute,Beijing100028,China)

We present the study of unbonded flexible pipe and provide a case of 8 inch unbonded flexible riser at the water depth of 300m. Firstly, the theoretical calculation formulae are introduced for the analysis of axial and torsional stiffness of the unbonded flexible riser. On the basis of the theoretical calculation, finite element analysis is carried out by modelling all layers separately to reflect the mechanical behavior of each layer. The numerical results are compared with the theoretical results for tensile load and torsion. The different contributions of each layer are discussed. Under the axial load or torque, the theoretical results are consistent with the numerical results, and the theoretical results of torsional stiffness are more conservative. During the actual engineering design, the appropriate calculation method can be chosen according to the design stage.

unbonded flexible riser; axial stiffness; torsional stiffness; contact

2017-06-15

国家科技重大专项(2016ZX05028-005)；京直地区第四届青年科技与管理创新研究课题(JZTW2017KJ26)

裴晓梅(1988—)，女，硕士，工程师，主要从事海底管道和立管结构方面的研究。

TE973.1

A

2095-7297(2017)05-0307-08