基于频谱分析法的超声波流量计流道结构优化

耿 介，李 冬，彭 玮，杜广生



基于频谱分析法的超声波流量计流道结构优化

耿 介，李 冬，彭 玮，杜广生※

（山东大学能源与动力工程学院，济南 250061）

大尺度漩涡对超声波流量计测量误差有直接影响，该文通过频谱分析法定量研究了63 mm超声波传播路径上各点的湍流脉动频率和特征长度，得到了大尺度漩涡的分布规律，明确了大尺度旋涡比较集中地出现在超声波流量计声波传播路径的中后部的现状，为超声波流量计的流道结构优化提供了重要依据。提出用“井”字形网栅限制声道中后部漩涡尺度的优化方案。研究了3种网栅布置方案（方案1：设置单层网栅于63 mm声波传播路径中后部；方案2：设置3层均布网栅分别位于声波路径4等分点处；方案3：以10 mm间距设置3层均布网栅于声波传播路径中后部）对大尺度旋涡的抑制效果。结果表明方案3效果最好，在=50 000条件下，湍流误差仅为0.18%，且压力损失较小。因此，该优化设计有良好的工农业应用前景。

超声波；流量计；结构优化；LES；湍流；频谱分析；压力损失

0 引 言

由于超声波流量计测量范围宽，计量精度高，具备良好的高温适应性，在农业灌溉，水力输送，工业生产等领域应用广泛[1-5]。2011年，超声波流量计国际市场份额达6亿3 200万美元，并预计在2011－2016年的年增长率高达9.6%[6]。超声波流量计采集声波传播路径上的线平均速度，通过系数（即线面速度比）将线平均速度转化成面平均速度，进而获得流量[7]。由于超声波流量计仅对超声波传播路径上的线平均速度采样，故无法全面反映声道各截面上流动情况，因而易受到大尺度漩涡的影响。湍流由不同的尺度涡构成，其能量主要包含在大尺度涡中，但是大尺度的随机涡难以在有限空间和时间尺度内通过平均化处理消除，会对流动测量的稳定性产生影响。当超声波流量计的管径小于50 mm，通常采用U型反射方式延长声程以保证测量精度。U型反射超声波流量计的反射装置使得过流截面发生变化，从而造成被测流体流动特性复杂化，产生不同尺度的湍流漩涡，影响超声波流量计的测量精度和稳定性。

超声波流量计根据稳态流动设计，相关研究多基于稳态流动[6-8]。Westerweel等[9]利用SPIV技术对湍流充分段进行试验研究，重构圆管内速度剖面，对超声波流量计系数的标定提供了试验数据基础。Iooss等[10]分析了管型，壁面粗糙度，温度等因素对超声波流量计测量精度的影响。Yeh和Mattingly[11-12]利用试验研究了直角接头，双直角接头，T型接头等对超声波流量计的影响。Zheng等[13]通过数值模拟研究了由超声波换能器安装引起的突出或者凹陷对超声波流量计测量的影响。Kumar等[14]讨论了超声波在非水平安装时的平均速度剖面和修正方法。刘永辉等[15]采用数值模拟比较了不同反射装置对系数稳定性的影响。以往的文献中，通常对流动采用时均化处理，无法反应超声波流量计内非定常漩涡的发展变化。因此，该文采用瞬态数值模拟，从统计学角度研究湍流脉动，分析并优化大尺度涡对超声波流量计测量精度的影响。

在管流的中心区域，湍流能量和尺度按照对数分布。能级理论由Richardson[16]提出，Kolmogorov等[17-18]发展和量化了对数斜率，并提出了湍流最小尺度的概念。邱翔等[19]对湍流的相干结构进行了综述研究，认为湍流信号的研究有必要进行湍流空间尺度分解。因此，本文以单声道U型超声波流量计为研究对象，首次引入能级理论和频谱分析法讨论超声波传播声道上的湍流脉动。从减少大尺度脉动的角度，提出超声波流量计流道结构优化方案。

1 数值模拟计算

大尺度旋涡为各向异性的湍流脉动，雷诺时均法（reynolds average Navier-Stokes，RANS）对湍流脉动作了时均化处理，无法再现各个尺度涡脉动能量的统计学规律。Martins等[20]提出漩涡研究推荐使用大涡模拟（large eddy simulation，LES）。与直接数值模拟（direct numerical simulation，DNS）相比，LES没有求解小尺度运动，节省了计算资源。当LES的亚格子尺度位于各向同性区时，对大尺度涡的求解范围覆盖流动各向异性区，可以充分展现由反射装置引入的不同尺度漩涡。故本文通过LES获取流场信息。

1.1 亚格子模型

LES无法直接求解Navier-Stokes方程[21]，Navier-Stokes方程中亚格子应力项τ需要通过亚格子模型计算。该应力包括未求解尺度和求解尺度间的相互作用，以及求解尺度和未求解尺度内部的相互作用[22]。使用动态一方程亚格子模型来模拟小尺度运动，亚格子应力项求解方程如下：

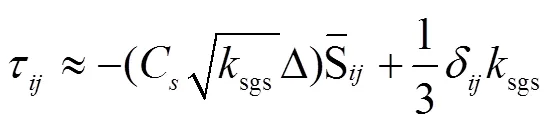
动态一方程亚格子模型根据亚格子湍动能sgs和亚格子过滤尺寸决定系数C，进而决定亚格子应力，通过求解sgs使控制方程封闭，其具体求解公式详见参考文献[23]。与常用的Smagorinsky模型相比较，由于使用了亚格子湍动能sgs，动态一方程亚格子模型对剪切流动模拟更准确[22]。由于研究课题为内流问题，流体受反射装置影响产生剪切运动，故选择动态一方程亚格子模型。

1.2 网格设置和边界条件

数值模拟通过开源CFD软件Openfoam进行。入口边界设置为inletOutlet即平均速度入口，入口压力为zeroGradient。出口条件设置为压力定值出口，fixedValue，出口速度设置为inletOutlet，沿出口外法线方向速度梯度设置为0，负向回流速度设置为0。另外，对速度场，压力场和湍动能场的计算残差要求均为10-5。时间分辨率为5×10-5s，计算周期为稳定后的1 000个时间步长。耦合计算基于PIMPLE算法，该方法稳定性高，计算速度快。

本文中体网格区域的特征长度取5×10-4m，该尺度的湍流脉动是各向同性的，符合Kolmogorov[17,24]提出的对数斜率。由于各向异性区的湍流尺度大于各向同性区[21]，而本文研究尺度集中在各向异性区，因此LES求解尺度足够小，可以充分反映超声波流量计内不同尺度漩涡。同时，内流问题中边界层的求解精度十分重要，故采用了近壁面直接数值求解的方式。根据Ansys CFX-Solver Theory Guide[25]，边界层网格的分辨率要求低于+=5即黏性底层厚度，故底层边界层网格特征长度设置为4×10-5m。

1.3 物理模型及数值模拟验证

图1a为U型反射超声波流量计物理模型。虚线表示超声波传播声道，位于两反射柱间的管道中心，长度为63 mm，在该段超声波信号受轴向流动影响加减速，是时差产生的主要区域，取上游反射柱的反射面中心点为坐标原点（0, 0, 0），则下游反射柱的反射面中心点为（63 mm, 0, 0）。在数值模拟中，超声波流量计基表前设置10倍管径，即200 mm以消除平均速度入口造成的入口段问题；在超声波流量计基表后设置15倍管径，即300 mm以降低出口约束对内部流动造成的影响。

图1b为LES模拟与文献[26]中的粒子图像测速（particle image velocimetry，PIV）试验的对比验证。选取超声波流量计重要仪表参数系数作为对比项。系数定义为=U/U，即传播声道上线平均流速U与管道截面平均流速U的比值。=2 300时，系数高达1.91，=5 000，10 000，15 000，20 000时，系数在1.3附近波动。LES的系数模拟结果与PIV试验数据基本吻合，最大相对误差位于=10 000处，为1.26%。LES模拟与PIV试验结果的相对误差低于5%[27]，说明本文所采用的LES模拟方法及各项参数设置是正确的。

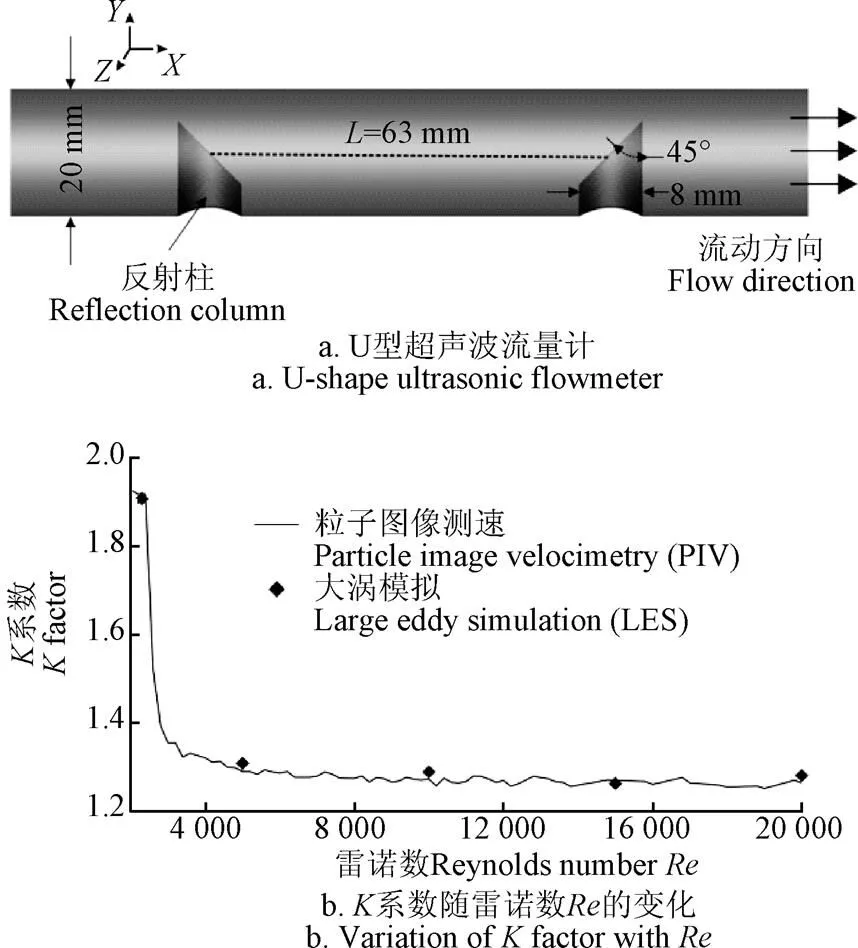
图1 物理模型和数值模拟验证

1.4 湍流统计方法

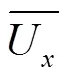
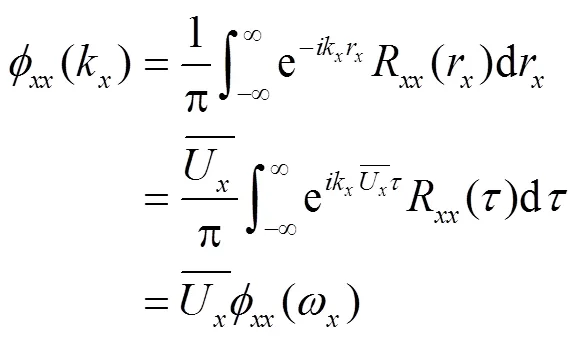
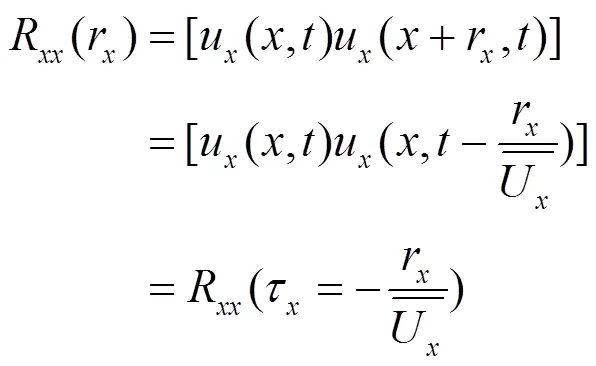
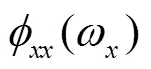
2 U型反射超声波流量计的流场特征

如图2a所示，由于上游反射柱的扰动，流动在上游反射柱后产生大尺度漩涡，=5 000时，大尺度漩涡以驻涡形式展现，=50 000时，旋涡脱落明显。由此可以判断，雷诺数较大时，湍流误差影响变大。另外由于流速的增大，时差变大，电学误差和机械误差对时差的影响降低，湍流误差对超声波流量计的测量的产生更大比例的影响。

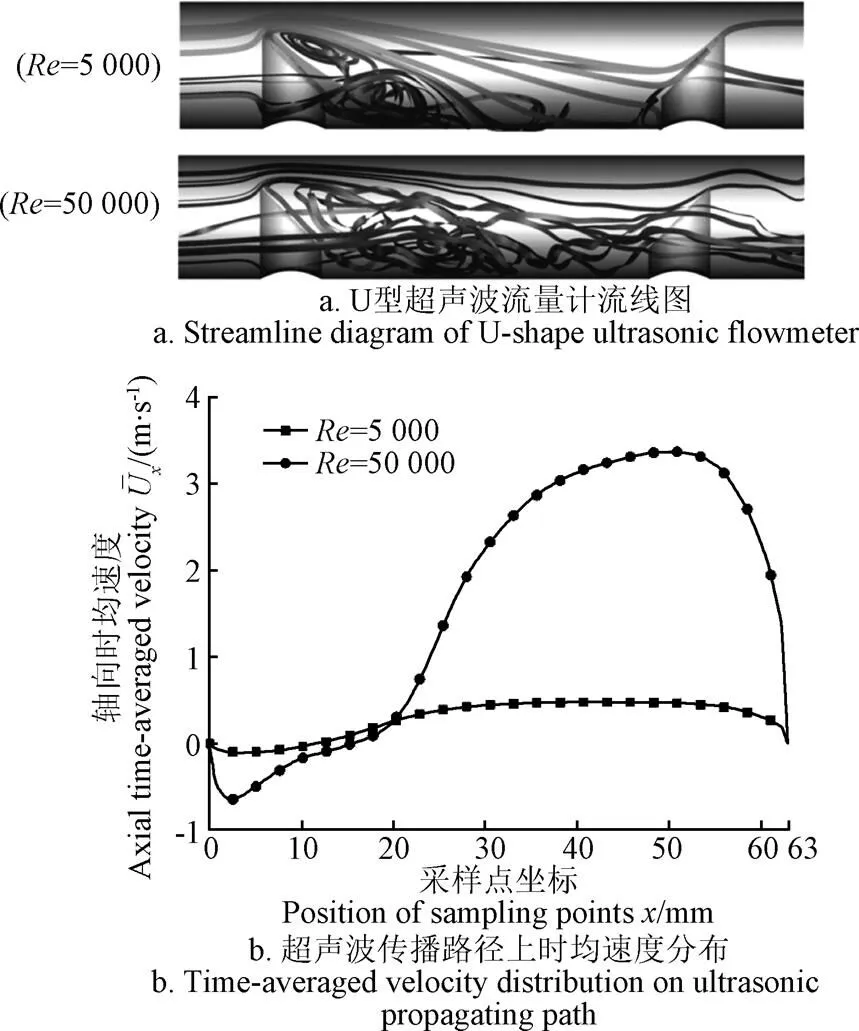
图2 反射装置对流场的影响

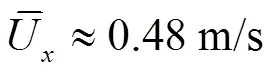
如图3c所示，=5 mm处的频谱曲线在F=315 Hz处产生了峰值，为反射柱引入的湍流脉动频率。随着湍流的发展，在=25 mm处，湍流脉动向大尺度发展，315 Hz处的峰值不再明显，在100~315 Hz区间内形成了Kolmogorov对数斜率−5/3，在100 Hz处产生拐点。根据Kolmogorov相关理论[17,24]，−5/3的对数斜率区对应在该尺度范围内湍流充分发展，上拐点表明湍流向大尺度传播受阻。由图2c知，25 mm处平均速度约为1.07 m/s，根据公式（3）、（4），上拐点对应的特征长度约等于10 mm，为圆管管径尺度的一半，故可推断100 Hz处拐点表示湍流脉动的发展受到管径限制。在=50 mm处，−5/3斜率区间的上拐点和下拐点均向高频移动，上拐点约为300 Hz，下拐点为980 Hz左右。由图2c可知，50 mm处的平均速度约为3.4 m/s，根据公式（3）、（4），上拐点特征长度约为10 mm，与25 mm曲线所表征特征长度相同，频率增量与速度增量呈正比；=25 mm和=50 mm处湍动能大于=5 mm处的湍动能，故超声波基表中后段为湍流误差产生的主要区域，在该区域大尺度涡发展至管径尺度的一半。

在超声波基表中后段的高速区，湍流脉动最大尺度到达管径尺度的一半，并受到管径尺寸限制，不再随平均流速增加。若引入小尺度结构打破大尺度漩涡，可以控制湍流脉动最大尺度。大尺度涡的减少有利于超声波流量计通过声波路径上的线平均消除湍流脉动的影响，提高超声波流量计测量稳定性。因此，下文通过流道结构优化抑制超声波传播声道中后部的大尺度漩涡。

图3 超声波流量计传播声道上的湍流脉动

Fig.3 Turbulent fluctuation on ultrasonic reflecting path

3 流道结构优化

3.1 网栅设计及分布方案

商用U型超声波流量计多采用过流通道缩颈增大平均流速，如图4a所示。缩颈设计提高测量的信噪比，但是增大了压力损失[29]。为了降低压力损失并保持测量精确性，可采用“井”形网栅限制湍流脉动尺度，来代替缩颈结构，该种设计源于低速风洞中的蜂窝器原理[30]，网栅结构如图4b所示。网栅中心为正方形，边长4 mm，该结构可以打碎大尺度漩涡，同时又不影响声波信号的传播。栅条为0.5 mm直径圆柱，这种结构可以最大限度地减少网栅本身带来的压力损失。

据图3c频谱分析结论，为了抑制超声波传播声道中后部的大尺度漩涡，本文设计了3种不同的网栅分布方案。方案1设置单层网栅于63mm声波传播路径中后部=38 mm处; 方案2设置3层均布网栅分别位于声波路径4等分点=31.5 mm，=41.5 mm，=51.5 mm处; 方案3以10mm间距设置3层均布网栅于声波传播路径中后部=31.5 mm，=41.5 mm，=51.5 mm处，如图4c所示。通过3种不同网栅分布方案的对比研究，可以得到不同网栅数量和不同网栅位置，对超声波湍流脉动误差和压力损失带来的影响，并得到最佳网栅分布。

图4 U型超声波流量计流道结构优化

3.2 优化方案的对比研究

超声波流量计的测量误差受传感器的延时、算法的系统误差和流动误差综合影响。在本文中仅讨论由于流动引发的湍流脉动误差，定义湍流误差为3/U，U是超声波传播声道上线平均速度，是传播声道上瞬态线平均速度的标准差。根据正态分布，U±3可以概括99.7%的数据样本。

表1比较了6种不同的U型超声波流量计4个关键设计参数（线平均速度U，速度标准差，湍流误差，压力损失∆）。其中YFCH-20是一种准确度等级2级[31]商用超声波流量计，在表内采用缩颈设计，测量误差限为±2%。YFCH-20的测量误差包括所有的系统误差，例如电子误差、机械误差、流动误差。YFCH-20的压力损失由产品手册中的压损曲线获得。

表1 6种U型超声波流量计的比较

当=5 000，所有超声波流量计湍流误差均在0.1%以内。由此可知。低流量时湍流脉动对超声波流量计测量影响较小。对于压力损失，方案1～3和基础U型超声波流量计的压力损失仅为0.1 kPa左右。缩颈型超声波流量计和YFCH-20的压力损失分别为0.29和0.31 kPa。说明在低流量时，网栅引入的压力损失较小，方案3较缩颈设计压损下降55%。方案2的网栅设置降低了超声波传播声道上的平均速度，导致相对较大的湍流误差。

当=50 000，管道内流速的增加导致了更大的湍流误差，其中基础U型超声波流量计的误差高达2.92%，湍流脉动对超声波测量产生明显影响。方案3的湍流误差与缩颈设计的湍流误差较小，分别为0.18%和0.17%。高流量时，方案1～方案3的压力损失仍远远小于缩颈型超声波流量计及YFCH-20，方案3较缩颈设计压损下降下降61%。由于方案1仅引入单个网栅，对湍流脉动的抑制不足，在高流量时线速度标准差较大，湍流误差为0.72%。

综合而言，随着流量的增加，湍流误差对超声波流量计测量的影响变大。与方案1～方案2相比，方案3的湍流误差在不同雷诺数下的湍流误差较小，接近缩颈型超声波流量计。并且方案3压力损失较小，与缩颈型超声波流量计相比，压损降低55%以上，具有替代缩颈设计的潜力。

3.3 方案3的流场探究

据表1速度标准差可知，大流量=50 000时超声波流量计速度脉动远大于=5 000时的速度脉动，故以=50 000为例探究方案3设计优越性。网栅的引入会影响截面上速度的分布，进而影响测量中心线上的轴向速度，如5a瞬态速度云图所示，由于大尺度涡受到网栅限制，超声波流量计上部高速区和下部低速区的混合程度减弱，呈分层流动。同时，网栅截面附近可以观察到小尺度漩涡的产生。图5b为超声波传播声道上的时均速度分布，在声道中部，即第一个网栅附近速度达到最大值3.11 m/s。在网栅控制的区域，=30～55 mm的区间内，轴向时均速度沿方向在2.5 m/s附近上下震荡，整体震荡幅度逐步减弱，流速相对稳定。图5a中流动分层现象和图5b中的速度稳定区可以共同说明，方案3在=30～55 mm区间内有效抑制了大尺度漩涡。

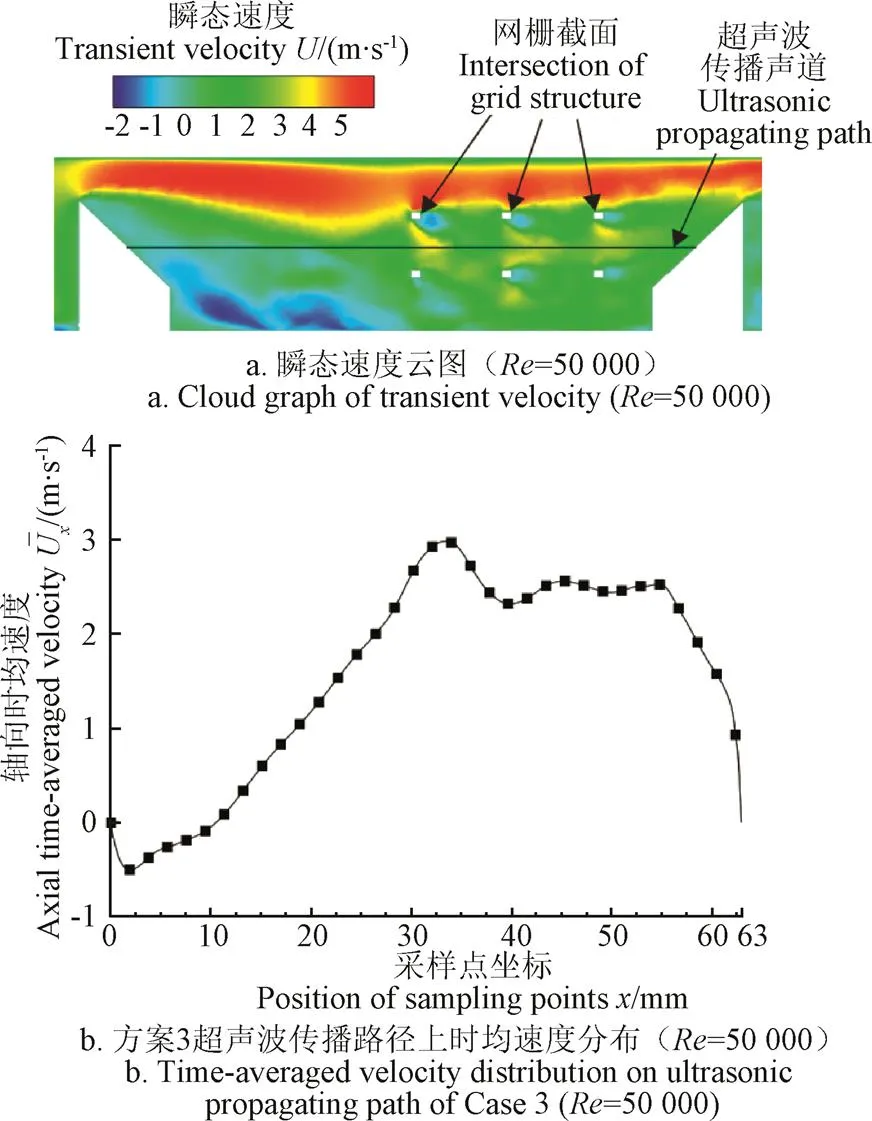
图5 设计3网栅装置对超声波流场的影响

方案3首个网栅位于传播声道中心，=31.5 mm处。为分析网栅对湍流脉动的影响，在首个网栅前后分别取采样点。前期工作中发现，≤25 mm处湍流脉动受网栅影响不明显；在=35 mm处受湍流脉动首个网栅影响，且不被第二网栅干扰，故采集=25 mm和=35 mm处的瞬态速度计算频谱曲线，如图6所示。=25 mm处的频谱曲线与图3c中=25 mm的频谱曲线结构相近，有较明显的−5/3对数斜率，在对数斜率区湍流充分发展，上拐点300 Hz受壁面限制，其尺度约为10 mm。=35 mm频谱曲线与=25 mm处频谱曲线的相比，Kolmogorov对数斜率−5/3消失，表明位于网栅后湍流脉动未充分发展。在<500 Hz区域，频谱曲线趋于水平，在=1 000 Hz附近产生峰值，可以推断，网栅结构打碎大尺度涡，限制湍流能量向低频区发展，同时破碎漩涡转化为高频湍动。由于网栅附近区域内流速相对稳定，根据公式（3）、（4），低频脉动反映为大尺度涡，高频脉动表征小尺度涡。小尺度涡对超声波流量计测量的影响小于大尺度涡，有利于超声波流量计获得稳定的线平均速度。因此网栅的具有抑制大尺度漩涡的作用，方案3可有效降低大尺度漩涡对超声波流量计测量的影响。

图6 方案3一维频谱

4 结　论

为了抑制超声波传播声道上的大尺度漩涡提高检测精度，本文以单声道U型超声波流量计为研究对象，用频谱分析法研究了超声波流量计声波传播路径上漩涡的尺度及分布情况；基于上述研究结果，提出了“井”字形网栅抑制大尺度漩涡提高检测精度的优化方案。其主要结论如下：

1）频谱分析的研究结果表明，对检测结果直接产生影响的大尺度漩涡主要分布在声波传播路径的中后段。

2）“井”字形网栅可以打碎大尺度涡，使低频脉动量减少，高频脉动量增加，有利于提高超声波流量计的测量精度。

3）布置于超声波流量计声波传播路径中后部的3层均布井字形网栅对大尺度涡的抑制作用明显，当=50 000时其湍流误差仅为0.18%，且压力损失较缩颈U型超声波流量计下降61%。

本文的研究方法及结果有显著的科学意义和重要的工程应用价值，为相关研究提供了重要参考。

[1] Luca A, Marchiano R, Chassaing J C. Numerical simulation of transit-time ultrasonic flowmeters by a direct approach[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2016, 63(6): 886－897.

[2] Saldanha W E, Bortoni E D C. Development and signal processing of ultrasonic flowmeters based on transit time[C]//IEEE International Conference on Industry Applications, 2017: 1－7.

[3] 刘永辉. 圆管过渡区流速特性的研究[D]. 济南：山东大学，2011.

Liu Yonghui. Research of Characteristics of Transition Flow in Pipes[D]. Jinan: Shandong University, 2011. (in Chinese with English abstract)

[4] Kurniadi D. Transit time multipath ultrasonic flowmeter: An issue on acoustic path arrangement[J]. Applied Mechanics & Materials, 2015, 771: 3－8.

[5] Carlander C. Installation Effects and Self Diagnostics for Ultrasonic Flow Measurement[D]. Luleå: Luleå Tekniska Universitet, 2001.

[6] Processing. The World Market for Ultrasonic Flowmeters [N/OL]. Processing, 2014[2014-06-06]. https://www. processingmagazine.com/ultrasonic-flowmeter-market-exceeds-600-million-worldwide-studies-find/.

[7] Rajita G, Mandal N. Review on transit time ultrasonic flowmeter[C]//International Conference on Control, Instrumentation, Energy & Communication, IEEE, 2016: 88－92.

[8] Borodičas P, Ragauskas A, Petkus V, et al. Innovative method of flow profile formation for ultrasonic flowmeters[J]. Elektronika Ir Elektrotechnika, 2015(10): 91－94.

[9] Westerweel J, Draad A A, Hoeven J G T V D, et al. Measurement of fully-developed turbulent pipe flow with digital particle image velocimetry[J]. Experiments in Fluids, 1996, 20(3): 165－177.

[10] Iooss B, Lhuillier C, Jeanneau H. Numerical simulation of transit-time ultrasonic flowmeters: uncertainties due to flow profile and fluid turbulence[J]. Ultrasonics, 2002, 40(9): 1009－1015.

[11] Yeh T T, Mattingly G E. Laser Doppler Velocimeter Studies of the Pipeflow by a Generic Header[M]. US Department of Commerce, Technology Administration, National Institute of Standards and Technology, 1995.

[12] Yeh T T, Mattingly G E. Comuper simulations of ultrasonic flow meter performance ideal and non-ideal pipeflows[C]// ASME Fluids Engineering Division Summer Meeting. 1997: 1－6.

[13] Zheng dandan, Zhang Pengyong, Xu Tianshi. Study of acoustic transducer protrusion and recess effects on ultrasonic flowmeter measurement by numerical simulation[J]. Flow Measurement & Instrumentation, 2011. 22(5): 488－493.

[14] Kumar K, Swain T K, Ekhande C S, et al. Effects of flow measurement on sloped pipes using ultrasonic flowmeter[C]// International Conference on Industrial Instrumentation and Control, IEEE, 2015: 1490－1494.

[15] 刘永辉，杜广生，陶莉莉，等. 反射装置对超声波流量计水流特性影响的研究[J]. 仪器仪表学报，2011，32(5)：1183－1188.

Liu Yonghui, Du Guangsheng, Tao Lili, et al. Study on the influence of ultrasonic reflection device on the flow characteristics of ultrasonic flowmeter[J]. Chinese Journal of Scientific Instrument, 2011, 32(5): 1183－1188. (in Chinese with English abstract)

[16] Richardson L F. Weather Prediction by Numerical Process[M]. Cambridge, Cambridge University Press, 2007.

[17] Kolmogorov A N. Dissipation of energy in locally isotropic turbulence[J]. Proceedings of the Royal Society of London, 1991, 434(1890): 15－17.

[18] Li Ming, Vitányi P. An Introduction to Kolmogorov complexity and its applications[J]. Texts in Computer Science, 2008, 60(3): 1017－1020.

[19] 邱翔，刘宇陆. 湍流的相干结构[J]. 自然杂志，2004，26(4)：187－193.

Qiu Xiang, Liu Yulu, Turbulent coherent structure[J]. Chinese Journal of Nature, 2004, 26(4): 187－193. (in Chinese with English abstract)

[20] Martins R S, Ramos R. Bend installation effects on the correction factor of single-path ultrasonic flow meters[C]// Proceedings of the XXXII Iberian Latin American Congress on Computational Methods in Engineering, 2011: 579-587.

[21] Pope S B. Turbulent Flows[M]. Bristol, IOP Publishing, 2001.

[22] Sagaut P. Large Eddy Simulation for Incompressible Flows: An Introduction[M]. Berlin, Springer Science & Business Media, 2006.

[23] Davidson L. Large Eddy Simulation: A dynamic one-equation subgrid model for three-dimensional recirculating flow[C]// 11th International Symposium on Turbulent Shear Flow, 1997(3): 112－116.

[24] Kolmogorov A N. The local structure of turbulence in incompressible viscous fluid for very large reynolds numbers[J]. Proceedings: Mathematical and Physical Sciences, 1991, 434(1890): 9－13.

[25] ANSYS. Ansys CFX-Solver Theory Guide [M]. Canonsburg, ANSYS Inc, 2013.

[26] Liu Zhenggang, Du Guangsheng, Shao Zhufeng, et al. Measurement of transitional flow in pipes using ultrasonic flowmeters[J]. Fluid Dynamics Research, 2014, 46(5): 055501. doi:10.1088/0169-5983/46/5/055501.

[27] 吴万荣，梁向京，娄磊. 移动式双螺杆空气压缩机系统动态特性分析[J]. 农业工程学报，2017，33(2)：73－79.

Wu Wanrong, Liang Xiangjing, Lou Lei. Dynamic characteristics analysis of portable twin screw air compressorsystem[J]. Chinese Society of Agricultural Engneering(Transactions of the CSAE), 2017, 33(2): 73－79. (in Chinese with English abstract)

[28] Favre A, Gaviglio J, Dumas R. Structure of velocity space- time correlations in a boundary layer[J]. The Physics of Fluids, 1967, 10(9): 138－145.

[29] 李冬，孙建亭，杜广生，等. 结构参数对超声波流量计水流特性影响的研究[J]. 仪器仪表学报，2016，37(4)：945－951.

Li Dong, Sun Jianting, Du Guangsheng, et al. Study on the flow characteristics of ultrasonic flowmeter with different structure parameters[J]. Chinese Journal of Scientific Instrument, 2016. 37(4): 945－951. (in Chinese with English abstract)

[30] Goto R. CFD simulation and experimental validation of a new closed circuit wind/water tunnel design[J]. Journal of Fluids Engineering, 1998, 120(2): 762－801.

[31] 中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会. 闭满管道中水流量的测量饮用冷水水表和热水水表：GB/T 778.1~3-2007 [S]. 北京：中国标准出版社，2008：5.

Optimization design of ultrasonic flowmeter flow channel based on frequency spectrum analysis

Geng Jie, Li Dong, Peng Wei, Du Guangsheng※

(250061,)

Ultrasonic flowmeter is a non-contact flow measurement method which is widely used in various regions from agricultural irrigation to food processing. The accuracy and stability of ultrasonic flowmeter can be affected by large scale vortex because the measurement basically depends on average line velocity on the ultrasonic path rather than the whole intersection scanning. For U-shape transit-time ultrasonic flowmeter, the reflection columns extend into flow area and generate vortexes. The influence on the ultrasonic measurement from different scale vortexes is known as turbulence error. By using constriction design, commercial ultrasonic flowmeters can reduce the unfavorable impact of turbulence fluctuation and then increase its signal to noise ratio (SNR). But the pressure loss caused by the necking design is correspondingly large. In order to replace the constriction and keep applicable measurement accuracy, the discussion on the sources and correction of different measurement errors of ultrasonic flowmeter is emphasized. This paper developed a numerical simulation model for ultrasonic flowmeter based on the large eddy simulation (LES) theory and also validated it. Upon the obtained LES data, the frequency spectrum analyses are firstly practiced to study the relationship between measurement accuracy and turbulent diffusion on the basic U-shape ultrasonic flowmeter without optimization. It is found that the mean flow rate at the second half of flowmeter is relatively high and the turbulent fluctuating scale is comparatively large. Breaking the large scale vortexes at the second half is probably a good way to stabilize the turbulent fluctuation. This manuscript designed three new types of U-shape ultrasonic flowmeters with grid structure, which canceled the constriction part in the U-shape ultrasonic flowmeter. The statistical characteristics of turbulent error based on 6 different U-shape ultrasonic flowmeters are compared. The best optimized design is Case 3 which can potentially replace the U-shape ultrasonic flowmeter with constriction design due to low pressure loss. It can be found that, compared to the ultrasonic flowmeter with constriction, Case 3 reduces the pressure loss by 55% and 61% under the Reynolds number of 5 000 and 50 000 respectively. The turbulent error of Case 3 under the Reynolds number of 5 000 is 0.01%, which is as small as U-shape ultrasonic flowmeter with constriction. As for large flow rate under the Reynolds number of 50 000, the turbulent errors of Case 3 and U-shape ultrasonic flowmeter with constriction are very close, which are 0.18% and 0.17%, respectively. In order to analyze the turbulence reducing effects of Case 3, the flow characteristics of Case 3 is studied. The distribution of grid structure of Case 3 has little influence on the averaged velocity in the measured path. The velocity in Case 3 is layered without good mixing, which can be regarded as the sign of less large scale fluctuation. The introduction of grid structure can restrict the low frequency pulsation, while increasing the high frequency components. As the high frequency components are easier to be smoothed out by time average, the ultrasonic measurement is optimized. If finer grid structure is introduced, the measurement error would decline and pressure loss would correspondingly increase with high possibility. It can potentially be customized by the engineering requirements in the future.

ultrasonics; flowmeters; structural optimization; LES; turbulence; frequency spectrum; pressure loss

10.11975/j.issn.1002-6819.2017.24.014

TH814; S237

A

1002-6819(2017)-24-0104-07

2017-08-28

2017-11-13

山东省自然科学基金（编号ZR2014ZZM015）；山东省科技发展规划（2014GGX106006）

耿介，男，山东滨州人，博士生，主要从事湍流方面的研究。Email：gj_8944@163.com

杜广生，男，山东济宁人，教授，博士，主要从事流体机械方面的研究。Email：du@sdu.edu.cn

耿 介，李 冬，彭 玮，杜广生. 基于频谱分析法的超声波流量计流道结构优化[J]. 农业工程学报，2017，33(24)：104－110. doi：10.11975/j.issn.1002-6819.2017.24.014 http://www.tcsae.org

Geng Jie, Li Dong, Peng Wei, Du Guangsheng. Optimization design of ultrasonic flowmeter flow channel based on frequency spectrum analysis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(24): 104－110. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.24.014 http://www.tcsae.org