碎屑流冲击下的桥墩动力响应特征分析

毕钰璋，何思明，王东坡，孙新坡，闫帅星，周宇博，陈 政

(1.东南大学交通学院岩土工程研究所，江苏 南京 210096；2.中国科学院山地灾害与地表过程重点实验室，四川 成都 610041；3.中国科学院水利部山地灾害与环境研究所，四川 成都 610041；4.中国科学院青藏高原地球科学卓越创新中心，北京 100101；5.成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059; 6. 四川理工学院，四川 自贡 643000)

碎屑流冲击下的桥墩动力响应特征分析

毕钰璋1,2,3，何思明2,3,4，王东坡2,3,5，孙新坡6，闫帅星2,3，周宇博2,3，陈 政2,3

(1.东南大学交通学院岩土工程研究所，江苏 南京 210096；2.中国科学院山地灾害与地表过程重点实验室，四川 成都 610041；3.中国科学院水利部山地灾害与环境研究所，四川 成都 610041；4.中国科学院青藏高原地球科学卓越创新中心，北京 100101；5.成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059; 6. 四川理工学院，四川 自贡 643000)

碎屑流以其高动能和强大的破坏力被视为我国西南片区最危险的地质灾害之一，它不仅对人民群众的生命财产造成极大的危害，并且威胁到桥梁、铁路等国家的基础设施建设。本文就碎屑流冲击条件下的桥墩为研究对象，以两种不同形状的桥墩(圆柱桥墩、矩形桥墩)以及桥墩离碎屑流的物源区距离为研究条件，以离散元方法为研究手段，着重研究了碎屑流冲击桥墩时候的动力响应情况。结果表明：在相同规模以及相同距离的碎屑流条件下，圆柱形桥墩所受的瞬时冲击力的法向应力要小于矩形桥墩，切向应力则大于矩形桥墩，其所受最大冲击力以及平均冲击力都小于矩形桥墩，并且给出了物源区距离对桥墩所受冲击力的影响。研究结果对实际防灾工程有一定的指导意义。

桥墩；碎屑流；离散元；冲击力

0 引 言

碎屑流灾害是我国山区中的一种常见的灾害形式，特别是2008年汶川地震之后，西南地区次生灾害频繁，碎屑流、岩崩等灾害以其强大的破坏性成为了西南地区人民财产的主要威胁[1-3]。碎屑流灾害的发生具有很大的突然性和不确定性，当灾害发生时，几乎无法给人们留下进行警示避灾的时间；碎屑流的启动则是自然应力长期作用以及一些偶然的激发因素共同作用下的结果，固而很难给出比较准确的预测；碎屑流启动之后的运动轨迹和运动距离受到自身组成成分、碎屑流颗粒性质、坡面的岩土体性质、坡面的几何条件、植被的覆盖条件等诸多因素的综合影响而难以给予一个定论；碎屑流对结构体的冲击与单块滚石不同，不仅要考虑其多次的瞬时的冲击荷载，还要考虑堆积在结构体之上的碎屑体的静态荷载，作用机制十分复杂[4-7]。这些碎屑流灾害的特点使得碎屑流灾害机理的研究和碎屑流灾害的防治成为次生山地灾害防治的一个难点和重点。

碎屑流不仅危害人民群众的生命财产安全，而且威胁到国家的基础设施建设[1-2]。我国水电基地90%以上分布在山区。约50%道路干线穿过山区(干线公路4.24×106km，铁路104km)，受山地灾害威胁严重。特别是有些山区需要架桥通过，一旦暴发碎屑流，必将导致大量块石和漂砾冲击、撞击、剪断桥墩、桥台，并造成桥梁和桥墩断裂、垮塌和倾倒等破坏，中断车辆的通行(图1)。正是基于以上的种种考虑，这就使得彻底研究桥墩在碎屑流冲击条件下的动力响应情况显得极为必要和迫切。

图1 因碎屑流冲击桥墩而毁坏的大桥Fig.1 Motion trails of rock avalanches smashing the bridge

关于桥墩冲击破坏模式的研究，国内学者大多停留在单个滚石对其造成的冲击破坏上，而对一定规模的碎屑流冲击桥墩的研究较少[8]。也有学者尝试了多块滚石对桥墩的冲击破坏研究，但毕竟规模和数量有限，与实际的碎屑流灾害相差甚远[9]。国内外也有众多学者尝试研究了碎屑流、泥石流等和结构体之间的动力响应关系，并且取得了一定的成果和结论；然而一来研究的方式主要是采用二维数值模拟；二来研究的结构体大多是挡墙之类的支挡结构，从尺寸和形状上与桥墩有着本质上的不同[10-12]。基于此，本文着力于采用三维离散元方法，对一定规模条件下的碎屑流冲击桥墩的动力响应进行了详细的研究，并将不同桥墩形状、物源区距离等因素一并考虑在研究过程中，旨在得出一些关于碎屑流冲击桥墩条件下的规律性的结论，并对实际工程起到一定的指导作用。

1 离散元方法及参数选取

离散元方法是由Cundall和Strack在1979年创立的一种基于二维圆盘和三维圆球排列建立数值模型的方法[13]。该方法是基于颗粒间接触的位置关系以及相互作用的力学关系来求得粒子的运动状态。离散元最初被用于模拟颗粒材料，但是随着其本构模型的发展，粘结模型和平行接触模型的应用使得离散元方法能用于研究固体材料的力学特性中去。

1.1 颗粒接触本构模型

离散单元方法( discrete element method，DEM) 以圆盘体系内的二维圆盘或是颗粒体系内的三维颗粒为研究对象。宏观尺度下可以反映碎屑流的解体、运动、堆积等过程；然而在细观尺度下，具体反映为每个颗粒在不同时刻的空间变化和运动状态。通过合理的参数选取，通过颗粒体系微观条件下的非连续特性和非平衡状态，进而演化反映研究对象的整个宏观力学行为。本文研究的对象是碎屑流灾害体，重点是灾害的运动冲击过程，故而本次研究假设颗粒间处于类似于砂土工况条件下的无黏结力状态，其间使用的滑动模型是摩擦滑动模型(slip model)；颗粒间的接触模型则是线性接触模型。该法采用显式时步循环运算规则，离散元中颗粒间相互作用力主要是通过在颗粒间的接触以及牛顿第二定律来实现的。图2表示的是颗粒间的相互接触法则: 分别使用弹簧、滑块和黏滞块来分别代表颗粒间作用所产生的弹性变形、摩擦能耗、塑性变形和应变能耗。基于此，本次研究采用了三维离散元软件PFC3D来对问题进行相应的研究。

图2 颗粒间线性接触模型Fig.2 Representation of particle contact by a linear contact law

1.2 物理实验和数值实验的实验参数确定

在离散元方法中，材料的宏观运动行为取决于颗粒间接触的力学参数。然而对于参数的选取却没有一个完全有效的方式。较多的研究方式是通过物理模型和数值模型的试件压缩破坏模式相匹配，从而确定其力学参数[12]；或者是通过物理模型和数值模拟的运动堆积形态相匹配进而反演出所需参数[14-15]。本次研究在前人工作的基础上对参数进行了进一步的修正。Choi 通过数值模拟和室内试验相对比的方法确定了石英砂的参数并进行了一系列的离散元数值模拟研究[14-15]。如图3所示，Choi的数值模拟结果较好的反映了灾害体撞击结构体之后的运动路径和瞬时堆积形态，但是灾害体龙头处的形态与实验相比仍有差异。本次研究在Choi的基础上试调了参数，并使得堆积结果在大致形态上满足前人研究结果的条件下，使得灾害体的龙头处的瞬时堆积形态和实验结果相吻合(图3)。在本文的研究中，将采用通过此次反演所得的参数进行接下来的研究，尤其是碎屑流冲击作用下的桥墩动力响应研究。

图3 灾害体和结构体相互作用的各个时间步数的情况：物理实验(左列)，Choi的数值实验(中列)以及本文的数值实验(右列)Fig.3 Flow-obstacle interaction: comparison between the laboratory experiment (left) , the DEM simulation of Choi (middle) and the DEM simulation of our studies.

2 碎屑流冲击下桥墩的动力响应特征

通过图3物理实验和数值实验的对比发现：合理的参数选取可以使得数值实验从一定程度上取代物理实验并对物理实验所不好操控的条件(粒径、密实度、不同颗粒的百分比)进行进一步研究。表1显示的是通过数值模拟反演的参数，为了保证参数选取的可靠性，本次数值模拟试验中的主要参数沿用了表1中的参数。

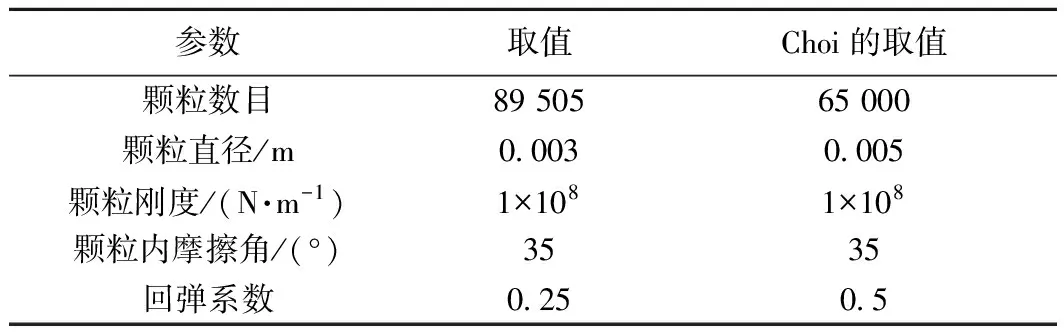
表1 数值实验中所应用的材料参数Table 1 Material parameters used in the numerical experiments

图4是本次数值模拟实验的模型，坡顶是体积为固定量V0的碎屑体，装在长a=5 m、宽b=3 m、高c=3 m的长方体容器中。斜槽长L=25 m。本次研究设置了工况的斜槽宽度S=8 m。为了排除侧限摩擦对碎屑流运动造成的能量损失，我们将滑槽两端的侧限摩擦系数设置为0。碎屑流一般在高山地区，坡面的摩擦系数势必要考虑山体植被对其的影响，Bi[16]分别对比了实验和数值模拟下的岩崩过程，并确定了PFC模拟条件下带植被的坡体摩擦系数应为1.2，因此本文在研究过程中沿用这一取值。桥墩分别采用圆柱形桥墩和方形桥墩：圆柱桥墩横截面的直径为2 m，方形桥墩截面的边长为2 m(表2)。桥墩离坡脚的距离s设为一个变量，旨在用于研究桥墩离物源区的距离对其和碎屑流之间的动力响应的影响。

图4 理想状态下边坡形状Fig.4 Geometry of the idealised slope

参数取值边坡角度α/(°)37斜槽长度/m25桥墩和坡脚距离s/m0，5，10，15，25，50桥墩高度H/m3桥墩直径(长宽)w/m2(圆柱桥墩直径)2(方形桥墩长宽)斜槽宽度/m8颗粒尺寸/m坡面摩擦系数005～0312

根据材料参数以及几何尺寸建立起来的三维离散元模型见图5。图中料箱中所装黄色颗粒集合即表示碎屑流的物源区，由于自然条件下的碎屑流颗粒体积大小不一，故而本次在相应物源区随机生成了0.05～0.3 m区间内的颗粒；并用相同的碎屑流分别冲击方形桥墩和圆柱形桥墩，并研究桥墩离坡脚不同距离条件下所受到的碎屑流动力响应情况。

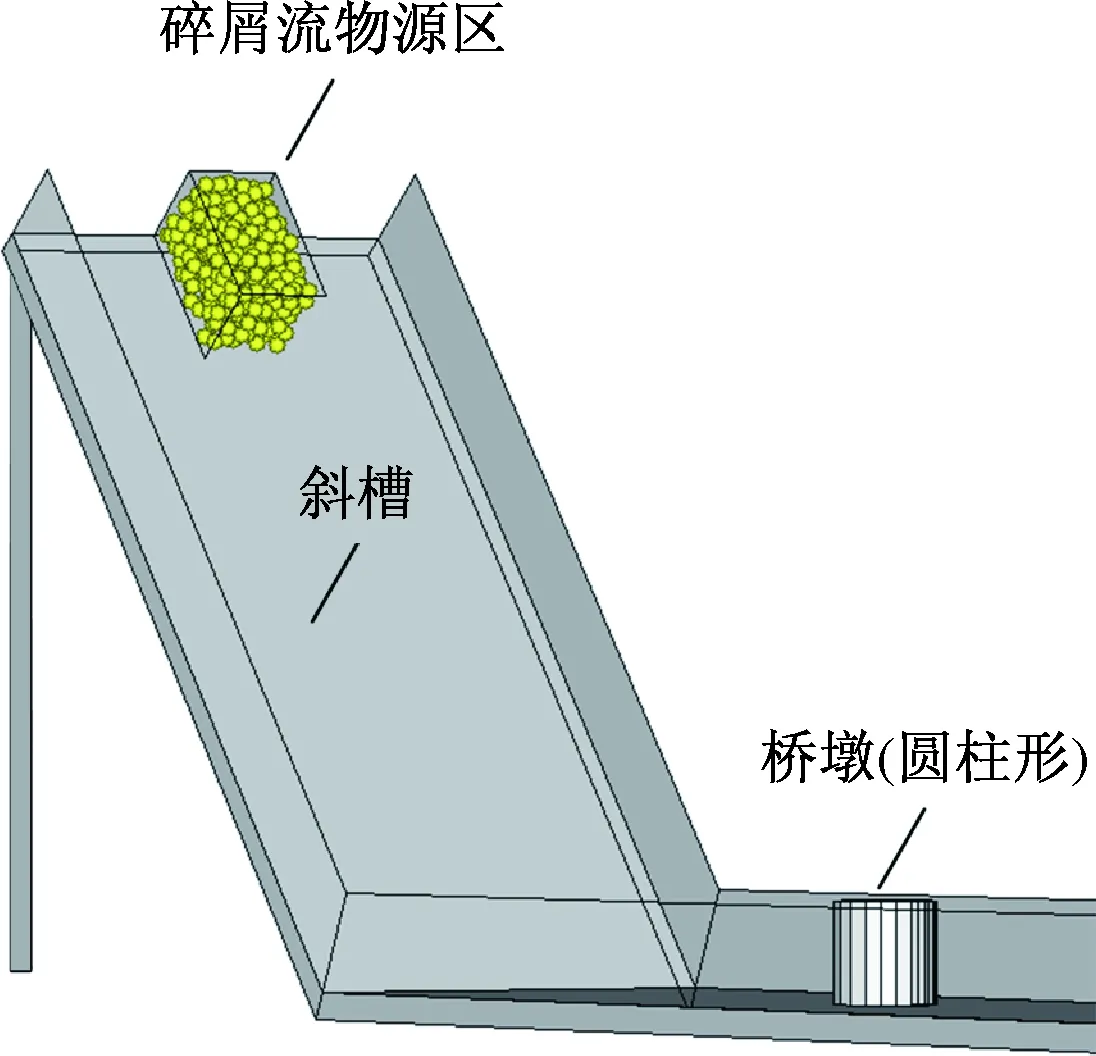
图5 根据理想边坡条件建立的三维离散元模型Fig.5 The 3D model in DEM of idealised slope

2.1 不同形状桥墩法向应力对比

碎屑流作用在桥墩上的瞬时应力不仅包括瞬时冲击力，而且还包括堆积在桥墩前缘的碎屑体产生的静力。我们沿着应力作用的方向，可以将其分解为沿着冲击方向的法向应力以及与冲击方向垂直的切向应力两个部分。图6显示了碎屑流冲击两种不同形状桥墩条件下所产生的瞬时法向应力的变化。由图6可得，圆柱桥墩所受应力是一个连续的变化曲线——几乎符合由0到波峰再到0的二次曲线分布，并在运动总时间的3/4处达到法向应力的最大值。方形桥墩的应力曲线除了应力值更大一些之外，其变化趋势和圆柱桥墩的应力曲线大体相同；但是圆柱桥墩应力曲线最后趋于0值，而方形桥墩仍然保持了一个固定值(约1.8×107N)。由此可得，在方形桥墩的前缘产生了碎屑体的堆积并产生了静压力，而碎屑流在冲击圆柱桥墩时，由于接触面的原因并未在桥墩的前缘产生碎屑体的堆积，故而静压力为零。

图6 碎屑流冲击桥墩时，作用在不同形状桥墩上的法向应力对比(s=0 m)Fig.6 Normal force of impact force exerted on bridge pier with different shape vs. time step number(s=0 m)

2.2 不同形状桥墩切向应力对比

图7显示的是碎屑流冲击不同形状桥墩下所产生的瞬时切向应力的变化。从图中可以看出，红色曲线所表示的圆柱桥墩所受到的碎屑流瞬时切向应力要远远大于方形桥墩所受的切向应力。圆柱形桥墩所受的最大切向应力甚至达到了4.2×107N，远大于方形桥墩所受的最大切向应力值(1.4×107N)，这是由于作用在不同形状桥墩的冲击力的机理不同所造成的。图8给出了碎屑流冲击力作用在不同形状桥墩上的示意图。从示意图可以看出方形桥墩的接触面为一个平面，这就使得作用在接触面上的力主要是法向冲击力为主，其受到的切向应力很小，主要是堆积在桥墩前面的堆积体摩擦所产生的沿切向的应力。

图7 碎屑流冲击桥墩时，作用在不同形状桥墩上的切向应力对比(s=0 m)Fig.7 Tangential force of impact force exerted on bridge pier with different shape vs. time step number(s=0 m)

图8 冲击力作用在不同形状桥墩时的示意图Fig.8 Avalanches impact on different type of bridge pier

2.3 不同形状桥墩冲击力对比

由于不同桥墩前缘堆积的碎屑体各不相同，故而其施加于桥墩上的静力各不相同。所以把碎屑流作用在桥墩上的冲击力单独拿来考虑显得更有说服力。图9显示的是不同桥墩所受的平均冲击力随桥墩离坡脚距离变化所产生的演化规律；图10显示的则是相同情况下的最大冲击力的演化规律。

如图9所示，图中不仅给出了不同桥墩所受冲击力的对比；而且给出了相同桥墩在离坡脚不同距离之时，碎屑流的平均冲击力的变化趋势。由图可知，方形桥墩所受的平均冲击力演化曲线始终在圆柱桥墩所受的平均冲击力演化曲线之上；该规律同时适用于桥墩所受的最大冲击力(图10)——方形桥墩上所受的最大冲击力甚至是圆柱形桥墩上的2倍，这从冲击力的角度证明了圆柱形桥墩相对于方形桥墩更适用于碎屑流发育的山谷之中。图9和图10同时显示了桥墩所受碎屑流冲击力(平均冲击力和最大冲击力)都随着桥墩离坡脚的距离增大而减小。

图9 碎屑流冲击桥墩时，作用在不同形状桥墩上的平均冲击力对比Fig.9 Average impact force exerted on bridge pier with different shape vs. time step number

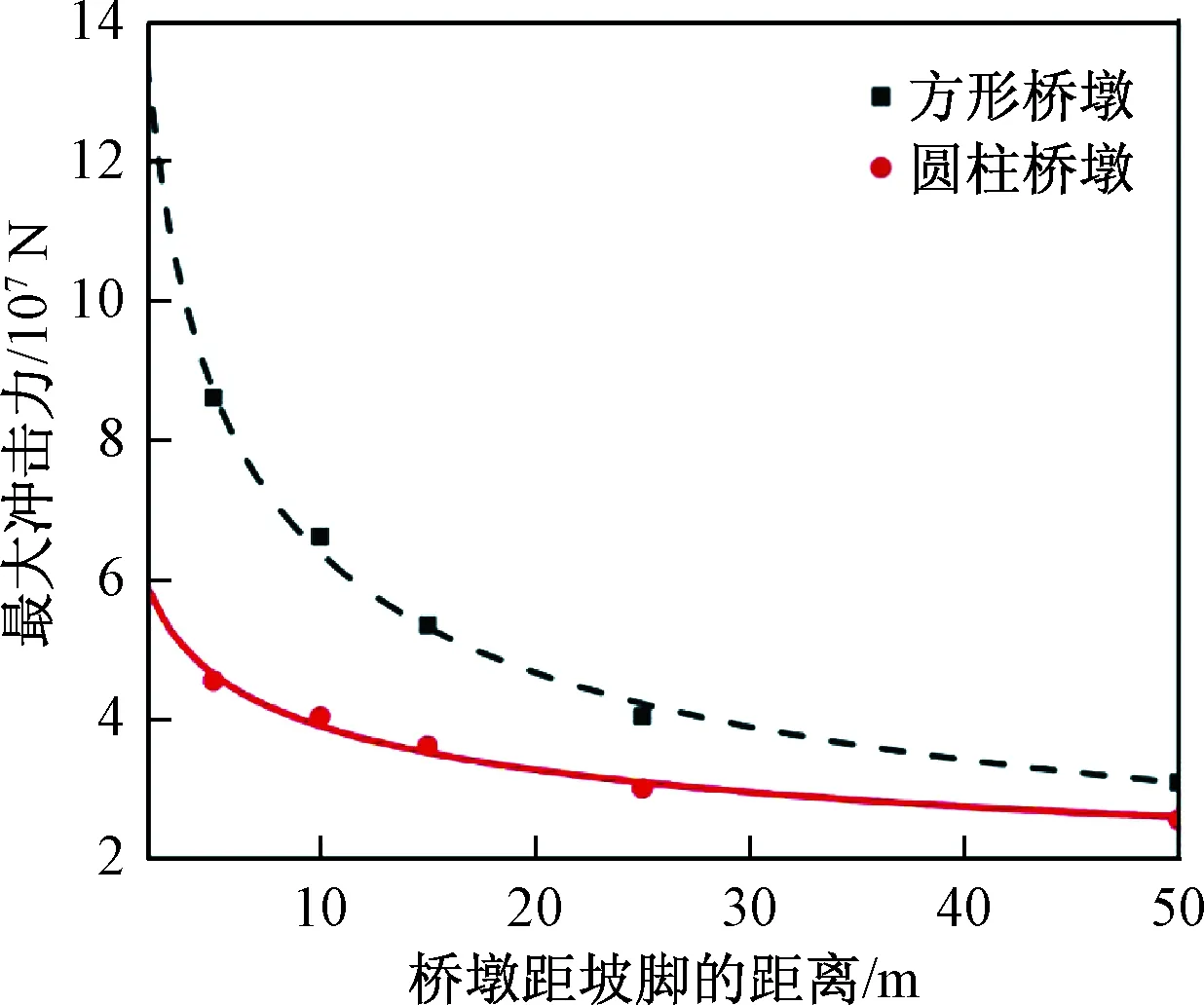
图10 碎屑流冲击桥墩时，作用在不同形状桥墩上的最大冲击力对比Fig.10 Maximum impact force exerted on bridge pier with different shape vs. time step number

3 结论

在本次研究中，我们用3D离散元实验和实际物理实验进行对比并确定了模拟参数，并构建了三维离散元数值模拟实验。进而采用该方法详细研究了碎屑流灾害冲击桥墩的动力响应情况以及演化规律。特别是分别研究了圆柱形桥墩以及方形桥墩对在碎屑流冲击条件下的动力响应情况，以及两种桥墩在离碎屑流的物源区不同距离时，其各自所受冲击力的演化规律。

通过离散元数值模拟可以得出，由于碎屑流本身组分主要是大小不一的碎石、砂土，碎屑流对桥墩的冲击有别于洪水对桥墩的冲击，碎屑体会在桥墩前缘产生堆积并产生静压力(方形桥墩情况)，因而方形桥墩相对于圆柱桥墩而言并不适用于碎屑流发育的沟谷地区。

相同规模的碎屑流冲击条件下，圆柱形桥墩上所受的总应力的法向应力要远小于方形桥墩所受的总应力的法向应力；虽然圆柱形桥墩上所受的总应力的切向应力要大于方形桥墩，但相对于其法向应力而言，依然要小得多。

如果忽略掉碎屑流在桥墩前缘的堆积作用，就单纯的碎屑流冲击力作为对比条件，我们可以发现不管是圆柱形桥墩上所受的碎屑流的最大冲击力，还是碎屑流的平均冲击力，都要小于相同情况下的方形桥墩上所受的冲击力，并且随着桥墩离碎屑流的物源区越远，作用在桥墩上的冲击力则越小。

本次研究证明了圆柱形桥墩更适用于碎屑流发育的沟谷区，并且给出了桥墩离碎屑流的物源区距离和桥墩所受冲击力之间的演化规律。尽管实际条件下的碎屑流冲击桥墩会产生桥墩的断裂、变形等情况，本文只考虑桥墩未受破坏条件下所受的冲击力的变化，研究重点是碎屑流和桥墩之间的动力响应规律，从而为工程实践提供一定的指导作用。而关于桥墩受到破坏后的断裂、变形等情况，将在接下来的工作中着重进行。

[1] CUI Peng, CHEN Xiaoqing, ZHU Yingyan, et al. The Wenchuan earthquake (May 12, 2008), Sichuan Province, China, and resulting geohazards[J]. Natural Hazards, 2011, 56(1): 19-36.

[2] ZHANG Ming, YIN Yueping, WU Shuren, et al. Dynamics of the Niumiangou Creek rock avalanche trigg- ered by 2008 Ms 8.0 Wenchuan earthquake, Sichuan, China[J]. Landslides, 2011, 8(3): 363-371.

[3] 毕钰璋, 付跃升, 何思明,等. 牛眠沟地震滑坡碎屑化全过程离散元模拟[J]. 中国地质灾害与防治学报, 2015, 26(3):17-25.

BI Yuzhang,FU Yuesheng,HE Siming,et al.Simulation of the whole process of Niumiangou creek rock avalanche triggered by the earthquake using a distinct element method[J].The Chinese Journal of Geological Hazard and Control,2015, 26(3):17-25.

[4] Crandell D R, Miller C D, Glicken H X, et al. Catastrophic debris avalanche from ancestral Mount Shasta volcano, California[J]. Geology, 1984, 12(3): 143-146.

[5] Cruden D M, Hungr O. The debris of the Frank Slide and theories of rockslide- avalanche mobility[J]. Canadian Journal of Earth Sciences, 1986, 23(3): 425-432.

[6] Nicoletti P G, Sorriso-Valvo M. Geomorphic controls of the shape and mobility of rock avalanches[J]. Geological Society of America Bulletin, 1991, 103(10): 1365-1373.

[7] Mudge M R. Rockfall-avalanche and rockslide-avalanche deposits at Sawtooth Ridge, Montana[J]. Geological Society of America Bulletin, 1965, 76(9): 1003-1014.

[8] 何思明, 庄卫林, 张雄, 等. 都汶公路彻底关大桥桥墩抗滚石冲击防护研究[J]. 岩石力学与工程学报, 2013, 34(2): 3421-3427.

HE Siming,ZHUANG Weilin, ZHANG Xiong, et al. Research on rockfall impact prevention of Chediguan bridge pier, Duwen road[J].Chinese Journal of Rock Mechanics and Engineering, 2013, 34(2): 3421-3427.

[9] 裴向军, 黄润秋, 李世贵. 强震崩塌岩体冲击桥墩动力响应研究[J]. 岩石力学与工程学报, 2011，(S2): 3995-4001.

PEI Xiangjun,HUANG Runqiu,LI Shigui.Study of dynamic response of bridge pier shocked by falling rock induced by intensive earthquake[J].Chinese Journal of Rock Mechanics and Engineering, 2011，(S2): 3995-4001.

[10] LI Xinpo, HE Siming, LUO Yu et al. Discrete element modeling of debris avalanche impact on retaining walls[J]. Journal of Mountain Science, 2010, 7(3): 276-281.

[11] Salciarini D, Tamagnini C, Conversini P. Discrete element modeling of debris-avalanche impact on earthfill barriers. Physics and Chemistry of the Earth, Parts A/B/C, 2010,35(3):172-181.

[12] 毕钰璋, 何思明, 付跃升,等. 基于离散元方法的高速远程滑坡碎屑流新型防护结构[J]. 山地学报, 2015，33(5):560-570.

BI Yuzhang,HE Siming,FU Yuesheng,et al.Simulation of the dynamic response of new type rock avalanche impact defense structure and the mechanism of energy dissipation base on DEM[J].Journal of Mountain Science,2015，33(5):560-570.

[13] Cundall P A, & Strack O D. A discrete numerical model for granular assemblies. Geotechnique, 1979, 29(1): 47-65.

[14] Choi C E, Ng C W W, Law R P H, et al. Computational investigation of baffle configuration on impedance of channelized debris flow[J]. Canadian Geotechnical Journal, 2014, 52(2): 182-197.

[15] Law R P H, Choi C E, Ng C W W. Discrete-element investigation of influence of granular debris flow baffles on rigid barrier impact[J]. Canadian Geotechnical Journal, 2015, 52(999): 1-7.

[16] Bi Y, He S, Li X, et al. Geo-engineered buffer capacity of two-layered absorbing system under the impact of rock avalanches based on Discrete Element Method[J]. Journal of Mountain Science, 2016, 13(5): 917-929.

Discrete-elementinvestigationofrockavalanchesimpactonthebridgepier

BI Yuzhang1,2,3, HE Siming2,3,4, WANG Dongpo2,3,5, SUN Xinpo6, YAN Shuaixing2,3,ZHOU Yubo2,3, CHEN Zheng2,3

(1.InstituteofGeotechnicalEngineering,SchoolofTransportation,SoutheastUniversity,Nanjing,Jiangsu210096,China; 2.KeyLaboratoryofMountainHazardsandEarthSurfaceProcess,ChineseAcademyofSciences,Chengdu,Sichuan610041,China; 3.InstituteofMountainHazardsandEnvironment,ChineseAcademyofSciences&WaterResourcesMinistry,Chengdu,Sichuan610041,China; 4.CenterforExcellenceinTibetanPlateauEarthSciences,ChineseAcademyofSciences,Beijing100101,China；5.StateKeyLaboratoryofGeohazardPreventionandGeoenvironmentProtection,ChengduUniversityofTechnology,Chengdu,Sichuan610059,China; 6.SichuanUniversityofScience&Engineering,Zigong,Sichun643000,China)

A rock avalanche is a very dangerous geological hazard that shows high mobility and high kinetic energy. In southwest China, rock avalanches often destroy residential areas and transportation routes especially the bridge. Despite the engineering value of avalanches, their influence on rigid barrier impact is still not well understood. A calibrated discrete element method (DEM) model using a series of flume experiments was adopted to study the dynamic response between the rock avalanches and bridge pier. The results show that the normal stress of rock avalanches exerted on cylindrical pier is obviously smaller than square pier’s. However, the value of tangential stress is higher than square pier. What is more, the maximum impact force of rock avalanches exerted on cylindrical pier is smaller than square pier’s, and the same rule is between the average impact force and two piers.

bridge pier; rock avalanche; 3D discrete element; impact force

10.16031/j.cnki.issn.1003-8035.2017.04.03

U443.22

A

1003-8035(2017)04-0016-06

2017-02-20;

2017-03-06

国家自然科学基金(41472325； 41502297)； 四川省科技支撑计划项目(2016SZ0067); 四川省重点研发计划(2017SZ0041)

毕钰璋(1990-)，男，博士研究生，主要从事滑坡、崩塌方面的研究。E-mail: biyuzhang@imde.ac.cn

何思明(1968-)，男，研究员，主要从事滑坡机理和关键技术研究。E-mail: hsm@imde.ac.cn