配电网可靠性评估与优化系统重构算法

臧志斌，郑培昊，魏本海，翟再培，马胜国



配电网可靠性评估与优化系统重构算法

臧志斌，郑培昊，魏本海，翟再培，马胜国

（深圳市国电科技通信有限公司，广东 深圳 518000）

基于配电网可靠性和网络重构方面的研究，提出了一种考虑配电网可靠性下的重构快速方法。首先通过对可靠性指标体系研究，确定以有功网络损耗（LOSS）、系统供电量不足（ENS）和平均供电可用率（ASAI）作为评价指标体系，并进行了归一化构建配电网多目标模型，运用判断矩阵法将多目标函数转化为新的单一目标函数，实现对配电网系统的重构优化快速计算。算法在重构后期引入可靠性评估，提高了配电网最优解的求解效率。通过IEEE69算例验证了新的配电网重构优化算法在获得全局最优解的同时，降低了计算时间，能有效解决复杂网络的重构优化问题。

可靠性评估；配电网重构；有功网络损耗

1 引言

配电系统是电力输送的核心环节，其供电可靠性对于生产生活都有直接影响[1-3]。配电系统中通过有效技术手段降低故障发生率、线损率等满足供电要求。而配电网中存在大量隔离开关、断路器等设备，在电网运行或检修过程中，调度人员断开或接通隔离开关来调整电网络结构，这种方式即网络重构，配网重构主要用来均匀负荷、降低线损、消除过载，降低系统复杂度和供电质量[4]，是配电管理系统的一项主要内容。

目前相关学者针对配电网可靠性研究和重构优化进行了多方面研究[5-8]。如基于配电系统可靠性评估中提出解析法[9,10]（故障树分析法（FTA）、网络等值法（NE）等）、模拟法和组合法。这些研究方法各有优势，如解析法具有精确度高、计算简单等优势，但不能提供可靠性指标的动态变化特征[11]；模拟法能获取更多的指标信息，但存在模拟时间长等缺陷[12]；组合法计算速度快，计算简单，但计算量大，且可靠性指标受到一定限制[13]。而基于配电网重构算法中可分为传统算法和现代算法，其中典型的有支路交换法[14]、随机类算法[15]、最优流法[16]等。传统优化算法中在求解全局最优解时缺乏一个统一标准，而现代人工智能算法存在计算时间长且易局部最优的问题。

从上述研究中可以看出，当前对配电网可靠性和重构优化的研究更多的是独立进行的，并未实现配电网可靠性评估下的网络重构优化的系统化研究。且针对配电系统元件多、结构复杂的特征，采用传统的评估方式和重构法可能造成效率低下、解的精度下降等问题。本文提出了一种考虑配电网可靠性的网络重构快速方法，构建了基于可靠性指标的多目标模型，实现配电网重构的经济性和可靠性。

2 配电网可靠性指标体系

配电网重构的目标是提高供电质量、降低网损、平衡负荷。系统网损越低，配电网负荷越平衡、节点分布电压越均匀[17]。而有功网损同时是配电网经济可靠性的重要指标，随着用户对供电可靠性的进一步提高，表征配电网可靠性指标主要分为系统可靠性指标和负荷点可靠性指标。

系统可靠性指标主要分为两类，即基于负荷电量的能量指标以及基于用户的概率类指标[18]。与用户有关的系统可靠性指标重点关注系统间用户平均断电频率和系统平均停电频率，描述的是停电次数和电网平均停运持续时间指标。与负荷电量能量有关的指标侧重于电网内总供电不足，考虑的是系统总供电量对用户电量的影响。系统可靠性指标的结构层次如图1所示。

图1 配电网可靠性指标结构层次

3 考虑可靠性的重构优化新模型

3.1 重构优化目标函数

传统配电网重构通常是基于系统有功网损优化的目标函数[19]。综合考虑配电网系统和负荷点可靠性指标体系，采用系统可靠性指标作为重构目标函数来反映系统结构可靠性优劣。同时，考虑到系统可靠性指标体系中的指标基本都是针对同一个问题提出的不同描述方式，利用其中任意一个指标来描述系统可靠性都满足描述要求，且不同类指标存在关联性，任意两个指标都能表征出其他指标值。综合考虑传统配电网中的有功网损指标，选用平均供电可用率（average service availability index，ASAI）和系统供电量不足（ENS）、有功网损（LOSS）3个指标作为配电网络重构优化的目标函数。

考虑到选定的3个指标是3个不同的量纲，因而在对选定的3个指标优劣度进行比较时，不能简单地通过数据对比来实现量值比较，在构建网络重构模型前，需要对不同量纲指标进行归一化处理，构造满意度评估函数。

（1）有功网损指标

网络重构中，为保证系统的经济性和电能质量，要求系统有功网损保持在低水平。为反映重构方案中有功网损存在的差异性，构造基于系统有功网损的满意度评估函数对不同重构方案进行评价，为：

（2）平均供电可用率指标

指标直接反映故障对生产生活的影响程度。理论上配电系统不可能达到1.0的水平。配电网实际运行过程中，平均供电可用率指标在0.99附近表征效果更明显。根据指标特点，确定指标的满意度评估函数为：

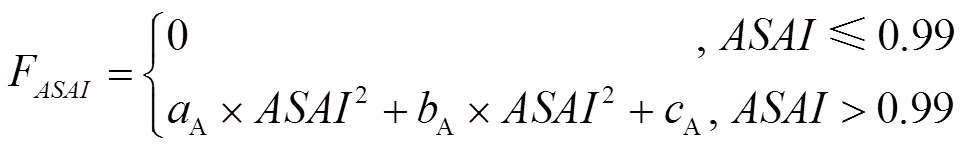
（3）系统供电量不足指标

表征配电网总供电能不足，直接反映故障的影响范围，是系统经济损失的指标之一。通常这一指标为系统平均总有功的5~10倍，指标的满意度和取值为线性关系，确定指标的满意度评估函数为：

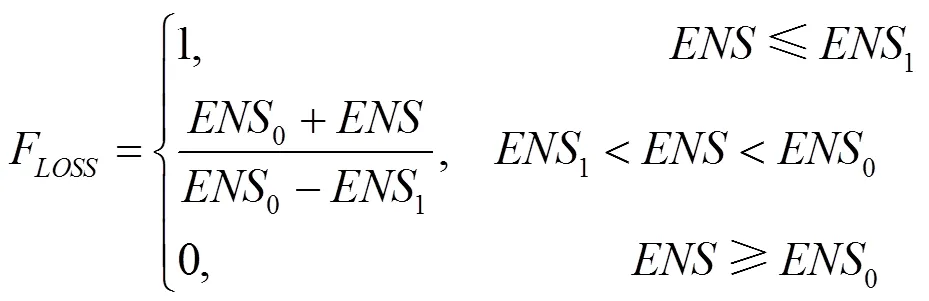
3.2 目标函数约束条件

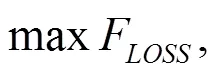
重构后的配电网模型除满足基本的“回路”和“孤岛”的约束外[20]，同时需要满足以潮流方程等式约束、支路传输功率约束、节点电压约束的约束条件。

潮流方程等式约束条件为：

节点电压约束条件为：

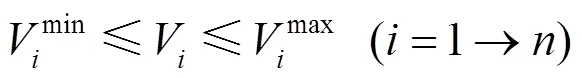
支路传输功率约束条件为：

3.3 目标函数的处理

配电网重构优化模型是一个多目标规划问题，且各目标的重要程度不同，为将多目标问题转化为单目标求解，采用判断矩阵法[21]进行转化。

由判断矩阵法，根据重要性不同将不同目标分为3个等级：系统供电量不足是衡量经济损失的一个主要指标，平均供电可用率反映供电故障对生产生活的影响效果，这两个指标侧重的是对供电效应的描述，将其作为第二等级目标；有功网损反映配电网系统的运行状态，是供电、配电和用电方面的综合反映指标，因此将其作为最重要的第一等级目标。不同等级目标重要性不同，其中第一等级最重要，往后次之。同一等级目标具有相同的重要性。

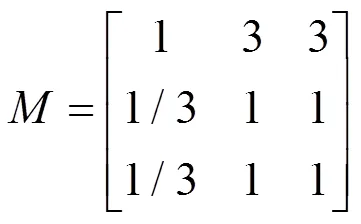
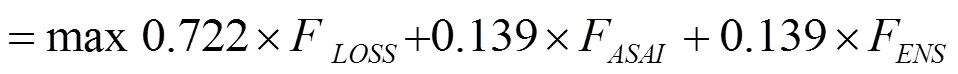
4 重构算法的优化求解

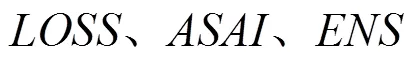
针对新模型的特点，按以下设计思路进行可靠性前提下的配电网重构求解。

（1）重构前期仅计算系统的有功网损，不考虑配电网的可靠性计算机，以有功网损作为判断网络方案优劣性的唯一准则，确定最优方案。

（2）重构后期，引入对配电网负荷点和系统可靠性指标的计算，通过式（9）计算获得函数的最大目标值，寻找最优方案的最优解。

求解过程中，以有功网损的变化来作为网络重构前期、后期判断依据：重构前期有功网损的变化幅度大。当连续3次重构结构获得的有功网损降幅大于3%时，定义为网络重构前期；当连续3次获得的有功网损降幅小于3%时，则为重构后期。

4.1 算法流程

考虑到配电网系统有功网损和可靠性指标的特点和相互关联性，结合新模型的求解思路，构造基于配电网可靠性的网络重构计算法则，算法的详细的计算步骤如下。

步骤1 配电系统基本参数的读取和算法控制参数的输入，设置重构计算标识符：=1。

步骤2 根据式（1）~式（3）分别计算网络系统中的有功网损、系统供电量不足、平均供电可用率3个指标的满意度评估函数。

步骤3 计算配电网的初始有功网损。计算连续3次的有功网损变化幅值，判断重构计算处于何种阶段。

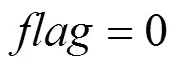
步骤5 判断重构结果的收敛性，若结构收敛，则计算结束，输出计算结果；若结构不收敛，则返回步骤3继续寻优。

4.2 算例分析

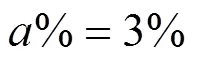
表1 元件可靠性参数

4.2.1 结果分析

图2 IEEE69节点配电系统

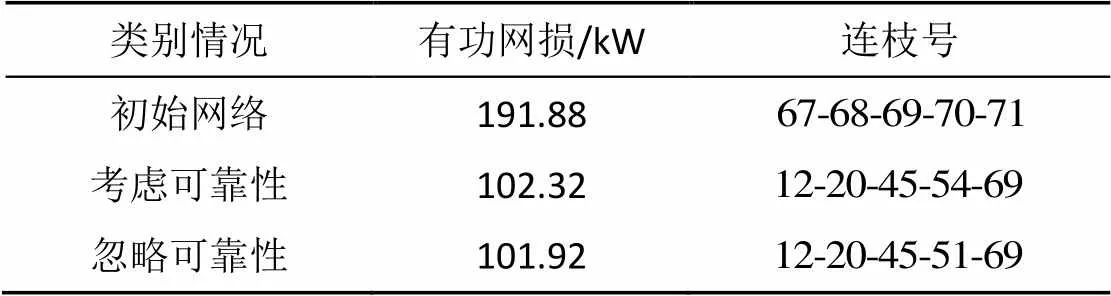
表2 不同情况下的重构结果

表3为可靠性前后的网络重构目标函数值。从表3中获得的结果可知，配电网系统在可靠性前的满意度为0.65，配电网系统运行的有功网损为101.82 kW，而考虑可靠性后获得的满意度为0.63，配电网系统运行有功网损为102.63 kW。对比可靠性前后的满意度和有功网速可知，二者差别不大。但和就体现出了较大差别，可靠性前的实际值为0.988 9，满意度为0，实际值为7.621 3，满意度为0.51，可靠性后的实际值为0.993 1，满意度为0.68，实际值为6.843 1，满意度为0.60。可靠性前后的提高0.004 2，满意度提高0.68；指标提高0.778 2，满意度提高0.09。对比分析可知，在配电网重构中加入可靠性指标能明显提高系统的可靠性。从新的总目标函数看，尽管配电网系统的有功网损满意度出现了一定程度的下降，但得到了提高，可靠性后新的目标函数总满意度提升到0.632 1，因而重构后的系统在可靠性和经济性方面都有了很大提升。

表3 不同情况下指标对比结果

4.2.2 算法性能分析

表4为加入可靠性指标后重构过程中，利用本文提供的计算方式和单一的可靠性指标计算获得的对比结果。从结果中可以看出，两种计算方式获得的结果是完全相同的，表明本文中提出的简化型算法是可取的。且新算法耗时14.62 s，而采用单一的可靠性指标计算耗时39.21 s，相较于新算法耗时有明显增长，因此，采用本文中提出的新算法在保证结果精确度的同时也大大提高了计算效率，优势明显。

表4 算法的计算对比结果

为分析可靠性指标对计算效率效率的作用，模拟了不同有功网损降幅下可靠性指标迭代次数和收敛到最优解的计算时间。从获得的结果可以看出，不同有功网损降幅下的结构都能得到最优目标函数值，但迭代次数和收敛计算时间有一定差异性，其中直接加入可靠性指标和网损降幅分别为6%、8%和10%条件下的迭代次数均为12次。而1%网损下的迭代次数达到20次，这是由于寻优初期，有功网损下降，系统的可靠性升高，而较小有功网损下网络结构的调整易导致迭代网损剧烈变化，迭代次数增加，整体来讲，有功网损降幅与迭代次数成反比。有功网速在3%时的迭代次数为14次。

表5 指标对计算时间和迭代次数的影响

收敛最优解计算时间方面，1%有功网损下的计算时间最长，其后依次是直接接入和10%和8%有功网损下的收敛计算时间依次递减。在3%下的收敛计算时间最少，这是因为尽管新算法的迭代次数高于大有功网损，但算法前期不许对可靠性指标进行计算，所以计算收敛时间更少。

5 结束语

本文在对传统配电网可靠性研究基础上，在配电网重构优化中引入系统可靠性指标，构建了基于可靠性指标的多目标模型，实现对配电网系统可靠性和重构优化的快速计算，提高了算法的效率和经济型。本文主要结论如下。

• 建立了可靠性指标的配电网重构模型。以AISI、ENS可靠性指标和有功网损最小为目标函数，对多目标函数进行归一化处理，符合实际网络重构需求。

• 建立基于多目标函数的快速算法。通过判断矩阵法将多目标函数转化为新的单一目标函数，在重构后期加入可靠性指标的重构优化计算中，提高了配电网最优解的求解效率，降低了求解计算时间。

• 通过IEEE69算例验证表明，本文提出的配电网重构优化算法同时满足了网络可靠性和经济型需求，算法在获得全局最优解的同时降低了计算时间，能有效解决复杂网络的重构优化问题。

[1] 陈雪, 黄伟, 叶琳浩, 等. 基于多源数据的配电网规划辅助决策系统研究[J]. 广东电力, 2017, 30(1): 53-58.

CHEN X, HUANG W, YE L H, et al. Based on multi-source data of distribution network planning assistant decision-making system research[J]. Journal of Guangdong Electric Power, 2017, 30(1): 53-58.

[2] 马钊, 刘颖异, 尚宇炜, 等. CIGRE 2016未来电力系统及主动配电系统技术新动向[J]. 中国电机工程学报, 2017, 37(1): 27-36.

MA Z, LIU Y Y, SHANG Y W. CIGRE 2016 new trends of the future power system and the active power distribution system technology[J]. Proceedings of the CSEE, 2017, 37(1): 27-36.

[3] 汪芳宗, 王兆丰. 基于混合整数二次锥规划方法的含分布式电源配电网优化重构方法[J]. 电力系统保护与控制, 2016, 44(24): 24-30.

WANG F Z, WANG Z F. Based on mixed integer quadratic cone programming method of distributed power distribution network optimization reconstruction method[J]. Power system protection and control, 2016, 44(24): 24-30.

[4] 邱骁奇, 胡志坚. 基于改进教与学优化算法的配电网重构[J]. 电力系统保护与控制, 2016, 44(12): 42-49.

WIU X Q, HU Z J. Based on the improvement of the power grid reconstruction of the improved teaching and learning algorithm[J]. Power System Protection and Control, 2016, 44(12): 42-49.

[5] 李春燕, 许中, 马智远. 计及用户需求响应的分时电价优化模型[J]. 电力系统及其自动化学报, 2015, 27(3): 11-16.

LI C Y, XU Z, MA Z Y. Optimization model of time-sharing electricity meter and user demand response[J]. Journal of Electric Power System and its Automation, 2015, 27(3): 11-16.

[6] 段聪. 计及风电出力优化或电动汽车充电站规划的配电网重构[D]. 北京：华北电力大学, 2015.

DUANG C.The distribution grid reconstruction of power plant optimization or electric vehicle charging stations[D]. Beijing: North China electricity university, 2015.

[7] 靳小龙, 穆云飞, 贾宏杰, 等. 面向最大供电能力提升的配电网主动重构策略[J]. 电工技术学报, 2014, 29(12): 137-147.

JIN X L, MU Y F, JIA H J, et al. For maximum power supply ability of ascension active distribution network reconfiguration strategy[J]. Journal of Electro Technics, 2014, 29(12): 137-147.

[8] 孙元博. 基于图解蚂蚁系统算法的城市配电网重构与故障恢复综合方法研究[D]. 武汉: 武汉大学, 2014.

SUN Y B. A comprehensive approach to the reconstruction and failure recovery of the urban distribution network based on the graphical ant system algorithm[D]. Wuhan: Wuhan University, 2014.

[9] 孙惠娟, 彭春华, 余廷芳. 配电网三相平衡优化重构策略[J]. 电网技术, 2014, 38(3): 789-794.

SUN H J, PENG C H, YU T F. The three-phase balance optimization reconstruction strategy[J]. Power Grid Technology, 2014, 38(3) : 789-794.

[10] 何禹清, 毛丽林, 苏黎, 等. 配电网可靠性评估及重构优化系统的设计[J]. 电力系统及其自动化学报, 2013, 25(6): 148-153.

HE Y Q, MAO L L, SU L, et al. Distribution network reliability assessment and optimization system of reconfiguration design[J]. Journal of Electric Power System and its Automation, 2013, 25(6): 148-153.

[11] 刘畅, 黄民翔. 含多种分布式电源的配电网重构优化研究[J]. 电力系统保护与控制, 2013(6): 13-18.

LIU C, HUANG M X. The optimization of the power distribution of distributed power supply[J]. Power System Protection and Control, 2013(6): 13-18.

[12] 江东林, 刘天琪, 李樊. 采用时段动态划分和分层优化策略的配电网重构[J]. 电网技术, 2012, 36(2): 153-157.

JIANG D L, LIU T Q, LI F. With time dynamic partitioning and hierarchical optimization strategy of distribution network reconfiguration[J]. Power Grid Technology, 2012, 36(2): 153-157.

[13] 梁伟宸, 唐爱红. 分布式电源的配电网重构和电容器优化投切[J]. 中国电力, 2011, 44(8): 26-30.

LIANG W C, TANG A H. The distribution power grid refactorings and capacitors of distributed power supply[J]. China Power, 2011, 44(8): 26-30.

[14] 何宏杰. 基于二进制粒子群优化算法的配电网重构研究[D]. 杭州: 浙江大学, 2006.

HE H J. The research of the distribution grid reconstruction of binary particle swarm optimization algorithm[D]. Hangzhou: Zhejiang University, 2006.

[15] 王大为, 朴在林. 基于序优化和模糊蚁群算法的多目标配电网重构[J]. 电网与清洁能源, 2016, 32(9): 44-49.

WANG D W, PIAO Z L. Based on the sequence optimization and fuzzy multi-objective distribution network reconfiguration of ant colony algorithm[J]. Power Grid and Clean Energy, 2016, 32(9): 44-49.

[16] 邵静. 基于短期负荷预测的含分布式发电配电网重构[D]. 成都: 西南交通大学, 2015.

SHAO J. Reconstruction of distributed generation power grid based on the short-term load forecast[D]. Chengdu: Southwest Jiaotong University, 2015.

[17] 卞栋, 卫志农, 黄向前, 等. 电力市场中含分布式电源的配电网重构模型[J]. 电力系统保护与控制, 2013(11): 117-123.

BIAN D, WEI Z N, HUANG X Q, et al. Including the distributed power distribution network reconfiguration in power market model[J]. Power System Protection and Control, 2013(11): 117-123.

[18] 陈萍, 毛弋, 童伟, 等. 基于多目标粒子群算法的配电网多目标优化重构[J]. 电力系统及其自动化学报, 2016, 28(7): 68-72.

CHEN P, MAO Y, TONG W, et al. Based on multi-objective particle swarm algorithm of the multi-objective optimization distribution network reconstruction[J]. Journal of Electric Power System and its Automation, 2016, 28(7): 68-72.

[19] 易海川, 张彼德, 王海颖, 等. 提高DG接纳能力的配电网动态重构方法[J]. 电网技术, 2016, 40(5): 1431-1436.

YI H C, ZHANG B D, WANG H Y, et al. Improve the ability of DG acceptance of dynamic distribution network reconfiguration method[J]. Power grid technology, 2016, 40(5): 1431-1436.

[20] 黄红程, 顾洁, 方陈. 基于无向生成树的并行遗传算法在配电网重构中的应用[J]. 电力系统自动化, 2015(14): 89-96.

HUANG H C, GU J, FANG C. Parallel genetic algorithm based on undirected spanning tree in the application of distribution network reconfiguration[J]. Automation of Electric Power Systems, 2015(14): 89-96.

[21] 朱磊. 配电网重构过程中无源滤波器稳定运行研究[D]. 合肥: 安徽大学, 2013.

ZHU L. The stable operation of passive filters in the grid reconstruction process[D]. Hefei: Anhui University, 2013.

[22] 易波, 刘建华, 周雄, 等. 基于二次协作优化方法的配电网重构[J]. 电力科学与技术学报, 2012, 27(4): 46-50, 56.

YI B, LIU J H, ZHOU X, et al. Collaboration based on quadratic optimization method of distribution network reconfiguration[J]. Journal of electric power science and technology, 2012, 27(4): 46-50, 56.

[23] 邹必昌, 龚庆武, 李勋. 基于负荷平衡的配电网重构遗传算法研究[J]. 电力系统保护与控制, 2011, 39(6): 80-83, 111.

ZOU B C, GONG Q W, LI X. Distribution network reconfiguration based on load balancing genetic algorithm[J]. Power System Protection and Control, 2011, 29(6): 80-83,111.

Algorithm of grid reliability assessment and reconstruction optimization system

ZANG Zhibin, ZHENG Peihao, WEI Benhai, ZHAI Zaipei, MA Shengguo

Shenzhen Guodian Science and Technology Communication Co., Ltd., Shenzhen 518000, China

Based on the research of the reliability of distribution network and the reconstruction of network, a new method was put forward to reconstruct the power grid reliability. Firstly, the evaluation index system was proposed, which included the active network LOSS (LOSS), lack of system power supply (ENS) and the average power supply availability (ASAI). A multi-objective model of distribution network was constructed by normalization, and the multi-objective function was transformed into a new single objective function by using the judgment matrix method, which realized fast calculation of power distribution network reconstruction and optimization. Through IEEE69 example verification, the optimization algorithm can obtain the global optimal solution and reduce the computational time at the same time, effectively solve the problem of the reconstruction of the complex network optimization.

reliability assessment, grid reconstruction, active network loss

TN929

A

10.11959/j.issn.1000−0801.2017344

2017−10−10；

2017−11−30

山地城市电动汽车分时租赁模式及支撑技术研究与示范应用（No. 2015BAG10B00）

Research and Demonstration Application of Time Sharing Leasing Model and Supporting Technology for Electric Vehicles in Mountain Cities (No. 2015BAG10B00)

臧志斌（1974−），男，深圳市国电科技通信有限公司高级工程师，主要从事用电信息采集系统、电动车运营服务平台、电能计量与采集应用研究、新能源汽车产业发展规划方面的工作。

郑培昊（1978−），男，深圳市国电科技通信有限公司副高级工程师，主要研究方向为电动汽车充换电技术、电力系统自动化、智能电网、新能源汽车产业发展规划。

魏本海（1974−），男，深圳市国电科技通信有限公司高级工程师，主要研究方向为电动汽车充换电技术、智能用电技术、电力系统自动化和智能电网。

翟再培（1988−），男，深圳市国电科技通信有限公司工程师，主要研究方向为电动汽车服务平台技术、配网自动化和大数据。

马胜国（1985−），男，深圳市国电科技通信有限公司工程师，主要研究方向为电动汽车服务平台技术、电能计量与采集应用研究、智能用电技术等。