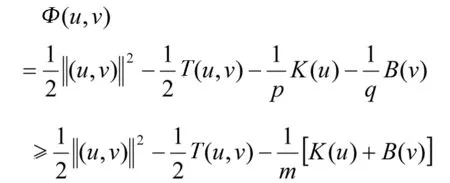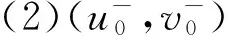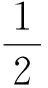一类具有次临界指数方程组解的存在性研究

马世龙

(哈尔滨师范大学)

一类具有次临界指数方程组解的存在性研究

马世龙

(哈尔滨师范大学)

主要研究一类具有次临界指数方程组解的存在性，证明中的主要原理是利用Nehari流形方法说明方程组解的存在性.

Nehari流行；次临界指数；椭圆方程组

0 引言

该文考虑如下椭圆方程组

其中x∈Ω⊂Rn(n≥3)是一个具有光滑边界额有界区域,α,β,γ∈R,α>0,γ>0,β2-αγ<0,2

0<λ1≤λ2，αu2+2βuv+γv2≥0，且

λ1(u2+v2)≤αu2+2βuv+γv2≤λ2(u2+v2)

(2)

其中α>0,γ>0,β2-αγ<0.

近年来，关于利用Nehari流形证明含有临界指数或次临界指数方程组解的存在性得到了广泛的研究.樊自安[1]研究了如下方程组

解的存在性，得到了当0<λ1≤λ2<η1,2

1 主要结果

定义1.1 (u,v)∈E是方程组(1)的一个弱解是指任意的(ω1,ω2)∈E满足：

定理1.2 假设0<λ1≤λ2<η1，2

2 定理1.2证明

定义能量函数：

则Φ(u,v)∈C1(E,R),考虑Nehari流形

Mλ={(u,v)∈E(〗(0,0)}|〈Φ′(u,v),(u,v)〉=0}

所以(u,v)∈Mλ当且仅当

〈Φ′(u,v),(u,v)〉=‖(u,v)‖2-T(u,v)-K(u)-B(v)=0

(4)

对于(u,v)∈Mλ

则Φ(u,v)有下界.

定义Γ(u,v)=〈Φ′(u,v),(u,v)〉 .

对于(u,v)∈Mλ

〈Γ′(u,v),(u,v)〉

=2(‖(u,v)‖2-T(u,v))-pK(u)

-qB(v)

=(2-p)K(u)+(2-q)B(v)<0.

把Mλ分成三个部分

Φ′(u0,v0)=0，即(u0,v0)是Φ(u,v)的一个临界点.

证明证明过程参考文献[7].

其中，m=min{p,q}.

由(4)， 所以

其中n=max{p,q}

则由(5)，(6)有

于是由(7)可得到ξ->1.

证明设(u,v)∈E且K(u)>0，B(v)>0设

h′(t)=t[‖(u,v)‖2-T(u,v)]-tp-1K(u)-tq-1B(v)

令h′(t)=0即

t[‖(u,v)‖2-T(u,v)]-tp-1K(u)-tq-1B(v)=0

得到t=t0=1，h(0)=0，t→-∞，h(t)→-∞，当t∈[0,t0=1)，h′(t0)>0，当t∈[t0=1,

+∞),h′(t0)<0.

因此h(t)在t=t0处达到最大值.

由(5)有

其中m=min{p,q}.

所以当n→∞，

或

(8)

[1] 樊自安. 包含次临界和临界Sobolev指数的椭圆方程组解的存在性. 应用数学学报,2015(9): 835-844.

[2] 樊自安. 包含次临界和临界Sobolev指数的Schr"{o}dinger-Possion方程的正解. 数学的实践与认识,2017(6):247-254.

[3] Alves C O, Morais Filho, Souto D C, et al. On systems of elliptic equations involving subcritical or critical Sobolev exponents. Nonlinear Analysis,2000,42: 771-787.

[4] Liu Z, Han P G. Existence of solutions for singular elliptic system with critical exponents. Nonlinear Analysis: Theory, Methods&Applications, 2008,69(9): 2968-2983.

[5] Hsu T S,Li H L. Multiplicity of positive solutions for singular elliptic systems with critical Sobolev-Hardy and concave exponents[J]. Acta Mathematica Scientia , 2011,31(3): 719-804.

[6] 张文丽. 一类奇异临界的(p,q)-Laplacian拟线性方程组非负基态解的存在性. 系统科学与数学,2014(5): 602-611.

[7] Brezis K J, Zhang Y. The Nehari manifold for a semilinear elliptic problem with a sign changing weight function[J]. J Differential Equations ,2003,1993:481-499.

AKindofExistenceStudyofSolutionstotheSystemofSubcriticalExponentialEquations

Ma Shilong

(Harbin Normal University)

In this paper, the existence of solutions to the system of subcritical exponential equations is mainly studied. The main principle of the proof is to illustrate the existence of solution of equations by using Nehari manifolds.

Nehari manifold; Subcritical exponents; Elliptic systems

于达)

O175.25

A

1000-5617(2017)04-0014-04

2017-07-03