移动应用众包测试人员评价模型

刘 莹，张 涛，李 坤，李 楠

(西北工业大学 软件与微电子学院, 西安 710072)

移动应用众包测试人员评价模型

刘 莹*，张 涛，李 坤，李 楠

(西北工业大学 软件与微电子学院, 西安 710072)

移动应用众包测试人员具有匿名、非契约的特性，这使得任务发布者难以准确评估众包测试人员的能力与测试质量。针对该问题，提出了一种移动应用众包测试人员层次分析法(AHP)评价模型。该模型从活跃度、测试能力、诚信度等多指标分层综合评估众包测试人员能力，通过构造判断矩阵、一致性检验计算各层次指标的组合权重向量，并引入需求列表与描述列表改进本模型，使测试人员与众包任务更加匹配。实验结果表明，所提模型能够实现对测试人员能力的准确评估，支持基于评估结果的众包测试人员选择与推荐，提高了移动应用众包测试效率与质量。

移动应用众包测试；人员评价；层次分析法；皮尔逊相关性系数；斯皮尔曼相关系数

0 引言

移动应用众包测试是一种分布式问题解决方案，将过去由员工执行的测试任务以自由自愿的方式外包给匿名网络用户[1-2]。与传统外包相比，众包具有自由、高创新度、低成本等优势。但由于众包测试人员是匿名的，且未与企业签订协议，导致众包测试的质量难以保证[3]。随着移动应用众包测试的快速发展，对移动应用众包测试人员的准确评价，对于保证众包测试的质量尤为重要。

目前国内外针对众包人员的评价研究甚少，而现有众包测试研究主要集中在众包人员的任务推荐:Ambati等[4]建立了众包人员的偏好模型;Yuen等[5]创建“众包人员-众包任务”矩阵，并将概率矩阵分解以实现众包任务的个人偏好推荐。同时也有不以众包人员的兴趣偏好作为唯一任务推荐依据的研究:Geiger等[6]通过对相应的学术文献进行系统评价提出了个性化任务推荐机制;Ho等[7]为实现众包任务发起者利益最大化提出了两阶段探索分配算法;李勇军等[8]提出了技术能力匹配算法、非技术能力匹配算法以及综合匹配算法;肖江辉[9]从测试人员可信度的角度进行评价，集成主客观可信度从而得到可信度计算模型。但以上研究仅与众包任务推荐相关，不能用于对众包人员的评价。

国内外学者也对其他领域的人员评价方法有所研究:Woodruff[10]通过大量数据分析汇总出数据处理人员的工作绩效评估方法;Bolton[11]通过分析学校管理人员工作中可能出现的问题而对其进行评价;陈龙猛[12]设计了对实验技术人员工作评价的数学模型;杨振英等[13]运用目标-结构法构建了军队人员信息安全素养评价指标评价体系。但是以上人员评价方法不具有普适性，不能直接运用于对移动应用众包人员的评价。

本文针对移动应用众包测试人员评价问题，应用层次分析法(Analytic Hierarchy Process, AHP)构建移动应用众包测试人员能力综合评价模型。首先定义分层的众包测试人员评价指标体系，构造对比矩阵并经过一致性检验，获得组合指标权重，并引入需求列表、描述列表对本模型进行优化，实现对移动应用众包测试人员的准确评价。

1 移动应用众包测试人员评价模型

1.1 层次分析法简介

层次分析法(AHP)，也称层级分析法[14]，是一种定性与定量结合的分析方法，多用于解决存在多目标以及不确定性和主观信息的复杂问题[15]。

层次分析法的基本步骤如下：

1)建立层次结构模型。在分析问题的基础上，将问题的各影响因素分为不同的层级，明确各级因素之间的相互作用，建立多层级的指标层，应注意层次分析结构中的每层元素个数一般不超过9个，因为同一层次中包含过多元素会给元素两两比较带来不便。

2)构造因素对比判断矩阵。将处在同一层级且对同一上级指标有影响的各因素指标两两对比，依次构成对比矩阵，并将对比矩阵A以式(1)表示:

(1)

其中aij为因素i相对因素j而言的重要程度对比结果,aij的值越大表明因素i相对因素j而言越重要。

3)计算权重向量。对每一对比矩阵进行计算，得出各矩阵的最大特征根及对应特征向量。对所得结果利用一致性指标进行一致性检验，若一致性检验通过，则将特征向量进行归一化计算后得出该组因素的权重向量；若一致性检验未通过，则返回步骤2)。

4)计算各层次组合权重向量。同样对所得结果进行一致性检验，若检验通过，则可根据最终因素权重向量对结果进行决策，若检验未通过则重新构建对比矩阵或重新选择研究方法。

1.2 众包测试人员的层次评价模型

目前国内外对于众包人员的评价研究较少，本文结合移动应用测试的特性，基于现有移动应用众包测试平台人员组织管理方法，得出了如图1所示的移动应用众包测试人员评价指标体系，共有3个一级指标(B1～B3)和11个二级指标(C1～C11)。

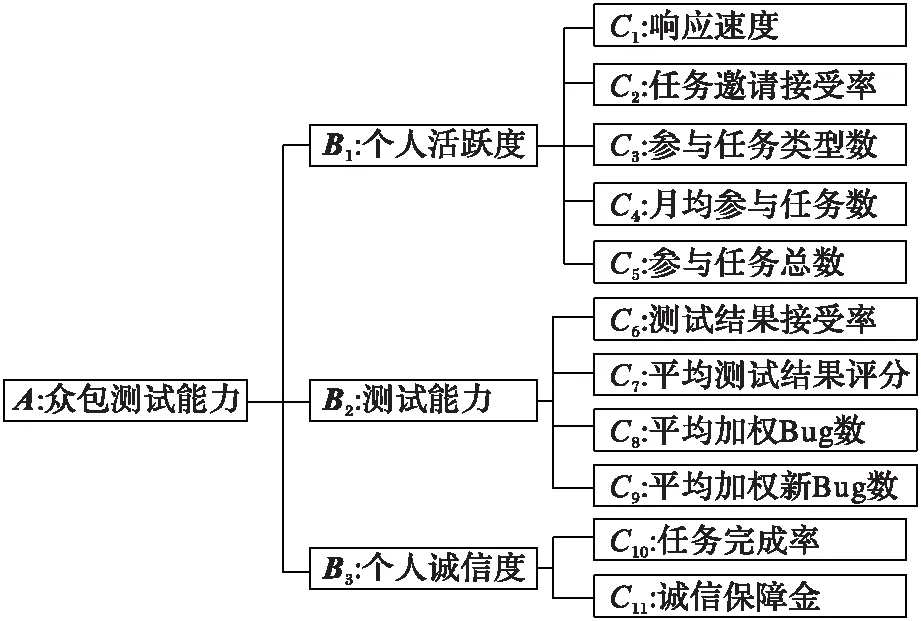
图1 移动应用众包测试人员评价指标体系Fig. 1 Evaluation index system of mobile application crowdsourcing testers

1.3 评价指标定义

1)个人活跃度体现了测试人员的效率与参与任务的数量。主要包括测试人员对任务的响应速度、响应率以及历史测试记录中涉及的任务类型数目、月平均参与任务数目和所有参与任务总数。其中响应速度(Response Speed, RS)为：

RS=(Ddue-Daccept)/(Ddue-Dcreate)

(2)

式中：Ddue中为任务的截止日期；Daccept为测试人员接受任务的日期；Dcreate为任务创建的日期。

响应率(Response Rate, RR)表示任务的接受率，定义为：

RR=Naccept/Ninvited

(3)

式中：Naccept为测试人员接受的任务数目;Ninvited为测试人员接收到邀请的任务总数。

2)个人测试能力是对测试人员最重要的评价指标，因为其直接决定测试质量的高低,主要包含客户对测试人员测试结果的接受率、测试结果的平均分、平均加权Bug数、平均加权新Bug数。其中结果接受率(Result Accept Rate, RAR)定义为：

RAR=Naccepted/Nall

(4)

式中:Naccepted为客户认可的测试结果数目;Nall为测试人员完成的测试总数。

根据客户对测试人员测试结果的认可程度，将满意度分为四个等级：非常满意、满意、一般、不满意。定义客户满意度(Customer Satisfaction Rating, CSR)表达式为CSR=csrj(j=1,2,…,4)，其中csr1=5，csr2=4，csr3=3，csr4=0，则测试结果平均分(Average Test Result Score, ATRS)定义为：

(5)

其中：resulti表示第i(i∈[1,n])个测试结果;csrj表示第j(j∈[1,3])级客户满意度。

根据Bug的影响力可以将其划为不同等级：特别重要、重要、一般、不重要、不是Bug。Bugi为发现的第i个Bug，Bug严重等级(Bug Severity Level, BSL)的表达式为BSL=bslj(j=1,2,…,5),其中bsl1=5，bsl2=2，bsl3=1，bsl4=0.5，bsl5=0。

平均加权Bug数(Average Weighted Bug Number, AWBN)可以定义为：

(6)

其中newbugi为发现的第i个新Bug，则平均加权新Bug数(Average Weighted New Bug Number, AWNBN)可定义为：

(7)

3)测试人员在众测平台的个人诚信度是对其评价的另一重要指标。因为测试人员并未与众包测试平台及客户签订严格的劳动协议，测试人员可能因为各类原因无法完成测试任务，甚至会恶意欺诈，这就可能对测试质量造成极其严重的影响。其中任务完成率(Task Completion Rate, TCR)定义为：

TCR=Ncompleted/Napplied

(8)

式中：Ncompleted表示测试人员完成的所有测试任务数目；Napplied表示测试人员申请的所有测试任务数目。

1.4 构建众包测试人员多因素判断矩阵

A表示众包测试能力，B表示影响A的所有一级指标：个人活跃度B1，个人测试能力B2，个人诚信度B3。将三个一级指标两两对比，使用7分位比率排定各指标的相对优劣等级，经专家打分，得出A相对于一级指标的判断矩阵：

(9)

C表示11个二级指标。同理可得出个人活跃度B1、个人测试能力B2、个人诚信度B3的判断矩阵分别如式(10)～(12)所示:

(10)

(11)

(12)

1.5 移动应用众包测试人员指标权重向量计算

为使层次分析法所得结果符合逻辑，还需对判断矩阵进行一致性检验。一致性检验步骤如下：

步骤1 求判断矩阵的最大特征值及特征向量。

步骤2 计算一致性指标CI=(λmax-n)/(n-1)与平均随机一致性指标RI。并规定CR=CI/RI，若CR<0.1，则认为该判断矩阵具有满意一致性；若CR=0，则该判断矩阵具有完全一致性。

步骤3 若判断矩阵具有满意一致性，则λmax对应的特征向量即为该特征向量所对应的权重向量；若不具有满意一致性，则修改原矩阵直到具有满意一致性，再求其权重向量。

以判断矩阵A-B为例进行计算，得出其最大特征值λmax=3.018 4，CI=(λmax-3)/(3-1)=0.009 2，RI=0.58，并计算出CR=CI/RI=0.015 9<0.1，这说明A-B具有满意一致性，对应的特征向量即为该特征向量所对应的权重向量。

同理得出一级指标B1、B2、B3的归一化权重、最大特征值λmax以及一致性验证指标CR如表1所示。

通过以上计算可知各判断矩阵具有满意一致性，汇总各判断矩阵的特征向量，得到指标权重表，如表2所示。

1.6 评价指标的各层次组合权重向量计算

由表2中的数据可以得出，众包测试能力与其对应的三个一级指标模型如下：

A=0.117×B1+0.615×B2+0.268×B3

(13)

三个一级指标与其对应二级指标模型如式(14)～(16)所示：

B1=0.084×C1+0.244×C2+0.479×C3+

0.044×C4+0.149×C5

(14)

B2=0.473×C6+0.073×C7+0.170×C8+0.284×C9

(15)

B3=0.800×C10+0.200×C11

(16)

表1 各级指标对应判断矩阵与计算结果汇总Tab.1 Summary of correspondence judgment matrix and calculation results for indexes at all levels

表2 各级评价指标及其权重值Tab. 2 Evaluation indexes at all levels and their weight values

2 移动应用众包测试人员评价模型改进

直接使用上述模型仅能静态地评价众包人员在众包测试中的能力。要对测试人员进行全面客观的评价，使测试人员与测试任务更加匹配，还需要考虑企业对测试人员的具体要求以及测试人员自身的特征。故引入需求列表(Requirement List, RL)，其中RL={R0,R1,…,Ri,…,Rn}。将测试人员的身份特征、设备特征、任务偏好这三个描述特征引入描述表(Description list, DL)，DL={D0,D1,…,Di,…,Dn}。通过RL和DL构建n+1行n+1列的测试人员匹配矩阵(Tester Match Matrix, TMM)，其表达式为：

(17)

msii(i=0,1,…，n)表示第i项人员需求与第i项人员描述特征的匹配得分(match score, ms)。msii表达式如下：

msii=match(Ri,Di)； 0≤i≤n

(18)

式中:match表示人员需求与人员描述匹配函数，且match(Ri,Di)∈[0,1]。

测试人员匹配矩阵TMM是一个类单位矩阵，只有主对角线上取值为msii，其余元素均为0。将矩阵TMM的行列式值|TMM|作为n行人员需求与n列人员描述是否全部匹配的依据，若|TMM|=0，则未完全匹配，若|TMM|=1，则完全匹配。|TMM|计算方法如下：

(19)

通过将|TMM|与式(13)的结果A相乘作为移动应用众包测试人员评价模型的修正，修正后的模型A′的计算方法如式(20)所示:

A′=|TMM|×A

(20)

3 仿真与分析

通过构造模型并对其修正，得出最终的移动应用众包测试人员层次分析评价模型，为了验证该模型在实际评价过程中结果是否准确，需要验证准确性与单调性。准确性用模型评价结果与移动应用众包测试平台Testin中的测试人员的总体评分的误差衡量，误差越小，说明相关性越强。单调性表示模型评价结果能否准确预测总体评分的排序。本文采用皮尔逊相关性系数验证模型的准确性，采用斯皮尔曼等级相关系数验证模型的单调性，并对该模型的实际应用结果进行分析。

3.1 评价指标

1)皮尔逊相关性系数。

皮尔逊相关性系数又称皮尔逊积矩相关系数(Pearson Product-Moment Correlation Coefficient, PPMCC)、简单相关系数，它描述了两个定距变量间联系的紧密程度[16]，一般用r表示，计算公式为：

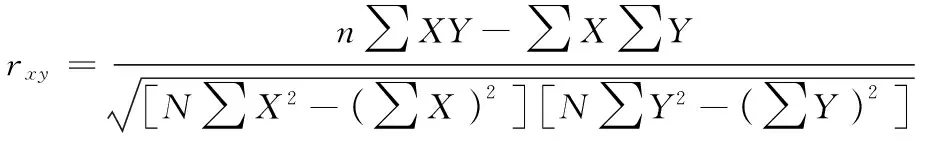
(21)

式中：N为样本量；X、Y为两个变量的观测值。若r>0，表明两变量正相关；若r<0，表明两变量负相关。r的绝对值越大表明两变量的相关性越强，一般定义为：1)0.6<|r|≤0.8，强相关；2)0.4<|r|≤0.6，中等程度相关；3)0.2<|r|≤0.4，弱相关；4)0.0≤|r|≤0.2，极弱相关或无相关。

2)斯皮尔曼等级相关系数。

斯皮尔曼等级相关系数(Spearman Rank Correlation, SROCC)是依据等级信息研究两变量之间相关关系的方法[17]。若样本的样本容量为n，则n个包含等级数据xi、yi的原始数据的斯皮尔曼等级相关系数ρ计算公式为：

ρ=1-6∑(xi-yi)/[n(n2-1)]

(22)

斯皮尔曼相关系数表明独立变量X和依赖变量Y的相关方向。当X增加，Y趋向于增加时，斯皮尔曼相关系数为正；当X增加，Y趋向于减少时，斯皮尔曼相关系数为负。当X增加、Y没有任何趋向性时，斯皮尔曼相关系数为0；当X和Y完全单调相关时，斯皮尔曼相关系数的绝对值为1。

3.2 实验过程

本文从Testin测试平台获取从2016年7月—12月的移动应用众包测试数据，为了保证数据的有效性，仅仅选取活跃用户作为实验数据来源，其中活跃用户1 798名，共完成众包任务9 865件。

从上述众测人员中随机选取100名众测人员作为实验评价对象，从Testin测试平台获取所选众包测试人员的测试申请、测试Bug发现、客户评价等历史数据，采用本文提出的评价模型，分别计算其二级评价指标，以及通过加权计算其一级指标和最终评价总分。最后基于改进模型，优化众测人员的最终评分。

本文通过计算原始模型评分、改进后的模型评分与网站评分之间的皮尔逊相关系数和皮尔斯曼等级相关系数来反映模型评分与网站评分之间的关联度，进而反映模型评价的有效性。

3.3 实验结果及分析

通过相关计算，一级指标个人活跃度、个人测试能力及个人诚信度的评分及经过本文提出的评价模型评分、改进后的模型评分与网站原有评分对比如表3所示。

表3 评价模型的数据示例Tab. 3 Data examples for the evaluation model

从表3可以看出，运用原始模型和改进后的模型进行人员评价，不仅能够计算出测试人员的能力总体评分，而且能够计算出模型的一级指标如个人活跃度、个人诚信度等的评分，在展现测试人员综合测试能力的同时，可以通过一级指标更加全面地评价众包测试人员，测试人员也能根据一级指标的评分在自身短板处有所提升。

使用Python语言对经预处理的数据进行计算，并使用Matlab根据所选样本数据的散点分布得出皮尔逊相关性系数(r(PPMCC))和斯皮尔曼等级相关系数(ρ(SROCC))，原始模型及对模型改进后的模型相关性系数曲线分别如图2所示。

图2 不同模型的相关性系数曲线Fig. 2 Correlation coefficient curves of different models

图2(a)中X代表原始模型评价结果，图2(b)中X代表改进后的模型评价结果，图2中Y均代表检验数据中的网站评分。经计算，原始模型与改进后模型对应的皮尔逊相关性系数、斯皮尔曼等级相关系数结果及显著性检验结果如表4所示。

表4中，原始模型及改进后的模型的皮尔逊相关性系数r(PPMCC)分别为0.990及0.992，均满足0.8

表4 相关性系数PPMCC和SROCC结果Tab. 4 Results of correlation coefficients for PPMCC and SROCC

通过皮尔逊相关性系数r(PPMCC)验证了原始模型评价结果、改进后的模型评价结果与原数据集中的移动应用众包测试人员总体执行评价数值相关性都较强，且改进后的模型评价结果更为准确。通过斯皮尔曼相关系数ρ(SROCC)证明原始模型及改进后的模型都能够较为准确地预测原数据集中评分的排序，表明移动应用众包测试人员层次分析评价模型较为有效。

由上述实验结果可知，本文所提出的模型及修改后的模型评分与该网站的评分在大多数情况下是极为相近的，且数据相近的情况大多出现在用户参与了大量的众包测试活动的情况下。虽然网站评分也存在较强的主观性，但对于参与测试次数多的用户，即使单次评价存在较大误差，出现正负误差的概率是相等的，在评价次数多的情况下正负误差抵消，总体误差值极小。故在目前缺乏对移动应用众包测试人员客观评价的基准方法的情况下，可通过计算模型评价结果与网站评分之间的相关性来验证模型评价结果的准确性，本文提出的评价模型在样本数据较多时是准确有效的。

虽然仍有部分经原始模型与改进后的模型评价得出的结果与Testin网站评分之间存在较大的偏差，但经分析后发现这些偏差主要出现在参与众包测试次数较少的众测人员身上。此类人员由于参加的众测次数较少，累计评价次数也少，数据的可置信度低，因此网站评分不具有客观性。且本文所提模型中的二级评价指标包含了月均参与任务数与参与任务总数这两项指标，表明该模型是综合考虑了众测人员参与测试次数这一因素的，是对网站评价的一种修正，结果更为客观，故当存在偏差时通过本文模型计算评分应比网站评分更为准确。

4 结语

本文运用层次分析法，结合移动应用众包测试的特征，提出移动应用众包测试人员层次分析评价模型。该模型的特点是：1)将移动应用测试的实际情况与专家的经验相结合，使得评价结果更加科学和客观。2)运用层次分析法时分析指标考虑较为全面，模型适用性强。3)引入需求列表与描述列表对本模型进行改进，测试人员与测试任务匹配度更高。通过运用皮尔逊相关性系数和斯皮尔曼等级相关系数对本文模型进行验证，结果表明了本文模型及改进后的模型的有效性和准确性。

本文所提出的移动应用众包测试人员层次分析评价模型可对测试人员作出准确评价，有助于任务发布者高效、准确地对测试人员进行筛选。在下一步的研究中，将进一步完善模型，引入更加全面的指标，以实现对移动应用众包测试人员层次分析评价模型更加精确的模拟。

References)

[1] HOWE J. Crowdsourcing: why the power of the crowd is driving the future of business [J]. Journal of Consumer Marketing, 2009, 26(4): 305-306

[2] MAO K, CAPRA L, HARMAN M, et al. A survey of the use of crowdsourcing in software engineering [J]. Journal of Systems and Software, 2016, 126(2017): 57-84.

[3] 张志强,逄居升,谢晓芹,等.众包质量控制策略及评估算法研究[J].计算机学报,2013,36(8):1636-1649.(ZHANG Z Q, PANG J S, XIE X Q, et al. Research on crowdsourcing quality control strategies and evaluation algorithm [J]. Chinese Journal of Computers, 2013, 36(8): 1636-1649.)

[4] AMBATI V, VOGEL S, CARBONELL J. Towards task recommendation in micro-task markets [C]// Proceedings of the 11th AAAI Conference on Human Computation. Menlo Park: AAAI, 2011: 80-83

[5] YUEN M C, KING I, LEUNG K S. Taskrec: probabilistic matrix factorization in task recommendation in crowdsourcing systems [C].//ICONIP 2012: Proceedings of the 2012 International Conference on Neural Information Processing, LNCS 7664. Berlin: Springer, 2012: 516-525.

[6] GEIGER D, SCHADER M. Personalized task recommendation in crowdsourcing information systems — current state of the art [J]. Decision Support Systems, 2014, 65(C): 3-16.

[7] HO C J, VAUGHAN J W. Online task assignment in crowdsourcing markets [C]// AAAI’12: Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence. Menlo Park: AAAI, 2012: 45-51.

[8] 李勇军,郭基凤,缑西梅.软件“众包”任务分配方法[J].计算机系统应用,2015,24(2):1-6.(LI Y J, GUO J F, GOU X M. Software task allocation method in crowdsourcing [J]. Computer Systems & Applications, 2015 ,24(2): 1-6.)

[9] 肖江辉.基于可信度的众包协同测试及其算法实现[D].大连:大连海事大学,2015:6.(XIAO J H. A research on trust-based crowdsourced collaborative testing and algorithm implementation [D]. Dalian: Dalian Maritime University, 2015:6.)

[10] WOODRUFF C K. Job performance evaluation of data processing personnel: an empirical study [J]. ACM SIGCPR Computer Personnel,1980, 8(4): 7-10.

[11] BOLTON D L. Evaluating Administrative Personnel in School Systems [M]. New York: Teachers College Press,1980: 29-32.

[12] 陈龙猛.基于Internet的高校实验技术人员工作评价系统开发[J].实验室研究与探索,2014,33(6):243-246,251.(CHEN L M. Development of the evaluation system based on the Internet for working performance of college lab technicians [J]. Research and Exploration in Laboratory, 2014, 33(6): 243-246, 251.)

[13] 杨振英,万秋一.军队人员信息安全素养评价指标体系构建研究[J].网络安全技术与应用,2013(2):67-70.(YANG Z Y, WAN Q Y. Research on the construction of information security literacy evaluation index system [J]. Network Security Technology & Application, 2013(2): 67-70.)

[14] 张晓冬.系统工程[M].北京:科学出版社,2010:142-160.(ZHANG X D. Systems Engineering [M]. Beijing: Science Press, 2010: 142-160.)[15] 邱奇志,周洁,张金保.基于形式概念分析和层次分析法的应急管理能力模糊综合评价法[J]. 计算机应用,2014,34(6):1819-1824.(QIU Q Z, ZHOU J, ZHANG J B. Fuzzy comprehensive evaluation method for emergency management capability based on formal concept analysis and analytic hierarchy process [J]. Journal of Computer Applications, 2014, 34(6): 1819-1824.)

[16] RODGERS J L, NICEWANDER W A. Thirteen ways to look at the correlation coefficient [J]. American Statistician, 1988, 42(1): 59-66.

[17] 张文耀.用斯皮尔曼系数衡量网络的度相关[D].合肥:中国科学技术大学,2016:4.(ZHANG W Y. Measuring mixing patterns in complex networks by Spearman rank correlation coefficient [D]. Hefei: University of Science and Technology of China, 2016:4.)

This work is partially supported by the Industrial Science and Technology Research Project of Shaanxi Province (2016GY- 100), the Aerospace Science and Technology Support Program (2014HTXGD), the Aerospace CAST-BISEE Fund (2015MC1001061).

LIUYing, born in 1996, M. S. candidate. Her research interests include mobile application testing, crowdsourcing testing.

ZHANGTao, born in 1976, Ph. D., associate professor. His research interests include software security, mobile application testing.

LIKun, born in 1993, M. S. candidate. His research interests include mobile application testing.

LINan, born in 1996, M. S. candidate. Her research interests include software security.

Evaluationmodelofmobileapplicationcrowdsourcingtesters

LIU Ying*, ZHANG Tao, LI Kun, LI Nan

(SchoolofSoftwareandMicroelectronics,NorthwesternPolytechnicalUniversity,Xi’anShaanxi710072,China)

Mobile application crowdsourcing testers are anonymous, non-contractual, which makes it difficult for task publishers to accurately evaluate the ability of crowdsourcing testers and quality of test results.To solve these problems, a new evaluation model of Analytic Hierarchy Process (AHP) for mobile application crowdsouring testers was proposed. The ability of crowdsourcing testers was evaluated comprehensively and hierarchically by using the multiple indexes, such as activity degree, test ability and integrity degree. The combination weight vector of each level index was calculated by constructing the judgment matrix and consistency test. Then, the proposed model was improved by introducing the requirement list and description list, which made testers and crowdsourcing tasks match better. The experimental results show that the proposed model can evaluate the ability of testers accurately, support the selection and recommendation of crowdsourcing testers based on the evaluation results, and improve the efficiency and quality of mobile application crowdsourcing testing.

mobile application crowdsourcing testing; personnel evaluation; Analytic Hierarchy Process (AHP); Pearson correlation coefficient; Spearman correlation coefficient

2016- 05- 20;

2017- 07- 24。

陕西省工业科技攻关项目(2016GY- 100)；航天科技支撑计划项目(2014HTXGD)；航天CAST-BISEE基金资助项目(2015MC1001061)。

刘莹(1996—)，女，四川绵阳人，硕士研究生，主要研究方向：移动应用测试、众包测试； 张涛(1976—)，男，陕西宝鸡人，副教授，博士，主要研究方向：软件安全、移动应用测试； 李坤(1993—)，男，陕西西安人，硕士研究生，主要研究方向：移动应用测试;李楠(1996—)，女，陕西商洛人，硕士研究生，主要研究方向：软件安全。

1001- 9081(2017)12- 3569- 05

10.11772/j.issn.1001- 9081.2017.12.3569

(*通信作者电子邮箱894749065@qq.com)

TP301.4

A