Stability Analysis for Memristive Recurrent Neural Network and Its Application to Associative Memory

Gang Bao Yuanyuan Chen Siyu Wen Zhicen Lai

Stability Analysis for Memristive Recurrent Neural Network and Its Application to Associative Memory

Gang Bao1Yuanyuan Chen1Siyu Wen1Zhicen Lai1

Memristor is a nonlinear resistor with variable resistance.This paper discusses dynamic properties of memristor and recurrent neural network(RNN)with memristors as connection weights.Firstly,it establishes that there exists a threshold voltage for memristor.Secondly,it presents a model for memristive recurrent neural network(MRNN)which has variable and bounded coeきcients,and analyzes stability of memristive neural network by some maths tools.Thirdly,it gives a synthesis algorithm for associative memory based on memristive recurrent neural network.At last,three examples verify our results.

Associative memory,memristor,memristive recurrent neural network(MRNN),stability

1 Introduction

Arti fi cial neural networks are developed for solving some complex problems in control,optimal computation,pattern recognition,information processing,and associative memory[1]−[13].American scientist Hop fi eld makes a great contribution for the development of neural network.That is the implementation of neural network by simple circuit devices,resistors,capacitors and ampli fi ers[14].Hop fi eld neural network(HNN)can mimic the human’s associative memory function and accomplish optimization.The key point is the weights of HNN which are implemented by resistors for simulating neuron synapse.While the bottleneck is that linear resistors cannot re fl ect variability of synapse for resistance of linear resistor being invariable.

Memristor[15],[16],the arising fourth circuit device,makes it better to simulate the variability of neuron synapse.Pershin and Ventra[17]gives their experimental research results that neurons with memristors as synapses can simulate the associative memory function of a dog.Hence,memristor is the advancing spot in the present physics research.Several models of memristor have been set up and its properties have been analyzed in[18]−[21].Based on these analyses,memristor can be used to mimic synapse in neural computing architecture[22],construct memristor bridge synapse[23]and brain combined with the conventional complementary metal oxide semiconductor(CMOS)technology[24],set memristive neural network[25],[26]and implement memristor array for image processing[27]etc.

Some researchers derive mathematical model of memristive recurrent neural network(MRNN)by replacing resistors with memristors in Hop fi eld and cellular neural network circuit[28]−[30].MRNN is modeled by statedependent switched systems by simplifying the memristance as two-valued device with diあerent terminal voltage.With diあerential inclusion theory,Lyapunov-Krasovskii function and some other math tools,some suきcient conditions are derived for dynamics of MRNN,such as,convergence and attractivity[31]−[33],periodicity and dissipativity[34],dissipativity for stochastic and discrete case,global exponential almost periodicity,and complete stability[35],multi-stability[36],etc.Considering the trouble from the switching property of memristor,researchers derive some interesting results about exponential stabilization,reliable stabilization,and fi nite-time stabilization of MRNN by designing diあerent state feedback controllers[37],[38]and sampled-data controller[39]. All of these results make a solid foundation for MRNN’s application to associative memory.

Associative memory is a distinguished function of human brain which can be simulated by recurrent neural network(RNN).The design problem is that some given prototype patterns are to be stored by RNN,and then the stored patterns can be recalled by some prompt information.In the existing literatures[40]−[46],there are two design methods for associative memory.One is that prototype patterns are designed as multiple locally asymptotically stable equilibria and initial values are the recalling probes.Another is that a prototype pattern is designed as the unique globally asymptotically stable equilibrium point with one external input as the recalling probe.Diあerent external inputs mean different equilibrium points,i.e.,diあerent prototype patterns.

To the best of our knowledge,the bottleneck of associative memory based on RNN is that capacity of RNN is limited and diあerent storage task needs diあerent RNN because resistance can not be changed.Furthermore,there are few works about associative memory based on MRNN.Hence,the contribution of this paper is obtaining a threshold voltage for memristor by simulation,presenting a novel type of MRNN with in fi nite number of sub neural networks,and design a program for associative memory based on MRNN.Compared with MRNN models in the existing literatures,the diあerence is that every coeきcient of MRNN has in finite number of values,not two values.Furthermore,every coeきcient can be changed by the external input.So the associative memory based on MRNN seems to solve the problem of storage capacity.

The rest of this paper is organized as the following sections.Memristor property analysis and some preliminaries are stated in Section 2.Then,some suきcient conditions are given to ensure global stability and multi-stability of MRNN by some maths tools in Section 3,respectively.Next,design procedure for associative memory based on MRNN is given in Section 4.To elucidate our results,three simulation examples are presented in Section 5.At last,conclusion is drawn in Section 6.

2 Memristor Recurrent Neural Network Model

2.1 Memristor and Its Property

The de fi nition of memristor[15]is a functional relation between chargeqand magnetic fl uxφ,i.e.,g(φ,q)=0.Memristance of memristor is de fi ned as the following formula with the assumption of linear dopant drift as follows wherew(t),D,i(t),v(t),µVare the length of dopant region,the length of memristor,the current,voltage across the device and the average ion mobility,respectively.

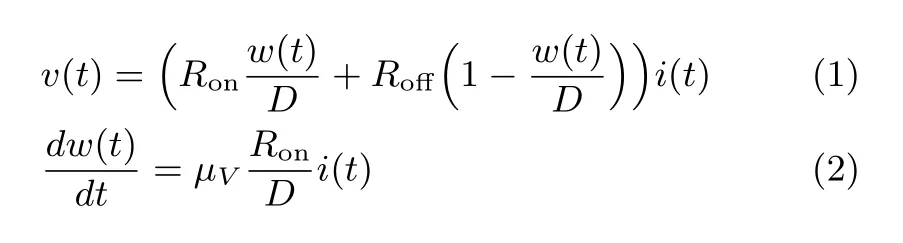
Thev-isimulation curve of memristor(1)with MATLAB is shown in Fig.1.

Fig.1.The curve of(v(t),i(t))under voltage sources with diあerent amplitudes.The applied voltage source is v(t)=v0sin(ωt),v0=1.5,1,0.15,0.01V,ω=2π rad/s and the other parameters ares(t0)=0.1,t0=0 s,Ron=100Ω,r=160,D=10−6cm,µV=10−10cm2/sV.From four subplots,there is a threshold voltage existing for one memristor.

From Fig.1,it shows that a memristor will not change its resistance unless the terminal voltage exceeds a certain threshold valueVTas described in[20],[27].It can be expressed by the following formula

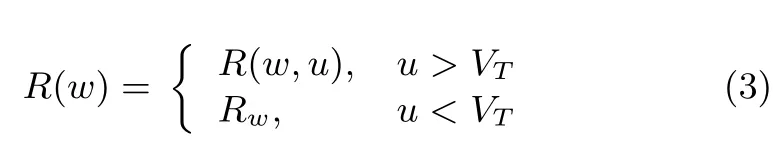
whereRwis a constant betweenRonandRoあ;R(w,u)can be calculated by the following formula[10]

where ΦD=(rD)2/[2µv(r−1)];VA,Tw,andR(w0),R(w)are voltage amplitude,time width,resistances of the device at the statesw0,w,respectively.

Remark 1:Simulation shows that there exists a threshold voltage for the memristor,i.e.,memristance can be changed by terminal voltage with amplitude value being greater than threshold value.The result is consistent with the theoretical analysis in[20].This property of memristor can re fl ect variability of neuron synapses.Furthermore,it makes memristor being suitable for constructing neural network with coeきcients which can be changed according to our needs.

2.2 Model

In this section,we will fi rstly present the mathematical model for MRNN,and then give some concepts and lemmas in order to obtain our main results.MRNN is modelled by the following diあerential equation systems:

where i=1,2,...,n,x(t)=(x1(t),...,xn(t))T∈Rnis the state vector;A(ui)=(aij(ui)),B(ui)=(bij(ui))and C=diag{c1,c2,...,cn}are connection weight matrices;aij,bijare related to external inputs u=(u1,...,un)T∈Rn;ci＞0,i=1,2,...,n,∀t≥t0,∀i,j∈{1,2,...,n},0＜ τ(t)≤ τ is the time-varying delay;f is a bounded activation function satisfying the following condition

wherer1,r2,µ∈R andµ＞0.

According to circuit theory and the property of memristor,it results that there exist some constantssuch that

Remark 2:Compared with these models in[31]−[38],the diあerence of MRNN(5)is that coeきcientsaij(ui)andbij(ui),i,j=1,2,...,nare continuous variable functions with respect to external inputsui.Memristor has multi resistances as demonstrated by real device experiments and circuit simulation in[47].Hence,MRNN can be seen as a neural network with an in fi nite number of modes becauseaij(ui),bij(ui)belong to intervalsandrespectively.While the existing results are 2n2+1sub modes in[31],[32].So MRNN(5)seems to model human neurons network more better.

2.3 Preliminaries

Letu=(u1,u2,...,un)be the external input and denotex(t;t0,φ,u)as the state of MRNN(5)with someuand initial value,

whereφ(ϑ)∈C([t0−τ,t0],D),D∈Rn.Then,x(t;t0,φ,u)is continuous and satis fi es MRNN(5)andx(s;t0,φ,u)=φ(s),fors∈[t0−τ,t0].For simplicity,letx(t)be the state of MRNN(5).

De fi nition 1[48]:The equilibrium pointx?of MRNN(5)is said to be locally exponentially stable in regionD,if there exist constantsα＞0,β＞0 such that∀t≥t0

wherex(t;t0,φ,u)is the solution of MRNN(5)with any external inputuand initial conditionφ(ϑ)∈C([t0−τ,t0],D).Dis said to be a locally exponentially attractive set of the equilibrium pointx∗.WhenD=Rn,x∗is said to be globally exponentially stable.

Lemma 1[49]:LetDbe a bounded and closed set in Rn,andHbe a mapping on complete metric space(D,||·||),where∀x,y∈D,||x−y||=max1≤i≤n{|xi−yi|}is measurement inD.IfH(D)⊂Dand there exists a constantα＜1 such that∀x,y∈D,||H(x)−H(y)||≤α||x−y||,then there exists a uniquex∗∈Dsuch thatH(x∗)=x∗.

3 Stability Analysis for MRNN

Stability of MRNN is the foundation for its application to associative memory.So we discuss global stability and multi-stability of MRNN in the following subsections.Firstly,we analyze the diあerences between MRNN and traditional RNN.Traditional RNN is described by,fori,j=1,2,...,n,

whereci,aij,bij,uihave the same means as those in(5).

Discussion:According to above analysis,coeきcientsaij(ui),bij(ui)of MRNN(5)can take any values inWhile the corresponding coeきcients of RNN cannot be changed.So MRNN(5)is a family of neural networks with in fi nitely many modes or sub neural networks.Hence MRNN may have in fi nite number of globally or locally stable equilibrium points.Coeきciens of the interval RNN[50]may be constants in diあerent intervals because coeきcients increments△aij,△bijare caused by noises and implementation errors.This is diあerent from MRNN but the systematic analysis method[50]can be as a reference for stability analysis of MRNN.

3.1 Global Stability Analysis

This subsection discusses global stability of MRNN(5).By using comparative principle and the existing stability criteria,it derives some suきcient conditions for global stability of(5).The following activation function will be adopted in the rest of the paper

Obviously,|f(r1)−f(r2)|≤|r1−r2|,r1,r2∈R.In order to derive our result,the following lemma is needed.

Lemma 2:If the following three diあerential systems

have one common equilibrium pointy?=0,g1(0)=g2(0)=g3(0)=0 and satisfyingg1(y)≤g2(y)≤g3(y),then system(11)is globally exponentially stable if systems(10)and(12)are globally exponentially stable.

Proof:Take the same initial valuey(t0)=0 for three systems,lety?1,y?2denote equilibrium points of(10)and(12),respectively.Then

Hence,|y1(t)|≤|y2(t)|≤|y3(t)|or|y3(t)|≤|y2(t)|≤|y3(t)|.And(10)and(11)are globally exponentially stable,there existα1,α3,β1,β3,initial valuesφ1,φ3satisfying

So there must existα2,β2and an initial valueφ2,and the following inequality

is valid,i.e.,(11)is globally exponentially stable. ■

Because the external inputsui,i=1,2,...,nare just used to change the memristance,we assume that all of sub neural networks have the same external inputsui,i=1,2,...,nin the following discussion.

Lemma 3[48]:If forci,aijandbij,∀i,j∈{1,2,...,n},C−|A|−|B|is a nonsingularMmatrix with|A|=(|µjaij|)n×nand|B|=(|ωjbij|)n×n,µj,ωjare positive constants forj=1,2,...,n,then the corresponding equilibrium point of(14)is globally exponentially stable.

By(5)and(7),we haveNN1

andNN2

fori=1,2,...,n.

Theorem 1:If coeきcients of neural networks(14)and(15)satisfy thatC−|A|−|B|is a nonsingularMmatrix with|A|=(|aij|)n×nand|B|=(|bij|)n×n,then(5)is globally exponentially stable forand bounded external inputsui,i,j=1,2,...,n.

Proof:Because the activationf(r)satisfy the Lipschitz condition andui,i=1,2,...,nare bounded,there must exist one equilibrium for(5)at least by the Schauder fi xed point theorem forand bounded external inputsui,i,j=1,2,...,n.Denoteequilibrium points of(5),(14),(15),respectively.

Let

Let

Since

then

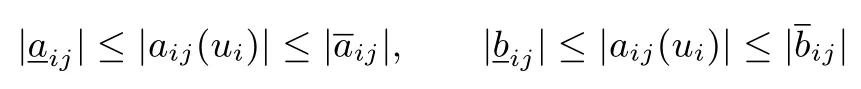
or

So

or

According to the condition of Theorem 1,(17),(19),(20)and Lemma 3,there must exist positive constantsαandβsatisfying|Vi(t)|≤αexp{−βt}.Hence the conclusion of this theorem is valid. ■

Remark 3:Whenfori,j=1,2,...,n,the result in[48]can be obtained from Theorem 1.So we generalize the result of[47]to discuss global stability of MRNN(5)with in fi nite number of sub neural networks.Compared with the existing literatures,its main merit is that MRNN(5)has many globally exponentially stable equilibrium points.The systematic method in[43]can be used to derive suきcient conditions for global stability of(5)by virtue of many global stability criteria in the existing literatures.

医院进一步科普规范化，对队员进行徒手心肺复苏术，创伤、突发事件、突发疾病时的紧急救护技术等统一培训，定期考核，确保培训水平同质化。

3.2 Multi-stability of MRNN

Multi-stability of RNN means that RNN has coexisting multi attractors.Memory patterns can be stored by these attractors.Memory capacity of RNN is up to the number of attractors.Another factor aあecting memory is the activation functionf(r).Zenget al.has derived some suffi cient conditions for multi-stability ofndimensional RNN with the activation functionf(r)=(|r+1|−|r−1|)/2 which has 3nequilibrium points and 2nequilibrium points of them are locally exponentially stable.And then Zenget al.[49]generalize their work tondimensional RNN with the activation function(9).They derive that RNN with the activnation function(9)has(4k−1)nequilibrium points and(2k)equilibrium points of them are locally exponentiallystable in where

But there are limited number of equilibrium points and output patterns for RNN with these two kinds of activation functions.Hence,we discuss multi-stability of MRNN with the activation function(9).

Lemma 4[49]:For the given integerk≥1,if∀i,j∈{1,2,...,n},the following inequalities are valid for coeき-cientsci,aij,bijand external inputsuiof RNN with the activation function(9)

then RNN with the activation function(9)has(4k−1)nequilibrium points and(2k)nof them are locally exponentially stable.

Theorem 2:If the following inequalities are valid

then forci,aijandbij∀i,j∈{1,2,...,n},the corresponding MRNN(5)has(4k−1)nequilibria located in Ωk,(2k)nof them are locally exponentially stable.

Proof:In order to prove multi-stability of(5),it is suffi cient to verify whether conditions(22)and(23)are valid or not.Forwe have

And then

Hence,(22)and(23)are valid forci,aij(ui),bij(ui),i,j=1,2,...,n.By Lemma 4,the conclusion of Theorem 2 is valid. ■

Remark 4:In fact,(24)and(25)are minimum value and maximum value of(22)and(23),respectively.Hence,we generalize the systematic method[50],[51]to analyzing multi-stability of MRNN.Compared with results in[49],the conditions are more conservative.But MRNN has in finite number of sub neural networks,i.e,globally exponentially stable equilibrium points of MRNN(5)are in fi nite times(2k)n.By virtue of the existing results for multistability of RNN,we can obtain many suきcient conditions for multi-stability of MRNN(5).

4 Associative Memory Synthesis

Based on the above analysis,we discuss associative memory design method based on MRNN(5).Memory patterns are described by bipolar value{−1,1}.Associative memory is implemented by RNN circuit.So the activation function is taken asf(r)=(|r+1|−|r−1|)/2,r∈R and weight values are simulated by linear resistors.So associative memory can just remember bitmap,and storage capacity is limited.So our associative memory synthesis is based on MRNN with(9).It is able to memorize gray map and has in fi nite storage capacity.The key point of associative memory synthesis is the computation for weights value.So we fi rstly describe the synthesis problem,and then present our design method based on Zeng and Wang’s work[43].The activation functionF(r)=0,r＜0,F(r)=f(r),r＞0 wheref(r)is de fi ned as(9).The purpose is to make the designed neural network be able to memorize gray map.

Synthesis Problem:There arepmemory patterns being denoted by vectorsα1,α2,...,αp,αi∈{0,1,3,5,...,4k−3}n,i=1,2,...,p.Compute coeきcientsci,aij,bijanduiin order thatα1,α2,...,αp,αiare stable memory vectors of MRNN(9).

Design procedure:

Step1:Use vectorsα1,α2,...,αp,αi∈{0,1,3,5,...,4k−3}n(n,the dimension of MRNN)presenting the desired memory pattern.Ifp≤(2k)n,then go to Step 2 computing coeきcientsci,aij,bijandui.Ifp=q(2k)n+γ,then divideα1,α2,...,αpintoq+1 groups.Go to Step 2 and compute coeきcients for each group.

Step 2:For the desired memory vectors,do the following:

2)Takeσi＞1,i=1,2,...,nand chooseaij,bijsatisfyingaii+bii−σi=tiiandaij+bij=tij;wherel,S(l)are de fi ned in[41].

Step 3:Ifp=(2k)n,compute memristanceMijaccording toaij,bij;ifp=q(2k)n+γ,compute memristanceMijaccording to|aij|max,|bij|maxwhere

Remark 5:Compared with the work in[41],we do not require thatp,the number of desired memory vectors,is less than or equal to(2k)n.Hence,we generalize Zeng and Wang’s work[43].And we choose the activation function(9)in order to make the designed associative memory MRNN be able to memorize gray map not bitmap.This is one diあerence from the existing work.Another merit is that the designed MRNN has in fi nite number of equilibrium points,i.e.,MRNN can be used to implement large storage capacity associative memory.For example,RNN withf(r)=(|r+1|−|r−1|)only has 2nmemory patterns in{−1,1}nand RNN with(9)only has(4)nmemory patterns in{−5,−1,1,5}nwhenk=2.MRNN breaks this bottleneck for it has variable coeきcients and in fi nite memory patterns.

5 Illustrative Examples

Example 1:Consider the following MRNN with activation functionf(r),r∈R(9)withk=1,n=2.

where

Fig.2.Transient behaviors of x1(t)of MRNN(26).

Fig.3.Transient behaviors of x2(t)of MRNN(26).

According to Theorem 1,every sub neural network of MRNN(26)is globally exponentially stable.Leta11=a22=−3,a12=a21=1/2,b11=b22=1,b12=1/4,b21=1/2,and simulate with 50 initial values.The dynamic characteristics are shown in Figs.2−4.

Fig.4.Phase plot of x1(t)and x2(t)of MRNN(26).

Example 2:Consider a MRNN with activation functionf(r),r∈R(9)withk=2,n=2.

where

According to Theorem 2,every sub neural network of MRNN(26)has 72isolated equilibrium points and 42of them are locally exponentially stable.Take maximum values foraij,bij,i,j=1,2 and simulate with 50 initial values.The dynamics characteristics are shown in Fig.5.

Example3:The same example has been introduced by Lu and Liu[52],Zeng and Wang[43]for associative memory synthesis.The desired memory patterns are three letters“I,L,U” and number“7” as plotted by gray Fig.6.

These four desired patterns can be denoted by memory vectors

Fig.5.Transient behaviors of x1(t)and x2(t)of MRNN(27).

Fig.6. Three letters“I,L,U” and number“7” being presented by gray map.

The objective is to design one 12 dimension MRNN withα1,α2,α3,α4being stable memory vectors. Obviously,the number of stable memory vectors is less than(2k)n(k=2,n=12).Forl=12,then we add eights vectorsα5,...,α8such that is an invertible matrix.Chooseui=1.825(external inputs),i=1,2,...,12,λli=1.5(i=1,2,...,12;l=1,2,3,4),l=5,6,...,12).The function ofis to make these memory vectors be in the stable region Ωk.According to associative memory synthesis program,we can obtain

whereW=(tij),tij=aij+bij.It is easy to verify thatα1,α2,α3,α4are stable memory vectors according to Theorem 2.Takeci=1,i=1,2,...,n,aij=bij,ui=0.425,then we have the MRNN with these desired patterns as stable memory vectors.

6 Concluding Remarks

In this paper,we have introduced MRNN which is a family of recurrent neural networks.Some suきcient conditions are derived to assure its mono-stability and multi-stability.In the existing literature on neural network,the largest number of equilibrium points is(4k−1)nand(2k)nof them are locally exponentially stable.In fact,associative memory output patterns are up to the activation function.This point aあects the storage capacity of associative memory.Our MRNN with coeきcients in intervals cannot be limited by output value of the activation.Hence MRNN can increase the storage capacity of associative memory.This is the main merit which is diあerent from traditional arti fi cial neural network.So self-adaptive and self-organization recurrent neural network can be realized with memristor[26]in the future.

1 T.Mareda,L.Gaudard,and F.Romerio,“A parametric genetic algorithm approach to assess complementary options of large scale windsolar coupling,”IEEE/CAA J.Autom.Sinica,vol.4,no.2,pp.260−272,Apr.2017.

2 Y.Zhao,Y.Li,F.Y.Zhou,Z.K.Zhou,and Y.Q.Chen,“An iterative learning approach to identify fractional order KiBaM model,”IEEE/CAA J.Autom.Sinica,vol.4,no.2,pp.322−331,Apr.2017.

3 L.Li,Y.L.Lin,N.N.Zheng,and F.Y.Wang,“Parallel learning:a perspective and a framework,”IEEE/CAA J.Autom.Sinica,vol.4,no.3,pp.389−395,Jul.2017.

4 M.Yue,L.J.Wang,and T.Ma,“Neural network based terminal sliding mode control for WMRs aあected by an augmented ground friction with slippage eあect,”IEEE/CAA J.Autom.Sinica,vol.4,no.3,pp.498−506,Jul.2017.

5 W.Y.Zhang,H.G.Zhang,J.H.Liu,K.Li,D.S.Yang,and H.Tian,“Weather prediction with multiclass support vector machines in the fault detection of photovoltaic system,”IEEE/CAA J.Autom.Sinica,vol.4,no.3,pp.520−525,Jul.2017.

6 D.Shen and Y.Xu,“Iterativelearning controlfor discrete-time stochastic systems with quantized information,”IEEE/CAA J.Autom.Sinica,vol.3,no.1,pp.59−67,Jan.2016.

7 Z.Y.Guo,S.F.Yang,and J.Wang,“Global synchronization of stochastically disturbed memristive neurodynamics via discontinuous control laws,”IEEE/CAA J.Autom.Sinica,vol.3,no.2,pp.121−131,Apr.2016.

8 X.W.Feng,X.Y.Kong,and H.G.Ma,“Coupled crosscorrelation neural network algorithm for principal singular triplet extraction of a cross-covariance matrix,”IEEE/CAA J.Autom.Sinica,vol.3,no.2,pp.147−156,Apr.2016.

9 S.M.Chen,X.L.Chen,Z.K.Pei,X.X.Zhang,and H.J.Fang,“Distributed fi ltering algorithm based on tunable weights under untrustworthy dynamics,”IEEE/CAA J.Autom.Sinica,vol.3,no.2,pp.225−232,Apr.2016.

10 L.Li,Y.S.Lv,and F.Y.Wang,“Traきc signal timing via deep reinforcement learning,”IEEE/CAA J.Autom.Sinica,vol.3,no.3,pp.247−254,Jul.2016.

11 F.Y.Wang,X.Wang,L.X.Li,and L.Li,“Steps toward parallel intelligence,”IEEE/CAA J.Autom.Sinica,vol.3,no.4,pp.345−348,Oct.2016.

12 T.Giitsidis and G.Ch.Sirakoulis,“Modeling passengers boarding in aircraft using cellular automata,”IEEE/CAA J.Autom.Sinica,vol.3,no.4,pp.365−384,Oct.2016.

13 B.B.Alagoz,“A note on robust stability analysis of fractional order interval systems by minimum argument vertex and edge polynomials,”IEEE/CAA J.Autom.Sinica,vol.3,no.4,pp.411−421,Oct.2016.

14 J.J.Hop fi eld,“Neural networks and physical systems with emergent collective computational abilities,”Proc.Natl.Acad.Sci.USA,vol.79,no.8,pp.2554−2558,Apr.1982.

15 L.Chua, “Memristor-the missing circuit element,”IEEE Trans.Circuit Theory,vol.18,no.5,pp.507−519,Sep.1971.

16 D.B.Strukov,G.S.Snider,D.R.Stewart,and R.S.Williams,“The missing memristor found,”Nature,vol.453,no.7191,pp.80−83,May 2008.

17 Y.V.Pershin and M.Di Ventra,“Experimental demonstration of associative memory with memristive neural networks,”Neural Netw.,vol.23,no.7,pp.881−886,Sep.2010.

18 F.Corinto,A.Ascoli,and M.Gilli,“Nonlinear dynamics of memristor oscillators,”IEEE Trans.Circuits Syst.I:Reg.Pap.,vol.58,no.6,pp.1323−1336,Jun.2011.

19 O.Kavehei,A.Iqbal,Y.S.Kim,K.Eshraghiam,S.F.Al-Sarawi,and D.Abbott,“The fourth element:characteristics,modelling and electromagnetic theory of the memristor,”Proc.Roy.Soc.A-Math.Phy.Eng.Sci.,vol.466,no.2120,pp.2175−2202,Mar.2010.

20 Y.Ho,G.M.Huang,and P.Li,“Dynamical properties and design analysis for nonvolatile memristor memories,”IEEE Trans.Circuits Syst.I:Reg.Pap.,vol.58,no.4,pp.724−736,Apr.2011.

21 L.Chua, “Resistance switching memories are memristors,”Appl.Phys.A,vol.102,no.4,pp.765−783,Mar.2011.

22 G.Snider,“Memristors as synapses in a neural computing architecture,”inMemristor and Memristor Syst.Symp.,Berkeley,CA,Nov.2008.

23 H.Kim,M.P.Sah,C.J.Yang,T.Roska,and L.O.Chua,“Neural synaptic weighting with a pulse-based memristor circuit,”IEEE Trans.Circuits Syst.I:Reg.Pap.,vol.59,no.1,pp.148−158,Jan.2012.

24 M.P.Sah,H.Kim,and L.O.Chua,“Brains are made of memristors,”IEEE Circuits Syst.Mag.,vol.14,no.1,pp.12−36,Feb.2014.

25 F.Z.Wang,N.Helian,S.N.Wu,X.Yang,Y.K.Guo,G.Lim,and M.M.Rashid,“Delayed switching applied to memristor neural networks,”J.Appl.Phys.,vol.111,no.7,Article ID,07E317,Apr.2012.

26 K.D.Cantley,A.Subramaniam,H.J.Stiegler,R.A.Chapman,and E.M.Vogel,“Neural learning circuits utilizing nano-crystalline silicon transistors and memristors,”IEEE Trans.Neural Netw.Learn.Syst.,vol.23,no.4,pp.565−573,Apr.2012.

27 X.F.Hu,S.K.Duan,L.D.Wang,and X.F.Liao,“Memristive crossbar array with applications in image processing,”Sci.China Inform.Sci.,vol.55,no.2,pp.461−472,2012.

28 M.Itoh and L.Chua,“Memristor cellular automata and memristor discrete-time cellular neural networks,”Int.J.Bifurcation Chaos,vol.19,no.11,pp.3605−3656,Mar.2009.

29 S.P.Wen,Z.G.Zeng,and T.W.Huang,“Associative learning of integrate-and- fi re neurons with memristor-based synapses,”Neural Proc.Lett.,vol.38,no.1,pp.69−80,Aug.2013.

30 A.L.Wu,S.P.Wen,and Z.G.Zeng,“Synchronization control of a class of memristor-based recurrent neural networks,”Inf.Sci.,vol.183,no.1,pp.106−116,Jan.2012.

31 S.T.Qin,J.Wang,and X.P.Xue,“Convergence and attractivity of memristor-based cellular neural networks with time delays,”Neural Netw.,vol.63,pp.223−233,Mar.2015.

32 Z.Y.Guo,J.Wang,and Z.Yan,“Attractivity analysis of memristor-based cellular neural networks with time-varying delays,”IEEE Trans.Neural Netw.Learn.Syst.,vol.25,no.4,pp.704−717,Apr.2014.

33 S.P.Wen,T.W.Huang,Z.G.Zeng,Y.R.Chen,and P.Li,“Circuit design and exponential stabilization of memristive neural networks,”Neural Netw.,vol.63,pp.48−56,Mar.2015.

34 G.D.Zhang,Y.Shen,Q.Yin,and J.W.Sun,“Global exponential periodicity and stability of a class of memristorbased recurrent neural networks with multiple delays,”Inf.Sci.,vol.232,pp.386−396,May 2013.

35 Z.Y.Guo,J.Wang,and Z.Yan,“Global exponential dissipativity and stabilization of memristor-based recurrent neural networks with time-varying delays,”Neural Netw.,vol.48,pp.158−172,Dec.2013.

36 X.B.Nie,W.X.Zheng,and J.D.Cao,“Coexistence and localµ-stability of multiple equilibrium points for memristive neural networks with nonmonotonic piecewise linear activation functions and unbounded time-varying delays,”Neural Netw.,vol.84,pp.172−180,Dec.2016.

37 S.B.Ding,Z.S.Wang,and H.G.Zhang,“Dissipativity analysis for stochastic memristive neural networks with time-varying delays:a discrete-time case,”IEEE Trans.Neural Netw.Learn.Syst.,pp.(99): 1−13,2016,doi:10.1109/TNNLS.2016.2631624.

38 A.L.Wu,Z.G.Zeng,X.S.Zhu,and J.E.Zhang,“Exponential synchronization of memristor-based recurrent neural networks with time delays,”Neurocomputing,vol.74,no.17,pp.3043−3050,2011.

39 S.B.Ding,Z.S.Wang,N.N.Rong,and H.G.Zhang,“Exponential stabilization of memristive neural networks via saturating sampled-data control,”IEEE Trans.Cybern.,vol.47,no,10,pp.3027−3039,Jun.2017.

40 A.N.Michel and D.L.Gray,“Analysis and synthesis of neural networks with lower block triangular interconnecting structure,”IEEE Trans.Circuits Syst.,vol.37,no.10,pp.1267−1283,Oct.1990.

41 G.Yen and A.N.Michel,“A learning and forgetting algorithm in associative memories:the eigenstructure method,”IEEE Trans.Circuits Syst.II:Anal.Digit.Signal Proc.,vol.39,no.4,pp.212−225,Apr.1992.

42 G.Seiler,A.J.Schuler,and J.A.Nossek,“Design of robust cellular neural networks,”IEEE Trans.Circuits Syst.I:Fundam.Theory Appl.,vol.40,no.5,pp.358−364,May 1993.

43 Z.G.Zeng and J.Wang,“Analysis and design of associative memories based on recurrent neural networks with linear saturation activation functions and time-varying delays,”Neural Comput.,vol.19,no.8,pp.2149−2182,Aug.2007.

44 M.Brucoli,L.Carnimeo,and G.Grassi,“Discrete-time cellular neural networks for associative memories with learning and forgetting capabilities,”IEEE Trans.Circuits Syst.I:Fundam.Theory Appl.,vol.42,no.7,pp.396−399,Jul.1995.

45 A.C.B.Delbem,L.G.Correa,and L.Zhao,“Design of associative memories using cellular neural networks,”Neurocomputing,vol.72,no.10−12,pp.2180−2188,Jan.2009.

46 G.Grassi,“On discrete-time cellular neural networks for associative memories,”IEEE Trans.Circuits Syst.I:Fundam.Theory Appl.,vol.48,no.1,pp.107−111,Jan.2001.

47 A.Ascoli,R.Tetzlaあ,L.O.Chua,J.P.Strachan,and R.S.Williams,“History erase eあect in a non-volatile memristor,”IEEE Trans.Circuits Syst.I:Reg.Pap.,vol.63,no.3,pp.389−400,Mar.2016.

48 Z.Y.Guo,J.Wang,and Z.Yan,“A systematic method for analyzing robust stability of interval neural networks with time-delays based on stability criteria,”Neural Netw.,vol.54,pp.112−122,Jun.2014.

49 Z.G.Zeng,J.Wang,and X.X.Liao,“Global exponential stability of a general class of recurrent neural networks with time-varying delays,”IEEE Trans.Circuits Syst.I:Fundam.Theory Appl.,vol.50,no.10,pp.1353−1358,Oct.2003.

50 Z.G.Zeng,T.W.Huang,and W.X.Zheng,“Multistability of recurrent neural networks with time-varying delays and the piecewise linear activation function,”IEEE Trans.Neural Netw.,vol.21,no.8,pp.1371−1377,Aug.2010.

51 Z.G.Zeng,J.Wang,and X.X.Liao,“Stability analysis of delayed cellular neural networks described using cloning templates,”IEEE Trans.Circuits Syst.I:Reg.Pap.,vol.51,no.11,pp.2313−2324,Nov.2004.

52 Z.J.Lu and D.R.Liu,“A new synthesis procedure for a class of cellular neural networks with space-invariant cloning template,”IEEE Trans.Circuits Syst.II:Anal.Digit.Signal Proc.,vol.45,no.12,pp.1601−1605,Dec.1998.

Gang Bao,Yuanyuan Chen,Siyu Wen,Zhicen Lai.Stability analysis for memristive recurrent neural network and its application to associative memory.Acta Automatica Sinica,2017,43(12):2244−2252

DOI10.16383/j.aas.2017.e170103

May 24,2017;accepted October 12,2017

This work was supported by the National Natural Science Foundation of China(61125303),the Program for Science and Technology in Wuhan,China(2014010101010004),the Program for Changjiang Scholars and Innovative Research Team in University of China(IRT1245),China Three Gorges University Science Foundation(KJ2013B020),Hubei Key Laboratory of Cascaded Hydropower Stations Operation and Control Program(2013KJX12),and Hubei Science and Technology Support Program(2015BAA106)

Recommended by Associate Editor Zhanshan Wang

1.Hubei Key Laboratory of Cascaded Hydropower Stations Operation and Control,School of Electrical Engineering and New Energies,China Three Gorges University,Yichang 443002,China

Gang Bao received the B.S.degree in mathematics from Hubei Normal University,Huangshi,China,the M.S.degree in applied mathematics from Beijing University of Technology,Beijing,China,in 2000 and 2004,the Ph.D.degree from the Department of Control Science and Engineering,Huazhong University of Science and Technology,respectively.His research interests include memristor,stability analysis of nonlinear systems,and association memory.Corresponding author of this paper.E-mail:hustgangbao@ctgu.edu.cn

Yuanyuan Chen received the B.S.degree from the College of Science and Technology,China Three Gorges University in 2016.Now she is a postgraduate student and pursuing for M.S.degree at the School of Electrical Engineering and New Energies,China Three Gorges University.Her current research interests include microgrid optimization scheduling and stability analysis.E-mail:pretty.yuanzi@qq.com

Siyu Wen received the B.S.degree in water resources and hydropower engineering from the College of Science and Technology,China Three Gorges University in 2016.Now,she is currently working toward the M.S.degree at the School of Electrical Engineering and New Energies,China Three Gorges University.Her current research interests include hydropower dispatching and unit commitment optimization.E-mail:215341796@qq.com

Zhicen Lai received the B.S.degree in electrical engineering and its automation(focus on transmission line),China Three Gorges University in 2016. She is currently working toward the M.S.degree at the School of Electrical Engineering and New Energies,China Three Gorges University,Yichang,China.Her current research interests include microgrid control and stability analysis.E-mail:2512991452@qq.com