一种健壮的超像素跟踪算法①
郭 利,周盛宗,3,付璐斯,于志刚
1(中国科学院 福建物构所,福州 350002)
2(福建师范大学 数学与计算机科学学院,福州 350117)
3(中北大学 计算机与控制工程学院,太原 030051)
一种健壮的超像素跟踪算法①
郭 利1,2,周盛宗1,2,3,付璐斯1,3,于志刚1,3
1(中国科学院 福建物构所,福州 350002)
2(福建师范大学 数学与计算机科学学院,福州 350117)
3(中北大学 计算机与控制工程学院,太原 030051)
在目标跟踪中,传统的超像素跟踪算法在发生遮挡等情况后,会将非目标超像素标记为目标加入到特征空间. 在对候选样本置信度计算中,利用特征空间中最近邻超像素来划定样本中超像素的簇归属会产生错误; 而依据的近邻超像素数量过多时,又会造成分类误差的积累. 为解决上述问题,本文提出一种健壮的超像素跟踪算法. 本算法以贝叶斯算法为框架,首先,将前几帧进行超像素切割,提取特征并使用均值漂移聚类算法和基于超像素的外观表示模型进行分类和计算类置信度,放入特征空间中. 其次,根据接下来几帧的平均中心误差确定最佳近邻数目. 最后,在跟踪过程中,对获取帧的指定区域进行超像素切割,提取特征、进行软分类和计算置信度; 根据上一帧目标位置进行高斯采样,累加样本内超像素置信度,获得样本置信度; 在发生严重遮挡时,不进行滑动窗口更新和外观模型修改,使用当前模型继续跟踪. 与传统的最近邻超像素算法相比,本算法能够有效提升跟踪成功率和降低平均中心误差.
最佳近邻数目; 软分类; 目标跟踪; 均值漂移算法; 置信度; 遮挡
运动目标跟踪是机器视觉研究的一个基本课题,在视频监控、运动分析、人机交互和自动驾驶等领域中发挥着重要作用. 目标跟踪是从一系列图像中,确定目标在每帧图像中的位置、方向、面积、形状等. 由于受光照强弱、相机颠簸、物体遮挡、形态变化、速度调整等因素的影响,目标外观发生了很大的变化,从而使得目标跟踪非常有难度. A.Yilmaz等[1]认为目标跟踪主要分为点跟踪、核跟踪、剪影跟踪三类. 点跟踪主要包括确定法和统计法,代表性的方法有MGE[2]、GOA[3]、卡尔曼滤波[4]、JPDAF[5]、PMHT[6]等; 核跟踪主要包括基于模板和密度的外观模型、多角度外观模型等,前者的代表性方法有Mean-Shift[7]、KLT[8]、分层[9],后者的代表性方法有特征值跟踪[10]、支持向量机跟踪[11]; 剪影跟踪主要包括轮廓演变、形状匹配,前者的代表性方法有状态空间模型[12]、变量方法[13]、启发方法[14]. 这些数算法大都是围绕着目标表示、特征选择、运动建模、外观表示、形态变化等五个方面进行改进,在特定场景下取得了不错的效果. 在目标运动中,自适应外观算法[15-20]能够很好的表示外观的变化,但基于低层特征的自适应外观算法在前后帧的关联上表现很差; Kwon等[21]提出的基于多运动模型和改进观测模型的粒子滤波框架能较好的处理遮挡、尺度、光照和尺度等因素引起的外观变化,由于未区分目标、背景,会出现跟踪目标丢失. Ren等[22]提出的超像素跟踪算法,使用Delaunay三角化和条件随机场单独对每帧完整图做区域匹配,能够对前景、背景有限分割,但仍然无法处理跟踪过程中的遮挡、复杂背景等问题.Yant等[23]提出的健壮超像素跟踪算法,在有限遮挡、光照变化、姿态变化、复杂背景等情况下,都取得不错效果,但由于遮挡等情况下,划定到特征空间中的超像素在目标、背景划分及簇归属上会存在一些错误,仅根据特征空间中离其最近的超像素的簇归属来划定簇是错误的; 同样,依据的超像素数量过多时,又会造成分类误差的积累,有限数目超像素来确定当前超像素簇归属会更有效. 因此,提出一种健壮的超像素跟踪算法,该算法根据历史样本匹配度寻找最佳近邻数目,使用贝叶斯框架构造联合外观模型,使用基于超像素的判别型外观模型将前景对象从背景中区分开来.
1 算法的主要部分
1.1 确定最佳近邻个数
如图1,K=5时,黄色椭圆的最近5个邻居是2个绿色正方形和3个红色三角形,K-近邻判别法判定黄色椭圆与红色三角形同类; K=9时,黄色椭圆的最近9个邻居是5个绿色正方形、3个红色三角形和1个深红梯形,K-近邻判别法判定黄色椭圆与绿色正方形同类.
图1 不同近邻对分类的影响

其中,

1.2 贝叶斯跟踪框架
给定t时刻的状态Xt、所有的观测值Y1:t,设定归一化项为α,计算最大后验分布[23],具体如式(2).

1.3 基于超像素的外观区分模型
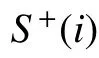

正值越大,簇属于目标的置信度越高,反之亦然.
1.4 基于k近邻的置信度计算
当新帧到来时,使用高斯采样提取目标的周边区域,根据当前超像素与簇空间中超像素的距离来计算置信度,并确定置信度最高的样本为跟踪目标. 在遮挡等情况下,超像素在目标、背景的划分上较难,仅依据空间中最近邻的超像素来划定簇归类不准确. 因为置信度与两个因素有关: 距离较近的超像素所属的簇、在特征空间中超像素与簇中心的距离. 取定近邻超像素的个数为 k=k*,距离分别为D1,D2,...,Dk,则:
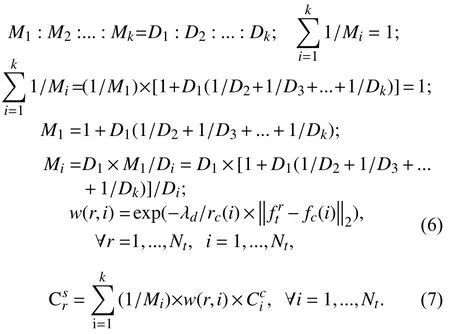
1.5 观察和运动模型
设定运动模型为高斯分布[23],
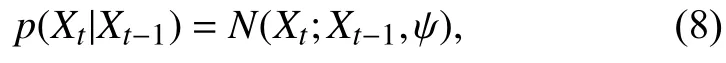

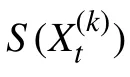
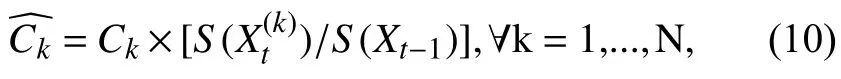
观测模型[23]:
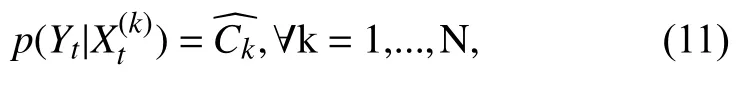
1.6 针对遮挡和漂移的在线更新
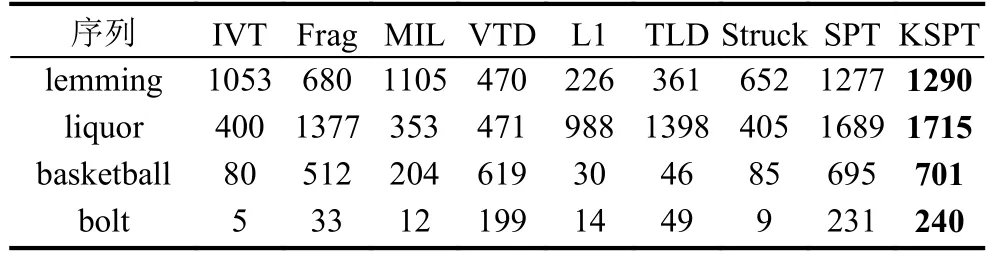
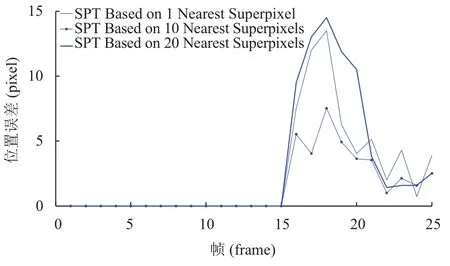
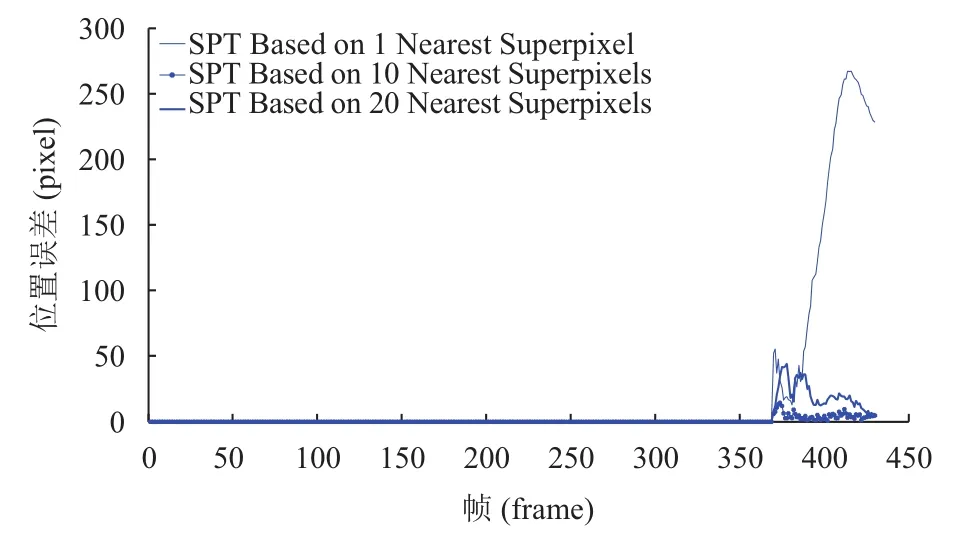
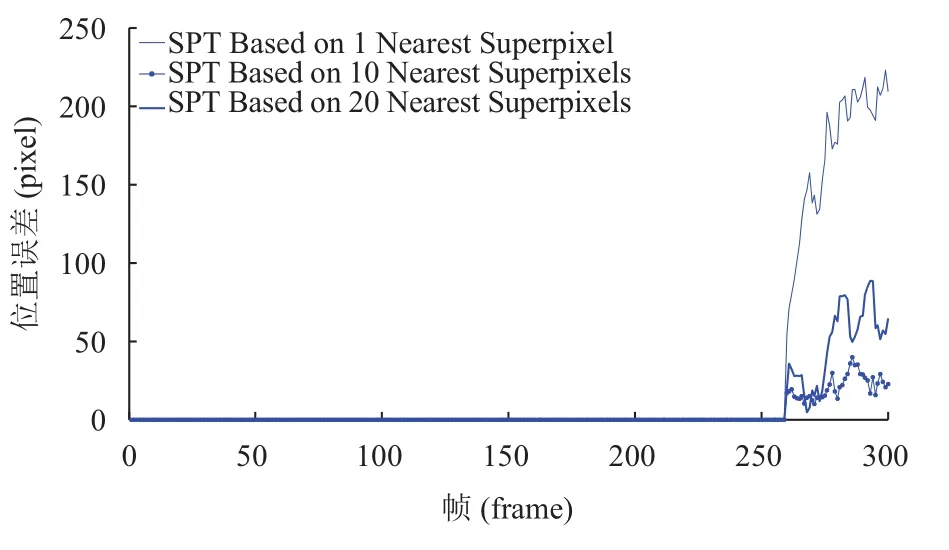
使用滑动窗口机制进行跟踪,每U帧,添加一个新帧到H帧序列中,并删除序列中的第k帧(k 大于零时,表示当前帧的平均准确率评估的置信度比保存序列中的规范化置信度的平均值小,超过一定阈值时,候选区域可能属于背景区域,或发生严重遮挡. fort= 1 tom(设定m=4) 1) 初始化t帧的各个参数. End fort=m+1 ton(设定n=15) 1) 切割Xt周边区域为Nt个超像素,提取特征. 使用公式(6)、(7)计算目标背景置信度. 4) 依据公式(1),获取最佳后验时的近邻数目k. 5) 使用公式(12)来探测严重或完全遮挡. 6) 每隔U帧,添加一帧到更新序列. 7) 每隔W帧,更新一次外观模型. fort=n+1 to 帧数 1) 切割Xt周边区域为Nt个超像素,提取特征. 使用公式(6)、(7)计算值目标背景置信度. 5) 使用公式(12)来探测严重或完全遮挡. 6) 每隔U帧,添加一帧到更新序列. 7) 每隔W帧,更新一次外观模型. End 实验在CPU为3.6 GHZ、内存为8 G的PC机上进行,采用 Matlab2012b、Microsoft Visual Studio 2010混合编程实现. HIS颜色空间降低了像素受光照变化的影响,在区分不同超像素方面,比其他颜色空间的区分能力更强,使用HIS颜色空间中的规范化图表作为每个超像素的特征. 使用SLIC算法切割图片时,空间近似权值设置为10,超像素数目设置为300,均值漂移聚类算法的尺度设置为0.18. 在初始阶段,为了获取训练集,前4帧的目标区域可以通过目标定位器或手动获取. 按照经验,设置H=15,U=1,W=10,速度变化 σc=7.6,尺度变化 σs=7. 为简化遮挡探测,设置 µc=0.5. 表1对比了IVT[25](不断学习的健壮跟踪)、Frag[18](使用积分直方图的基于碎片的健壮跟踪算法)、MIL(在线的多实例学习的视觉跟踪)、VTD[26](视觉跟踪分解)、L1[27](使用加速接近梯度算法的实时健壮L1跟踪)、TLD[28](基于机构约束的增强二进制分类器)、Struck[29](基于核的机构性输出跟踪)、SPT[23](基于超像素的目标跟踪)、KSPT(基于有限学习的软分类超像素跟踪算法)在Lemming、liquor、basketball、bolt等数据集上中心定位错误的帧数上,KSPT都是最少的. 表1 中心定位错误的帧数 表2对比了 IVT[25]、Frag[18]、MIL、VTD[26]、L1[27]、TLD[28]、Struck[29]、SPT[23]、KSPT 在 Lemming、liquor、basketball、bolt等数据集上成功跟踪到的帧数,KSPT 都是最多的. 表2 成功跟踪到的帧数 表3对比了SPT[23]、KSPT在surfing1、singer1、woman、girl_move等数据集上的成功率,KSPT比SPT都有了很大提升. 这是因为超像素空间中,各类在簇的划分上,并不绝对准确,最近邻超像素跟踪算法只依据与超像素空间最近邻的超像素进行分类,易发生分类错误. 而通过训练过程,学习出最佳的近邻数目,引导超像素分类,一定程度增加了待分类的超像素的容错程度,提升了超像素置信度计算的准确度,从而提高算法对目标的跟踪能力. 表3 成功率 (%) 图2中,不同近邻个超像素的SPT在Lemming数据集第16~25帧上的位置误差情况,1、10、200近邻个超像素的SPT对应位置总误差59.3936、36.3729、70.3006像素; 10近邻个超像素(*型实线)的SPT表现最好,其他近邻的SPT总误差相对较大. 在此10帧的跟踪中,10近邻超像素的SPT表现更为稳定,误差相对最小. 根据该 10 帧,推测出 KSPT 中最佳 K=10; 而事实上,在26~800帧上,10近邻的SPT表现也最好,其中370~430、460~600帧表现最明显,见图3、图4. 图2 不同近邻个超像素的SPT的位置误差 图3 不同近邻个超像素的SPT的位置误差 图3中,不同近邻个超像素的SPT在Lemming数据集第370~430帧上位置误差,1、10、200近邻个超像素的SPT对应位置总误差9088.5、275.3、12043像素; 10近邻个超像素(*型实线)的SPT表现最好,其他近邻的SPT总误差相对较大. 图4中,不同近邻个超像素的SPT在Lemming数据集第460~600帧上的位置误差情况,1、10、200近邻个超像素的SPT对应位置误差31904、779、2594像素. 图4 不同近邻个超像素的SPT的位置误差 图5中,不同近邻个超像素的SPT在skating1数据集第16~25帧上位置误差,1、10、20近邻个超像素的SPT对应位置总误差为60.8563、40.4681、56.9368像素; 10近邻个超像素(*型实线)的SPT表现最好,其他近邻的SPT总误差相对较大. 在此10帧的跟踪中,10近邻超像素的SPT表现更为稳定,误差相对最小. 根据该 10 帧,推测出 KSPT 中最佳 K=10; 而事实上,10近邻超像素的SPT在26~300帧上,10近邻的SPT表现也很好,见图6、图7. 在75~230帧上,20近邻的SPT发生跟踪漂移,跟踪效果很差,见图6;260~300帧,1近邻的SPT发生跟踪漂移,跟踪效果也很差,见图7. 图5 不同近邻个超像素的SPT的位置误差 图6 不同近邻个超像素的SPT的位置误差 图7 不同近邻个超像素的SPT的位置误差 图6中,不同近邻个超像素的SPT在skating1数据集第75~230帧上位置误差情况,1、10、20近邻个超像素的SPT对应位置总误差3848、3439、22189像素. 图7中,不同近邻个超像素的SPT在第260~300帧上位置误差情况,1、10、20近邻个超像素的SPT对应位置总误差6952.6、862.7、1968.5像素;10近邻个超像素(*型实线)的SPT表现最好,其他近邻的SPT总误差相对较大. 图8的Lemming数据集中,存在光照变化、尺度变化、不同程度遮挡、快速运动、离面旋转等情况.在这种背景下,基于历史外观模型的IVT由于外观模型不能很好的应对外观变化,所以在目标姿态和尺度都变化不大时表现良好,而在姿态和尺度发生较大变化时表现不佳. 基于边信息的TLD由于未使用基于中层特征的外观模型,所以在跟踪姿态、尺度发生较大变化的目标时效果不如KSPT算法. 在跟踪目标发生遮挡的第332帧、快速运动的第399帧、离面旋转的第997、1299帧,KSPT均表现出相当的优异性. 图8 KSPT(细线)、TLD(粗线)、IVT(虚线)在 Lemming 数据集第332、399、997、1299帧上的跟踪结果. 图9 KSPT(细线)、TLD(粗线线)、IVT(虚线)在 bolt数据集第20、92、222、350帧上的跟踪结果. 图9的Bolt数据集中,存在不同程度遮挡、变形、平面内运动、离面运动等情况. 在这种背景下,基于边信息的TLD、基于历史外观模型的IVT的跟踪效果却差了很多,再次印证KSPT依托的中层特征外观模型的优越性. 在跟踪目标因为运动引起形变的第20、92、222、350帧,KSPT均表现出相当的优异性. 针对现有超像素跟踪算法仅依据特征池中最近邻超像素划定当前超像素簇归属造成分类错误的问题,本文提出一种健壮的超像素跟踪算法. 该算法通过历史样本的平均中心误差,确定最佳近邻个数. 根据最佳近邻个超像素划定当前超像素的簇归属,减弱了部分遮挡情况下特征置信度对候选样本的干扰,从而有效提升中心定位成功率和成功跟踪到的帧数. 考虑到均值漂移聚类算法的耗时性,正在探索其他有效、快速的算法; 运动模型中的速度、尺度参数都是经验值,不能实现自适应变化,尤其是出现撑杆跳等快速运动情况就很难发挥作用. 另外,鉴于简单HIS颜色特征尚且取得不错的效果,相信更好特征的出现,一定能够很好的提升跟踪效果. 1Yilmaz A,Javed O,Shah M. Object tracking: A survey.ACM Computing Surveys,2006,38(4): 13. [doi: 10.1145/1177352] 2Salari V,Sethi IK. Feature point correspondence in the presence of occlusion. IEEE Trans. on Pattern Analysis and Machine Intelligence,1990,12(1): 87–91. [doi: 10.1109/34.41387] 3Veenman CJ,Reinders MJT,Backer E. Resolving motion correspondence for densely moving points. IEEE Trans. on Pattern Analysis and Machine Intelligence,2001,23(1):54–72. [doi: 10.1109/34.899946] 4Broida TJ,Chellappa R. Estimation of object motion parameters from noisy images. IEEE Trans. on Pattern Analysis and Machine Intelligence,1986,8(1): 90–99. 5Bar-Shalom Y,Fortmann TE. Tracking and data association.San Diego,CA,USA: Academic Press Professional,Inc.,1988. 6Streit RL,Luginbuhl TE. Maximum likelihood training of probabilistic neural networks. IEEE Trans. on Neural Networks,1994,5(5): 764–783. [doi: 10.1109/72.317728] 7Comaniciu D,Ramesh V,Meer P. Kernel-based object trac-king. IEEE Trans. on Pattern Analysis and Machine Intelligence,2003,25(5): 564–577. [doi: 10.1109/TPAMI.2003.1195991] 8Shi JB,Tomasi. Good features to track. 1994 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,1994. Seattle,WA,USA. 1994. 593–600. 9Tao H,Sawhney HS,Kumar R. Object tracking with Bayesian estimation of dynamic layer representations. IEEE Trans. on Pattern Analysis and Machine Intelligence,2002,24(1): 75–89. [doi: 10.1109/34.982885] 10Black MJ,Jepson AD. EigenTracking: Robust matching and tracking of articulated objects using a view-based representation. International Journal of Computer Vision,1998,26(1):63–84. [doi: 10.1023/A:1007939232436] 11Avidan S. Support vector tracking. Proc. of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2001. Kauai,HI,USA. 2001. 184–191. 12Isard M,Blake A. CONDENSATION-Conditional density propagation for visual tracking. International Journal of Computer Vision,1998,29(1): 5–28. [doi: 10.1023/A:1008 078328650] 13Bertalmio M,Sapiro G,Randall G. Morphing active contours: A geometric approach to topology-independent image segmentation and tracking. Proc. of 1998 International Conference on Image Processing. Chicago,IL,USA. 1998.318–322. 14Kang JM,Cohen I,Medioni G. Object reacquisition using invariant appearance model. Proc. of the 17th International Conference on Pattern Recognition. Cambridge,UK. 2004.759–762. 15Jepson AD,Fleet DJ,El-Maraghi TF. Robust online appearance models for visual tracking. IEEE Trans. on Pattern Analysis and Machine Intelligence,2003,25(10): 1296–1311. [doi: 10.1109/TPAMI.2003.1233903] 16Lim J,Ross DA,Lin RS,et al. Incremental learning for visual tracking. Advances in Neural Information Processing Systems.Vancouver,Canada. 2004. 793–800. 17Collins RT,Liu YX,Leordeanu M. Online selection of discriminative tracking features. IEEE Trans. on Pattern Analysis and Machine Intelligence,2005,27(10): 1631–1643. [doi:10.1109/TPAMI.2005.205] 18Adam A,Rivlin E,Shimshoni I. Robust fragments-based tracking using the integral histogram. 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York,NY,USA. 2006. 798–805. 19Grabner H,Leistner C,Bischof H. Semi-supervised on-line boosting for robust tracking. Proc. of the 10th European Conference on Computer Vision: Part I. Marseille,France.2008. 234–247. 20Kwon J,Lee KM. Tracking of a non-rigid object via patchbased dynamic appearance modeling and adaptive basin hopping monte carlo sampling. IEEE Conference on Computer Vision and Pattern Recognition(CVPR 2009).Miami,FL,USA. 2009. 1208–1215. 21Kwon J,Lee KM. Visual tracking decomposition. 2010 IEEE Conference on Computer Vision and Pattern Recognition(CVPR 2010). San Francisco,CA,USA. 2010. 1269–1276. 22Ren XF,Malik J. Tracking as repeated figure/ground segmentation. IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis,MN,USA. 2007. 1–8. 23Yang F,Lu HC,Yang MH. Robust superpixel tracking. IEEE Trans. on Image Processing,2014,23(4): 1639–1651. [doi:10.1109/TIP.2014.2300823] 24陈桂景,王尧弘. 自适应近邻判别分析. 数学物理学报,1996,16(S1): 9–19. 25Ross DA,Lim J,Lin RS,et al. Incremental learning for robust visual tracking. International Journal of Computer Vision,2008,77(1-3): 125–141. [doi: 10.1007/s11263-007-0075-7] 26Kwon J,Lee KM. Visual tracking decomposition. 2010 IEEE Conference on Computer Vision and Pattern Recognition(CVPR 2010). San Francisco,CA,USA. 2010. 1269–1276. 27Bao CL,Wu Y,Ling HB,et al. Real time robust L1 tracker using accelerated proximal gradient approach. IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2012). Providence,RI,USA. 2012. 1830–1837. 28Kalal Z,Matas J,Mikolajczyk K. P-N learning: Bootstrapping binary classifiers by structural constraints. 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2010). San Francisco,CA,USA. 2010. 49–56. 29Hare S,Golodetz S,Saffari A,et al. Struck: Structured output tracking with kernels. IEEE Trans. on Pattern Analysis and Machine Intelligence,2016,38(10): 2096–2109. [doi:10.1109/TPAMI.2015.2509974] Robust Superpixes Tracking Method GUO Li1,2,ZHOU Sheng-Zong1,2,3,FU Lu-Si1,3,YU Zhi-Gang1,3 1(Fujian Institute of Research on the Structure of Matter,Chinese Academy of Sciences,Fuzhou 350002,China) During the object tracking,when occlusion occurs,the traditional superpixel tracking algorithm will add the superpixels of the non-target area into the feature space. In the calculation of the candidate sample confidence,the nearest neighbor superpixel in the feature space is used to delimit the cluster attribution of the superpixels in the sample,and the accumulation of the classification error is caused by the excessive number of neighboring superpixels. To solve the problems above,we propose a robust superpixels tracking method. This algorithm uses Bayesian algorithm as the framework. Firstly,we slice the first few frames into superpixels,extract the feature,use the mean shift clustering algorithm and representation model based on superpixel to classify and calculate the class confidence value,and put the feature into feature space. Secondly,the suitable numbers of neighbors can be found with the mean center error of next few frames. Last but not least,during the tracking process,the superpixel is segmented in the specified area of the acquired frame,to extract the feature. The cluster is confirmed with soft classification and the confidence value is calculated. According to the previous frame target position,the Gaussian sampling is collected. We can obtain the sample confidence value with the accumulation of the confidence value. In case of severe occlusion,the sliding window update and the appearance model modification are not carried out,and we continue to use the current model to track. Compared with the traditional tracking algorithm based on nearest superpixel,the algorithm can effectively improve the tracking success rate and reduce the average center errors. best number of nearest neighbors; soft classification; object tracking; meanshif; confidence; occlusion 郭利,周盛宗,付璐斯,于志刚.一种健壮的超像素跟踪算法.计算机系统应用,2017,26(12):130–136. http://www.c-s-a.org.cn/1003-3254/6120.html 2017-03-16; 修改时间: 2017-04-05; 采用时间: 2017-04-17
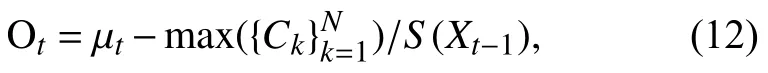
2 算法的实现过程
2.1 初始化
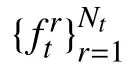
2.2 学习近邻数目
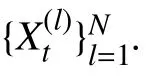
2.3 跟踪
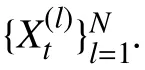
3 实验结果及分析
3.1 实验设置
3.2 实验结果及分析






4 结语
2(College of Mathematics and Computer Science,Fujian Normal University,Fuzhou 350117,China)
3(School of Computer and Control Engineering,North University of China,Taiyuan 030051,China)

