基于水流扰动参数的复杂河湖系统藻类数值模拟
闵志华+王晓琴+李傲
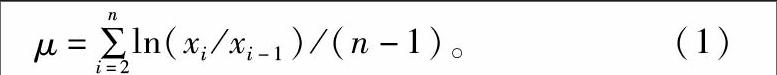
摘要: 为研究水流扰动对藻类生长的影响,基于室内藻类生长动力学试验,提出藻类生长过程中的水流扰动参数α,并对藻类生长公式进行修正;运用一维河网与二维湖泊耦合的藻类生长动力学模型对太湖西北部重污染区藻类生长的时空分布特征进行动态模拟。结果表明:(1) 水动力条件对藻类生长影响明显,研究区内东西向河流流速较大,水流扰动强,藻类浓度低于南北向河流;(2)各研究断面藻类浓度均呈现时间分布不均性,枯季(11月至次年4月)水流扰动较弱,为藻类生长创造较好的环境,藻类平均浓度较洪季(5月至10月)增加了9.22%;(3)河湖系统内湖口区水流条件更适宜藻类生长,位于湖口区的S2与S4点位浓度平均较河网区增加了18.5%。
关键词: 太湖;河湖系统;富营养化;藻类;扰动;模型
中图分类号: X171 文献标志码: A
文章编号:1002-1302(2017)22-0264-05
水体富营养化导致的水华暴发是全球范围内面临的一项重要环境问题[1],藻类等浮游植物的大量生长是其发生的重要原因[2]。藻类生长数值模拟是蓝藻水华预警的重要基础性工作,对于维持健康稳定的水生态系统具有重要意义。诸多学者开展了藻类数值模拟研究。逄勇等进行了太湖藻类的数值模拟,探讨了太湖藻类的动态变化机制[3-4];Cole等构建了包括温度、营养盐及溶解氧等状态变量在内的富营养化模型,开展了湖湾及浅水湖泊的藻类生长数值模拟[5-7]。这些成果提高了藻类数值模拟的水平,但基本没有考虑水流扰动对藻类生长数值模拟的影响。同时,关于藻类数值模拟的研究大多围绕单一湖泊或河道开展,对于河网纵横交错、湖泊较多的复杂河湖系统所进行的藻类数值模拟研究未见报道,这类地区湖泊与河网之间存在着频繁的物质与能量交换,藻类数值模拟更为复杂[8-9]。本研究提出了影响藻类生长的水流扰动参数α,运用一维河网与二维湖泊耦合的藻类生长动力学模型对太湖西北部复杂河湖系统藻类生长的时空分布特征进行了动态模拟,旨在为藻类生长数值模拟和水华预警提供依据。
1 研究区域
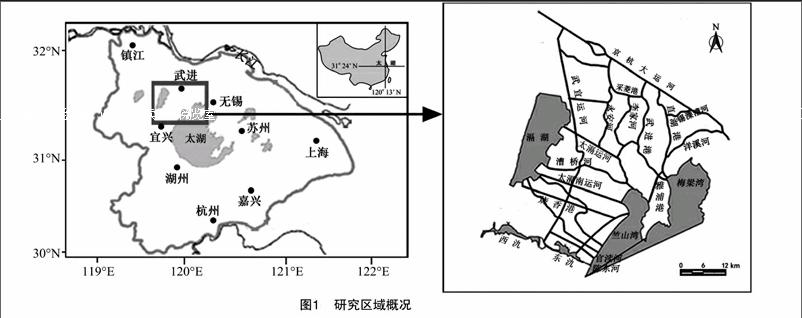
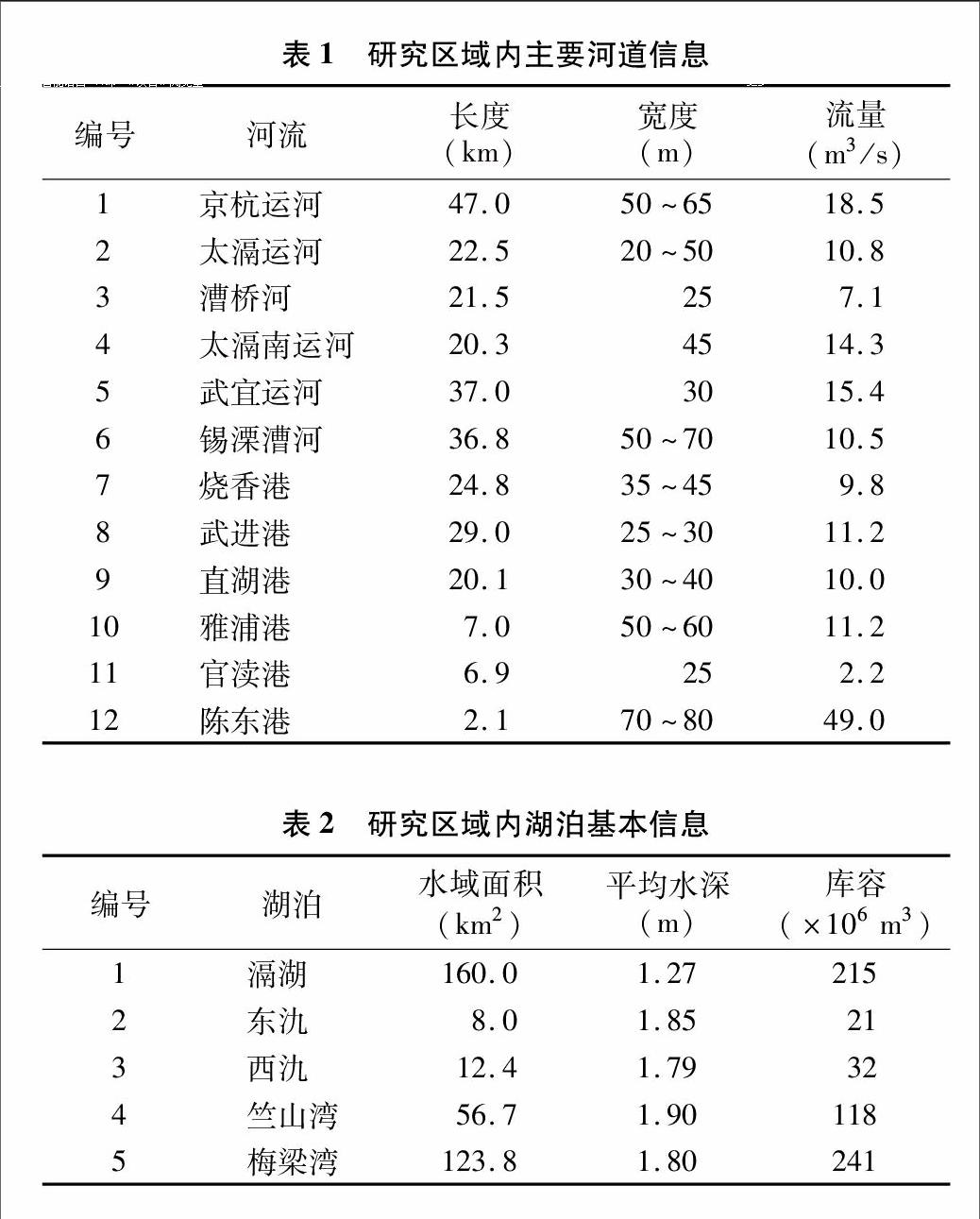
研究区为太湖西北部重污染区,该区域河流众多并有多个湖泊,属于典型的河湖系统。研究范围北起京杭大运河,南至江苏省宜兴市东、西氿,西至滆湖,东至太湖梅梁湾和竺山湾,涉及江苏省无锡市惠山、北塘、南长、新区、崇安、滨湖等6个区和宜兴市,以及江苏省常州市钟楼、天宁、戚墅堰、新北、武进等5个区,共41个镇,56个街道。研究区域总面积为 5 272 km2,占太湖流域的5.4%。该河网区水质达标率为17%,占太湖入湖污染物通量的 80% 左右[10],是影响太湖湖体,特别是梅梁湾、竺山湾水质的主要区域(图1)。该河湖系统内主要有12条河流,其中入太湖河流7条,入太湖竺山湾的河流分别为太滆运河、太滆南运河、漕桥河、官渎港、陈东港,入太湖梅梁湾的河流分别为直湖港、武进港;出滆湖河流4条,分别为太滆运河、漕桥河、太滆南运河(殷村港)、烧香港。研究区内河道见表1。河湖系统内主要湖泊有滆湖、东氿、西氿、太湖竺山湾、梅梁湾。滆湖是该区域重要的行蓄洪湖泊,位于太湖西北部,进出水量基本平衡,换水周期较短,为每年7.03次。东氿、西氿位于太湖以西,滆湖以南,是流域众多河流入湖前所必经的重要湖泊。竺山湾和梅梁湾为太湖北部的2个湖湾,竺山湾为太湖西北部的半封闭性富营养湖湾,北起百渎口,南至马山咀一线;梅梁湾是太湖北部的湖湾,占太湖总面积的5.2%。2个湖湾是承接经入湖河流携带的大量陆域污染物的主要水域。研究区各湖泊基本信息见表2。
2 藻类生长动力学试验
2.1 试验条件与方法
为了研究水流扰动对藻类生长的影响,试验过程中维持温度、光照、水质等藻类生长影响因子的一致性,通过改变恒温振荡箱转速来代替水流扰动。试验过程中选择引起蓝藻暴发的优势藻种铜绿微囊藻作为试验藻种[11-12]。藻种来自中国科学院水生生物研究所藻种库,保存在20 ℃的光照培養箱中。运用pH值为8.6的MA培养基对铜绿微囊藻进行单独培养[13]。在具硅胶塞的250 mL锥形瓶中加入100 mL培养基,高压灭菌,将预先培养至对数生长期的藻种离心、洗涤后接种,使得试验培养液中藻类的初始密度为 5.0×104 cell/mL,接种后将锥形瓶放入恒温振荡箱培养;布置6个培养样品,每个样品分别设置转速0、60、90、120、150、200 r/min,各转速重复试验2次;试验过程所有操作均在无菌条件下进行,不同扰动强度下,均维持温度为25 ℃,光照度为2 000 lx,光—暗周期为12 h—12 h。自接种当日起,每天在同一时间取样, 每种样品取0.1 mL藻液置于0.1 mL微囊计数
板中用双目显微镜进行多次计数,取平均值,直到藻衰败为止。以藻类生长期内平均比增长率作为藻类在某条件下增长率的估计值[14],公式为
式中:μ为藻细胞比增长率;n为藻类生长期时间;xi为当日藻细胞数;xi-1为前1 d的藻细胞数。
2.2 试验结果分析
根据试验结果,绘制不同扰动强度下藻类生长过程线及平均增长率(图2)。结果表明:(1)在不同转速下,铜绿微囊藻生长情况随时间分布规律基本一致,可分为生长期(第1~5天)、稳定期(第5~8天)、衰亡期(第8天后)。(2)在静止条件下,藻类生长过程中没有明显的稳定期,仅有生长期与衰亡期,且生长期较扰动条件下延长了1倍。(3)在静止条件下,藻细胞数为0.7×106个/mL;当转速为60、90 r/min时,藻细胞数明显增加,分别达1.50×106、0.84×106个/mL;当转速增加至120 r/min以上时,藻细胞数明显减少。(4)在静止条件下,铜绿微囊藻增长率较低,为0.29;当转速为60、90 r/min 时,增长率分别达0.57、0.71;当转速增加至 120 r/min 以上时,藻类增长率呈现降低趋势。综上所述,扰动转速对铜绿微囊藻的生长有影响,适当的扰动转速可以促进铜绿微囊藻的生长,而静止状态和过高的扰动转速对藻类生长有抑制作用。endprint
2.3 水流扰动参数确定
由于室内试验条件与野外环境存在差异,如何将室内扰动转速转换成野外环境中的水体流速尤为关键。本研究选择起悬泥沙浓度作为中间因子,通过野外同步水流泥沙监测及同步泥沙起悬试验,建立了扰动转速与水体流速的等量转化关系。以上转化建立在“引起相同起悬泥沙浓度的室内扰动转速与水体流速其动力效应是相当的”。野外同步监测分别在2012年1月(枯季)与7月(洪季)2个典型季节开展,共设置了24个同步监测点位,其中湖体6个,河网区18个(图3)。基于各监测垂线0.8H处的水流泥沙监测结果,建立水体流速与起悬泥沙浓度关系。室内泥沙起悬试验同样设置0、60、90、120、150、200 r/min共6个转速处理,试验用水和泥样完全取自野外监测点位;每组扰动设置2个重复开展起悬试验,根据试验结果,建立室内扰动强度与起悬泥沙浓度关系曲线。基于野外实际流速、室内扰动强度与起悬泥沙浓度的相关性建立起两者间的转换方程;结合藻类生长动力学试验结果,绘制藻类生长水流扰动参数曲线(图4),具体数学方程如下:
式中:α为水流扰动参数;f(u)与g(u)分别为不同流速区间的相关函数;u为水体流速,m/s;uopt为最适宜水体流速,根据试验结果,取0.15 m/s。
3 河湖藻类数学模型
3.1 基本方程
太湖西北部重污染区河湖系统水流复杂,藻类数值模拟采用一维河网与二维湖泊耦合模型。一维模型实现河网区水流过程与藻类生长过程的模拟计算,同时为二维湖泊模型提供相关的计算边界;二维模型计算范围主要为系统内河网受纳湖泊,包括东氿、西氿、太湖竺山湾和梅梁湾,二维模型用于河湖交换条件下湖泊藻类生长的数值模拟。
3.1.1 一维河网藻类生长模型
一维模型选用TN、TP、Chl-a作为主要计算指标,基于生态动力学方程建立综合考虑光照、温度、营养盐及水动力条件等多因子耦合的一维河网区藻类生长模型,其中光照、温度等参数在藻类生长参数模块中统一考虑,模型基本控制方程如下:
式中:t为时间坐标,s;x为顺河向长度坐标,m;Q为流量,m3/s;Z为水位,m;U为断面平均流速,m/s;n为糙率;A为过流断面面积,m2;B为主流断面宽度,m;BW为水面宽度,m;R为水力半径,m;g为重力加速度,m2/s;q为旁侧入流流量,m3/s。N、P、Chl-a为断面总氮、总磷、叶绿素a的垂线平均浓度,mg/L;Ex为纵向分散系数;Kn、KP为N、P污染物降解系数;SChl-a、SN、SP为叶绿素a和氮、磷的源汇项。
3.1.2 二维湖泊藻类生长模型
二维湖泊藻类生长模型在有限体积法框架下构建,模型同样耦合了光照、温度、营养盐及水动力条件等多项藻类生长影响因子,具体控制方程如下:
式中:h为水深;u、v为x、y方向垂线平均水平流速分量;g为重力加速度;s0x为x向的河底底坡;s0y为y向的河底底坡;sfx为x向摩阻底坡;sfy为y向摩阻底坡;ΔT为温差;tx、ty分别为水温在x、y向扩散系数;ρ和Cp分别为水的密度和比热;Ks为水面综合散热系数,模型采用Gunnerberg经验公式计算水面综合散热系数。N、P、Chl-a分别为总氮、总磷、叶绿素a的垂线平均浓度;SN、SP、SChl-a分别为氮、磷和叶绿素a的源汇项。
方程(3)、(4)中,SN、SP、SChl-a可具体表达为以下形式:
式中:RN、RP分别为底泥中氮、磷的释放项;SEDN、SEDP分别为氮、磷的沉降项;CN、CP分别为藻类死亡分解对氮、磷的贡献项;UN、UP分别为藻类对氮、磷的吸收项;μ为藻类的生长率;sed为藻类的沉降率;d为藻类的损失率。水流扰动参数α对藻类生长率μ进行修正如下:
式中:μmax为藻类最大生长率;f(T)为温度函数;f(I)为光照函数;f(N)与f(P)为氮、磷营养盐函数;α为水流扰动参数,按照公式(2)计算取值。
3.2 数值解法
河湖系统耦合模型采用分段求解。一维河网水动力微分方程组采用四点隐式差分格式数值求解,对水动力方程组以Preissmann四点线性隐式差分格式将其离散,辅以连接条件,形成河道方程,以微段、河段、汊点三级联解的方法[15]求解。TN、TP、Chl-a求解采用隐式迎风格式,时间项采用前差分对每个单一河道进行离散[16],将整个河网TN、TP、Chl-a浓度离散成节点和断面水质浓度进行数值求解。二维湖泊模型将水流水质方程与藻类生长方程联合求解,公式(4)可统一写为以下形式[17-19]:
式中:q为守恒物理量;f(q)、g(q)分别为x、y方向通量;b(q)为源汇项。
在任意形状的单元Ω上采用有限体积法对式(4)进行积分离散,运用FVS格式求解法向数值通量。具体解算过程及模型率定验证过程详见参考文献[20-21]。
3.3 率定验证
基于2012年1月(枯季)、7月(洪季)的水文水质同步监测结果,对所建耦合数学模型进行率定验证。计算区域为研究区域内的河湖系统,运用Gambit软件对湖区进行无结构网格剖分。以西部滆湖、北部京杭运河实测水量水质作为计算边界。考虑计算稳定性及精度,取时间步长为1 s。结果表明,计算结果与实测值拟合效果较好,COD、氨氮的平均相对误差分别为22.0%、17.9%。所建模型能夠较准确地反映河湖系统水量水质动态变化特征。
4 河湖系统藻类时空分布规律
基于所建的考虑水流扰动参数的一维、二维耦合藻类模型,对太湖西北部重污染区河湖系统藻类时空分布规律进行数值模拟。根据太湖流域茅东、丹阳、溧阳、赵村、宜兴、常州、陈墅等40多个雨量站近10年时间序列内降水量资料频率分析结果,确定2011平水年为计算典型年,以西部滆湖、北部京杭运河实测TN、TP、Chl-a浓度作为计算初始边界,对系统内藻类生长及迁移过程进行数值模拟。选择6个典型断面对藻类时空分布特征进行分析,分别为太滆南运河上游S1 (31°30′37.18″N,119°48′45.92″E)、竺山湾湖口S2 (31°27′12.31″N,120°0′25.39″E)、直湖港河流上游S3 (31°40′20.14″N,120°8′12.13″E)、梅粱湾湖口S4 (31°30′31.44″N,120°7′2167″E)、永安河下游S5 (31°42′8.90″N,119°59′14.91″E)、太滆运河S6 (31°34′20.31″N,119°57′14.94″E),其中S2与S4为湖泊点位,其余为河网点位(图5)。endprint
计算结果表明:(1) 平水年水文条件下,S1~S6断面全年平均Chl-a浓度分别为8.50、10.32、10.02、10.92、11.49、9.15 mg/m3;S1与S6断面藻类水平相对较低,而S4与S5断面Chl-a浓度明显增加,S2与S3断面浓度处于中间水平(图6)。根据多年实测水文数据,研究区域内东西向河流流速大于南北向河流,太滆运河、太滆南运河等东西流向河流全年平均流速0.23 m/s,南北流向的直湖港、永安河等河流全年平均流速为0.16 m/s;S1与S6均位于东西向河流上游,水流扰动较强,故藻类浓度最低;而S5断面位于南北向永安河流下游,水动力条件较适合藻类生长,故Chl-a浓度最高。(2) 6个断面Chl-a浓度过程都呈现时间分布不均性,洪季5—10月水动力条件较好,Chl-a浓度相对较低,S1~S6断面洪季平均Chl-a浓度分别为8.15、10.07、9.68、10.57、1103、8.80 mg/m3;而枯季11月至次年4月,水流扰动减弱为藻类生长创造较好环境,Chl-a浓度有所增加,6个断面枯季平均水平分别较洪季增加了9.26%、5.58%、7.42%、6.58%、9.18%、8.09%。S1与S5断面洪枯2季水流差异较大,Chl-a浓度变化最为明显,而S2与S4位于湖口区,Chl-a浓度随季节变化幅度相对较低。(3)6个断面中,S2与S4断面分别位于太滆南运河、直湖港下游入湖口,其Chl-a浓度较其上游S1与S3断面分别增加了28.0%、8.9%;湖泊区水流条件更适宜藻类生长,Chl-a水平整体高于河网区。根据孔繁翔等对大型浅水湖泊中蓝藻水华形成机理的研究结果[21],以Chl-a浓度10 mg/m3作为水华暴发临界值。S1与S6断面Chl-a浓度,除枯季局部时段,基本未达水华暴发水平;S4与S5断面Chl-a浓度则超过了临界值;S2与S3断面Chl-a浓度在临界值附近波动,枯季Chl-a浓度较高时会超过临界水平,而洪季又有所降低。
5 结论
以太湖西北部重污染区的复杂河湖系统为例,针对该区域水系连通发达,水动力条件复杂多变的特征,对水动力影响下的藻类生长过程进行了数值模拟,得到以下结论:(1) 水动力条件的变化会影响藻类生长,适当的动力扰动能促进藻类生长。(2) 提出了水动力影响参数α,对藻类生长公式进行了修正,完善了藻类生长数学模型,从而更合理地对水体富营养化进行模拟和预测。(3)河湖系统内河网区藻类生长与水动力条件关系密切,区内Chl-a浓度呈现显著时空分布不均性。洪季水流扰动较强,Chl-a浓度低于枯季。区内南北向河流的水体流速低于东西向河流,其水动力条件更适宜藻类生长,Chl-a浓度相对较高。研究成果对于区域水华预测预警具有重要指导意义,也为太湖流域解决水体富营养化问题提供了参考。
参考文献:
[1] Lürling M,van Oosterhout F. Controlling eutrophication by combined bloom precipitation and sediment phosphorus inactivation[J]. Water Research,2013,47(17):6527-6537.
[2]Guo L. Doing battle with the green monster of Lake Taihu[J]. Science,2007,317(5842):1166-1166.
[3]逄 勇,丁 玲,高 光. 基于生态槽实验的藻类生长参数确定[J]. 环境科学,2005,26(3):78-82.
[4]张岩松. 北京水系多藻类生态动力学模型[J]. 清华大学学报(自然科学版),2009(12):1992-1996.
[5]Cole F C. Three-dimensional eutrophication model of Chesapeak Bay[J]. Journal of Environmental Engineering,1993,119:1006-1025.
[6]Cerco C F,Noel M R. Twenty-one-year simulation of Chesapeake Bay water quality using the CE-QUAL-ICM eutrophication model[J]. Journal of the American Water Resources Association,2013,49(5):1119-1133.
[7]Nyholm N. A simulation model for phytoplankton growth and nutrient cycling in eutrophic,shallow lakes[J]. Ecological Modelling,1978,4(3):279-310.
[8]郝秀平,王中根. 河湖水系连通分类体系探讨[J]. 自然资源学报,2011(11):1975-1982.
[9]Zhang Y,Zhang Y,Gao Y,et al. Water pollution control technology and strategy for river-lake systems:a case study in Gehu Lake and Taige Canal[J]. Ecotoxicology,2011,20(5):1154-1159.
[10] 马 倩,刘俊杰,高明远. 江苏省入太湖污染量分析(1998—2007年)[J]. 湖泊科学,2010,22(1):29-34.
[11]史小丽,王凤平,蒋丽娟,等. 扰动对外源性磷在模拟水生态系统中迁移的影响[J]. 中国环境科学,2002,22(6):537-541.
[12]章宗涉,刘永定. 微囊藻栅藻资源竞争的动力学过程 Ⅰ. 光能和磷营养的半饱和参数及其生长率动态[J]. 环境科学学报,2000,20(3):349-354.
[13]朱广伟,秦伯强,高 光. 强弱风浪扰动下太湖的营养盐垂向分布特征[J]. 水科学进展,2004,15(6):775-780.
[14]张东生. 河网非恒定流的三级联合解法[J]. 华东水利学院学报,1982,10(1):1-13.
[15]Dewey R J. Application of stochastic dissolved oxygen model[J]. Journal of Environmental Engineering,1984,110(2):412-429.
[16]Zhao D H. Finite-volume two-dimensional unsteady-flow model for river basins[J]. Journal of Hydraulic Engineering,1994,120(7):863-883.
[17]趙棣华,戚 晨,庾维德,等. 平面二维水流-水质有限体积法及黎曼近似解模型[J]. 水科学进展,2000,11(4):368-374.
[18]Zhao D H. Approximate riemann solvers in FVM for 2D hydraulic shock wave modeling[J]. Journal of Hydraulic Engineering,1996,122(12):692-702.
[19]谭维炎. 无结构网格上二维浅水流动的数值模拟[J]. 水科学进展,1995,6(1):1-9.
[20]丁 玲. 水体透明度模型及其在沉水植物恢复中的应用研究[D]. 南京:河海大学,2006.
[21]孔繁翔,高 光. 大型浅水富营养化湖泊中蓝藻水华形成机理的思考[J]. 生态学报,2005,25(3):589-595.endprint

