斯托克斯阻力公式的简单推导
王先智
(上海交通大学物理与天文学院,上海200240)
斯托克斯阻力公式的简单推导
王先智1)
(上海交通大学物理与天文学院,上海200240)
斯托克斯阻力公式的传统推导有些复杂.本文根据线性齐次微分方程所满足的叠加原理提出了一个简单的推导.由于斯托克斯方程是一个二阶线性偏微分方程,根据球表面的两个速度分量条件,方程应该有两个线性独立的和完备的解,这两个解应该构成方程的基本解组,它们的线性组合应该就是方程的通解.使用拉普拉斯方程的解以及量纲分析,找到了这两个解.这两个解的线性组合就是斯托克斯问题的解.
斯托克斯方程,拉普拉斯方程,量纲分析,叠加原理
流体力学里最重要的问题之一就是斯托克斯问题[1],即确定在无限大的不可压缩流体里作缓慢的匀速直线运动的一个刚球所受到的阻力.据我们所知,存在3种解法.第1种解法就是斯托克斯流函数法[13],即首先推导斯托克斯流函数所满足的方程,然后求解该方程.第2种解法就是球谐函数展开法[2].第3种解法就是矢量势法[4],即利用不可压缩流体的连续性方程,把流体速度表示为矢量势的旋度.我们在流体力学本科教学中注意到,本科生对这三种推导的理解比较困难,因此有必要发展一种简单的解法[59].本文根据线性齐次微分方程所满足的叠加原理提出了一个简单的线性叠加解法.
对于不可压缩流体的定常流动,纳维--斯托克斯方程为

式中ρ为流体密度,η为剪切黏滞系数.连续性方程为

在球缓慢运动的情况下,可以略去纳维--斯托克斯方程中的惯性项,方程成为线性方程(称为斯托克斯方程),即

取方程(3)的散度,并使用连续性方程(2),我们发现压强满足拉普拉斯方程,即

取方程(3)的旋度,我们发现涡量Ω=∇×v满足拉普拉斯方程,即

使用球坐标 (r,θ,ϕ). 把原点取在球心的瞬时位置上,z轴平行于球的速度,即 U = Uez=U(ercosθ−eθsinθ). 这里 ez,er和 eθ是单位矢量.由于斯托克斯流动是轴对称流动,流体速度和压强可以分别表示为 v=ervr(r,θ)+eθvθ(r,θ),P=P(r,θ).因此连续性方程∇·v=0化简为
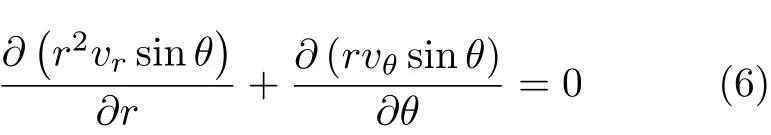
从上式可以定义斯托克斯流函数ψ(r,θ),流体速度可以表示为

边界条件为
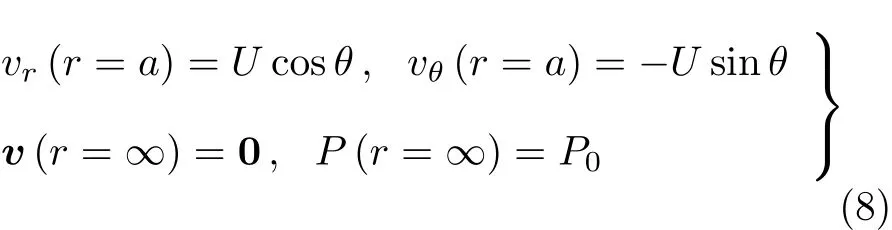
式中a为球的半径,P0为常数.
把方程(7)代入条件(8)得
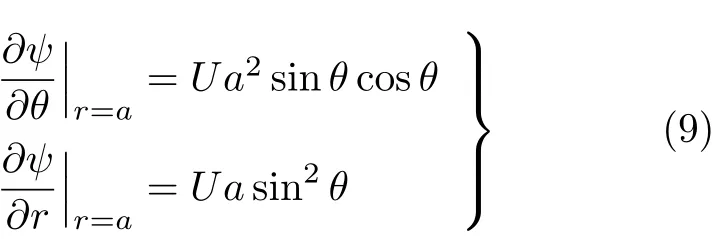
上式建议了斯托克斯流函数可能的形式

式中f(r)为一个待定函数.
现在我们使用线性齐次微分方程所满足的叠加原理来求解斯托克斯问题.任何线性齐次微分方程都满足叠加原理[9],即任何线性齐次微分方程的任意数目的解的任意线性组合都是方程的解.为了得到一些具体线索,我们首先回忆一下齐次线性常微分方程理论[10].n阶齐次线性常微分方程定义为

可以证明,n个初始条件导致解的存在与唯一性定理,以及n阶线性齐次常微分方程有n个线性独立的和完备的解,它们构成方程的基本解组,它们的任意线性组合都是方程的通解.满足n个初始条件的通解是唯一的[10].
现在回到斯托克斯问题.既然n个初始条件导致n阶线性齐次常微分方程有n个线性独立的和完备的解,而斯托克斯方程是一个二阶线性偏微分方程,在球表面的边界条件为 vr(r=a)=U cosθ和vθ(r=a)= −U sinθ,那么根据球表面的这两个速度分量条件,我们期望斯托克斯方程应该有两个线性独立的和完备的解,这两个解应该构成方程的基本解组,它们的线性组合应该就是方程的通解并且应该满足球表面的两个速度分量条件.
现在我们来寻找斯托克斯方程的两个线性独立的和完备的解.当然,这两个解需要满足无限远处的速度条件和压力条件,但不满足球表面的两个速度分量条件.
从方程 (5),我们马上发现,无旋流动 Ω =∇×v=0是斯托克斯方程(3)的一个解.众所周知[24],无旋流动由速度势Φ所确定,流体速度为v=∇Φ.速度势满足拉普拉斯方程,即

在这种情况下,斯托克斯方程(3)化简为∇P=0,解为P=const.无旋流动解对流体压强只不过贡献了一个常数.
拉普拉斯方程∇2Φ=0的解为
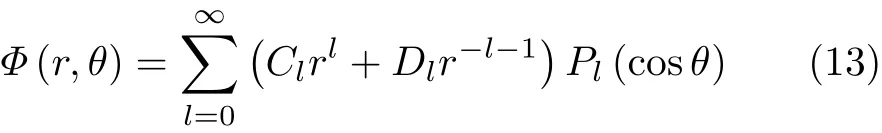
式中Pl(cosθ)为勒让德多项式,有P0(cosθ)=1和P1(cosθ)=cosθ,Cl和 Dl为常数.
由球表面的边界条件 vr(r=a) = U cosθ和 vθ(r=a)= −U sinθ可知,速度势 Φ 只与P1(cosθ)=cosθ有关,即
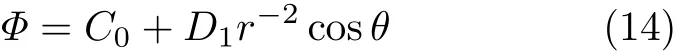
相应的流体速度和斯托克斯流函数分别为
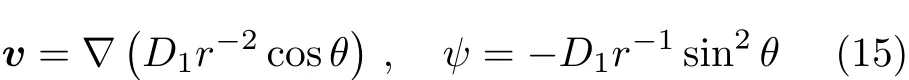
现在我们寻找另一个解.拉普拉斯方程∇2P=0的解为

式中Al和Bl为常数.
由球表面的边界条件 vr(r=a)=U cosθ和vθ(r=a)=−U sinθ以及斯托克斯方程(3)可知,压强P 只与P1(cosθ)=cosθ有关,即
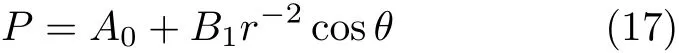
把方程(17)代入式(3)得
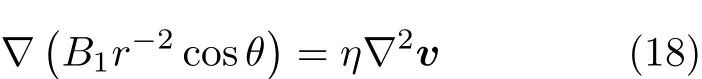
现在使用量纲分析来获得一个解.我们注意到,r是一个有量纲的变量,而 θ是一个无量纲的变量,所以取r为基本量,而把其他物理量取为导出量[11].令 v和 ψ的量纲分别为 [v]=rβ和[ψ]=rα.这里 β 和 α 为待定常数.使用 [∇]=r−1和 [∇2]=r−2,我们获得

上式给出β=−1.使用方程(7)得

上式给出α=2+β=1.参考方程(10),我们获得
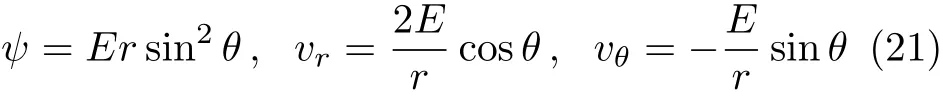
式中E为待定常数.
现在我们证明,式 (21)的确是方程(18)的解.把式(21)代入方程(18)的径向分量方程
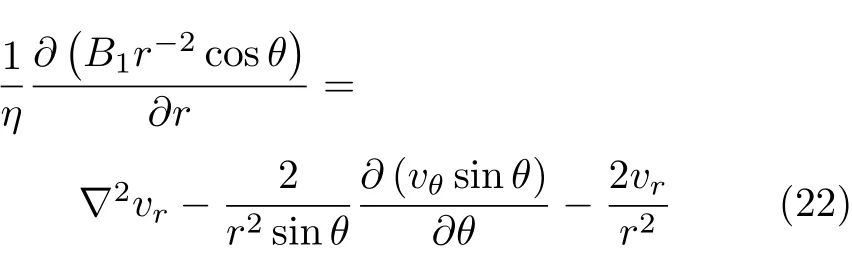
然后经过简单计算,我们获得

上面我们得到的斯托克斯方程的两个解之一是无旋流动解,其斯托克斯流函数ψ=−D1r−1sin2θ反比于r,另一个量纲分析解是有旋流动解,其斯托克斯流函数ψ=Ersin2θ正比于r,这两个斯托克斯流函数的比值不是常数,因此这两个解是线性独立的[10].所以这两个解的线性组合就是斯托克斯方程的通解,即

式中的两个待定常数 E和 D1由边界条件 (8)确定,即

应力张量计算如下
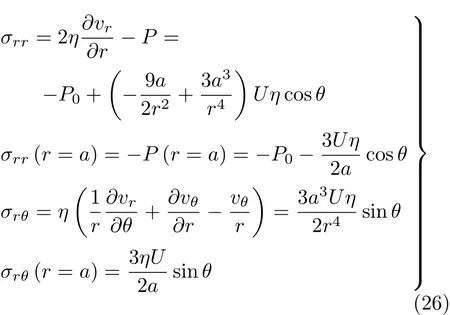
把球表面上的所有面元所受到的力加起来就得到阻力,即

综上所述,斯托克斯阻力公式的传统推导有些复杂.本文根据线性齐次微分方程所满足的叠加原理提出了一个简单的推导.既然 n个初始条件导致n阶线性齐次常微分方程有n个线性独立的和完备的解,而斯托克斯方程是一个二阶线性偏微分方程,根据球表面的两个速度分量条件,我们期望方程应该有两个线性独立的和完备的解,这两个解应该构成方程的基本解组,它们的线性组合应该就是方程的通解.使用拉普拉斯方程的解以及量纲分析,我们找到了这两个解,这两个解的线性组合就是斯托克斯问题的解.
1 Stokes GG.On the effect of the internal friction of fluids on the motion of pendulums.Transaction of the Cambridge Philosophical Society,1851,9:8-106
2 Lamb H.Hydrodynamics.New York:Dover,1945
3 Milne-Thomsonm LM.Theoretical Hydrodynamics.London:MacMillan,1955
4 Landau LD,Lifshitz EM.Fluid Mechanics. London:Butter worth-Heinmann,1998
5姜楠.一个重要的流体力学基本概念.力学与实践,2015,37(1):119-12
6陈庆光,张明辉,朱绪力等.流体力学课程教学中几个基本概念的教学方法.力学与实践,2015,37(1):138-141
7赵军方.关于流体力学中的几个基本概念的再解读.力学与实践,2017,39(3):296-298
8赵军方,孙晓芳.用微元六面体推导流体力学基本方程时参考点的选择.力学与实践,2016,38(6):676-678
9柯朗R,希尔伯特 D.数学物理方法,第一卷.北京:科学出版社,1977
10四川大学数学系高等数学教研室.高等数学,第三册第二分册.北京:人民教育出版社,1979
11 Kay JM,Nedderman RM.Fluid Mechanics and Transfer Processes.London:Cambridge,1985
O357
A
10.6052/1000-0879-17-169
2017–05–22收到第1稿,2017–08–01 收到修改稿.
1)王先智,教授,主要研究方向为统计物理.E-mail:xzwang@sjtu.edu.cn
王先智.斯托克斯阻力公式的简单推导.力学与实践,2017,39(6):617-619
Wang Xianzhi.A simple derivation of the Stokes formula of the drag.Mechanics in Engineering,2017,39(6):617-619
(责任编辑:周冬冬)

