MMC-HVDC互联系统协调控制策略与频率响应分析
,, ,兴源,
(四川大学电气信息学院,四川 成都 610065)
MMC-HVDC互联系统协调控制策略与频率响应分析
杨林,张英敏,李丹,李兴源,刘天琪
(四川大学电气信息学院,四川 成都 610065)
模块化多电平换流器(modular multilevel converter,MMC)型直流输电技术是近年来新能源集中送出和远距离异步联网较好的解决方案。负荷变化通过直流电网对交流系统产生的频率响应是一个重点研究课题。研究了基于模块化多电平换流器的多端柔性直流输电(modular multilevel converter based multi-terminal high voltage direct current,MMC-MTDC)系统的协调控制策略,通过交流电网的频率下垂控制和MMC换流站的直流电压下垂控制实现瞬时功率的平衡。通过引入换流站附加频率控制策略,使某个换流站交流系统出现负荷-频率变化时其他交流系统可以通过直流电网参与功率和频率调整,并进行理论推导频率响应关系,得出频率响应矩阵。在PSCADX4/EMTDC仿真软件搭建四端直流电网模型进行验证,结果表明控制策略的有效性与频率响应分析的可行性。
MMC-MTDC;互联系统;协调控制;电压下垂控制;频率响应
0 引 言
基于电压源换流器的高压直流输电技术在新能源集中送出和全球能源互联等方面具有明显优势[1-4]。多端直流和直流电网能够实现大容量传输,对换流站所连交流系统实现无功支撑,不同交流系统之间实现频率解耦和连接不同刚性强度的交流系统[5]。基于电压源换流器的多端直流系统或者直流电网系统的相关技术还未完全成熟,很多相关技术需要在装备工程前进行攻关。其中一个核心问题是如何决定换流站的运行条件(如直流电压、电压下垂和频率下垂等)和在交直流故障情况下的电压穿越能力。为了决定换流站频率下垂的调节能力,有必要研究换流站交流侧负荷变化引起其他换流站交流侧频率变化以及换流站传输功率变化的数学关系。
目前文献研究侧重于多端直流电网的直流电压下垂控制策略和附加频率控制策略,鲜有文献研究直流电网的交流侧频率响应和稳定问题。文献[6]研究了直流电压下垂控制策略,能够对直流网络的潮流做出快速的响应,改善主导换流站容易满载的情况,但该策略不能对功率进行精确控制。文献[7]研究了多端直流系统的电压下垂控制策略,并在此基础上引入附加频率控制,实现了互联系统的频率稳定控制,但是该文没有研究各个换流站之间的频率、功率和电压之间的变化关系。电网频率是发电有功功率与负荷之间的关系,是电力系统稳定控制的重要参数[5,8]。交流系统通过MMC-MTDC实现互联时,由于换流站对有功无功采用解耦控制,使得直流侧功率对交流系统频率不敏感,有隔绝交流侧系统相互影响的优势,但失去了在交流侧发生故障时的频率相互紧急支援能力。利用直流系统对交流侧电网进行频率辅助控制和事故时换流站相互紧急功率支援,能够提高交直流电网的安全稳定性和实现区域间能源互补[9-10]。
为了使互联交流系统在发生事故时能够功率相互支撑,研究了适用于MMC-MTDC互联系统的协调控制策略。该控制策略集交流电网频率下垂控制、直流电压下垂控制以及换流站频率下垂控制于一体,在一端换流站交流电网频率变化较大时,具有调频能力的交流电网通过直流电网实现功率支援,减少故障端系统频率变化量。通过研究直流电压变化量、功率变化量和频率变化量之间的数学关系,得出频率响应矩阵。最后通过PSCADX4/EMTDC进行仿真验证,仿真结果符合所提协调控制策略和频率响应分析。
1 MMC-HVDC互联系统
基于模块化多电平换流器的多端直流输电系统如图1所示。图中:G1、G2、G3、G4分别表示交流系统中的发电机组;Load1、Load2、Load3、Load4表示交流系统的负荷;MMC1、MMC2、MMC3、MMC4表示四端换流站;直流互联系统搭建成张北四端换流站的口字型直流电网结构[1,11-12]。
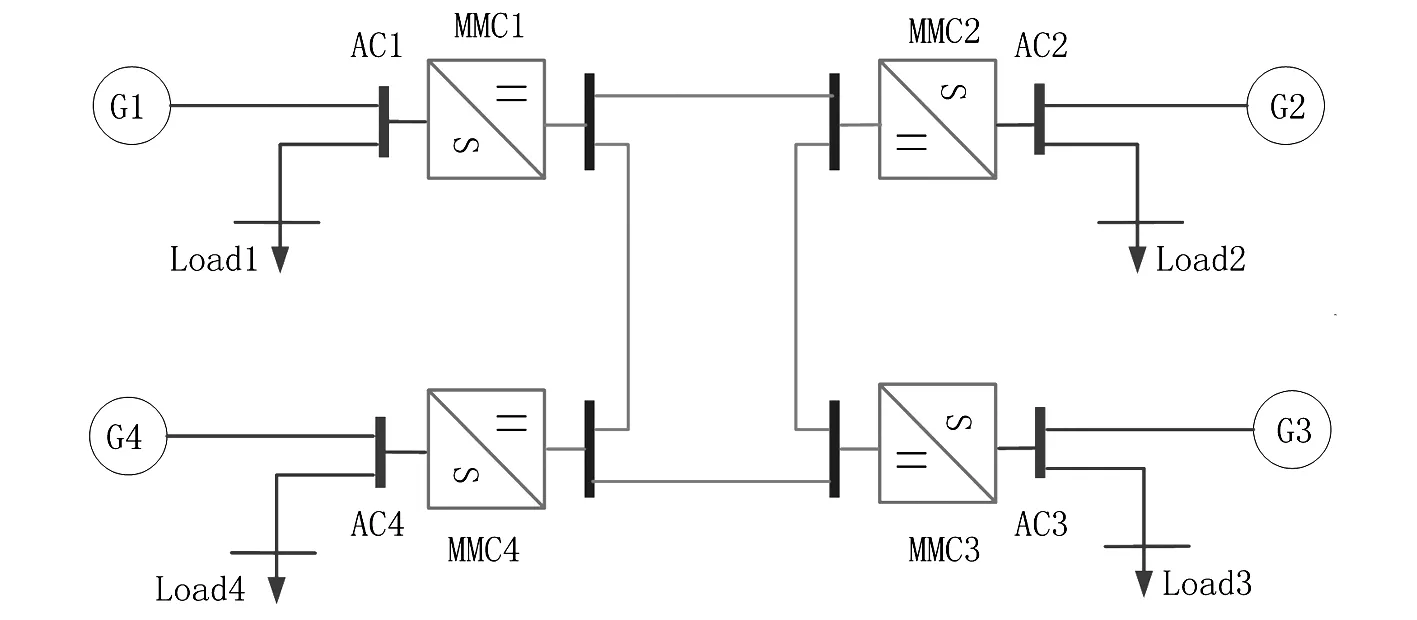
图1 MMC-MTDC系统结构
2 MMC的数学模型与控制结构
2.1 MMC的数学模型
MMC的简化单线图如图2所示。PCC点为换流站与交流系统的公共耦合点,L和R分别代表等值电抗和等值电阻,在数学模型分析中忽略半导体的损耗。

图2 MMC简化单线图
运用同步旋转坐标系对MMC的数学模型进行分析,在图2所示的MMC单线图中,流过阻抗的电流满足式(1)方程:
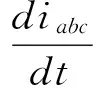
(1)
式中,Usabc、Ucabc、iabc分别为PCC点三相电压、换流器端口三相电压和换流器端口三相电流。
为了便于实现换流器的控制,将三相参考系下的参量转换到两相同步旋转参考坐标系(d-q坐标系)。式(1)在d-q坐标系下转换为[13]
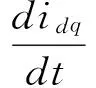
(2)
在控制系统中,d-q变换中的角度是利用锁相环(PLL)追踪PCC点稳态三相坐标系中A相的电压相位角度。当以d轴定向时,Usq=0和Usd=Us。将式(2)简化为
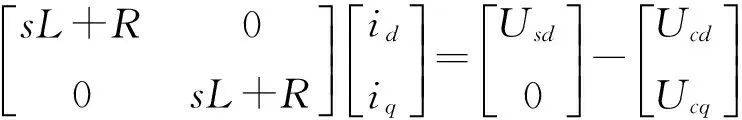
(3)
交直流侧电压满足式(4):
(4)
式中,[md,mq]为d-q坐标系下交流电压的调制系数。联立式(3)和式(4),得到:
(5)
式(5)表示了MMC在线性运行区域的数学模型,该模型的参数用于电流内环的PI控制环节。
2.2 MMC的控制结构
MMC换流站的控制策略是基于同步旋转坐标系进行设计的,控制器中的内环电流控制器包括有功分量和无功分量。为了适应各种运行模式,外环电压控制器中有功分量包括直流电压、有功功率或者频率,无功分量包括交流电压或无功功率,如图3和图4所示。
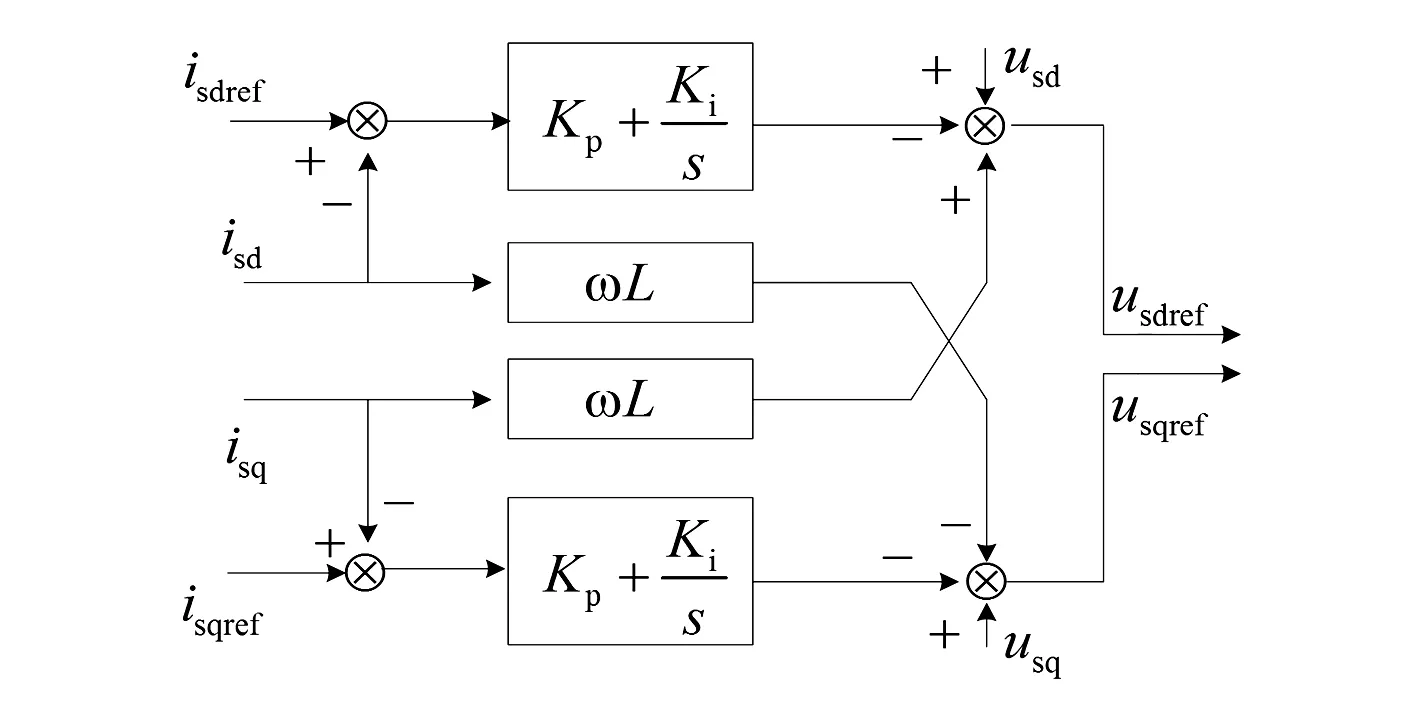
图3 内环电流控制环节
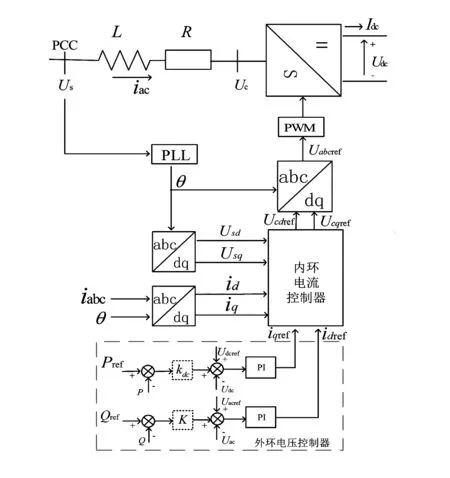
图4 包含外环控制器的完整MMC控制结构
图4为包含外环控制器的完整MMC控制结构。换流器的有功分量可以采用控制直流电压,有功功率或者两者同时控制的直流电压下垂控制。表示直流电压下垂控制中的下垂系数,其大小影响着换流站之间功率传输的大小。功率流进换流器的方向为正方向。同样,换流器的无功分量可以采用控制无功功率,公共耦合点的交流电压或者两者同时控制的无功下垂控制。
3 MMC-MTDC互联系统控制策略
3.1 交流电网频率下垂控制
交流电网的频率下垂控制是所有交流电网稳定运行主要控制方式,发电机组和负荷之间功率暂态平衡通过频率变化来反应。交流电网的一次频率调整是通过主调频发电厂调速器的频率下垂控制模块实现的,其控制机制是将频率作为全局变量来平衡交流电网的功率交换。频率下垂控制的控制结构如图5所示,其详细的下垂特性和结构参考文献[5,14]。
频率下垂系数ρac的大小表示发电机在交流电网功率不平衡导致频率偏移时的补偿能力。在图5中,频率下垂系数越小,交流系统就越强。典型的频率下垂系数为0.04~0.08 pu。
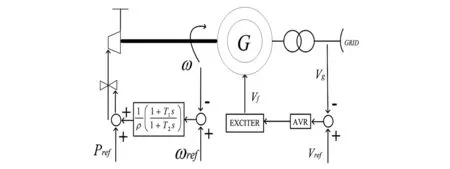
图5 发电机组频率下垂控制
3.2 直流电压下垂控制
在直流电网中,若单一换流站承担直流网络的不平衡功率,可能会导致与换流站连接交流系统的频率发生较大的变化。为使具备系统功率调整的换流站参与直流网络的不平衡功率的调整,换流站应工作在平衡节点的状态。直流电压下垂控制策略来源于交流系统的调频控制思想,其控制方式可以采用一条直流电压和功率的关系曲线来表示,控制器特性和控制器结构如图6所示[15]。图中,Udcref为直流电压参考值,Pref为有功功率参考值,kdc为直流电压下垂系数。
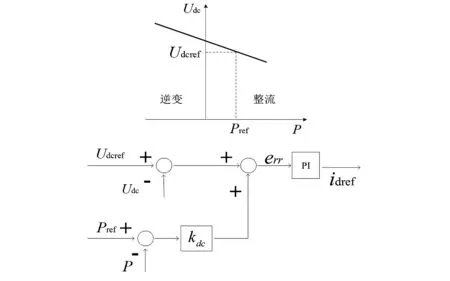
图6 直流电压下垂控制器
直流电压下垂控制结合了功率控制和直流电压控制的特点,其目的在于实现直流网络的功率平衡。err为直流电压的偏差量,在稳态工作点时可近似为0。图6中直流电压和直流功率之间的关系为
Udc=Udcref+kdc(Pref-P)
式中,kdc决定了每个换流站分担直流网络中不平衡功率的大小,较小的值意味着该换流站承担较多的不平衡功率。直流电压下垂控制策略不需要换流站间通信,不用切换换流站的控制模式,具备功率调节的换流站根据其所测得的直流电压按固定的斜率调整至功率指定值,来承担网络不平衡功率。
3.3 附加频率控制
采用直流电压下垂控制策略的换流站参与直流网络不平衡功率的调整,减缓单个主导换流站所连交流系统承受的冲击。采用前面讨论的直流电压下垂控制策略时,换流站不能对交流系统频率做出响应,使得其他换流站不能通过MTDC进行功率支援,交流系统的频率只能取决于本地发电机组的调频能力和负荷的功频特性,不能充分利用整个互联系统的频率调整能力。
为了使具有调频能力的交流系统通过MMC-MTDC系统实现互联系统频率协调控制,在电压下垂控制器中引入频率下垂控制,如图7所示。
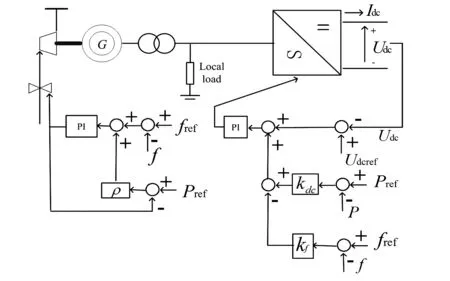
图7 MMC换流站的频率控制
3.4 MTDC的频率响应分析
图7中可以看出,换流站的有功功率的变化与直流电压的偏移和交流电网的频率偏移相关。直流电压下垂系数表示电压变化量与功率变化量之比,频率下垂系数表示电压变化量与频率变化量之比。为了研究交直流互联电网的频率响应,这里定义每个换流站的交直流侧的参数如图8所示。
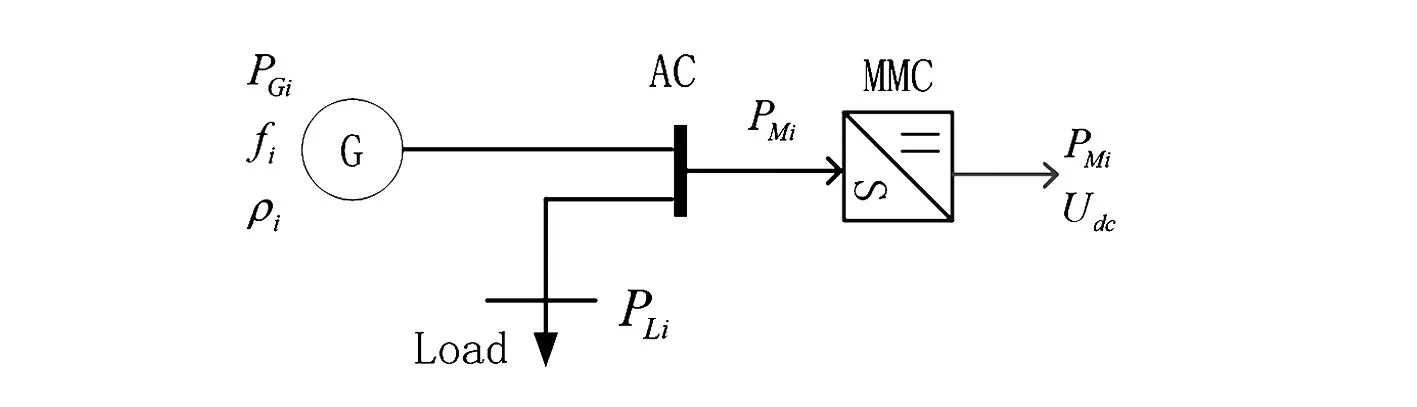
图8 交直流侧参数的定义
图8中的交流系统以集中模型来表示,图7、图8中的参数定义如下:
PMi为交流系统向MTDC传输的功率,GW;PLi为当地负荷,GW;PGi为交流系统集中发电容量,GW;fi为系统频率,Hz;Udc为直流电压,kV;ρi为集中交流系统频率下垂系数;kdc为换流站直流电压下垂系数;kf为换流站频率下垂系数。
在直流电网中,由于线路电阻很小,所以假设不同换流站直流侧端口直流电压相等。从图8的控制结构可以看出,交流系统功率的平衡关系满足如式(6)的方程:
ΔPLi+ΔPMi=ΔPGi
(6)
式中,ΔPLi、ΔPMi、ΔPGi分别为当地负荷变化量、换流站MMC功率变化量、发电机功率变化量。交流系统频率下垂特性与发电功率变化的关系为
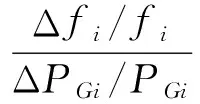
(7)
在图7中的控制策略可以得出:
ε=Udcref-Udc+kdc(Pref-P)-kf(fref-f)
(8)
当系统稳态运行时,ε=0。则交流频率的变化和(或者)直流母线电压的变化导致的功率变化量为
(9)
当忽略直流系统的损耗时,MTDC的换流站不会产生,也不会消耗功率,所有换流站交换功率的变化量等于0。
(10)
对于n个换流站,则有
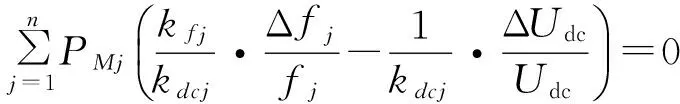
(11)
联立式(6)、式(7)、式(9)和式(11),可得负荷功率变换为
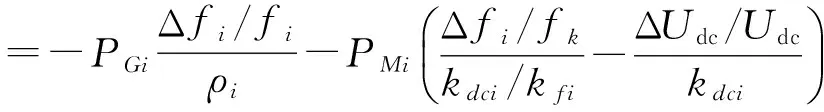
(12)
将式(12)简记为
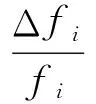
(13)
式中,
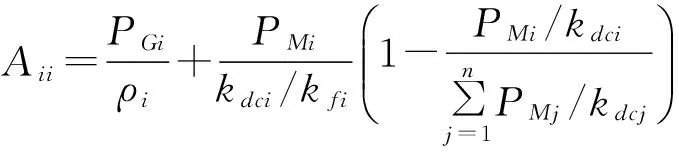
将式(13)改写成矩阵形式
(14)
式(14)表示了直流电网的交流侧负荷与频率变化的关系,式中变量上方加“-”为变量的标幺值。将矩阵的主对角元素Aii定义为换流站的频率自响应因子,定义非对角元素Aij为换流站之间的频率互响应因子。频率自响应因子反应了第i个换流站交流侧负荷变化引起的频率偏移的强度,频率互响应因子反应了第i个换流站交流侧负荷变化引起第j个换流站交流侧频率偏移的强度。在式(12)分析可知,式(14)中矩阵元素由换流站控制器的参数、交流电网的下垂系数、发电机组发出的功率和换流站交换的功率来决定的,将该矩阵称之为频率响应矩阵。交流系统负荷变化量通过式(14)即可求出参与频率调节的交流电网的频率偏移。将方程(11)改写为如下矩阵形式:
(15)
图7中交直流参数全部给定后,通过式(14)和式(15)求出频率和直流电压的变化量,可以快速地确定各个换流站潮流的变化和参与交流电网调频的强度。
4 仿真验证
为了验证所研究的互联系统协调控制策略和频率响应分析方法,在PSCADX4/EMTDC仿真软件中搭建基于模块化多电平换流器的四端直流电网。交流网络利用水轮发电机和当地负荷进行等值。直流电网的换流站都采用所研究的基于附加频率控制的直流电压下垂控制策略。仿真中的所有控制参数设定如表1所示。
根据表1得出
(16)
(17)
在本仿真模型中,在换流站MMC1的交流电网增加1.5 GW的额外负荷。将ΔPL1=1.5 GW,代入式(16)和式(17),可得理论计算下的电压偏移、换流站功率偏移和频率偏移,其中ΔPL2=ΔPL3=ΔPL4=0 GW。
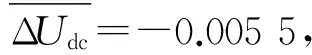
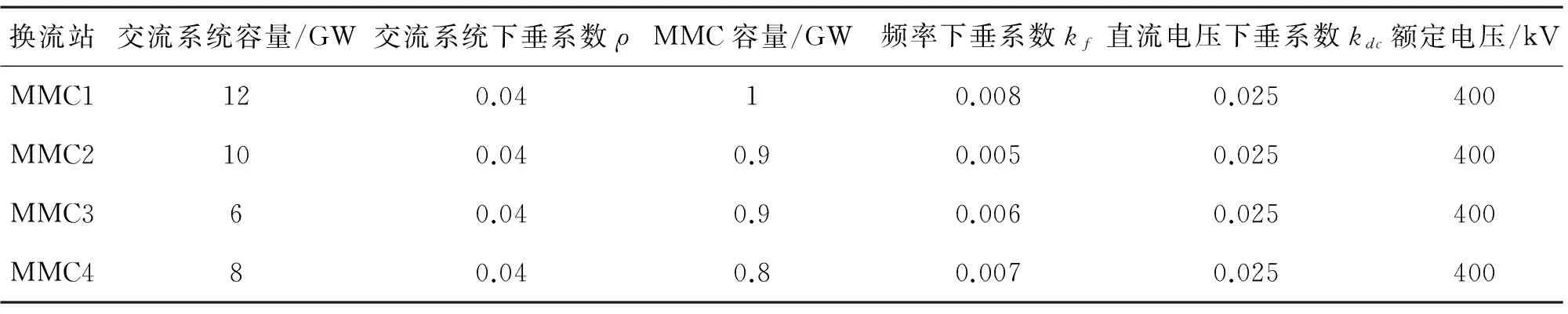
表1 仿真系统参数
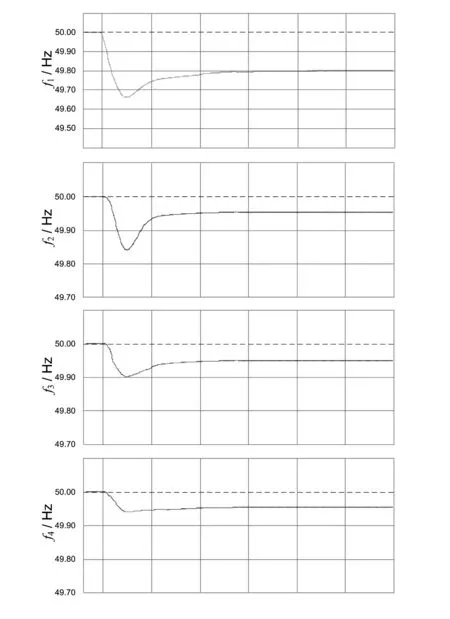
图9 频率响应仿真结果
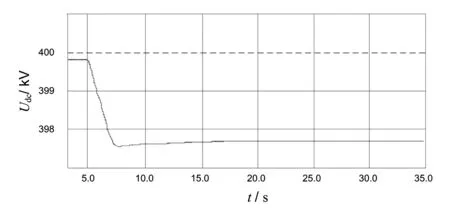
图10 直流电压响应仿真结果

ΔUdc=-0.0050p.u.ΔPM1=-0.300GWΔf1=-0.0040p.u.ΔPM2=0.108GWΔf2=-0.0004p.u.ΔPM3=0.090GWΔf3=-0.0006p.u.ΔPM4=0.102GWΔf4=-0.0005p.u.

表3 相关物理量的仿真结果
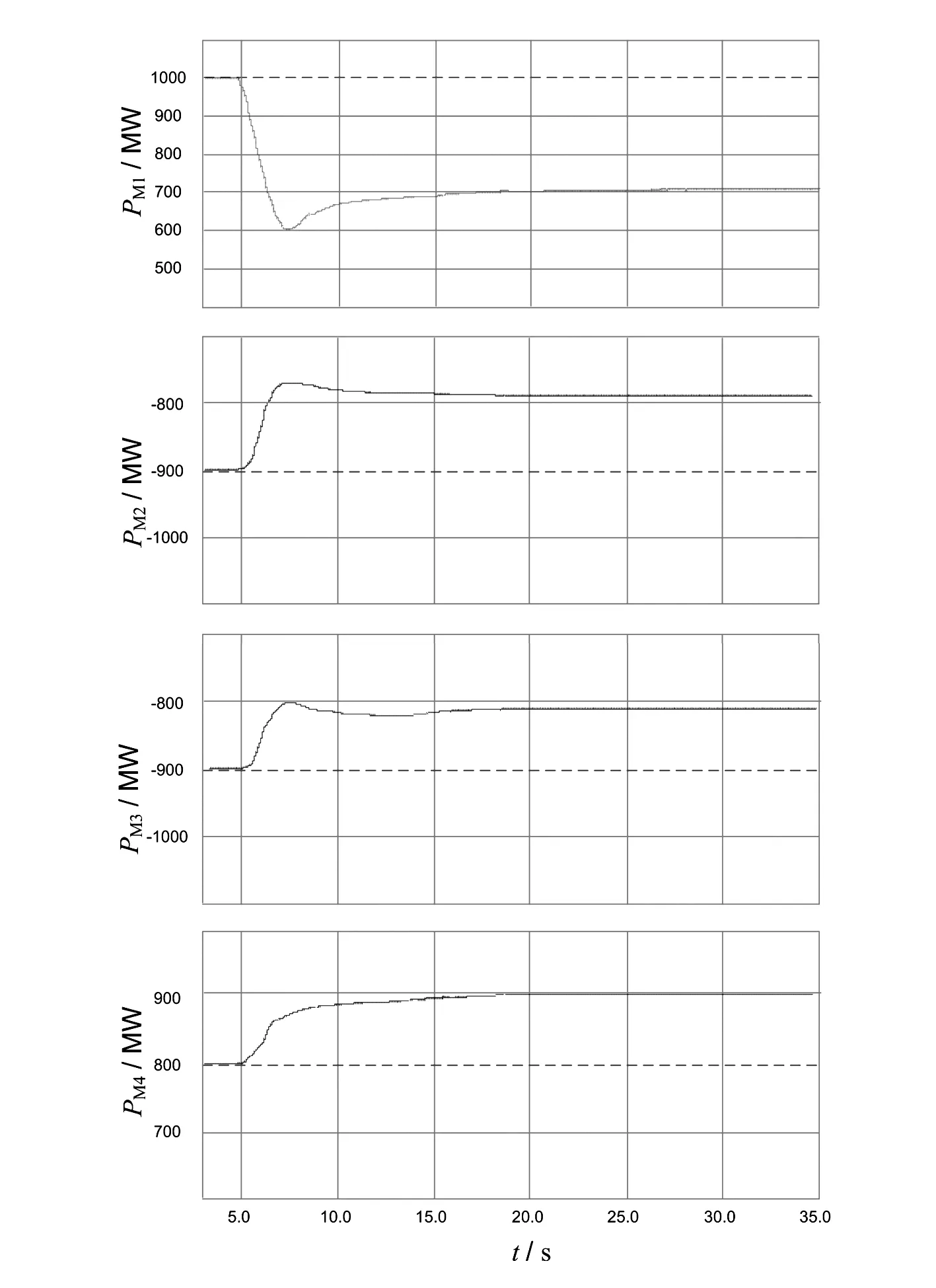
图11 功率响应仿真结果
5 结 语
研究了基于MMC-MTDC互联直流电网的协调控制策略和频率响应分析方法。该协调控制策略无需站间通信,通过在换流站控制器中加入附加频率控制策略,使有调频能力的交流电网参与故障交流电网的频率响应,并使换流站共同分担直流电网的不平衡功率。前面研究的是各个换流站交流系统频率的响应,下一步的工作将对交流网络频率偏移范围、系统的刚性强度、换流站的允许容量范围与满载情况、直流电压等级,以及控制器参数等相关参量之间的相互影响进行研究。
[1] 汤广福,庞辉, 贺之渊.先进交直流输电技术在中国的发展与应用[J].中国电机工程学报,2016,36(7):1760-1771.
[2] 汤广福,罗湘, 魏晓光.多端直流输电与直流电网技术[J].中国电机工程学报,2013,33(10):8-17.
[3] Rouzbehi K, Miranian A, Luna A, etal.DC Voltage Control and Power Sharing in Multiterminal DC Grids Based on Optimal DC Power Flow and Voltage-droop Strategy[J].Emerging & Selected Topics in Power Electronics of IEEE Journal,2014,2(4):171-1180.[4] Xu L,Williams B W, Yao L.Multi-terminal DC Transmission Systems for Connecting Large Offshore Wind Farms[C]// Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the Century IEEE,2008:1-7.
[5] Prahba Kundur.Power System Stability and Control[M].TataMcGraw-Hill,1994:396.
[6] 陈谦,唐国庆, 潘诗锋. 采用多点直流电压控制方式的VSC多端直流输电系统[J].电力自动化设备, 2004, 24(5):10-14.
[7] 朱瑞可,李兴源,应大力. VSC-MTDC互联系统频率稳定控制策略[J].电网技术, 2014,38(10):2729-2734.
[8] 程丽敏, 李兴源.多区域交直流互联系统的频率稳定控制[J].电力系统保护与控制,2011,39(7):56-62.
[9] 姚良忠,吴婧,鲁宗相,等. 含大规模风电场接入的多端直流系统对交流系统频率调节的作用[J].高电压技术, 2016,42(10):3038-3044.
[10] 凌卫家,孙维真,张静,等.舟山多端柔性直流输电示范工程典型运行方式分析[J].电网技术,2016,40(6):1751-1758.
[11] 王艳婷,张保会,范新凯. 柔性直流电网架空线路快速保护方案[J].电力系统自动化,2016, 40(21):13-19.
[12] 韩亮,白小会,陈波,等.张北±500kV柔性直流电网换流站控制保护系统设计[J].电力建设,2017,38(3):42-47.
[13] Haileselassie T M, Molinas M, Undeland T.Multi-terminal VSC-HVDC System for Integration of Offshore Wind Farms and Green Electrification of Platforms in the North Sea[C].Proceedings of the Nordic Workshop on Power & Industrial Electronics, 2008.
[14] Jan Machowski, Janusz W. Bialek, Jams R. Bumby.Power System Dynamics and Stability[M].John Wiley & Sons,1997:327.
[15] 徐政.柔性直流输电系统[M].北京:机械工业出版社,2013.
Modular multilevel converter based HVDC technology is a good solution to the centralized dispatch of new energy sources and remote asynchronous interconnection in recent years. The response of load /frequency variation to the AC system through the DC power grid is a key research topic. The coordinated control strategy of multi-terminal flexible DC transmission system based on modular multilevel converter (MMC-MTDC) is studied, which realizes the balance of instantaneous power by means of frequency droop control of AC power grid and DC voltage droop control of MMC converter station. By introducing the additional frequency control strategy of converter station, the AC system can be used to participate in the power and frequency response through the DC power grid when the load frequency changes in the AC system of a converter station, and the frequency response matrix is obtained by theoretical derivation. The simulation results show that the effectiveness of control strategy and the feasibility of frequency response analysis are verified by the four terminal DC power grid model with PSCADX4/EMTDC simulation software.
MMC-MTDC; interconnected system; coordinated control; voltage droop control; frequency response
TM721
A
1003-6954(2017)06-0001-06
国家重点研发项目(2016YFB0900901)
杨 林(1991),硕士研究生,主要研究方向为电力系统稳定与控制、柔性直流输电技术;
张英敏(1974),博士、副教授、硕导,主要研究方向为电力系统稳定与控制、高压直流输电等;
李 丹(1987),硕士研究生,主要研究方向为电力电子、柔性直流输电技术;
李兴源(1945),教授、博导、IEEE高级会员,主要研究方向为电力系统稳定与控制、高压直流输电、分布式发电;
刘天琪(1962),博士、教授、博导,主要研究方向为电力系统稳定与控制、高压直流输电。
2017-08-01)

