离合器从动盘性能对汽车耸车的影响

刘雪莱， 上官文斌， 李 林， 侯秋丰， 王善南

(1.华南理工大学机械与汽车工程学院 广州，510641) (2．广东轻工职业技术学院汽车技术学院 广州，510300) (3.宁波宏协股份有限公司 宁波，315807)

离合器从动盘性能对汽车耸车的影响

刘雪莱1， 上官文斌1， 李 林2， 侯秋丰3， 王善南3

(1.华南理工大学机械与汽车工程学院 广州，510641) (2．广东轻工职业技术学院汽车技术学院 广州，510300) (3.宁波宏协股份有限公司 宁波，315807)

为了研究离合器从动盘性能对汽车耸车振动的影响，建立了传动系统-汽车整车的11自由度非线性动力学模型。模型考虑了离合器从动盘的扭转特性、干摩擦阻尼、离合器接合黏滑特性以及变速器轮齿啮合刚度。利用建立的模型计算汽车起步过程系统动力学响应，通过实车测试验证模型的正确性，分析离合器从动盘性能参数对耸车振动的影响。结果表明：汽车的耸车现象发生在离合器完全接合之后；耸车振动频率与传动系第2阶固有频率相近；提高静摩擦因数，降低从动盘转动惯量和2级扭转刚度，可以降低汽车在起步过程中的耸车振动。本研究的建模和分析方法，可以用来计算与分析离合器从动盘结构性能参数对整车耸车振动特性的影响。

离合器从动盘； 建模与仿真； 参数分析； 耸车； 实车测试

引 言

耸车现象是指在汽车起步过程中，车辆以较低的频率在行驶方向上前、后振荡。产生耸车的原因有：a.汽车起步、离合器接合，传动系统的固有频率与发动机的激励频率接近而产生的振动；b.由于离合器在结合过程中，离合器的主动部分和从动部分是摩擦传动，由于摩擦因数与相对滑移速度的关系可能是负梯度，这样摩擦过程中，会产生自激振动，从而引起耸车；c.由于发动机输出转矩的波动，导致动力总成的抖动，从而引起整车的耸车。耸车振动的频率一般在2～8 Hz范围内[1-3]，它严重影响了汽车传动系统振动噪声性能(noise vibration harshness,简称NVH)。对于安装有干式摩擦离合器的汽车来说，在起步过程中，离合器接合速度快，传动系统负载变化快，接合产生的冲击较大，因此，耸车振动现象尤为严重。

对起步振动的研究中，目前主要放在对变速箱敲齿和传动系高频振动的研究上，对于耸车的研究较少。文献[4-6]在对汽车传动系统扭转振动研究的过程中发现，离合器的突然接合，发动机节气门开度的突然变化，会导致传动系统发生低频的刚体扭转振动，产生耸车现象。Centea等[7]在用集总参数法对汽车传动系统进行建模研究汽车起步抖动，也发现了在离合器接合完成后，传动系统会发生低频的扭转振动现象。任少云等[8-9]建立了汽车传动系统动力学模型对耸车现象进行研究，并对比分析了传动系一些关键参数变化对耸车的影响。Crowther等[10]在对汽车起步过程进行计算分析中，将离合器分成黏、滑两个状态，并利用Karnopp模型来对离合器的黏、滑状态进行建模。Couderc等[11]在考虑齿轮啮合间隙以及离合器从动盘扭转特性的基础上对传动系进行建模，并对传动系统进行了模态分析。文献[12-13]在考虑干摩擦阻尼的情况下，给出了离合器从动盘扭转特性的建模方法。以上工作对研究分析耸车问题提供了有效的建模思路。

为了降低汽车在起步过程中的耸车振动，建立了包括离合器、变速器等在内的传动系统11自由度模型。模型中包含离合器从动盘的扭转特性摩擦阻尼、离合器在接合过程中的黏、滑两种状态及变速器轮齿啮合刚度。利用建立的动力学模型，计算分析了汽车起步过程传动系统与整车的响应，并通过实车试验，验证模型与计算结果的一致性。基于优化离合器从动盘的性能参数以减少起步过程中耸车，分析离合器从动盘性能参数对耸车振动的影响，结果表明，汽车的耸车振动现象出现在离合器接合后，耸车振动与传动系第2阶固有频率相近。通过提高静摩擦因数，降低从动盘转动惯量和2级扭转刚度，可以降低汽车在起步过程中的耸车振动。本研究的建模和分析方法，可以用来计算与分析离合器从动盘结构性能参数对整车耸车振动特性的影响。

1 汽车传动系统动力学建模

1.1 动力学模型

笔者所研究的耸车振动，实际是由于离合器接合产生冲击，整个传动系统产生的低频扭转振动。因此，建立包括车身在内的整车传动系统11自由度动力学模型，如图1所示。由于所研究的是传动系扭转振动以及车身的纵向振动，为了能反映出振动现象，忽略整个传动系各部件的阻尼，仅考虑发动机离合器扭转减振器阻尼和轮胎与地面间的阻尼。模型中的参数含义以及数值见表1。

利用牛顿第二定律得出图1建立的动力学模型的数学方程，并以矩阵的形式写出

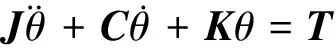
(1)

其中：J为系统惯量矩阵，是关于J1，J2，…，J11的函数矩阵；C为系统阻尼矩阵，是关于C1，C2的函数矩阵；K为系统刚度矩阵，是关于K1，K2，…，K10的函数矩阵；T为系统力矩向量。

T的表达式为

T=[Te-TcTc-TmTm

-TgTg0 0 0 0 -Td]

(2)

其中：Te为发动机激励力矩；Tc为压盘与摩擦片产生的摩擦力矩；Tm为离合器从动盘毂传递力矩；Tg为变速箱内啮合齿轮传递力矩；Td为等效道路力矩。

1.2 离合器黏-滑状态下的摩擦力矩Tc的计算

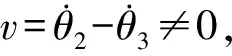
Tf=FμRmzsign(v)

(3)

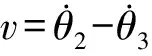
表1 变量及其数值

由于离合器中有波形片的存在，在离合器刚刚开始接合的时候，压紧力从零开始逐渐增大到指定值。假设波形片的轴向刚度为常数，则压紧力计算公式为

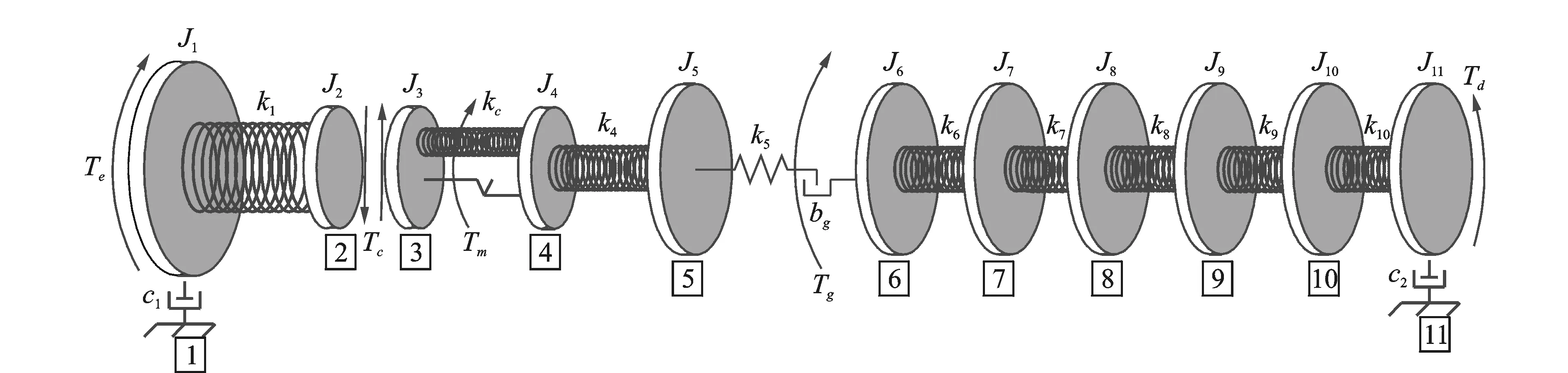
图1 离合器接合过程汽车传动系统动力学模型Fig.1 Dynamic model of automotive driveline

(4)

其中：F0为波形片最大压紧力；te为离合器接合过程中波形片压缩到设定位置所需要的时间。

te的计算公式为

te=F0/κve

(5)

其中：κ为波形片的轴向刚度；ve为波形片在离合器接合过程中轴向压缩速度。

若摩擦片外径为Ro，内径为Ri，当量半径的计算公式为

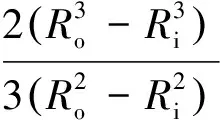
(6)

摩擦因数随相对滑移速度变化的梯度对整个离合器系统的接合过程会产生很大的影响，为了分析该系数对耸车的影响，对摩擦模型进行线性化的假设，将摩擦因数梯度考虑进去，即

μ=μ0+μ′|v|

(7)

其中：μ′为摩擦因数梯度(可以为正、负或0)；μ0为摩擦片静摩擦因数；|v|为主从动盘间的速度差绝对值。

将式(7)代入式(3)中，则滑磨力矩可写成

Tf=Fμ0Rmzsign(v)+Fμ′vRmz

(8)

当离合器处于黏着状态，此时主从动盘之间角速度差v=0，其间的摩擦力矩Tc为静摩擦力矩，根据摩擦的特点，静摩擦力矩和外力相关，有如下函数关系[15]

(9)

其中：Tlock为离合器完全接合后所传递的力矩；Tst为最大静摩擦力矩(Tst=μ0zRmF)。

式(9)中的Tlock为离合器完全接合后所传递的力矩。该力矩可通过对主动盘或从动盘单独进行受力分析获得，其计算公式为

对主动盘分析)

(10)

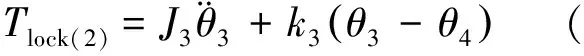
(11)

理论上，通过上述两个公式求得的结果Tlock(1)和Tlock(2)应相等，而在实际的数值计算中，由于误差的存在其值并不相等，为了计算的准确性，可取两结果的平均作为Tlock值

Tlock=(Tlock(1)+Tlock(2))/2

(12)

综上所述，可得到离合器滑动和黏着状态下过程中的摩擦力矩的计算公式

(13)

在计算过程中，由于时间步长和计算误差的限制，即使主从动盘处于黏着状态，其速度差也很难为零，而只是在零速附近，这会使得摩擦力矩不能根据接合状态做出很好的计算。为了保证计算的准确性，可以引入Karnopp摩擦模型[14]。该模型定义了一个零速区间|v|≤D，如图2所示，D为零附近非常小的速度值，根据不同的工作条件而确定。在±D区域外，认为离合器处于滑动状态，摩擦力矩是速度差的函数。而在±D区域内，则强迫认为离合器处于黏着状态，此时摩擦力矩的大小和外力相关。基于以上假定，离合器的摩擦力矩的计算公式为

(14)

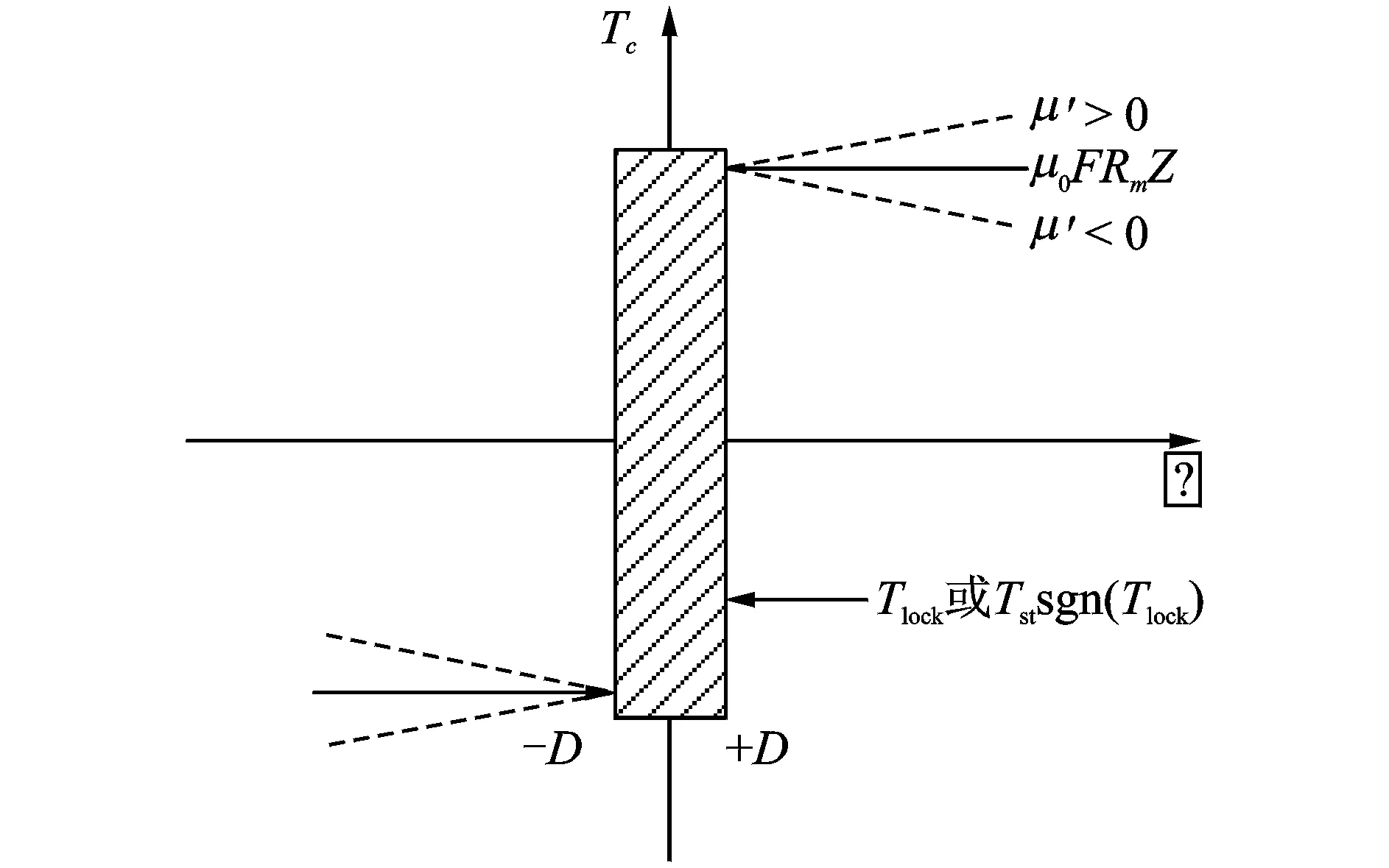
图2 Karnopp摩擦模型Fig.2 Karnopp friction model

1.3 齿轮啮合间隙

变速箱啮合齿轮之间存在间隙，当啮合的轮齿处在间隙范围内，则齿轮传递的扭矩Tg为零。笔者假设齿轮的啮合刚度为定值，利用分段线性的方法建立齿轮传递转矩的数学模型，如图3所示(其中Δ=θ5-θ6)。

根据该模型，变速箱齿轮啮合力矩Tg为

(15)

1.4 离合器从动盘扭转刚度及阻尼

图4所示为典型的离合器静态扭转特性曲线。图4(a)和4(b)表示由于从动盘中的扭转弹簧以及干摩擦阻力产生的力矩，可以看出，离合器从动盘扭转特性较为复杂，扭转刚度和干摩擦阻尼均非线性。图4(c)表明了离合器扭转角δ(δ=θ3-θ4)与所传递转矩Tc的关系。利用分段线性的方法分别对扭转刚度以及干摩擦阻尼进行建模[7-8]。

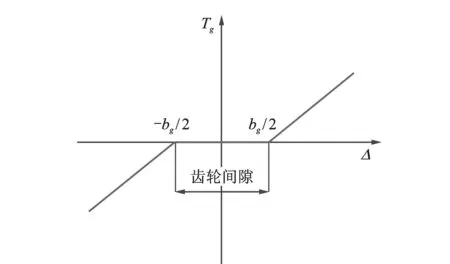
图3 齿轮传递转矩模型Fig.3 Nonlinear gear mesh function

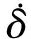
综上所述，离合器通过扭转弹簧和干摩擦阻力所传递的转矩可计算如下

图4 离合器扭转多级非线性特性曲线Fig.4 Profile of a real-life clutch damper

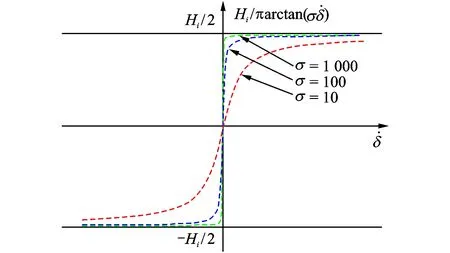
图5 σ对摩擦模型的影响Fig.5 The effect of σ on hysteresis model

(16)

1.5 模型的计算求解

为了对所建立的模型进行数值计算，可将动力学方程(1)写成微分方程的初值问题形式

(17)

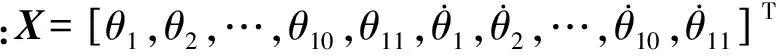
它们分别为

(18)

由于耸车现象主要是由于传动系统自身的振动特性所引起，并且振动频率较低，发动机产生的力矩波动对耸车振动影响不大，因此在所建模型中，将发动机激励简化为一个恒定值。利用表1中的输入参数，可运用4阶龙格库塔方法，对非线性微分方程(17)进行迭代计算。在每一次的迭代过程中，压盘与摩擦片产生摩擦力矩、变速箱内啮合齿轮传递力矩及离合器从动盘毂传递力矩，可分别由式(14)、式(15)和式(16)计算得到。

2 传动系统动态响应计算

2.1 传动系统的固有频率

由于耸车现象是出现在离合器接合完成之后，因此在计算系统固有频率时默认离合器主、从动盘处于接合状态。忽略系统阻尼以及齿轮啮合间隙，计算结果如表2所示。

表2 系统固有频率

Tab.2 Nature frequency of system Hz

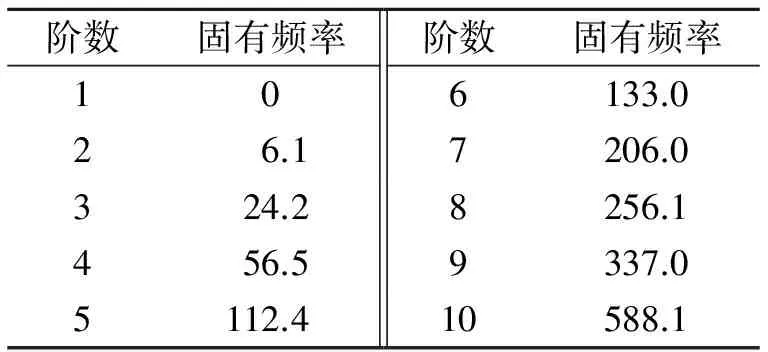
根据表2的计算结果看出，系统第1阶固有频率为零，属于刚体模态。耸车振动的固有频率一般发生在2～8 Hz范围内容，由表2可见，传动系统的第2阶固有频率落在该范围内。图6所示为系统第2阶固频对应的阵型，从图中可以看出，该阶振动形式主要表现为传动系的整体振动，前端振动幅度较大，并且车身振动方向与其余部件相反。

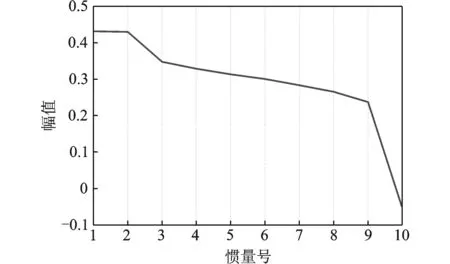
图6 系统第2阶固有频率阵型Fig.6 Mode shape of 2nd order frequency

2.2 系统动态响应的计算结果

利用表1中的参数对第1节建立的动力学方程进行求解，得到从离合器开始接合到汽车完成起步，整个过程发动机和变速器1轴的转速以及车身纵向加速，计算结果如图7所示。由图可见，在离合器刚刚完成接合的时候，发动机与变速箱发生了明显的转速波动，传动系统发生扭转振动。同时，汽车在行驶方向上，车身产生耸车振动。振动频率约为6 Hz，接近于系统的第2阶固有频率，证实了耸车振动是由于汽车起步、离合器接合过程中，传动系统的固有频率与发动机的激励频率接近而产生的振动。由于系统3阶及以上的固频频率较大，振动响应幅值较小，系统振动主要表现为第2阶固有频率的振动响应。

3 试 验

对于汽车起步产生的耸车振动，一般采取主观评价和客观评价两种方法。主观评价是驾驶员和乘员在车辆起步过程中测试人员的感受，客观评价则通过测量离合器接合过程中发动机、变速箱1轴转速和车身纵向加速度振动幅值来进行评定。在测试过程中，将转速传感器置于飞轮和变速箱1轴处，将加速度传感器置于驾驶员座椅导轨上。

先后将2个2级扭转刚度分别为1 000，600 Nm/rad的离合器安装在同一辆汽车上，分别进行测试。测试结果如图8，9所示。由图8 可以看出，离合器接合完成后，发动机转速与变速器1轴出现了非常明显的转速波动。同时，车身也在行驶方向上出现了明显的加速度波动。两次测试，汽车都出现了耸车现象。对比图8和图9可以看出，降低离合器从动盘2级扭转刚度，车身加速度的幅值有了明显的降低，说明降低离合器从动盘扭转刚度可以有效地抑制耸车振动。

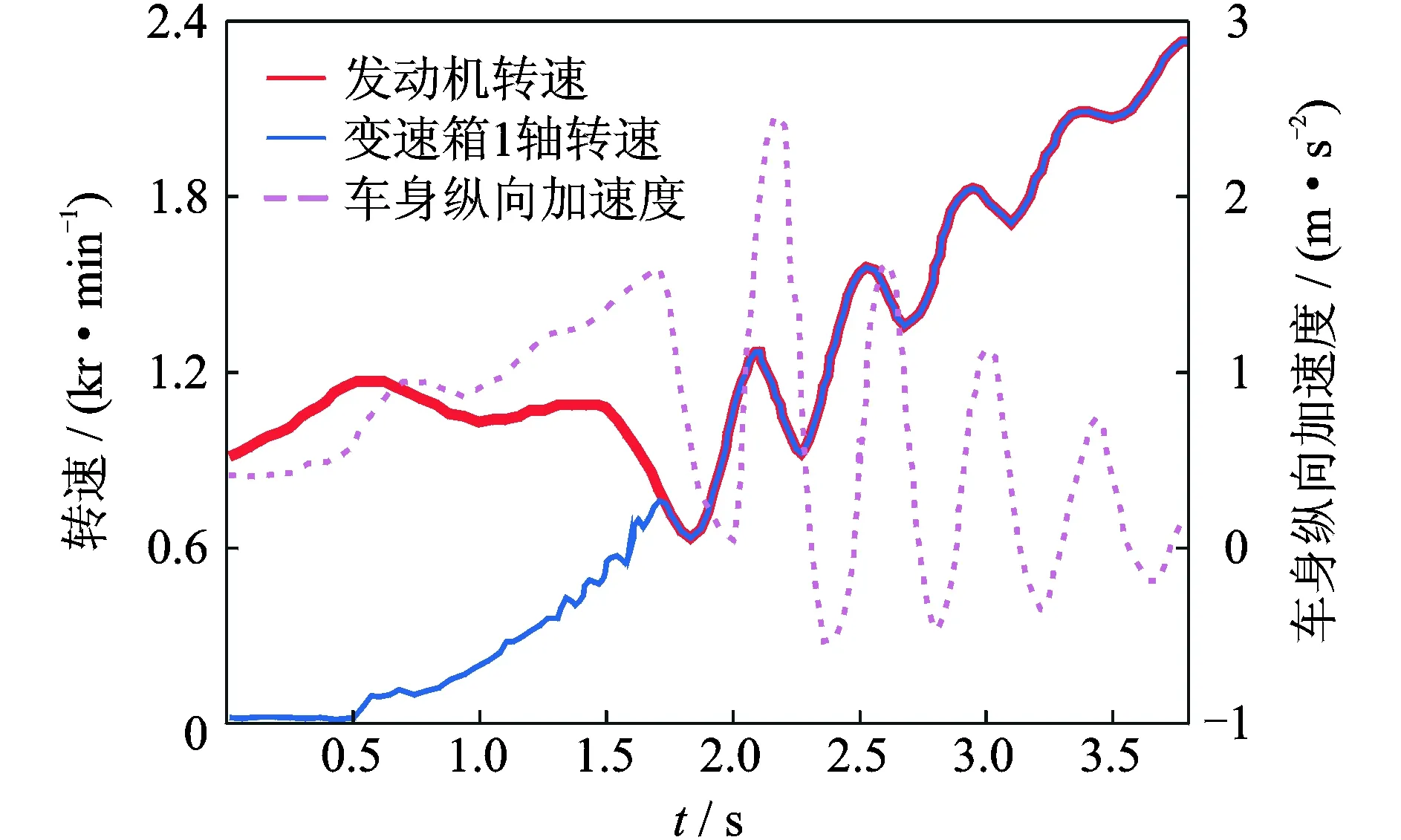
图8 实车测试结果(kc2=1 000 Nm/rad)Fig.8 Result of vehicle experiment (kc2=1 000 Nm/rad)

图9 实车测试结果(kc2=600 Nm/rad)Fig.9 Result of vehicle experiment (kc2=600 Nm/rad)

根据实际测试结果，耸车振动的频率约为2.8 Hz，而计算的耸车振动频率为6 Hz(传动系统的第2阶固有频率)。产生误差的主要原因是在仿真过程中，一些阻尼被忽略，用于计算的部分转动惯量和扭转刚度等参数与实车有一定的区别。此外，在汽车起步的过程中，轮胎与地面存在相对滑动，这同样也会降低耸车振动的频率。但是，利用建立的模型可以模拟与实际测试趋势一致的耸车振动现象，因此，验证了所建立的模型的有效性。

4 从动盘性能对耸车的影响

离合器从动盘是离合器的主要性能部件，它在飞轮和压盘间形成一个摩擦系统，依靠摩擦将动力传递给变速器输入轴。同时，相对于传动系统其他部件，离合器的性能参数比较好调整，因此，笔者将研究的重点放在离合器从动盘性能参数对耸车振动的影响。

4.1 摩擦因数及摩擦因数梯度

离合器主、从动盘之间的静摩擦因数μ是离合器重要的性能参数，直接决定了离合器接合时间，而摩擦因数梯度μ′对汽车传动系的振动有着很大的影响[7]。利用建立的模型，计算在不同静摩擦因数和摩擦因数梯度对离合器接合过程中从动盘振动的影响情况，计算结果如图10，11所示。

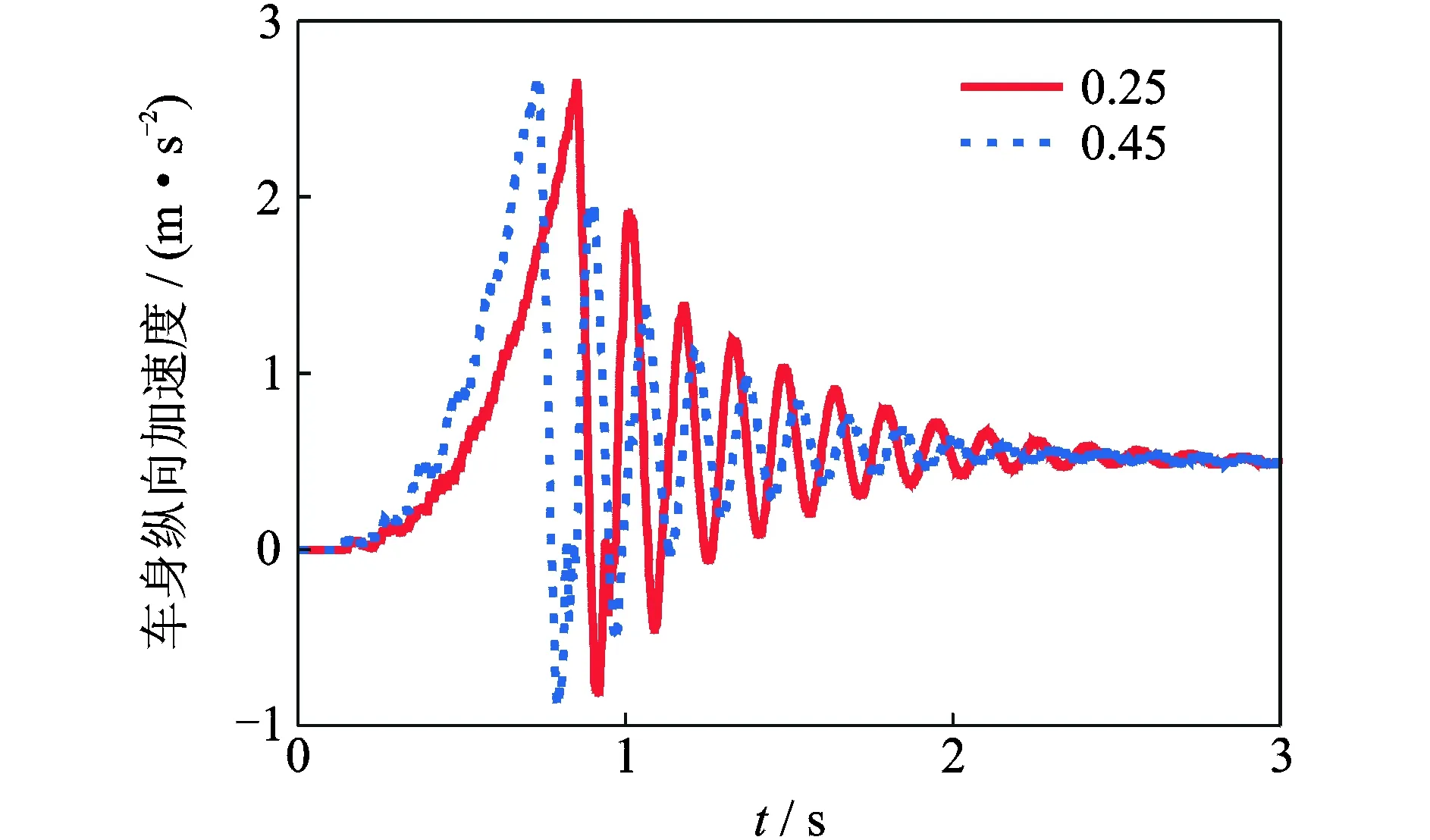
图10 摩擦因数μ对耸车振动的影响Fig.10 Influence of friction coefficient μ on shuffle

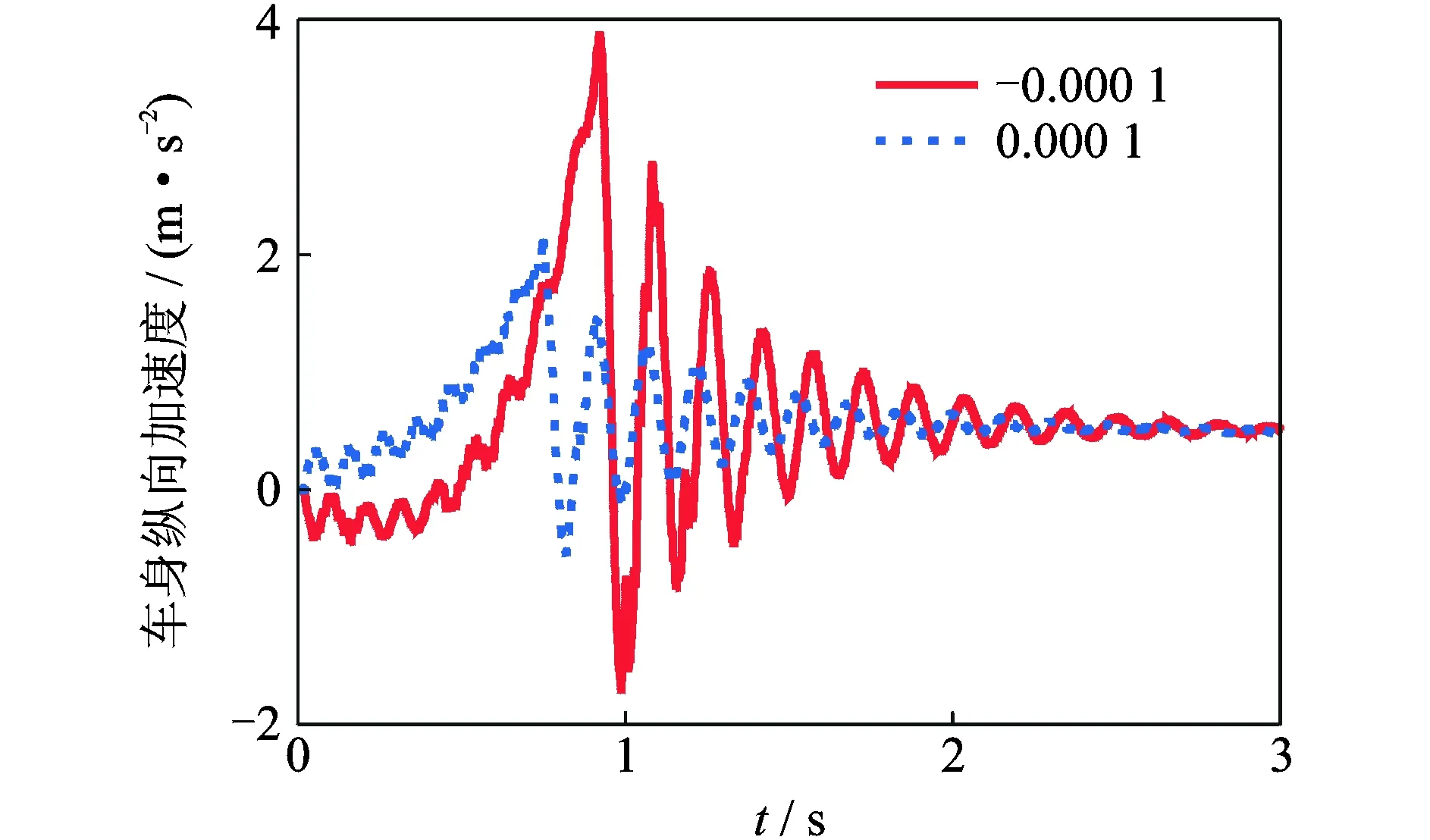
图11 摩擦因数梯度μ′对耸车振动的影响Fig.11 Influence of gradient of the friction coefficient μ′ on shuffle

由图10可以看出，静摩擦因数的增大会使整个离合器接合时间减少，对整个传动系统产生较大的冲击，因此在接合后耸车振动出现的振动峰值较大；但是，相对于较小的静摩擦因数，较大的摩擦因数可以对耸车振动实现更为有效的衰减。因此，适当增加静摩擦因数，不仅可以实现离合器较快的接合，而且可以有效地抑制耸车振动。

由图11可以看出，当传动系统出现摩擦因数负梯度的时候，不仅离合器接合时间会延长，使耸车振动现象更加明显，在离合器接合过程中也会出现非常明显的抖动，加剧传动系的振动。因此，在离合器设计开发的过程中，应适当提高静摩擦因数，并避免摩擦因数负梯度的现象发生。

4.2 从动盘转动惯量和扭转刚度

转动惯量J4和离合器第2级扭转刚度kc2是离合器从动盘重要的性能参数，利用建立的模型计算得到离合器从动盘转动惯量和扭转刚度对耸车振动的影响，计算结果如图12，13所示。

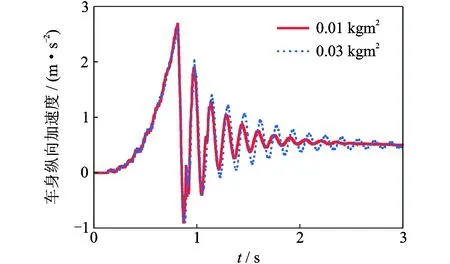
图12 从动盘转动惯量J4对耸车振动的影响Fig.12 Influence of moment inertia J4 on shuffle

图13 从动盘2级扭转刚度kc2对耸车振动的影响Fig.13 Influence of 2nd torsional stiffness kc2 on shuffle

由图12可以看出，从动盘转动惯量的减小，可以在一定程度上抑制耸车振动。但是由于离合器结构紧凑，安装空间较小，因此调整转动惯量的空间不大。

由图13可以看出，当从动盘扭转刚度降低时，可以对耸车振动产生有效的衰减，这一计算结果与上面测试的结果一致。由于离合器从动盘扭转刚度仅由安装在从动盘盘毂上的螺旋弹簧刚度决定，调节方便。因此，适当降低从动盘扭转刚度可以有效地改善耸车振动。但是，从动盘扭转刚度不能太小，这是因为：a.扭转刚度太小，会产生较为严重的起步抖动现象[16]，不利于传动系零部件寿命以及车辆的舒适性；b.扭转刚度的降低，会导致系统固有频率改变，可能会使得系统的某阶固有频率对应的共振转速落在发动机的常用转速之内，传动系会发生共振。

4.3 波形片轴向刚度

离合器波形片对于离合器接合过程中产生的振动主要有两个方面的影响：a.波形片的轴向弹性特性会影响离合器在接合过程中压紧力上升[17]；b.离合器在接合过程中压紧力波动的大小[17]。由于作用在波形片压紧力在离合器设计阶段已经确定，不易改变，因此可以通过改变其轴向刚度来改善起步过程中离合器接合的冲击。

图14所示为波形片轴向刚度κ分别为3 000和4 500 N/mm时，汽车起步车身纵向加速度随时间变化曲线。从图中可以看出，适当降低波形片轴向刚度可以在一定程度上减小汽车起步过程产生的冲击度，但是对耸车振动的衰减并无明显影响。同时，过小的波形片轴向刚度会使汽车起步时间延长，影响汽车动力性。

图14 波形片轴向刚度κ对耸车振动的影响Fig.14 Influence of axial stiffness of waveform cushion κ on shuffle

5 结 论

1) 为了研究汽车耸车振动的问题，建立了整车传动系统11自由度的集总参数模型。模型中，考虑了离合器在接合过程中的黏滑特性、齿轮啮合间隙及离合器从动盘扭转特性等非线性因素，计算分析了传动系统的固有频率和振型。研究表明，耸车振动是由于汽车起步、离合器接合过程中，传动系统的固有频率与发动机的激励频率接近而产生的振动。摩擦因数与相对滑移速度的关系为负梯度时，摩擦过程中会产生自激振动，从而引起耸车。

2) 降低离合器从动盘2级扭转刚度，车身加速度的波动幅值降低，降低离合器从动盘扭转刚度可以有效地抑制耸车振动。

3) 基于建立的动力学模型，分析了离合器从动盘性能参数对耸车振动的影响。分析结果表明，从动盘2级扭转刚度的减小可以有效衰减耸车振动。同时，减小从动盘转动惯量，提高离合器静摩擦因数，也可以在不同程度上改善耸车振动现象，减少汽车传动系统的振动。此外，在离合器设计开发过程中，离合器的摩擦因数梯度为正。

[1] Farshidanfar A, Rahnejat H, Menday M T. Low frequency torsional vibration of vehicular driveline systems in shuffle[C]∥Multi-body Dynamics Monitoring and Simulation Techniques. London: Professional Engineering Publishing, 2000:269-282.

[2] Biermann J W, Hagerodt B. Investigation of the clonk phenomenon in vehicle transmissions-measurement, modeling and simulation[J]. Journal of Multi-body Danamics,1999,213:53-59.

[3] Biermann J W, Reita A, Schumacher T. The clonk phenomenon—a load change reaction to be balanced in terms of comfort and engine response[J]. International Journal of Automotive Technology, 2000, 1(1):56-60.

[4] Menday M T, Rahnejat H, Ebrahimi M. Clonk: an onomatopoeic response in torsional impact of automotive drivelines[J]. Journal of Automobile Engineering,1999,213:349-357.

[5] Vafasi S, Menday M T, Rahnejat H. Transient high-frequency elasto-acoustic response of a vehicular drivetrain to sudden throttle demand[J]. Journal of Multi-body Danamics,2001,215:35-52.

[6] Fanshindiafar A, Ebrahimi M, Rahnejat H. High frequency torsional vibration of vehicular driveline system clonk[J]. International Journal of Vehicle Design,2002,9:127-149.

[7] Centea D, Rahnejat H, Menday M T. The influence of the interface coefficient of friction upon the propensity to judder in automotive clutches[J]. Journal of Automobile Engineering, 1999,219(1):245-258.

[8] 任少云, 孙承顺, 张建武. 某牵引汽车传动系起步扭转振动动态响应分析[J]. 上海交通大学学报,2003, 37(11):1780-1783.

Ren Shaoyun, Sun Chengshun, Zhang Jianwu. Dynamic responses analysis of torsional vibration for a towing tractor driveline system during starting-up phase[J]. Journal of Shanghai Jiaotong University, 2003,37(11):1780-1783. (in Chinese)

[9] 任少云, 孙承顺, 张建武. 考虑齿隙影响的牵引车拖载起步时传动系扭振瞬态响应分析[J]. 振动与冲击,2004,23(3):70-75.

Ren Shaoyun, Sun Chengshun, Zhang Jianwu. Transient torsional vibration analysis during starting of towing tractor for driveline in consideration of gear gaps[J]. Journal of Vibration and Shock, 2004, 23(3):70-75. (in Chinese)

[10] Crowther A, Zhang Nong, Liu Daikai, et al. Analysis and simulation of clutch engagement judder and stick-slip in automotive powertrain systems[J]. Journal of Automobile Engineering,2004,218:1427-1466.

[11] Couderc P H, Callenaere J, Hagopian D, et al. Vehicle driveline dynamic behaviour: experimentation and simulation[J]. Journal of Sound and Vibration,1998,218(1):133-157.

[12] Yoon J Y, Singh R. Effect of the multi-staged clutch damper characteristic on the transmission gear rattle under two engine conditions[J]. Journal of Automobile Engineering, 2013,227(9):1273-1293.

[13] Almahdi S, Michael K, Jason D, et al. Development of refined clutch-damper subsystem dynamic models suitable for time domain studies[J]. SAE Technical Paper Series, 2015,8(2):1-8.

[14] Karnopp D. Computer simulation of stick-slip friction in mechanical dynamic systems[J]. Journal of Dynamic Systems, Measurement and Control,1985,107(1):100-103.

[15] 刘丽兰，刘宏昭，吴子英，等. 机械系统中摩擦模型的研究进展[J]. 力学进展，2008，38(2)：201-213.

Liu Lilan, Liu Hongzhao, Wu Ziying, et al. An overall of friction models in mechanical system[J]. Advances in Mechanics, 2008，38(2)：201-213. (in Chinese)

[16] 胡宏伟，周晓军，杨先勇，等. 离合器起步过程中抖动及其影响因素的分析[J]. 浙江大学学报，2009，43(3)：535-539.

Hu Hongwei, Zhou Xiaojun, Yang Xianyong, et al. Analysis of clutch engagement judder and its influence factors[J]. Journal of Zhejiang University, 2009，43(3)：535-539. (in Chinese)

[17] Rabeih E M A, Crolla D A. Intelligent control of clutch judder and shunt phenomena in vehicle drivelines[J]. International Journal of Vehicle Design, 1996, 17(3): 318-332.

10.16450/j.cnki.issn.1004-6801.2017.06.009

国家自然科学基金资助项目(11472107)；广东省自然科学基金资助项目(2014A030313254，2015A030310383)

2016-03-01；

2016-04-15

U463.211; TH113.1

刘雪莱，男，1988年11月生，博士生。主要研究方向为汽车传动系统振动分析方法与控制。曾发表《离合器压盘热负荷特性分析及改进研究》(《机械传动》2014年第5期)等论文。

E-mail:liuxuelaiaaa@126.com

上官文斌，男，1963年10月生，教授。主要研究方向为汽车振动分析方法与控制、汽车设计理论与方法。

E-mail:sgwb@scut.edu.cn