基于时间序列分析的次均门诊费用及药占比预测分析*

刘 沛 李 阳 郭 威 钟仕洋 熊林平△

·应用研究·

基于时间序列分析的次均门诊费用及药占比预测分析*

刘 沛1李 阳2郭 威3钟仕洋4熊林平2△

目的根据某驻地军队医院门诊费用记录，建立次均费用和药占比的时间序列预测模型，并进行预测分析，为“新医改”政策方案的优化及落实提供决策依据。方法利用SAS9.3统计软件建立ARIMA预测模型，分析2016年的次均费用、药占比的变化趋势。结果①分别采用ARIMA(5,1,0) 和ARIMA(0,1,3)模型对次均门诊费用和药占比进行预测，R2分別为0.946和0.925，且平均相对误差分别为5.23%和3.15%，表明预测效果较好；②次均门诊费用和药占比整体变化不大，分别维持在260元和27%左右；③预测结果显示，药占比月平均增长率为-0.40%，降速较快。结论ARIMA模型是用于医疗费用预测的可靠方法，药占比下降趋势一定程度上反映了政策效果，但应理性看待，综合评判。

时间序列分析 药占比 次均费用 平均增长率 相对误差

“看病难，看病贵”是国家医改过程中亟待解决的民生问题，为缓解百姓“看病贵”问题，国家卫生行政部门将破除“以药补医”机制作为公立医院改革的关键环节[1]，逐步提出取消药品加成政策，建立科学合理的补偿机制。在改革实践过程中，“医疗、医保、医药”三医联动是解决药品加成问题有效途径，全国试点城市也在逐步扩大。药占比即药品费用占患者全部医疗费用比例，是反应药品费用负担情况的一项指标。有统计表明，国内医院收入中药占比平均为40%，而发达国家只有5%～20%，部分发展中国家也只有15%～40%[2]。

江苏省某市是国家第三批公立医疗机构改革试点城市，在国家政策引导下，为实现城市公立医院药品零差率，2015年出台了《城市公立医院医药价格综合改革实施意见》；为杜绝医务人员诸如开大处方、人情方、乱收费等违规行为[3]，2016年建立了按病种付费、按人头付费和按服务项目付费相结合的复合式医保支付方式。本研究拟通过对2005-2015年某驻地军队医院的门、急诊次均费用及药占比变化趋势进行分析，建立时间序列预测模型对其进行预测，为新医改各项政策方案优化及落实提供决策依据。

资料来源与方法

1.资料来源

本文数据包括某三级甲等部队医院2005-2015年的门诊诊疗数据，内容包括：身份类别、费用类别、就诊时间、诊断类型、门诊费用(其中包括：西药费、中成药费、中草药费、检查费等)以及2012-2015年门诊患者的人口统计学特征数据。

2.研究方法

自回归综合移动平均模型(autoregressive integrated moving average model，ARIMA)是Box-Jenkins方法中的重要时间序列模型，它可通过对原时间序列数据差分达到时间稳定化，而残差部分可以通过自回归进行处理，最后综合这些因素建立一个预测模型。然后通过绘制时间序列图判断时间序列数据的稳定性，经过差分和季节性差分转换，使数据可以采用时间序列模型分析[4]。

采用SAS9.3统计软件，利用所获得的某驻地军队医院2005-2015年门诊各项数据，建立ARIMA模型，根据AIC或SBC最小和R2最大选择最优模型，对2016年的次均门诊医疗费用、门诊药占比进行预测分析。

结 果

1.数据说明及序列的平稳性处理

2005-2015年，次均门诊费用月平均增长率为0.28%，且随时间呈现不断上涨趋势(图1)。而药占比月平均增长率为-0.37%，随时间具有明显递减趋势，由于2008年初检查设备的购置，以及医院积极响应国家政策，严格控制药占比，使得2008-2009年药占比急速下降，注意到次均费用在同时期也呈现下降趋势，随后缓慢上升。由于次均费用和药占比均具有非平稳性，通过对次均门诊费用和药占比进行单位根检验，可看出药占比和次均门诊费用一阶差分的序列是平稳序列(P<0.0001)。

2.模型的识别与建立

以次均费用为例，从图2可以看出自相关函数拖尾，偏相关函数截尾。结合典型相关系数平方估计值，初步选择ARIMA(5,1,0)、ARIMA(5,1,1)两个模型做进一步分析。根据模型参数检验结果，按AIC或SBC最小的准则，最终确定ARIMA(5,1,0)为最佳模型，其中AIC=672.78，SBC=687.16。

图1 2005-2015年各月次均门诊费用和药占比波动图

由表1可以看出，ARIMA(5,1,0)模型的几个参数，在α=0.05的显著性水平下，AR(1)、AR(5)均具有统计学意义。由此得到回归模型为：

Xt=-0.61Xt-1-0.14Xt-2+0.02Xt-3-0.08Xt-4-0.34Xt-5+1.03

表1 ARIMA(5,1,0)模型的条件最小二乘估计参数估计结果

3. 模型的检验

模型检验是对模型残差项是否为白噪声过程的检验。如果模型通过检验，则可以进行预测，否则回到建模第二步——对选用模型类型进行重新识别。

图2 一阶差分的自相关函数和偏自相关函数

残差项白噪声检验的原假设为残差项是白噪声，备择假设为非白噪声。从表2中各滞后期的残差项白噪声检验结果可以看出，本序列各滞后期的残差项不存在自相关，即P>0.05，可以认为本研究建立的ARIMA(5,1,0)模型的残差项为白噪声序列。

按照同样的方法，药占比序列经一阶差分处理，得到最优模型ARIMA(0,1,3)，其中AIC=-1041.90，SBC=-1034.0。经残差自相关分析显示，ARIMA(0,1,3)模型的残差项为白噪声序列。

4.模型预测结果分析

图3显示，次均门诊费用和药占比整体变化不大，分别维持在260元和27%左右，次均门诊费用略高于国家2013年卫生和计划生育统计年鉴公布的242.1元[5]，但药占比较统计年鉴数据约低50%。从图3中不难发现，预测值和观测值差异较小，平均相对误差分别为5.23%和3.15%，说明次均门诊费用ARIMA(5,1,0)和药占比ARIMA(0,1,3)模型预测效果较好。

表2 ARIMA(5,1,0)模型残差项的白噪声检验

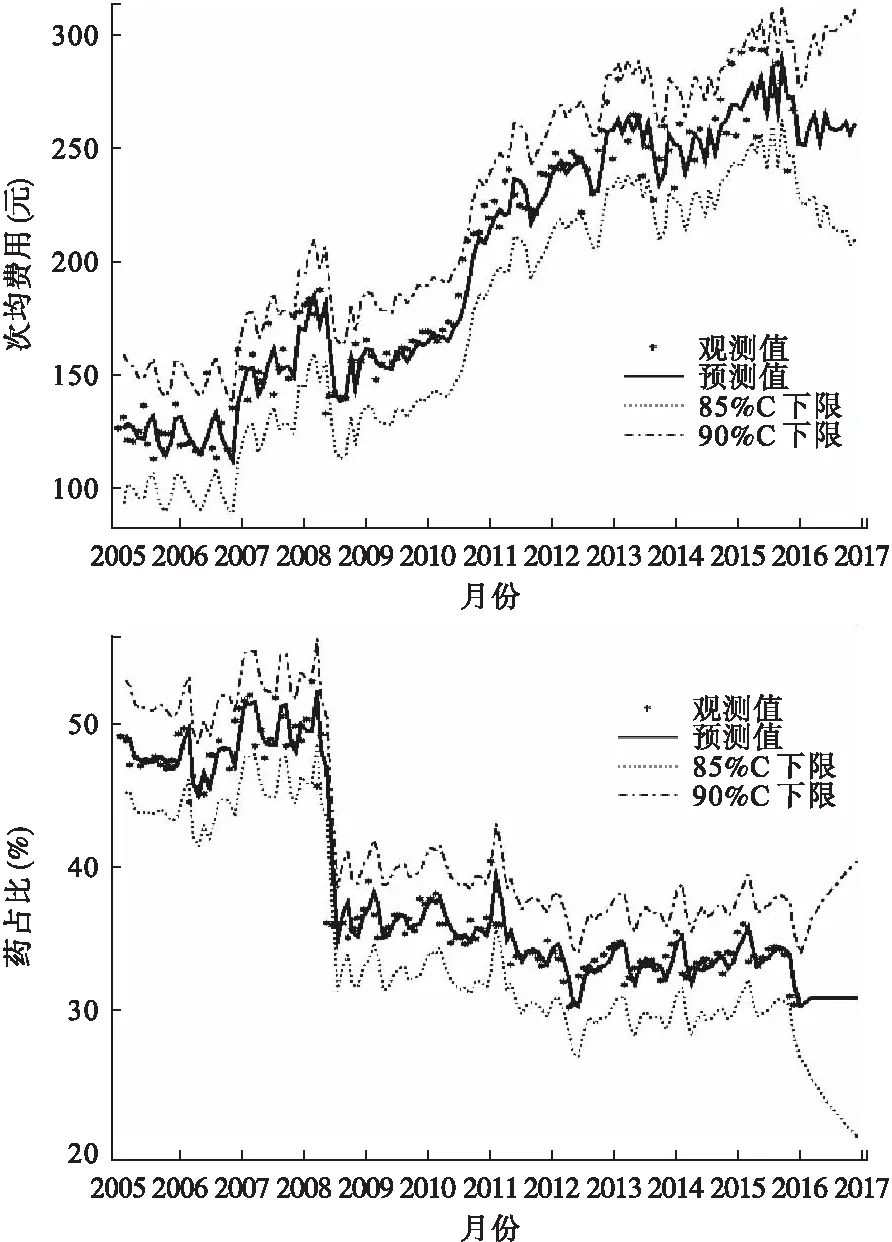
图3 次均门诊费用及药占比的观测值与预测值的时间序列图

2016年次均费用(元)药占比(%)2016年次均费用(元)药占比(%)1月250.229.867月257.329.622月249.930.048月256.229.483月257.530.179月256.929.344月263.230.0310月259.529.205月251.029.9011月254.329.066月263.129.7612月259.028.92

讨 论

1.ARIMA模型的评价与适用性分析

目前国内外应用ARIMA模型预测药占比案例较少，但预测效果较为精准。在本研究中，ARIMA模型能够准确判断次均门诊费用和药占比的动态变化趋势。本研究中分别采用ARIMA(5,1,0) 和ARIMA(0,1,3)模型对次均门诊费用和药占比进行预测，得到平均相对误差分别为5.23%和3.15%，且R2分別为0.946和0.925。这表明ARIMA模型用于医疗费用预测不失为一种较为适用的方法。时间序列分析作为一种分析和预测变量或事物变化趋势的有效统计方法，已经在公共卫生[6-8]、金融[9]、测量[10]等领域得到了较好的应用。

2.合理有效控费是应对医疗费用过快上涨的有效手段

从该院2016年1月-12月次均费用预测结果可知，次均门诊费用月平均增长率为0.13%，门诊医疗费用是持续上涨的。根本原因在于：①医疗资源是有限的，但随着老龄化加剧，疾病谱转变，生活水平提高，百姓医疗服务需求日益增加；②随着经济社会不断发展，人力、物力等成本逐年增加，医院看病成本持续上涨。在医疗费用不断增长的背景下，政府一方面要扩大医疗卫生服务资源，加强成本监管；另一方面要加大财政补贴力度，扩大医保报销范围及比例。

3.药占比部分反映政策效果,应理性看待

从预测结果看，2016年1月-12月，药占比月平均增长率为-0.40%。这表明，随着医药卫生体制改革相关政策的出台落实，药占比随之不断变化，且整体呈现逐年下降趋势，均低于国家2013年卫生统计年鉴数据50.3%。药占比作为破除“以药补医”政策实施效果的重要考核指标，反映了政策实施效果，应理性看待。在医疗费用不断增长的背景下，药占比会受到其他相关费用构成指标影响，单纯看重药占比指标并不能反映药品费用变化的实际情况，会给决策者一种比例降低假象，但实际费用却增加。因此，在补偿机制健全、医务人员合理用药情况下，通过药占比指标进行政策评价才是合理选择。

[1] 中华人民共和国发展和改革委员会.国家发展改革委、卫生部、人力资源社会保障部联合部署县级公立医院医药价格改革工作.2012-09-19,http://www.sdpc.gov.cn/xwfb/t20120919_505777.htm.

[2] 肖平,何光明.控制药品比例医药费用的探讨.中国医院,2009,9(1):34.

[3] 中国社保网.2016年扬州医保支付方式调整方案解读.2016-06-08,http://www.spicezee.com/zhishi/yiliao/134513.html.

[4] 鲍振阳,谭宇,熊光练,等.深圳市医疗费用预测分析及医疗保险基金管理对策研究.中国社会医学杂志,2013,30(5):350-352.

[5] 国家卫生和计划生育委员会.2013年中国卫生和计划生育统计年鉴.中国协和医科大学出版社,2013：107-111.

[6] 高围溦,郭常义,周义军.时间序列分析在我国公共卫生领域的应用.中国社会医学杂志,2011,28(2):78-80.

[7] 梁景星.GM(1,1)灰色模型和ARIMA模型在我院季度入院人数预测中的比较分析.中国卫生统计,2014,31(1):107-109.

[8] 郑骥飞,尹文强,于倩倩,等.基于ARIMA模型的“十三五”期间卫生总费用趋势预测.中国卫生统计,2016,33(5):823-825.

[9] 罗伟伟.时间序列分析在金融中的应用.商,2016,30:173-174.

[10] 孙同贺.时间序列分析在测量领域的应用.测绘与空间地理信息,2013,36(3):12-13.

教育部哲学社会科学研究重大课题攻关项目(16JZD022)；国家自然科学基金项目(71673291) 1.第二军医大学基础部数理教研室(200433) 2.第二军医大学卫生事业管理学教研室 3.第二军医大学卫生统计学教研室 4.武警江苏省总队医院体检科

△通信作者：熊林平，E-mail：xionglinping@aliyun.com

郭海强)