实际复杂约束条件下多星区域覆盖优化算法

章登义 王 争 蔡 波,2*

1(武汉大学计算机学院 湖北 武汉 430072) 2(武汉大学信息中心 湖北 武汉 430072)

实际复杂约束条件下多星区域覆盖优化算法

章登义1王 争1蔡 波1,2*

1(武汉大学计算机学院 湖北 武汉 430072)2(武汉大学信息中心 湖北 武汉 430072)

利用多星协同对大面积区域成像侦测，要求在最短的时间内完成对给定目标区域的完全覆盖，得到卫星每次过境最优侧视观测方案。现有覆盖算法具低效耗时技术瓶颈，有空间覆盖率及时效性局限。充分利用卫星每次过境观测机会，综合考虑相机分辨率、太阳高度角、地面精度等约束条件，依据不同卫星侧摆能力、传感器可视性能以及卫星轨道参数特征，对区域目标进行量化覆盖分析，建立网格划分模型，提出基于一次覆盖策略的覆盖优化算法。该算法能适应实际复杂约束条件，在实际问题规模下，具有良好的效率，能满足工业精度要求。在仿真应用中检验了该算法的有效性和适应性。

成像卫星 区域目标 网格划分 多星覆盖

0 引 言

目前，利用成像卫星侦测地面目标已成为决策部门获取情报信息的重要技术手段。按照与星载传感器视场的相对大小关系，成像卫星的观测目标可分为点目标和区域目标。能够完全被卫星的视场所包含的为点目标，卫星一次扫描无法完全覆盖的为区域目标[1]。点目标相对星载传感器瞬间视场较小，其形状可被忽略并简化以单点经纬度坐标表示。区域目标相对星载传感器瞬间视场较大，通常是由多边形或封闭曲线指出的地面目标，需要多个观测条带才能被完全覆盖[2]。利用多星协同对区域目标成像观测，从而获取更高的时效性和完整性，是卫星成像任务必然需求。当观测目标为区域目标时, 卫星经过目标上空, 选择不同的传感器侧视角可以观测到目标区域的不同部分。为了达到对目标观测的零遗漏，使整个观测过程耗时最短，得到质量更高的图像，每次需要合理选定传感器侧视角度。受卫星飞行轨道、区域范围、相机分辨率以及地球自转等空间因素和过境时间的制约，合理选定一个观测方案实际上是一个基于时空约束的动态组合优化问题。因此，如何合理地设定卫星每次过境侧视角度,以达到对侦查区域较快的完整覆盖，是卫星任务规划领域的重点难题。

本文研究多星协同对区域目标完全覆盖问题，在保证目标区域被完全覆盖的基础上使观测方案时间跨度最短。目前，国内外学者对多星区域覆盖问题研究甚少，对卫星任务规划和调度问题研究较多，而且大都是针对点目标侦察成像[3-6]，不能保证区域观测的完备性，或针对单星的区域覆盖[7-8]，只解决了卫星单次过境区域目标时的观测计划编制问题。对于多星区域目标问题的研究，大多仅谈任务调度，并没有给出具体的覆盖量化分析模型[9-11]。白国庆等[12]采取区域划分方法, 将大面积区域分割为可由单颗卫星一次性完成的子任务。阮启明等[2]采用禁忌搜索算法，应用带最优解记录的禁忌搜索策略减小搜索空间。此两种方法以最大化多星对区域目标总体覆盖率为目标，并不考虑完全覆盖及时效性，不能满足实际复杂条件下多星覆盖任务要求。此外，智能优化算法中的遗传算法和模拟退火算法也是覆盖问题普遍采用的方法[13-14]。这些算法搜索空间大，不确定的因子多，很难确定统一的目标函数。同时收敛性相当依赖初始值的选取，而且都是基于求解一个完整的观测方案得到一个随机解，然后在邻近解空间中迭代寻找更优解的算法。随机解与解空间都基于完整观测方案，而一次观测方案的求解本身是相当复杂且费时的。随着问题规模增大，并考虑实际的精度要求，以上方法的求解在工程实践中并没有多大意义。

本文以成像卫星对目标区域完全覆盖为目标构建问题模型，提出了一种基于一次覆盖策略的求解算法。复杂性不会随着问题规模急剧扩大而显著增加，远远小于遗传算法等智能优化算法，其搜索空间的大小要比穷举法和遗传算法小很多。且该方法只需求解一次完整观测方案，就可以得到一个次优的满意解。同时考虑了覆盖时效性，充分发挥了不同卫星观测能力。

1 问题描述

卫星以推扫方式进行成像，成像卫星以一定空间轨道运行，在地面形成以星下点轨迹为轴线，由侧摆角、视场角和俯仰角等共同确定的成像覆盖条带。多星区域覆盖二维模型如图1所示。多边形区域为目标区域，恰好被三个黑色条带重叠推扫覆盖。

图1 覆盖二维模型图

给定一段足够长时间T，编号为{1,2,…,m}的m颗成像卫星观测某个区域目标Area，这些卫星在时间T内有n次过境，每次过境持续时间tw=[start,end]，称为时间窗口，n次过境活动组成一个窗口集W={tw1,tw2,…,twn}。一个时间窗口twi内，相应卫星以某个侧摆角度θi推扫形成条带覆盖区域Ai。从W中选出p个时间窗口tw1,tw2,…,twp，按开始时间start先后顺序排列，对应卫星条带序列{s1,s2,…,sp}，在这p个时间窗口内条带覆盖区域A1,A2,…,Ap，其相应侧摆角序列Θ={θ1,θ2,…,θp}，获取时间t=endp-start1。

① 太阳高度角约束;

② 成像分辨率约束;

③ 地面网格划分精度约束。

此时Θ={θ1,θ2,…,θp}侧摆角序列是卫星序列{s1,s2,…,sp}的侧摆方案。对于该问题，卫星每次过境以不同侧视角度观测，对应不同的观测条带，取可选的观测带数目为K，取总的观测时间窗口数为N。以计算一个观测方案的时间为尺度，那么时间复杂度为O(KN)，即使K固定不变，该求解也需指数时间。因而，可以认为该问题为NP完备问题，其精确求解是很困难的，只能通过一定的方法求解一个近似的满意解。

2 区域覆盖

本文提出基于一次覆盖策略的搜索算法求解区域覆盖问题，一次覆盖策略是以最大可视覆盖为目标，进行一次完整的全覆盖，找出只被覆盖一次的区域。针对一次覆盖区域，以不同侧视角进行瞬时覆盖搜索，选择覆盖点数最多的侧视角度确定实际覆盖方案。其复杂性不会随问题规模急剧扩大而显著增加，远小于遗传算法，其搜索空间小于穷举法和遗传算法。特别地，当区域离散网格化精度减小，取点数成指数倍增加时，该算法优势更加凸显。

图2为覆盖总体流程图。首先输入仿真参数和约束参数，通过预处理获取卫星过境区域的时间窗口，同时将区域网格离散化。然后通过区域覆盖计算输出最终观测方案。时间窗口是通过STK软件access模块计算得到。区域覆盖计算包括一次覆盖、瞬时覆盖两阶段组成的区域覆盖算法，且该算法依赖条带计算及网格值更新。

图2 覆盖总体流程图

2.1 网格划分

区域覆盖问题的精确求解，需要将区域网格点化，以便在实现轨道仿真的基础上，能够跟踪分析多颗卫星对每一个网格点的重叠覆盖特性，从而进行量化分析。区域目标被网格划分如图3所示。使用等经纬度间隔的网格划分，将单位经纬度矩形区域按边等比划分成多个平面上的网格，用网格中心点代表该网格的整个区域。单位经纬度矩形区域划分比例即为网格精度，不同的划分比例对应不同精度的网格划分，精度越小，单位经纬度区域划分的网格点就越多，目标区域能表示更精细。网格精度取值范围为(0,1〗，一般取0.5、0.25、0.125、0.062 5。如图4所示，单位经纬度区域按不同精度划分。

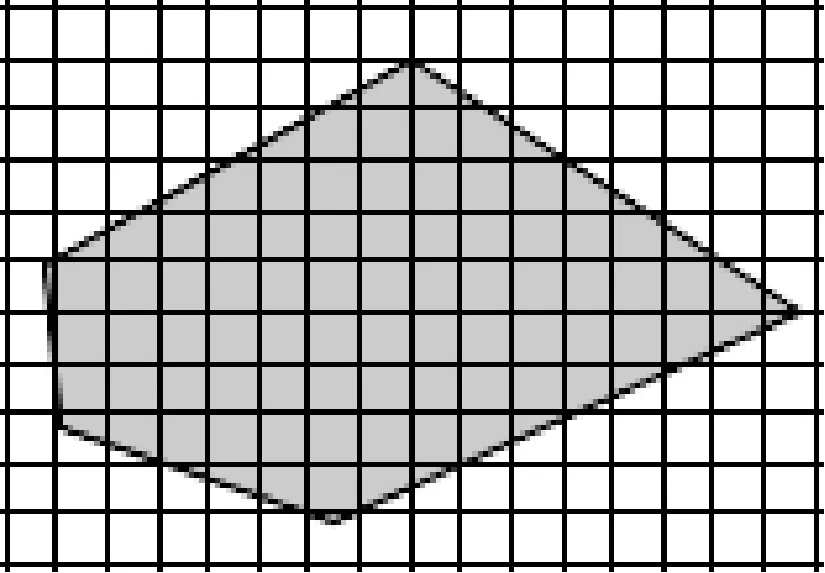
图3 区域划分示意图

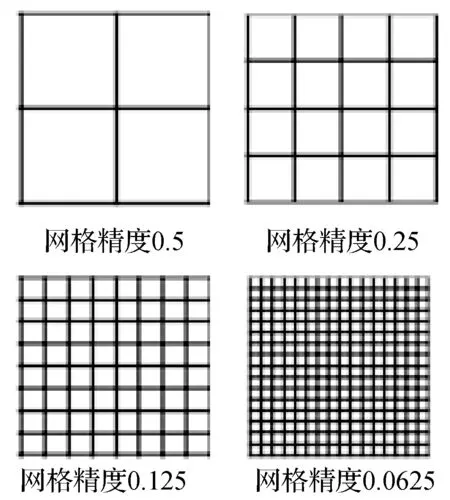
图4 网格精度示意图

定义1网格属性：P=[x,y,t,s]，x、y为网格点的屏幕坐标属性，t为覆盖重数，代表该点被卫星条带覆盖t次，s为条带属性，当t=1，s标记覆盖该点的条带，否则置空。

覆盖条带是由边界多边形定义的区域，覆盖推扫是通过区域填充更新网格属性值，每次推扫以多边形区域内的网格点为集合。

网格精度约束:区域覆盖本质是对网格点进行区域填充，然而此途径并不能判断边界网格是否严格落入覆盖填充区域，因而产生边界误差。取一个更小的网格精度，可以将网格区域划分更加精细，能够减小覆盖求解误差，但覆盖计算处理的网格点增多，增加了覆盖问题求解规模，影响计算效率。实验时网格精度取0.125，在满足计算效率前提下，误差已相对很小。

2.2 多约束覆盖条带计算算法

覆盖条带即卫星在地球上推扫轨迹， 条带由推扫轨迹的边界点序列表示。有如下问题定义：假定相机的垂轨向半视场角为θ(θ定义相机视场边缘与相机中心视轴夹角)，沿轨向半视场角为ϑ，卫星轨道高度为h=r-R，相机沿卫星本体x轴左右侧摆角±β∈[0,βmax]，求相机侧摆情况下在地球上的可视投影及给定时间段内的覆盖条带。可视投影及推扫轨迹如图5所示。

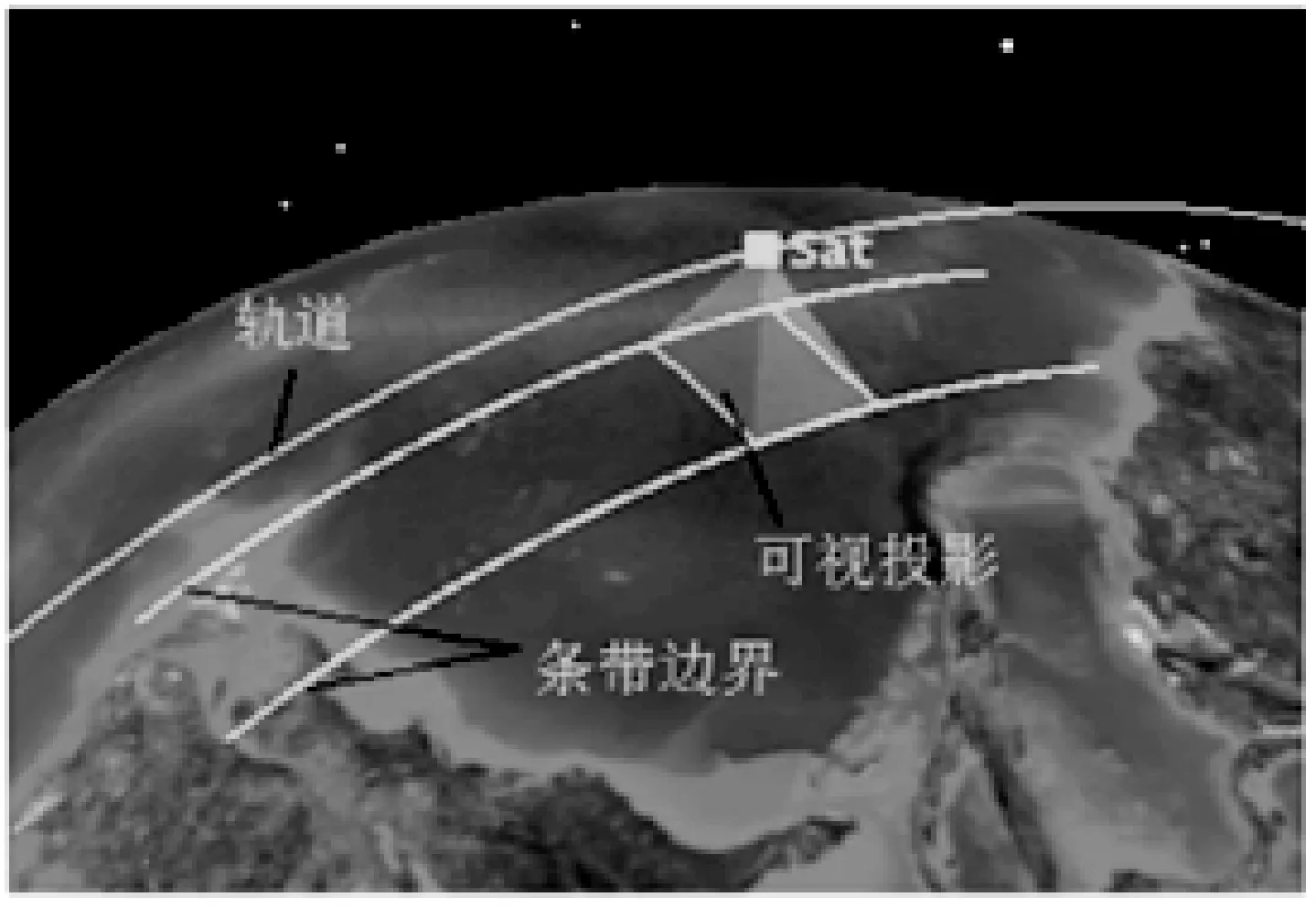
图5 推扫轨迹

卫星t时刻对地可视投影计算的算法步骤如下：

1) 设传感器位置为P，地心为O，根据半角θ、ϑ，以PO为高线，构造代表传感器视场的四棱锥P-Q1Q2Q3Q4。

p′=q×p×q-1

(1)

Si：地心赤道惯性坐标系，So：轨道坐标系，Sb：相机本体坐标系。

从So到Si坐标变换矩阵：

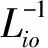
(2)

从Sb到So坐标变换矩阵：

(3)

其中:Ω表示升交点赤经，i表示轨道倾角，u表示纬度幅角(u=ω+τ，ω是近地点幅角，τ是真近点角)，θ是侧摆角，φ是俯仰角，ψ是偏航角。

对任意角γ，

(4)

4) 通过线性插值分别求ΔPQ1Q2、ΔPQ2Q3、ΔPQ3Q4、ΔPQ4Q1与地球椭球面交线。例如求ΔPQ1Q2与地球交线，将线段Q1Q2分n等分，每等分取一点Qi，PQi与椭球面相交得交点，交点序列构成交线。

5) 若以上交线围成闭合区域，则该区域为可视投影，否则以视场边缘与地球表面相切的切线补齐非闭合部分使之闭合，形成可视投影。如图6所示。

图6 可视投影

覆盖条带计算求解步骤如下：

1) 给定起止时间段[t1,t2],步长Δt。

2)t←t1。

3) 重复执行(1)-(3)直到t>t2。

(1) 计算t时刻卫星相机的可视投影;

(2) 以卫星运动方向为参照，取投影上极左极右两点作为条带左右边界点。如图7所示的两种边界凸出情形，利用对称性直接取弧段中点M为极左或极右点。对于图8所示的边界凹陷情形，A、B两点的中点R,地心O与R连线OR，射线OR与球面交点M,取M为极左或极右点;

(3)t←t+Δt。

4) 以上边界点坐标依次转化为经纬度坐标，这些坐标点序列即构成时间段[t1,t2]内卫星覆盖条带。

图7 边界凸出的投影

图8 边界凹陷的投影

相机分辨率约束：

1) CCD传感器相机分辨率计算。CCD传感器像元尺寸D，焦距f，以及侧视角度α，H为轨道高度，计算CCD相机分辨率b，等式如下：

(5)

2) SAR传感器相机分辨率计算。SAR传感器侧视角度φ，C为光速，B为信号带宽，Re为地球平均半径，H为轨道高度，计算SAR相机分辨率b，等式如下：

(6)

3) 分辨率对覆盖的约束。在覆盖分析找一次覆盖状态过程中，卫星以最大视场角对目标区域进行可视覆盖，而最大视场角是由最大侧视角度和最大侧摆时的半视场角决定。最大侧摆时的半视场角固定，根据以上等式，侧视角度越大，分辨率越大。所以不满足分辨率的侧视被忽略。故考虑分辨率的最大视场角度一般比不考虑分辨率的最大视场角度小。体现在一次覆盖状态仿真过程中，覆盖条带变窄。

太阳高度角约束：覆盖过程中，首先要计算卫星对目标可视时间段，来确定可用于覆盖分析的条带。太阳高度角约束了可用于覆盖分析的可视时间窗口，不满足太阳高度角范围的时间窗口被忽略，使可用条带数减少。其约束通过STK接口模块计算实现。

2.3 区域覆盖算法

一次覆盖算法求解该问题虽不具全局最优性，但对规模庞大的NP问题，依然能高效地找到可行解。该算法的搜索起点为最有可能遗漏的点，各卫星以最大视场角计算条带依次对目标区域推扫覆盖，直到完全覆盖。只被覆盖一次的子区域为一次覆盖区域，一次覆盖区域中的点为最有可能遗漏的点，应该被优先覆盖。要求卫星以瞬时视场角、不同的侧视角度对目标区域瞬时推扫覆盖，并根据覆盖策略选取合适的侧视角度加入观测方案。同时从区域目标中去掉选定观测角度推扫过的网格点，形成新的目标区域。然后重复以上过程直至区域网格点数为0。

定义2一次覆盖状态：卫星以最大视场角对区域目标计算可视条带。对于按开始时间排序的条带序列，每个条带依次去覆盖目标区域，直到区域被完全覆盖。这时算法的状态为一次覆盖状态。

覆盖策略1卫星每次以δλ角度为步长更改侧视角度，以瞬时视场角对一次覆盖区域网格进行扫描覆盖。每次推扫覆盖到的网格点属性t加1，未推扫的区域网格属性t不变，每次推扫的侧视角和覆盖面积被记录后，覆盖区域网格属性值重置。最后选择覆盖网格面积最大推扫角度加入侧视方案。

覆盖策略2如果出现多个一次覆盖区域,并且瞬时覆盖后的最大推扫面积相同时，卫星将在目标区域中选择实际覆盖面积最大的侧视覆盖条带确定侧视角。否则，选择最大推扫面积的瞬时覆盖确定侧视角。

策略1网格面积统计仅限于一次覆盖区域，策略2计算实际网格覆盖面积，将统计范围扩大到整个区域目标。每次瞬时覆盖推扫时，既覆盖了一次覆盖区域，又可能覆盖了一次覆盖区域以外的部分目标区域。

算法步骤如下：

拓展时间窗口语义，定义五元组D=[开始时间,结束时间,卫星代号,侧视角度,一次覆盖标识]，一次覆盖标识为-2、-1、0、1，分别表示时间窗口被分配、不可用、待分配、对应条带为一次覆盖条带，初始为0。

1) 预估并设定仿真时间段T，保证这些卫星在该时间内足够完成对目标区域的覆盖。

2) 设定网格精度划分网格，输入分辨率阈值、太阳高度角上下限、侧视步长δλ。

3) 根据时间段T和太阳高度角约束，获取所有卫星对目标区域可视时间窗口，生成时间窗口五元组序列DS，这些元组按开始时间先后顺序排序。

4) 区域M初始为区域目标所包含的网格集，网格属性t初始为0。

5) 重复执行步骤(1)-步骤(5)，直至M=∅。

(1) 重复执行步骤①-步骤③，直至找到一次覆盖状态或DS被遍历完毕;

① 每次从序列DS中按顺序取出一个元组d,如果元组d覆盖标识为-2或-1，则跳到①，否则执行下一步;

② 元组d覆盖标识置0，对d所属卫星进行分辨率约束检验，并计算满足约束的最大视场角，若无法满足约束，则置其覆盖标识为-1;

③d所属卫星以最大视场角计算条带，对区域M进行重叠覆盖。

(2) 如果没找到一次覆盖状态，则跳到步骤2)，重新预估T或调整约束条件。

(3) 扫描区域M内所有网格点，如果网格属性t=1，则根据网格条带属性s置对应时间窗口五元组的覆盖标识为1。

(4) 遍历DS，对一次覆盖标识为1的时间窗口五元组d，所属卫星在相同时间段以确定的瞬时视场角度，δλ为步长，选择不同的侧视角度计算覆盖条带依次对区域M进行推扫覆盖，根据以上覆盖策略确定最终的侧视角θ，更新元组d侧视角度为θ，置其覆盖标识为-2，记侧视角θ时的推扫区域网格集为m。

(5) 令M=M-m，网格点属性值重置。

6) 根据DS输出侧视序列方案。

图9演示了求一次覆盖区域过程。图9(a)表示目标区域，图9(b)-图9(e)表示条带S1、S2、S3、S4依次对目标区域进行覆盖推扫，寻找一次覆盖状态。第五步找到一次覆盖状态，目标被完全覆盖。第六步表示通过推扫覆盖得到两个阴影区域A1、A2，代表一次覆盖区域。A1只能被条带S2单独一次推扫，A2只能被条带S4单独一次推扫。

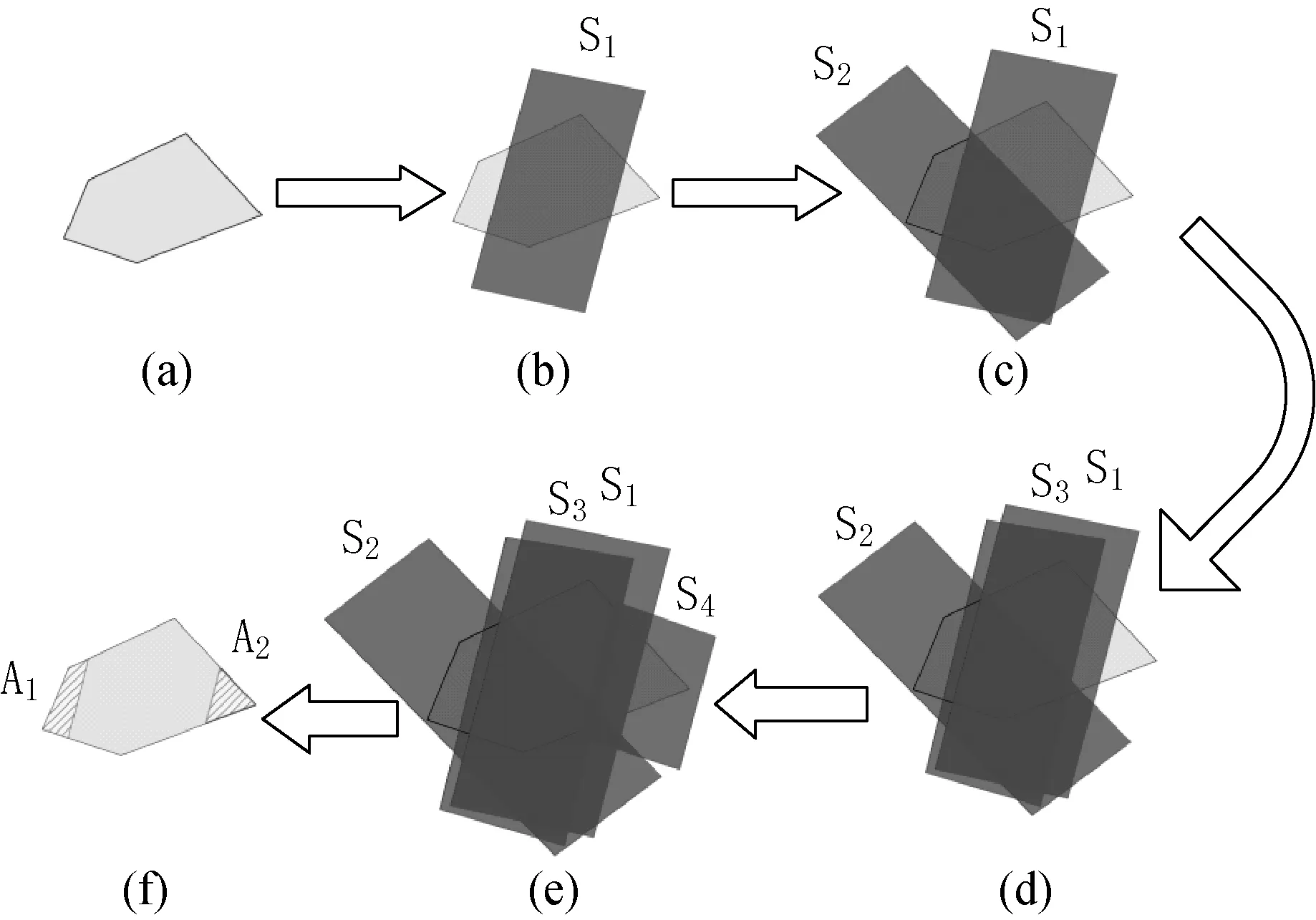
图9 一次覆盖过程

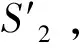
图10 瞬时覆盖过程

图11 新的目标区域

3 实验结果及分析

为检验本文模型及算法，以运行时间、覆盖获取时间、覆盖重数为指标，进行如下仿真实验。

仿真时间：2015/12/21 12:00:00-2016/01/05 12:00:00。

网格精度：0.125。

推扫步长δλ：1°。

轨道参数：用到四颗光学卫星1-卫星4，轨道历元时间为2015/7/1 12:00:00。表1为初始轨道根数。

表1 卫星轨道参数

目标区域：Area1-Area3，顶点经纬度定义如表2所示。

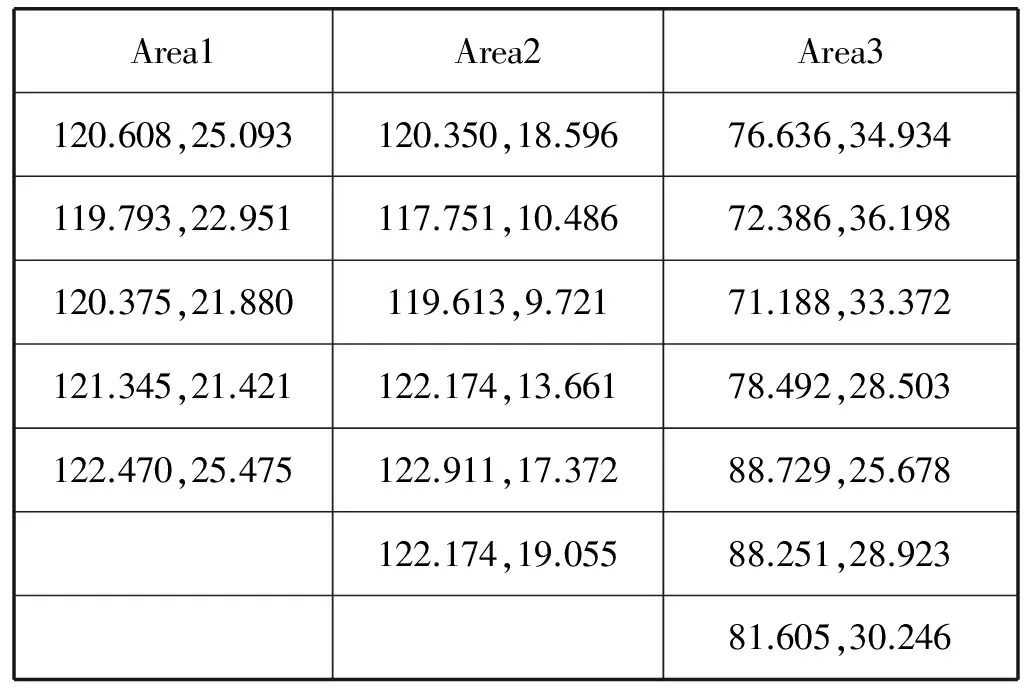
表2 区域目标定义

成像条件：分辨率阈值取10 m，太阳高度角范围 (0°,90°)，传感器垂轨向半视场角5°，沿轨向半视场角1°，最大侧摆角40°。

根据以上仿真数据，应用本文算法做了5组实验，得表3所示结果。在0.125网格精度下，区域Area1、Area2、Area3网格点数分别为414、1 687、3 971。实例一、二、三用于验证区域大小对覆盖的影响，相同卫星对不同区域覆盖，区域大小对覆盖获取时间影响显著，对计算效率影响不明显。说明该算法复杂性没有随着问题规模急剧扩大而显著增加，具有良好适应性。实例三、四、五区域目标均为Area3，卫星资源增加，运行时间没有显著变化，获取时间显著减小，具有更好的时效性，卫星协同观测能力得到充分发挥。统计以上5个实例区域的覆盖结果，得到图12所示重数统计图。一重保持较高占比，一重与二重比率能达到80%～90%，且相对卫星数目，实例的重数也不高，说明该算法覆盖冗余比较理想，覆盖效果良好，通过该算法可高效获取满意解。

表3 仿真结果

图12 重数统计图

禁忌搜索算法、遗传算法、本文算法性能比较如表4所示。其中区域大小表示算法适宜处理的最大区域，用区域网格点数量级衡量。从表4中可以看出：本文算法在实际约束、覆盖时效性、运算效率、区域大小等性能方面占较高优势，具良好的适应性。表5是以上算法计算效能的对比。由于禁忌算法及遗传算法是比较复杂的智能算法，在规模较小的实例下，容易找到最优解，本文实例一、实例二规模较小，禁忌算法及遗传算法求得的解优于本文算法，但本文算法运算效率较高。随着问题规模的增大，本文算法运算效率、覆盖时效性方面的优势更加凸显。

表4 算法性能对比

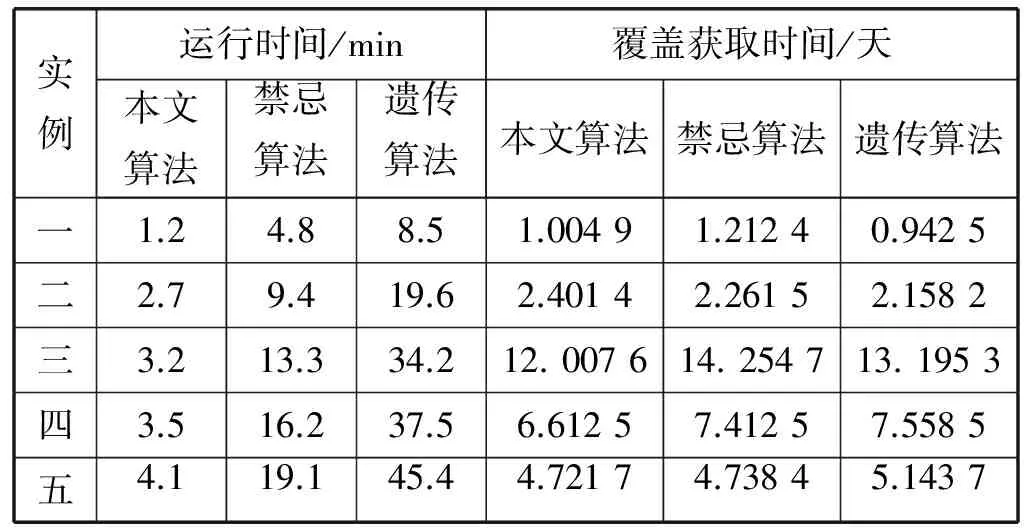
表5 算法计算效能对比

4 结 语

本文对多星多约束区域目标覆盖问题进行了研究，构造了网格划分量化分析模型。通过几何方法计算卫星覆盖条带，在此基础上提出了基于一次覆盖策略的求解算法。仿真结果表明：该模型及算法能够有效求解出一个满意解，且相比以往算法，该算法可以有效处理规模较大的问题。随着卫星数增加，完成覆盖所需获取时间显著减小，充分发挥不同卫星的观测能力且能够满足一定的时效性。然而，考虑到覆盖卫星增多，条带花费有增加的趋势，且仍存在诸多可编排的卫星条带，资源还有很大节省空间。下一步可以尝试覆盖结果的二次优化，充分发挥卫星观测能力的同时，尽可能节约卫星资源。

[1] 白保存,阮启明，陈英武.多星协同观测条件下区域目标的动态划分方法[J]. 运筹与管理, 2008, 17(2):43-47.

[2] 阮启明,谭跃进,李永太,等. 基于约束满足的多星对区域目标观测活动协同[J]. 宇航学报, 2007,28(1):238-242.

[3] Globus A, Crawford J, Lohn J, et al. A comparison of techniques for scheduling earth observing satellites[C]//Nineteenth National Conference on Artificial Intelligence, Sixteenth Conference on Innovative Applications of Artificial Intelligence, July 25-29, 2004, San Jose, California, Usa. DBLP, 2004:836-843.

[4] Tinker P, Fox J, Green C, et al. Analogical and case-based reasoning for predicting satellite task schedulability[C]//International Conference on Case-Based Reasoning. Springer Berlin Heidelberg, 2005:566-578.

[5] 李菊芳,谭跃进.卫星观测系统整体调度的收发问题模型及求解[J].系统工程理论与实践, 2004, 24(12):65-71.

[6] Chen H, Li J, Jing N, et al. Hybrid Algorithms for Electromagnetic Detection Satellites Scheduling[C]//20th IEEE International Conference on Tools with Artificial Intelligence, 2008:411-418.

[7] Lin W C, Liao D Y, Liu C Y, et al. Daily Imaging Scheduling of an Earth Observation Satellite[J].IEEE Transactions on System, Man, Cybernetics,2005,35(2):213-223.

[8] 章登义，郭雷，王骞，等. 一种面向区域目标的敏捷成像卫星单轨调度方法[J]. 武汉大学学报·信息科学版，2014,39(8):901-905.

[9] 李曦,祝江汉,毛赤龙.多卫星区域观测任务的效率优化研究[J].计算机仿真, 2006, 23(12):24-27.

[10] 王慧林,黄维,马满好.面向区域的电子侦察卫星规划系统设计与实现[J].计算机工程与应用, 2010, 46(27):209-213.

[11] 贺川, 朱晓敏, 邱涤珊. 面向应急成像观测任务的多星协同调度方法[J]. 系统工程与电子技术, 2012, 34(4):726-731.

[12] 白国庆,白保存,徐一帆.多星协同对区域目标观测的动态划分方法[J]. 测绘科学, 2010, 35(6): 32-35.

[13] 白保存.考虑任务合成的成像卫星调度模型与优化算法研究[D].长沙:国防科技大学,2008.

[14] 王迪,祝江汉,薛波.基于GA的电子侦察卫星任务规划问题研究[J].计算机仿真, 2009, 26(8):53-56.

MULTI-SATELLITEREGIONCOVERAGEOPTIMIZATIONALGORITHMUNDERREALCOMPLEXCONSTRAINTS

Zhang Dengyi1Wang Zheng1Cai Bo1,2*

1(SchoolofComputer,WuhanUniversity,Wuhan430072,Hubei,China)2(InformationCenter,WuhanUniversity,Wuhan430072,Hubei,China)

Using multi-satellite co-operation to detect large area, it is required to complete the full coverage of a given target area in the shortest time, and obtain the optimal side-view observation scheme for each transit. The Existing coverage algorithm has the disadvantages of time-consuming and low efficiency technology bottleneck, spatial coverage rate and time limitations. In this paper, we took full advantage of the opportunity of each transit observation of the satellite, considering the constraints such as camera resolution, solar elevation angle and ground precision. Based on the characteristics of satellite side swing, sensor visual performance and satellite orbit parameters, the regional target was covered by quantitative coverage analysis, and the grid partitioning model was established. A coverage optimization algorithm based on one coverage strategy was proposed, which could adapt to the practical complex constraints conditions, in the actual problem scale, with good efficiency, to meet the industrial accuracy requirements. Finally, the effectiveness and adaptability of the algorithm were verified in the simulation application.

Imaging satellite Regional target Grid partition Multi-satellite coverage

2016-11-18。国家科技支撑计划项目(2012BAH35B02)；国家自然科学基金项目(41301409)。章登义，教授，主研领域：空天信息仿真及卫星调度。王争，硕士生。蔡波，副教授。

TP3

A

10.3969/j.issn.1000-386x.2017.12.001