阶梯形丁坝下游回流规律分析

钟 亮， 孙建云， 刘珺洁， 周鑫靖

(1. 重庆交通大学 国家内河航道整治工程技术研究中心， 重庆 400074； 2. 重庆交通大学 水利水运工程教育部重点实验室， 重庆 400074； 3. 重庆市信息通信咨询设计院有限公司， 重庆 400041)

阶梯形丁坝下游回流规律分析

钟 亮1, 2， 孙建云2， 刘珺洁2， 周鑫靖3

(1. 重庆交通大学 国家内河航道整治工程技术研究中心， 重庆 400074； 2. 重庆交通大学 水利水运工程教育部重点实验室， 重庆 400074； 3. 重庆市信息通信咨询设计院有限公司， 重庆 400041)

阶梯形丁坝在航道整治中应用广泛，其回流规律与船舶通航、坝田淤积及堤岸稳定等系列问题密切相关，但目前研究很少。应用三维水流数学模型研究双级阶梯形丁坝几何尺度及来流条件对回流规律的影响，结果表明：①回流长度随一级丁坝相对长度ε1及高度ψ1、二级丁坝相对长度ε2均呈递增变化趋势，随弗劳德数Fr呈先增大后减小的变化趋势；②回流宽度随ε1，ε2和ψ1变化相对明显，而随Fr变化总体较小；③回流正、负流区宽度比沿程变化曲线总体为上凸状，负流区宽度相对较大，在靠近丁坝部位可达正流区宽度的2.5倍；④回流曲线形态与ε1，ε2和ψ1有关，ε1和ψ1主要影响回流曲线长度，ε2影响回流曲线的整体形态；⑤回流流量一般小于来流量的10%，沿程分布曲线不对称，增流区回流流量变化相对缓慢，而减流区变化相对剧烈。

阶梯形丁坝； 回流尺度； 回流曲线； 回流流量

丁坝是常见的航道整治建筑物，具有改善航道、维护河相和保护水生态等功用。航道整治中，一般可根据滩险碍航特性选用某级水位将丁坝设计成单一断面型式(以下简称“单式断面丁坝”)，但在某些河段，由于汛期淤积严重，退水期冲刷不及，经常出浅碍航，如果只采用一级整治水位将难以达到设计的航道尺度标准。为使洪水期少淤，退水期早冲，必须采用中水整治(或洪水整治)与枯水整治相结合的方法，同时为减小对洪水壅高的影响，较高一级整治水位所对应的整治线宽度必须适当增加[1]，从而形成阶梯形丁坝(或称“复式断面丁坝”)。目前，阶梯形丁坝已广泛应用于诸多河段的航道整治工程中，如三峡水库变动回水区胡家滩滩段、珠江三角洲的东平水道、顺德菊花湾险段以及西江中游界首至肇庆河段等[2]。

丁坝的修建将改变河床局部形貌并形成独特的水流流态，回流区是丁坝水流分区的重要组成部分，其水力特性直接影响船舶通航、坝田淤积及堤岸稳定，一直备受学术界和工程界关注。比如回流尺度方面，冯永忠[3]探讨了错口丁坝的回流长度、回流与主流分界线及其最大宽度问题；李国斌等[4]研究了非淹没丁坝下游回流长度及最大回流宽度的影响因素；韩玉芳等[5]分析了丁坝回流长度与丁坝附近河床冲刷发展过程的变化关系； Ettema等[6-7]讨论了丁坝回流边线及分离区尺度问题；陈稚聪等[8]探讨了丁坝回流横向和纵向分区问题，分析了回流尺度及流量沿纵向的变化规律；郑艳等[9]研究了丁坝长度对回流长度的影响规律；马永军等[10-11]讨论了减小丁坝下游回流尺度的有效方法。然而，上述研究都是针对单式断面丁坝的，工程实践表明，当河道水位介于两级整治水位之间形成非淹没阶梯形丁坝时，下游回流规律将受两级丁坝几何尺度和水流条件的影响，较单式断面丁坝更为复杂，但目前相关研究还鲜有涉及。为此，本文将以非淹没阶梯形丁坝为例，探讨双级丁坝几何尺度和来流条件对回流规律的影响，研究结果可为工程设计提供参考。

1 数学模型及其验证

1.1 模型建立

1.1.1基本方程 本文应用三维浅水运动数值模拟开展研究，垂向采用分层二维计算方法，基本控制方程为：

连续方程； ∂u/∂x+∂v/∂y+∂w/∂z=0

(1)

动量方程：

(2)

式中：x，y，z为笛卡尔坐标的3个方向；u，v，w分别为x，y，z向的流速分量；t为时间；ρ为水的密度；P为水压力；f为柯氏系数，f= 2Ωsinφ，Ω为地球自转角速度，φ为当地地理纬度；τxx，τxy，τxz，τyy，τyx，τyz分别为剪切应力张量的分量；Ax，Ay分别为x，y向的紊动扩散系数；Δ为拉普拉斯算子；P0为水表面处大气压力；g为重力加速度；H为水深。

根据线性k-ε紊流模型，剪切应力张量的分量τij可表示为：

(5)

式中：νt为紊动黏滞系数；δij为Kronecker delta符号，当i=j时，δij=1，否则δij=0；k为紊动能，ε为紊动能耗散率，求解方程为：

模型中参数取值为：Cμ=0.09，C1=1.44，C2=1.92，σk=1.0，σε=1.3。

1.1.2数值方法 基本控制方程组采用有限体积法离散求解，平面为非结构化的三角形网格，垂向选用分层结构化网格。压力和速度场耦合计算采用SIMPLEC算法，代数方程组采用交替方向隐式迭代算法(ADI算法)和三对角矩阵算法(TDMA算法)求解，计算收敛准则为所有变量的最大无量纲残差小于10-5。

1.1.3边界条件 设定水槽左、右两岸均为陆边界，水流的法向分量恒为0；进口边界给定初始流速、紊动能及其耗散率；出口边界给定法向零梯度假定；固壁边界考虑壁面影响，将壁面应力加入方程并修正相应的边界系数和源项；采用VOF 法计算自由水面。

1.1.4计算参数 计算中最大、最小时间步长分别取0.2和0.001 s；临界柯朗数取0.8；为避免水深为0或较小时出现计算机数值溢出或发散，设置了干湿单元临界值，干水深hd= 0.005 m，湿水深hw= 0.10 m，容许淹没水深hf= 0.05 m。

1.2 模型验证

1.2.1水槽试验 采用水槽试验资料进行模型验证，试验在重庆交通大学国家内河航道整治工程技术研究中心进行，整个循环装置包括水池、泵站、平水塔、量水堰、进水前池、矩形直道水槽、尾水闸门和循环水廊道，水槽长48 m、宽2 m、高1 m，其侧面与底面均采用混凝土抹面，底坡为5‰。丁坝布设在水槽左岸，丁坝轴线距水槽进口断面28 m，确保来流平顺并接近均匀流，距水槽出口20 m，使回流得以充分发展和衰减。丁坝采用双级阶梯形断面，一级丁坝长b1=80 cm、高D1=15 cm，二级丁坝长b2=40 cm、高D2=35 cm，不考虑丁坝顶部宽度和上、下游边坡的影响，设计成顶宽10 cm的直立式丁坝，坝头为半圆形，各级丁坝均采用混凝土制作，并在表面涂上一层红漆(见图1)。

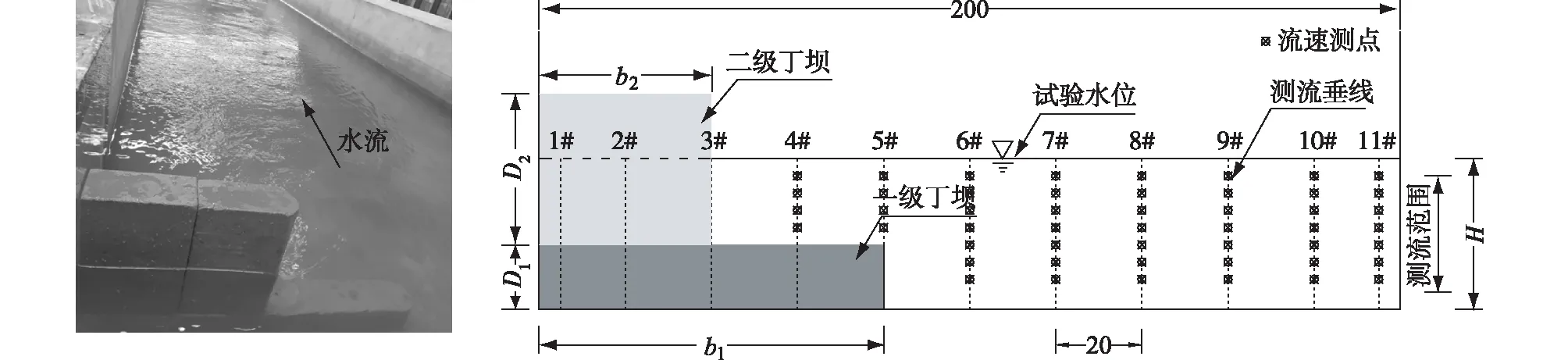
图1 阶梯形丁坝及流速测点布置(单位： cm)Fig.1 Arrangement of step-shaped spur dike and velocity measuring points (unit: cm)

试验流量Q=190 L/s，尾门断面水深H0=0.35 m。流量采用量水堰控制。水位采用SCM60型测针观测，沿程布置了17个观测断面。流速采用Vectrino小威龙流速仪观测，共布置7个观测断面(CS1～CS7)，丁坝轴线位于CS3，上游CS1～CS2断面距丁坝轴线分别为75和25 cm，下游CS4～CS7断面距丁坝轴线分别为25, 50, 100和150 cm。各断面沿宽度方向均布设11条测流垂线，垂线间距20 cm(近壁垂线距边壁约5 cm)；流速采集的水深范围为4～31 cm，流速测点间距4.5 cm，其中一级丁坝顶部各垂线布置4个测点，其余各垂线布置7个测点，采样点位于流速仪正下方4 cm处。

数模计算沿水深方向等分为9层，平面采用三角形网格，全计算域共252 045个单元、14 475个节点，丁坝区域计算网格边长2 cm，其余区域网格边长逐渐过渡至8 cm。

1.2.2水位验证 选择水槽左侧、中轴和右侧3条纵向水面线进行验证，验证结果见图2，图中横坐标为采用沿程距离x与一级丁坝长度b1之比的相对沿程距离，纵坐标为采用当地水位z与尾门断面水位z0之比的相对水位。结果显示，丁坝所在的左侧上游自由水面逐渐升高，至坝前达到最大值，坝后水面线快速下降，此后缓慢上升，至x/b1=15处基本保持稳定；中轴和右侧水面线变化基本一致，丁坝断面(x/b1=0)上游水位缓慢下降，至丁坝前缘受束流影响水位急剧下降，过丁坝后水流扩散，水面逐渐上升，直至保持稳定。从验证效果看，计算和实测水面线总体吻合，水位非常接近。

图2 水位验证Fig.2 Verification of water level

1.2.3流场验证

(1)平面流速分布 根据水槽试验测流情况，图3给出了距槽底0.78H层和0.43H层(H为丁坝断面平均水深)的流场分布对比，可见，计算和实测流场的流速分布形态及大小较接近，均揭示了坝头分离流和坝后回流。

图3 平面流场验证Fig.3 Verification of plane flow field

(2)垂线流速分布 限于篇幅，图4仅给出了丁坝断面(CS3)上4条代表垂线的纵向流速垂线分布验证情况，图中y/B(水槽宽度B=2 m)为距左侧边壁的相对距离，u/U0为采用尾门断面平均流速无量纲化后的流速。验证结果显示，计算与实测流速大小及垂线分布均较为吻合。

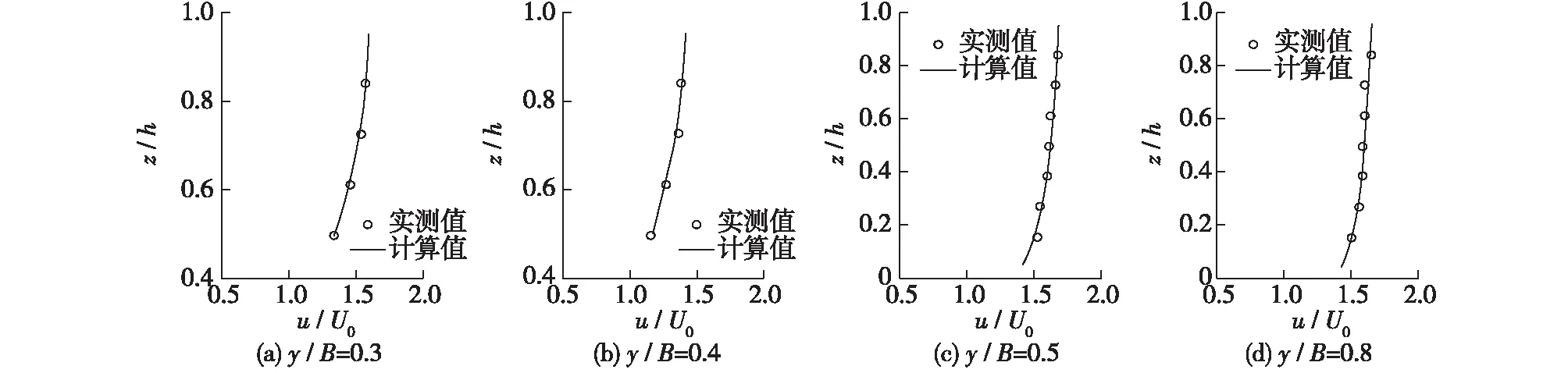
图4 纵向流速垂线分布验证Fig.4 Vertical distribution verification of longitudinal velocity

综上水位和流场验证结果，表明本文数学模型合理，结果可靠，可用于下一步研究。

2 结果与讨论

2.1 丁坝回流区界定

研究[8]表明，丁坝回流区可进一步划分为正流区和负流区(见图5)，划分方法如下：回流发生并稳定后存在一条曲线AB，此线内侧区域为回流区，外侧区域为主流区，主流区流量始终等于上游来流量；回流区内的纵向流速有正有负，正、负向流速交界曲线AC的纵向流速为0，以曲线AC为界，内侧区域称为负流区，外侧区域称为正流区，正、负流区的纵向流量绝对值相等而方向相反，处于自成体系的动平衡状态。在回流区，前段(DO区段)为回流增流区，回流流量沿程逐渐增加，后段(OE区段)为回流减流区，回流流量沿程逐渐减小，增流区和减流区的分界点O处回流流量最大。

图5 丁坝回流区划分示意Fig.5 Partition of backflow region

2.2 回流参数变化分析

定义一级丁坝相对长度ε1=b1/B、二级丁坝相对长度ε2=b2/B、一级丁坝相对高度ψ1=D1/H0。回流参数包括回流长度、回流宽度、正负流区宽度比、回流曲线形态和回流流量等，下面基于水流数学模型的计算结果(计算工况见表1)，探讨阶梯形丁坝几何尺度ε1,ε2,ψ1和水流条件Fr对上述参数的影响规律，成果分析时在丁坝下游回流区每隔0.25 m布置一个统计断面，沿断面方向每隔0.10 m布置一条统计垂线，各垂线有9个流速点据。

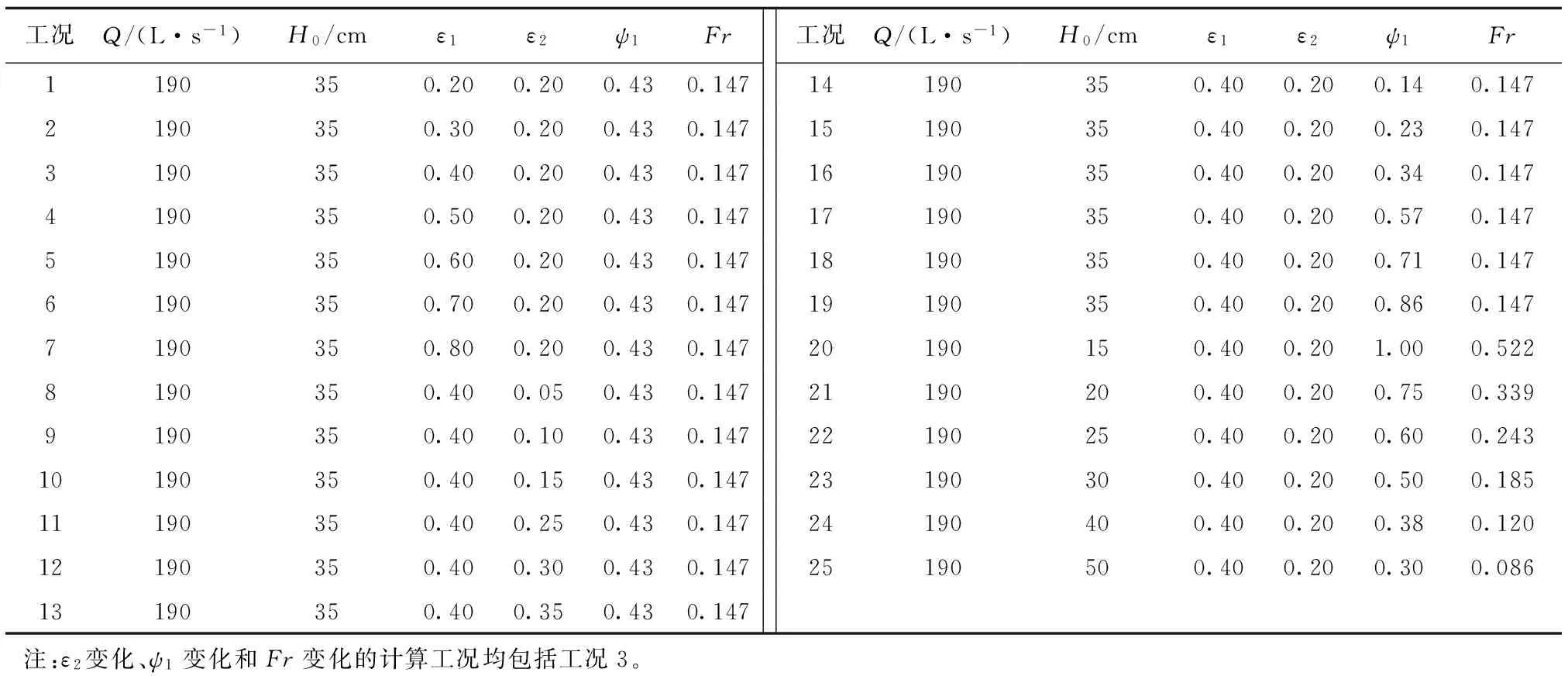
表1 水流数学模型计算工况Tab.1 Calculation condition of flow mathematical model

2.2.1回流长度 图6给出了ε1，ε2，ψ1和Fr对无量纲回流长度l/b2(l为回流长度)的影响规律。结果表明：①l/b2(或l/B)随ε1和ε2均呈递增变化，ε1，ε2越大，l/b2递增变化速度越缓，回流长度一般可达二级丁坝长度的20～30倍；②l/b2随ψ1也呈递增变化，ψ1越大，l/b2递增变化越明显，这主要因为一级丁坝长度大于二级丁坝，其高度增大后对坝后回流尺度的影响将更为突出；③ 由于ε1，ε2和ψ1的变化将改变河道糙率，丁坝回流长度与河道糙率有关[4]，因而l/b2将发生相应变化；④l/b2随Fr呈先增大后减小的趋势，l/b2最大值出现在Fr=0.35附近，比较而言，Fr对回流长度的影响较ε1，ε2，ψ1更不明显；⑤阶梯形丁坝回流长度随丁坝坝长的增大而增大、Fr对回流长度影响较小等变化规律与现有单式断面丁坝的研究结论[12]基本一致。

图6 回流长度随影响因素的变化Fig.6 Change of backflow region length with influencing factors

2.2.2回流宽度 图7给出了回流宽度参数(回流宽、正流宽和负流宽)最大值及平均值随ε1，ε2，ψ1和Fr的变化情况。图中显示：① 回流宽、正流宽和负流宽的最大值及平均值随ε1，ε2，ψ1和Fr的变化趋势总体一致；② 当ε1≤0.6时，回流宽度参数随ε1缓慢递增，当ε1>0.6时，回流宽度参数随ε1基本不变，最大回流宽约为二级丁坝宽度的1.5～2.0倍，与单式断面丁坝的研究结论[9]接近；③ 回流宽度参数b/B和b/b2随ε2呈现出相反的变化趋势，ε2越大，b/B越大，而b/b2越小，说明回流宽度随二级丁坝长度的增大而增大，但相对增幅逐渐递减；④ 当ψ1≤0.45时，回流宽度参数随ψ1基本不变，当ψ1>0.45时，回流宽度参数随ψ1先增大后减小，b/b2的最大值出现在ψ1=0.70附近；⑤ 最大回流宽度随Fr呈先增大后减小的趋势变化，平均回流宽度随Fr的变化相对较不明显。

图7 回流宽度随影响因素的变化Fig.7 Change of backflow region width with influencing factors

2.2.3正、负流区宽度比 图8给出了典型计算工况下回流正、负流区宽度比bz/bf随ε1，ε2，ψ1和Fr的变化趋势(图中bz和bf分别为各统计断面的回流正流区宽度和负流区宽度)，图中显示：①bz/bf沿程变化曲线总体为上凸状，多呈先增大、后基本稳定、再减小的变化过程；②bz/bf随ε2变化的波动相对较小，而随ε1，ψ1和Fr的波动相对略大；③bz/bf值一般小于1.0，说明负流区宽度相对更大，尤其在靠近丁坝的部位，负流区宽度可达正流区宽度的2.5倍。

图8 正、负流区宽度比随影响因素的变化Fig.8 Change of positive velocity region width and negative velocity region width with influencing factors

2.2.4回流曲线形态 图9给出了典型计算工况下的回流曲线形态随ε1,ε2,ψ1和Fr的变化趋势(图中x为沿程距离，b为各统计断面的回流宽度)，可见：① 与单式断面丁坝回流曲线形态[8]类似，阶梯形丁坝的回流曲线也呈纺锤状；② 随着ε1和ψ1的增大，回流曲线最大宽度变化不大，但回流长度逐渐增大，曲线形态逐渐被拉长；③ 不同ε2下的回流曲线差别明显，ε2越大，回流曲线长度和宽度也越大，说明ε2对回流曲线形态影响较大；④ 由于Fr对回流长度和宽度的影响均较小，回流曲线形态也随Fr的变化不大。

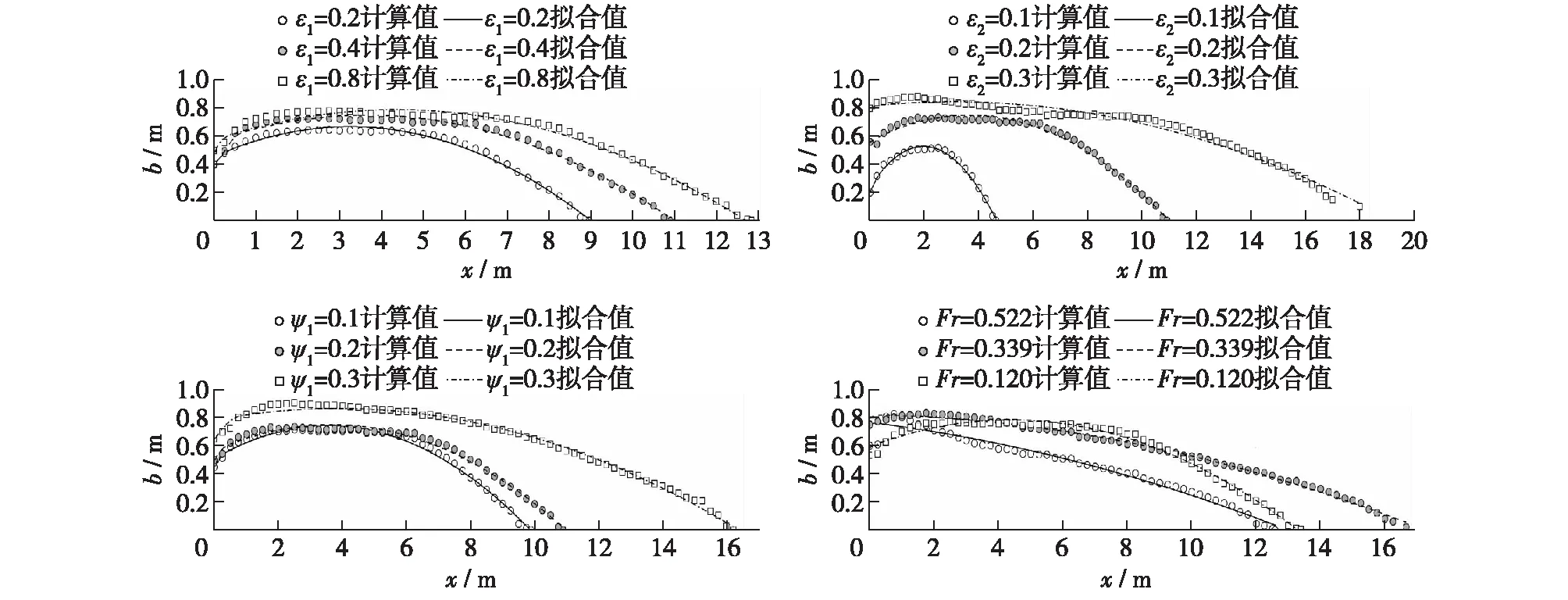
图9 回流曲线形态随影响因素的变化Fig.9 Change of backflow curve shape with influencing factors

2.2.5回流流量 根据沿程统计断面的垂线及流速点布置情况，可计算各垂线的分条流量Qi=BiHiUi，其中为Bi,Hi,Ui分别为分条宽度(Bi=0.10 m)、平均水深和纵向垂线平均流速，从丁坝对岸的右侧向丁坝侧分别计算分条流量Qi。当分条流量之和ΣQi等于上游来流量Q时，该垂线即为统计断面的回流区边界所在位置(实际计算时一般需由相邻两垂线线性内插ΣQi=Q的具体位置)；由于回流区正向流动和负向流动的流量之和为0，且各断面流量是闭合的，假定Qi>0的分条流量和为Q1，则回流流量QH=Q1-Q。根据上述方法，可计算各统计断面的回流流量。

图10给出了典型计算工况下相对回流流量QH/Q的沿程变化情况，结果表明：①QH/Q总体随ε1，ε2和ψ1的增大而增大，随Fr的增大而减小，各工况下QH/Q最大值多在0.04～0.10范围内变化，说明回流流量一般小于来流量的10%；② 紧邻丁坝下游端回流流量逐渐增大，为回流增流区，当达到最大值后，回流流量逐渐减小，为回流减流区，增流区和减流区的分界点沿程位置随ε1,ε2,ψ1和Fr的变化范围分别为(2.37～3.38), (1.24～4.64), (2.74～3.14)和(1.24～3.13)倍水槽宽度，说明ε1和ψ1对分界点沿程位置的影响较小，而ε2和Fr的影响较大；③回流流量沿程分布呈右偏的不对称曲线，增流区回流流量变化相对缓慢，而减流区变化相对剧烈。

图10 回流流量随影响因素的变化Fig.10 Change of circumfluence flow with influencing factors

3 结 语

阶梯形丁坝是常见的航道整治建筑物，应用三维水流数学模型并在模型验证的基础上，研究了阶梯形丁坝几何尺度及来流条件对回流规律的影响，主要认识如下：

(1)阶梯形丁坝回流长度随一级丁坝相对长度ε1及高度ψ1、二级丁坝相对长度ε2均呈递增趋势，随弗劳德数Fr呈先增后减的变化趋势，回流长度最大值出现在Fr=0.35附近。

(2)回流宽、正流宽和负流宽的特征值随ε1,ε2,ψ1和Fr的变化趋势总体一致；ε1≤0.6时回流宽度缓慢递增，此后基本不变；回流宽度随ε2的增大而增大，但相对增幅逐渐递减；ψ1≤0.45时回流宽度基本不变，ψ1>0.45时回流宽度随ψ1先增大后减小；最大回流宽度随Fr呈先增大后减小的趋势变化，平均回流宽度随Fr的变化相对较不明显。

(3)回流正、负流区宽度比沿程变化曲线总体为上凸状，多呈先增大、后基本稳定、再减小的变化过程，负流区宽度相对较大，在靠近丁坝部位可达正流区宽度的2.5倍。

(4)阶梯形丁坝的回流曲线呈纺锤状，ε1和ψ1主要影响回流曲线长度，ε2影响回流曲线的整体形态，而Fr对回流曲线形态影响较小。

(5)回流流量一般小于上游来流量的10%，沿程分布曲线不对称，增流区回流流量变化相对缓慢，而减流区变化相对剧烈。

[1] 周冠伦， 荣天富， 刘书伦， 等. 航道工程手册[M]. 北京： 人民交通出版社， 2004： 687- 688. (ZHOU Guanlun， RONG Tianfu， LIU Shulun， et al. Waterway engineering handbook[M]. Beijing: People’s Commumication Press， 2004： 687- 688. (in Chinese))

[2] 周鑫靖. 非淹没双级复式断面丁坝三维水流特性研究[D]. 重庆: 重庆交通大学， 2016. (ZHOU Xinjing. Three-dimensional flow characteristics of non-submerged spur dike with two-stage compound section[D]. Chongqing: Chongqing Jiaotong University， 2016. (in Chinese))

[3] 冯永忠. 错口丁坝回流尺度的研究[J]. 河海大学学报， 1995， 23(4)： 69- 76. (FENG Yongzhong. Study on recirculating flow range caused by groins lying alternately[J]. Journal of Hohai University， 1995， 23(4)： 69- 76. (in Chinese))

[4] 李国斌， 韩信， 傅津先. 非淹没丁坝下游回流长度及最大回流宽度研究[J]. 泥沙研究， 2001(3)： 68- 73. (LI Guobin， HAN Xin， FU Jinxian. Study on the length and maximum width of the circulating region caused by a dike[J]. Journal of Sediment Research， 2001(3)： 68- 73. (in Chinese))

[5] 韩玉芳， 陈志昌. 丁坝回流长度的变化[J]. 水利水运工程学报， 2004(3)： 33- 36. (HAN Yufang， CHEN Zhichang. Variation of re-circulation length of spur dikes[J]. Hydro-Science and Engineering， 2004(3)： 33- 36. (in Chinese))

[6] ETTEMA R, MUSTE M. Scale effects in flume experiments on flow around a spur dike in flat bed channel[J]. Journal of Hydraulic Engineering， 2004， 130(7)： 635- 646.

[7] SHARMA K, MOHAPATRA P K. Separation zone in flow past a spur dyke on rigid bed meandering channel[J]. Journal of Hydraulic Engineering， 2013， 138(10)： 897- 901.

[8] 陈稚聪， 黑鹏飞， 丁翔. 丁坝回流分区机理及回流尺度流量试验研究[J]. 水科学进展， 2008， 19(5)： 613- 617. (CHEN Zhicong， HEI Pengfei， DING Xiang. Division and flow scale investigation of circulation zone around spur dike[J]. Advances in Water Science， 2008， 19(5)： 613- 617. (in Chinese))

[9] 郑艳， 魏文礼， 刘玉玲. 丁坝长度对回流长度影响的数值模拟研究[J]. 沈阳农业大学学报， 2014， 45(2)： 195- 199. (ZHENG Yan， WEI Wenli， LIU Yuling. Influence of spur-dike length on the recirculation scale by numerical simulation[J]. Journal of Shenyang Agricultural University， 2014， 45(2)： 195- 199. (in Chinese))

[10] 马永军， 陈稚聪， 丁翔. 控制和减小丁坝下游回流影响的实验[J]. 清华大学学报(自然科学版)， 2003， 43(8)： 1096- 1099. (MA Yongjun， CHEN Zhicong， DING Xiang. Controlling recirculating regions downstream of spur dikes[J]. Journal of Tsinghua University(Science and Technology)， 2003， 43(8)： 1096- 1099. (in Chinese))

[11] 马永军， 陈稚聪， 丁翔. 吸、喷水法减小丁坝下游回流尺度的试验研究[J]. 水科学进展， 2003， 14(6)： 763- 768. (MA Yongjun， CHEN Zhicong， DING Xiang. Experimental study on reducing the size of circulating region in the downstream of spur dikes[J]. Advances in Water Science， 2003， 14(6)： 763- 768. (in Chinese))

[12] 窦国仁. 丁坝回流及其相似律的研究[J]. 水利水运科技情报， 1978(3)： 1- 24. (DOU Guoren. An investigation on the whirlpool flow and its similarity laws[J]. Information of Hydro-Science and Engineering， 1978(3)： 1- 24. (in Chinese))

Analysisonlawofbackflowaroundstep-shapedspurdike

ZHONG Liang1, 2， SUN Jianyun2， LIU Junjie2， ZHOU Xinjing3

(1.NationalEngineeringResearchCenterforInlandWaterwayRegulation,ChongqingJiaotongUniversity，Chongqing400074，China； 2.KeyLaboratoryofHydraulicandWaterwayEngineeringoftheMinistryofEducation,ChongqingJiaotongUniversity，Chongqing400074，China； 3.ChongqingInformationandCommunicationConsultingandDesignInstituteCo.,Ltd.，Chongqing400041，China)

Step-shaped spur dike is widely used in the waterway regulation, and the law governing the backflow is closely related with the problems such as ship navigation, siltation of dam field(deposition between two groins) and embankment stability, but few studies are conducted in this field. In this research, the influence of spur’s geometric scale and inflow condition on the backflow is studied by using a three dimensional mathematical model of water flow. The results show that: ①The backflow region length increases with the increasing of the relative lengthε1and relative heightψ1of the first stage spur dike and the relative lengthε2of the second stage spur dike, and it increases first and then decreases with the Froude numberFr; ②The backflow region width changes relatively obviously withε1,ε2andψ1, and changes little withFroverall; ③The width ratio curve of the positive velocity region and the negative velocity region is overall convex, and the negative flow width is relatively large, which can be 2.5 times the width of the positive velocity region near the spur dike; ④The shape of backflow curve is related toε1,ε2andψ1, andε1andψ1mainly affect the length, whileε2affects the overall shape; ⑤The circumfluence flow is less than 10% of the discharge, and its distribution curve is asymmetric, with slow change in the flow increasing area and relatively severe change in the flow decreasing area.

step-shaped spur dike； size of backflow region； backflow curve； backflow discharge

U617.9； TV131. 2

A

1009-640X(2017)05-0009-09

10.16198/j.cnki.1009-640X.2017.05.002

钟亮， 孙建云， 刘珺洁， 等. 阶梯形丁坝下游回流规律分析[J]. 水利水运工程学报, 2017(5): 9-17. (ZHONG Liang, SUN Jianyun, LIU Junjie, et al. Analysis on law of backflow around step-shaped spur dike[J]. Hydro-Science and Engineering, 2017(5): 9-17. (in Chinese))

2016-11-12

重庆市基础与前沿研究计划项目(cstc2017jcyAX0278)； 国家自然科学基金资助项目(51509026)

钟 亮(1980—)， 男， 江西赣州人， 副教授， 博士， 主要从事航道整治理论与技术研究。

E-mail： zlcqjtu@163.com