洛伦兹系数在储层非均质性评价中的应用

， ，， ，，

(1.山东科技大学 地球科学与工程学院，山东 青岛 266590；2.中国石化江苏油田分公司 第二采油厂，江苏 淮安 223000)

洛伦兹系数在储层非均质性评价中的应用

郑晨晨1，谢俊1，王金凯1，赵璇1，段雅君1，孙燕2

(1.山东科技大学 地球科学与工程学院，山东 青岛 266590；2.中国石化江苏油田分公司 第二采油厂，江苏 淮安 223000)

针对目前油气储层宏观非均质性评价参数众多、评价指标无边界的问题，以江苏金湖凹陷王龙庄油田为例，综合运用岩心观察、室内分析试验和测井解释等资料，通过计算岩石样品的渗透率洛伦兹系数对研究区阜宁组二段储层层内和平面非均质性进行研究。洛伦兹系数为0～1的数值，可以作为评价储层非均质程度的指标，从而定量评价储层的宏观非均质性。结果表明，洛伦兹系数能够弥补传统储层非均质性评价指标无边界的问题，可在其他地区的储层宏观非均质性评价中进行推广。

非均质性；洛伦兹系数；低渗透储层；王龙庄油田

储层非均质性研究是储层评价的核心内容，也是影响油气水分布及注水开发的重要因素，在低渗透油田中尤其重要[1]。目前，碎屑岩储层非均质性研究在层序地层学、地质统计学、地质建模等方面取得了一些进展，但主要还是通过计算渗透率变异系数Vk、突进系数Tk、级差Jk等参数进行表征[2]。采用上述参数从不同角度对储层的层内非均质性进行评价，但这些数值的计算在理论上都是无界的，不能对储层的非均质程度进行定量评价。目前的解决办法是将这些数值定性分成三个区间(弱非均质性、中等非均质性及严重非均质性)，从而大致描述储层的层内非均质性级别[3-5]。所以传统的手段无法定量描述储层的非均质程度。

洛伦兹系数又称基尼系数，最早由意大利经济学家基尼[5-6]提出，原是经济学判断收入分配是否均衡的指标，后被石油地质学家用来定量描述储层非均质性。如岳崇旺等[2]利用洛伦兹系数识别和评价储层非均质性；Peter等[7]将其引入碳酸盐岩储层的非均质性评价中；刘超等[8]对洛伦兹系数评价储层非均质性的方法进行改进；王庆等[9]利用洛伦兹系数研究油藏的产液、吸水剖面。该方法多利用测井曲线计算洛伦兹系数。本次研究结合取心井岩心样品数据和常规测井资料，计算渗透率洛伦兹系数来评价储层的非均质程度，实现对储层非均质性的定量评价。

1 地质概况

王龙庄油田位于苏北盆地金湖凹陷汊涧次凹东侧，物源来自西侧的张八岭隆起[10]，是一系列断鼻构造组成的断块群(图1)。研究区王龙庄断块位于王龙庄油田西南方向，该区主要含油层位为阜宁组二段(以下简称阜二段)，地质储量116×104t。按研究区原有油矿地质学划分，阜二段自上而下共分为Ⅰ、Ⅱ、Ⅲ三个砂组，Ⅱ、Ⅲ砂组为主要研究层位，Ⅱ砂组发育2个含油小层，Ⅲ砂组发育7个含油小层。王龙庄断块阜二段储层平均渗透率为20.13×10-3μm2，按照碎屑岩储层分类标准[11]属于低渗透储层，本次主要应用洛伦兹系数法研究低渗透储层非均质性。

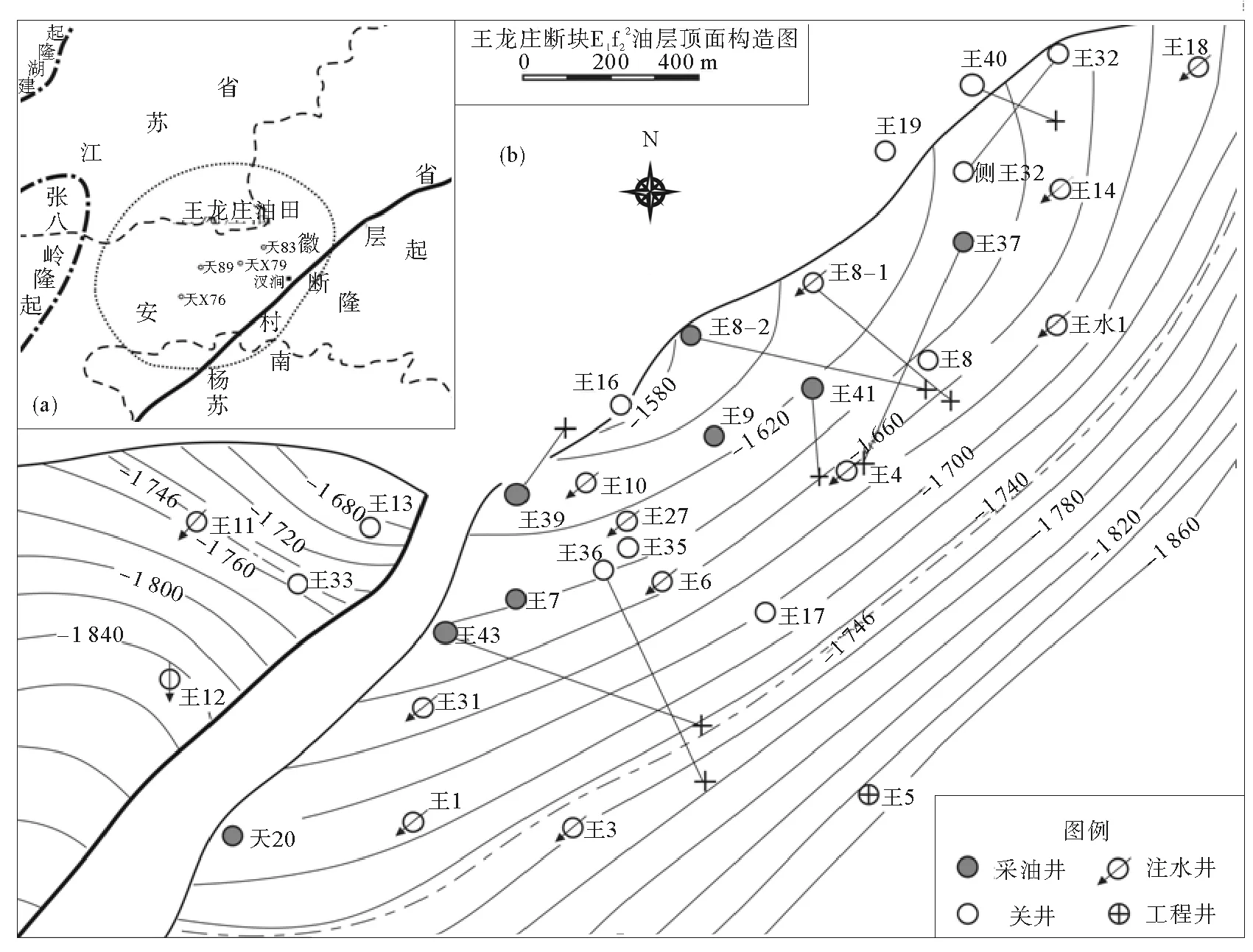
图1 金湖凹陷王龙庄断块区域位置图Fig.1 Location map of Wanglongzhuang-fault-block in Jinhu Depression

2 洛伦兹系数计算原理

洛伦兹系数法是采用储层岩石样品的实际渗透率贡献值曲线和理想储层绝对均质曲线之间的面积与储层绝对均质曲线和纵坐标轴围成面积的比值来表示储层的非均质程度[12]。因此，绘制洛伦兹曲线的前提是求取岩样渗透率贡献值累积百分数，计算步骤如下：

1) 将研究区储层的渗透率值由大到小按降序排列，保证计算渗透率贡献值累积百分数从大到小开始累积。

2) 利用公式(1)、(2)计算每一块岩石样品的渗透率贡献值累积百分数。

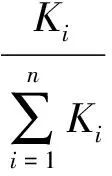
(1)

其中：Li为第i个岩石样品所对应的渗透率值对整体渗透率，%；Ki为第i个岩石样品所对应的渗透率值，10-3μm2；n为此次研究所用岩石样品的总个数。

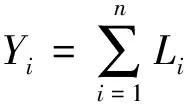
(2)

其中：Yi为第i个岩石样品所对应的渗透率贡献值累积百分数，%。

3) 同理，可以利用公式(3)和(4)求出每一块岩石样品的岩样累积百分数。

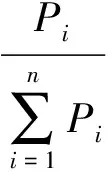
(3)

(4)

其中，Qi为第i个岩石样品对整体的贡献值，%；Pi为第i个岩石样品；n为此次研究所用岩石样品的总个数；Xi为第i个岩石样品所对应的岩样累积百分数，%。

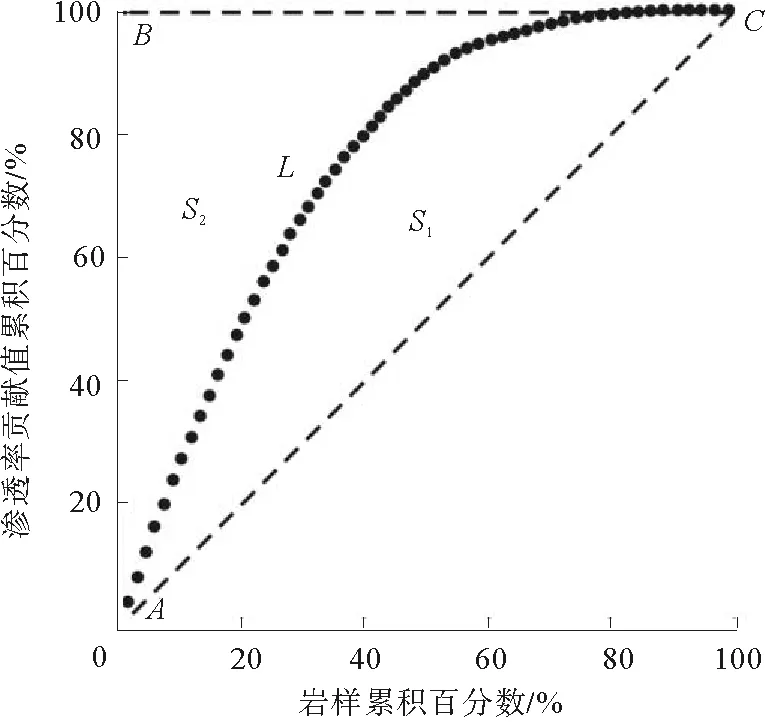
图2 渗透率洛伦兹曲线Fig. 2 Lorentz curve of permeability

将求出的岩样渗透率贡献值累积百分数和岩样累积百分数(Xi，Yi)放在直角坐标系中得到相应储层的洛伦兹曲线(图2)。对于完全均质的储层，洛伦兹曲线应为一条直线Y=X(图2，AC)，表示储层中每一个数据点的渗透率值相等；而对于极端非均质的储层，洛伦兹曲线为一条折线(图2，ABC)，表示储层渗透率差异非常大；通常情况下，储层渗透率洛伦兹曲线分布于两者之间，为一条呈上凸形态的曲线(图2，L)。

设洛伦兹曲线L与储层绝对均质曲线AC所围成的面积为S1，绝对均质曲线AC与极端非均质曲线ABC所围成的面积为(S1+S2)，则洛伦兹系数即为S1/(S1+S2)。其中，完全均质储层的洛伦兹系数为0，极端非均质储层的洛伦兹系数为1，常规储层渗透率洛伦兹系数在0～1之间。因此，洛伦兹系数可以作为储层的非均质程度系数，以此定量评价储层的宏观非均质程度。

3 储层非均质性评价

根据研究目的、储层非均质性可有多种分类方法，其中裘亦楠(1992)[13]将碎屑岩的储层非均质性划分为层内、层间、平面和孔隙非均质性四类，其中储层宏观非均质性研究主要从层内、层间以及平面三方面着手。沉积因素是影响储层非均质性的最根本因素，因不同沉积环境沉积时水体能量、沉积物的性质(粒度、成分、分选性、磨圆度)等不同，导致储层内部沉积结构和构造的各向异性，从而造成储层非均质程度的差别[14]。本研究从沉积微相划分入手，利用洛伦兹系数评价储层的层内和平面非均质性。

3.1 层内非均质性评价

储层的层内非均质性是指各小层内的储层特征变换，分别运用传统的变异系数法和洛伦兹系数法对研究区储层的层内非均质性进行评价。

3.1.1 变异系数法

根据王龙庄断块33口井的测井数据，结合6口取心井的岩心资料综合分析，建立回归公式，对研究区各井的孔渗数据进行校正，分别计算每口井阜二段Ⅱ、Ⅲ砂组中7个主要含油层系的变异系数、突进系数等数值(表1)。

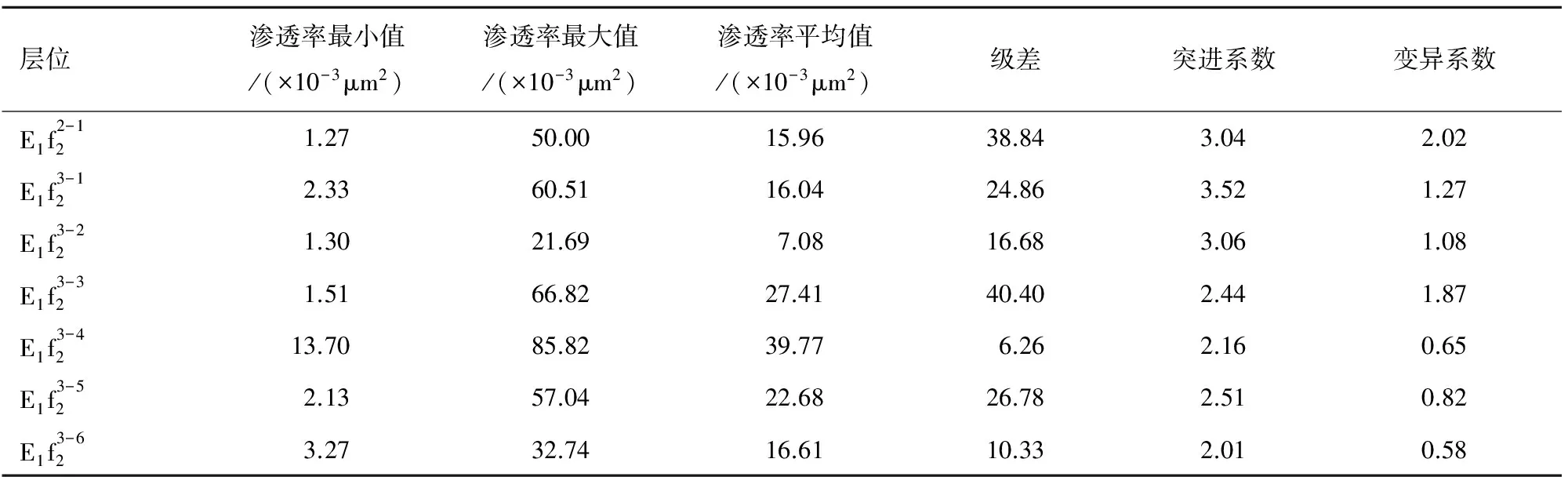
表1 王龙庄断块阜二段层内变异系数统计Tab.1 Statistics of variation coefficient in the E1f2 of Wanglongzhuang-fault-block

3.1.2 洛伦兹系数法

表2 王龙庄断块阜二段层内洛伦兹系数统计Tab.2 Statistics of Lorentz coefficient in the E1f2 of Wanglongzhuang-fault-block

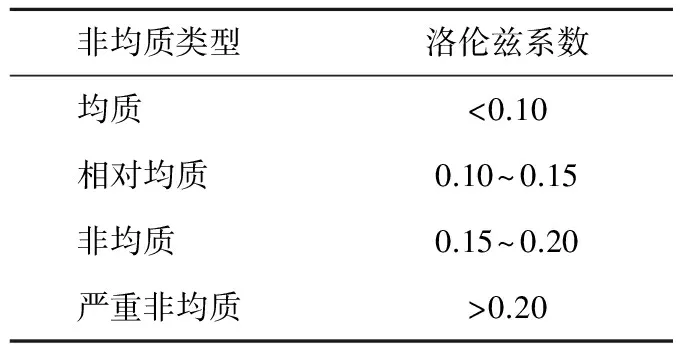
表3 王龙庄断块储层非均质性洛伦兹系数评价标准Tab. 3 Reservoir heterogeneity evaluation standard of Lorentz coefficient in Wanglongzhuang-fault-block

由表2、表3可以看出，研究区各小层洛伦兹系数0.27～0.51，与变异系数呈正比，属严重非均质性。洛伦兹系数取值在0(完全均质)到1(极端非均质)之间，可以作为储层非均质程度系数来描述储层的非均质程度。

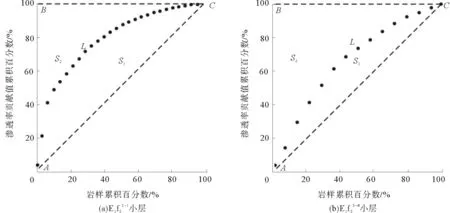
图3 王龙庄断块渗透率洛伦兹曲线Fig.3 Permeability Lorentz curve of Wanglongzhuang-fault-block

此外，不同沉积环境控制下储层的韵律性不同，而不同的韵律性将导致储层物性纵向上的差异[15]。研究区主要为滨浅湖滩坝沉积，由于沉积过程受湖浪的频繁改造，具有反韵律、正韵律及复合韵律多种韵律模式。通过单井纵向测井曲线、渗透率分布，研究区主要以反韵律为主，细砂岩或粉砂岩与泥岩频繁互层，层内渗透率变化较大、导致层内非均质性严重(图4)。

两种方法对比与应用可以发现，相比于变异系数法，洛伦兹系数法具有以下优点：①数值计算有界，能够作为储层非均质程度系数使用，可以定量评价储层的非均质性；②可以克服传统方法各参数表征角度各异的问题，作为统一评价非均质程度的标准；③结合洛伦兹曲线使得结论更加简洁、直观。

3.2 平面非均质性评价

平面非均质性是指各小层渗透率在平面上的变化情况，由于不同沉积微相在平面上的分布不同所表现出的不同物性特征，可以从沉积微相平面分布、渗透率平面分布等反映出来[16]。目前广泛采用的渗透率等值线图虽然可以直观展示平面非均质性变化的特点，但依然难以定量评价平面非均质程度，结合洛伦兹系数可以解决这一难题。

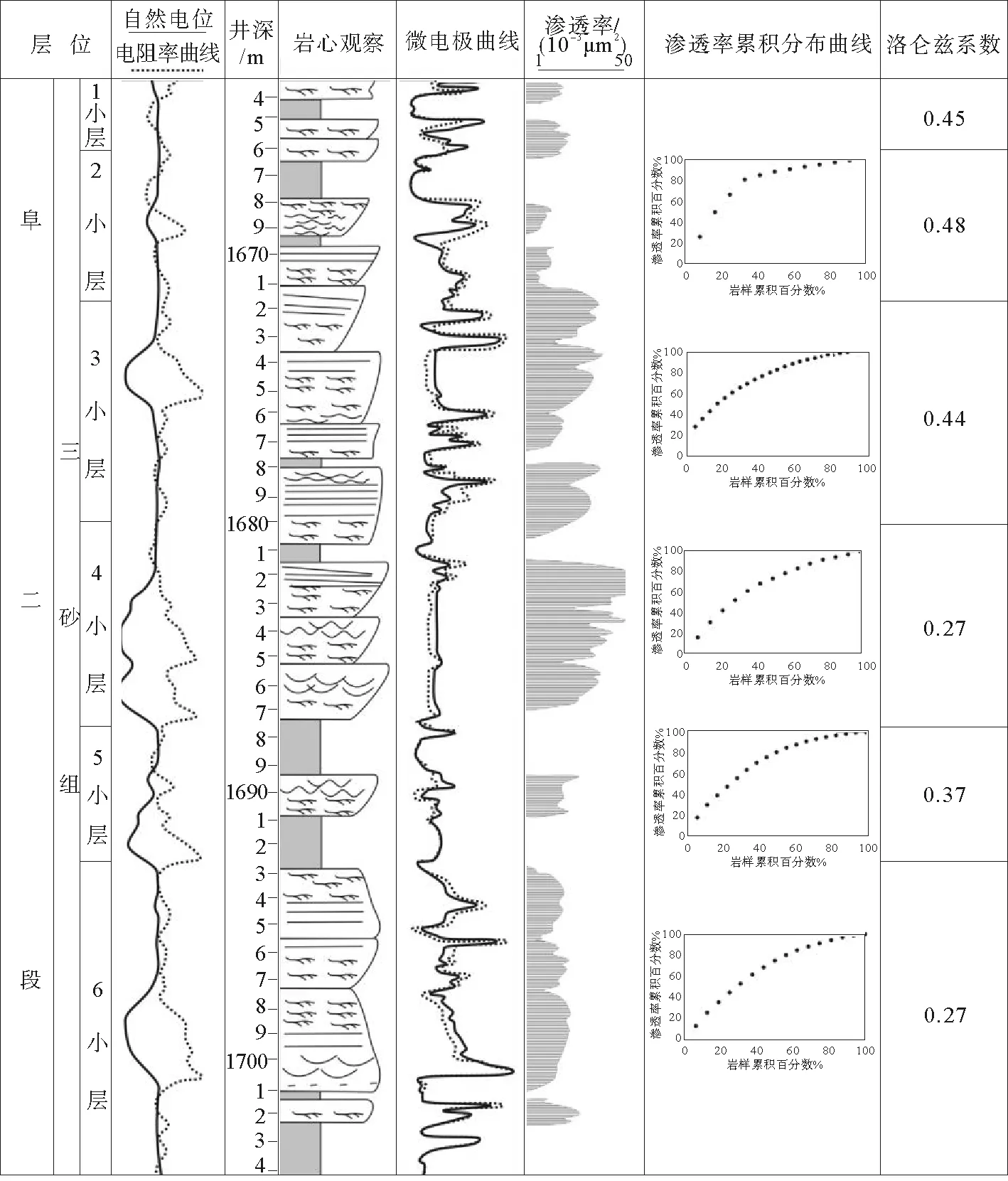
图4 王龙庄断块阜二段Ⅲ砂组层内非均质性定量表征(W10井)Fig. 4 Quantitative characterization of the inlayer heterogeneity of the 3rd sand sets in the second member of Funing formation in Wanglongzhuang-fault-block (well W10)

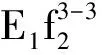
3.3 结果评价及措施

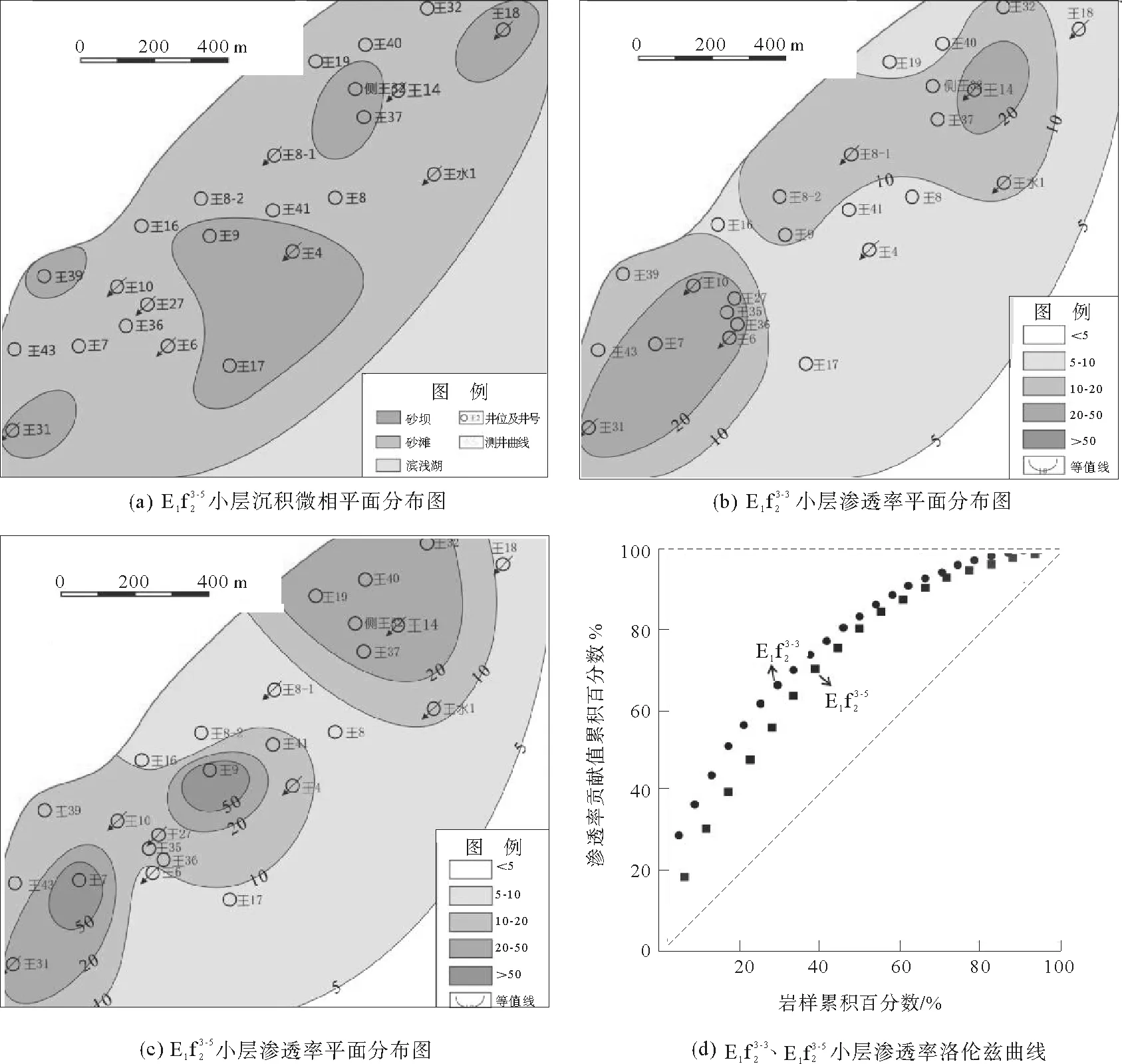
图5 王龙庄断块阜二段小层平面非均质性定量表征Fig.5 Quantitative characterization of the plane heterogeneity of E1 and E1 layers in Wanglongzhuang-fault-block

4 结论

1) 洛伦兹系数是在储层渗透率累积百分数基础上计算出的一种新参数，与变异系数法相比具有定量化、结论直观和计算简便等优点；洛伦兹系数的引入可以完善目前储层非均质性评价体系，为储层非均质程度提供了统一的标准，改变了以往评价方法中缺乏统一评价指标的问题。

2) 以王龙庄断块阜二段储层渗透率参数为基础，结合储层层内韵律性变化，利用洛伦兹系数法对研究区储层层内非均质程度进行评价，结果显示研究区储层洛伦兹系数在0.27～0.51，非均质程度严重；研究区发育滨浅湖滩坝沉积，沙滩砂体物性较差但分布广泛，沙坝砂体物性较好但零星分布，导致储层平面非均质程度严重。

3) 洛伦兹系数法在王龙庄断块储层非均质性评价中效果较好，评价结果与现场生产实践相吻合，可以在其他类似油田推广应用。

[1]张金亮,谢俊.油田开发地质学[M].北京：石油工业出版社,2011:142-153.

[2]岳崇旺,杨小明,钟晓勤,等.利用测井曲线的洛伦兹系数评价地层的非均质性[J].吉林大学学报(地球科学版),2015,45(5):1539-1546.

YUE Chongwang,YANG Xiaoming,ZHONG Xiaoqin,et al.Evaluation of formation heterogeneity using Lorentz coefficient of logging curves[J].Journal of Jilin University (Earth Science Edition),2015,45(5):1539-1546.

[3]严科,杨少春,任怀强.储层宏观非均质性定量表征研究[J].石油学报,2008,29(6):870-874.

YAN Ke,YANG Shaochun,REN Huaiqiang.Research on quantitative characterization of macroscopic heterogeneity of reservoir[J].Acta Petrolei Sinica,2008,29(6):870-874.

[4]罗晓容,王忠楠,雷裕红,等.特超低渗砂岩油藏储层非均质性特征与成藏模式:以鄂尔多斯盆地西部延长组下组合为例[J].石油学报,2016,37(增1):87-98.

LUO Xiaorong,WANG Zhongnan,LEI Yuhong,et al.Heterogeneity characteristics and accumulation model of ultra-low permeability sandstone reservoirs:A case study of the lower part of Yanchang formation in the western Ordos Basin,China[J].Acta Petrolei Sinica,2016,37(S1):87-98.

[5]游士兵,王原君.研究收入分配问题的一种新洛伦兹曲线模型:建构与应用[J].经济评论,2014(2):3-15.

YOU Shibing,WANG Yuanjun.A new Lorenz model for income distribution analysis:Model construction and application[J].Economic Review,2014,(2):3-15.

[6]何邦强,洪兴健.基尼系数计算与分解方法研究综述[J].统计与决策,2016,14:13-17.

HE Bangqiang,HONG Xingjian.A review of Gini coefficient calculation and decomposition[J].Statistics & Decision,2016,14:13-17.

[7]FITCH P,DAVIES S,LOVELL M,et al.Heterogeneity in carbonate petrophysical properties:Application to fluid flow units and sampling strategies[C]//SPWLA 51st Annual Logging Symposium.Xi’an:CNPC Logging,2010:19-23.

[8]刘超,马奎前,李红英,等.基于洛伦兹曲线法定量表征储层非均质性方法的改进与应用[J].中国海上油气,2012,24(2):36-38.

LIU Chao,MA Kuiqiang,LI Hongying，et al.An improvement of quantitative reservoir-heterogeneity characterization based on Lorenz curve method and its application[J].China Offshore Oil and Gas,2012,24(2):36-38.

[9]王庆,刘慧卿,殷方好.洛伦兹曲线在油藏产液、吸水剖面研究中的应用[J].特种油气藏,2010,17(1):71-74.

WANG Qing,LIU Huiqing,YIN Fanghao.Application of Lorenz curve to the study of production profile and injection profile[J].Special Oil and Gas Reservoirs,2010,17(1):71-74.

[10]丁玉盛,周巨标,石先达,等.王龙庄油田阜宁组二段碳酸盐与碎屑岩混合沉积滩坝体系[J].山东科技大学学报(自然科学版),2015,34(2):58-63.

DING Yusheng,ZHOU Jubiao,SHI Xianda,et al.Beach bar system mixed carbonate and siliciclastic sediments in the second member of Funing formation in Wanglongzhuang oilfield[J].Journal of Shandong University of Science and Techno-logy(Natural Science),2015,34(2):58-63.

[11]中华人民共和国地质矿产行业标准.DZ/T0217-2005,石油天然气储量计算规范[S].

[12]马玉玲.劳伦兹方法在储层非均质评价中的应用[J].长江大学学报(自然科学版),2013,10(10):90-91.

MA Yuling.Application of Lorenz method in the evaluation of reservoir heterogeneity[J].Journal of Yangtze University(Nature Science Edition),2013,10(10):90-91.

[13]裘亦楠.中国陆相碎屑岩储层沉积学的进展[J].沉积学报,1992,10(3):16-24.

QIU Yinan.Developments in reservoir sedimentology of continental clastic rocks in China[J].Acta Sedimentologica Sinica,1992,10(3):16-24.

[14]孟宁宁,刘怀山,张金亮,等.黑46断块低渗油藏非均质性研究及其对剩余油分布的影响[J].海洋地质与第四纪地质,2016,36(1):143-150.

MENG Ningning,LIU Huaishan,ZHANG Jinliang,et al.Heterogeneity and its impact on remaining oil distribution of low-permeability reservoirs in the HEI46-Block[J].Marine Geology & Quaternary Geology,2016,36(1):143-150.

[15]中华人民共和国石油天然气行业标准.SY/T5717-95,单井碎屑岩储层评价[S].

[16]张世广,卢双舫,张雁,等.高分辨率层序地层学在储层宏观非均质性研究中的应用:以松辽盆地朝阳沟油田朝1-朝气3区块扶余油层为例[J].沉积学报,2009,27(3):458-469.

ZHANG Shiguang,LU Shuangfang,ZHANG Yan,et al.Application of high-resolution sequence stratigraphy in the study of the reservoir macro-heterogeneity:Taking the Fuyu oil layer of Chao1-Chaoqi3-Blocks in Chaoyanggou oil reservoir of Songliao basin as an example[J].Acta Sedimentologica Sinica,2009,27(3):458-469.

ApplicationofLorentzCoefficientinReservoirHeterogeneityEvaluation

ZHENG Chenchen1, XIE Jun1, WANG Jinkai1, ZHAO Xuan1, DUAN Yajun1, SUN Yan2

(1. College of Earth Science and Engineering, Shandong University of Science and Technology, Qingdao, Shandong 266590, China; 2. Second Oil Production Plant of Jiangsu Oilfield Company, SINOPEC, Huai′an, Jiangsu 223000, China)

There are some defects in the existing evaluation systems of macroscopic heterogeneity such as the great number and unboundedness of evaluation parameters. Taking Wanglongzhuang Oilfield in Jinhu Depression, Jiangsu province as an example, this paper studied the reservoir layers and plane heterogeneity of the second number of Funing formation through the calculation of Lorentz coefficient of rock samples’ permeability in the study area based on core observation, laboratory analysis and logging interpretation. Lorentz coefficient value 0-1 can be used as the evaluation index of reservoir heterogeneity degree so as to make quantitative evaluations of the reservoir’s macro-scopic heterogeneity. Application results show that Lorentz coefficient can make up for the unboundedness of traditional reservoir hetero-geneity evaluation indexes and can be extended to the evaluation of reservoir’s macroscopic heterogeneity in other places.

heterogeneity； Lorentz coefficient; low permeability reservoir； Wanglongzhuang Oilfield

郑晨晨,谢俊,王金凯,等.洛伦兹系数在储层非均质性评价中的应用[J].山东科技大学学报(自然科学版),2018,37(1):103-110.

2016-11-29

国家自然科学基金项目(51674156，51504143)

郑晨晨(1992—)，男，山东济宁人，硕士研究生，主要从事油气田开发方面的研究.E-mail：441760455@qq.com

谢 俊(1968—)，男，湖北京山人，教授，博士生导师，主要从事油气储层评价与油藏描述方面的研究，本文通信作者.E-mail：xiejun0532@163.com

ZHENG Chenchen, XIE Jun, WANG Jinkai,et al. Application of Lorentz coefficient in reservoir heterogeneity evaluation[J].Journal of Shandong University of Science and Technology(Natural Science),2018,37(1):103-110.

TE348

A

1672-3767(2018)01-0103-08

10.16452/j.cnki.sdkjzk.2018.01.010

吕海亮)