浅析市政工程中总输电区位置的确定

王 瑞,李兆峰,燕相臣,曾梦圆

（山东交通职业学院 公路与建筑学院,山东 潍坊 261206）

浅析市政工程中总输电区位置的确定

王 瑞,李兆峰,燕相臣,曾梦圆

（山东交通职业学院 公路与建筑学院,山东 潍坊 261206）

为确定市政工程中总输电区位置确定，使得在输电规定范围内输电线路最短，本文利用Floyd算法来解决。

Floyd算法；邻接矩阵；总输电区；Matlab

0 前言

市政设施是指在城市区、镇（乡）规划建设范围内设置、基于政府责任和义务为居民提供有偿或无偿公共产品和服务的各种建筑物、构筑物、设备等。其中，电力输送就是重要的一部分，但在总输电区向受电区输电时，确定总输电区的位置是一个关键的问题，因为关系到经济、线路磨损等问题，在规定输电范围内，只要输电线路最短，那该方面经济、线路磨损等问题会相应减弱。解决这一问题的方法有很多，如：Floyd算法、Dijkstra算法等，本文利用Floyd算法对这一问题进行思考。

1 Floyd算法介绍

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。它的基本思想是直接在图的带权邻接矩阵中用插入顶点的方法依次构造出v个矩阵D(1)，D(2)，D(3)，...，D(v)，使D(v)成为图的距离矩阵，同时也求出插入点矩阵以便得到两点间的最短路径，本方法可以用Matlab进行解决。

2 总输电区位置的确定过程

（3）求出各点vi设立总输电区的最大线路距离 M (vi)：

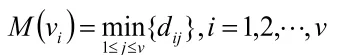
（4）求出顶点vk，使所以vk就是所求总输电区的位置。

3 实例分析

某地区进行输电工程，要在七处分地区确定一处总输电区的位置，现根据分地区的布局如图1所示，其中地区与地区之间数值表示距离，以此按上述方法进行总输电区位置的确定。

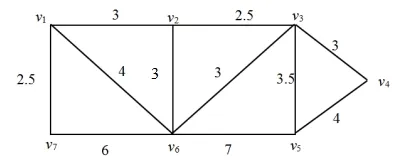
图1 分地区布局图

首先确定其邻接矩阵如下：

利用Matlab进行编程得到以下数据，如图2、3：

图2 关于D的矩阵

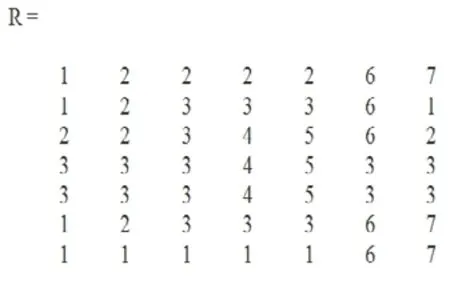
图3 关于R的矩阵

4 结论

利用Floyd算法准确有效，能较快的确定总输电区的位置,但存在一定的缺陷，如果确定总输电区的位置在加入不可控因素，特指影响因素较多的情况下，对此算法增加复杂性，因此在研究此类问题时需要更加完善此算法。

[1]赵静，但琦等.数学建模与数学实验[J].北京：高等教育出版社，2014.

[2]郝自军,何尚录.最短路问题的Floyd算法的若干讨论[J].重庆工学院学报(自然科学版),2008(05):156-159.[2017-09-02].

10.16640/j.cnki.37-1222/t.2018.01.082