水蒸气流量测量的温度压力补偿计算
刘翠凤, 张育玮, 孔祥翠
(中国寰球工程公司 新疆分公司,新疆 克拉玛依 833699)
水蒸气流量测量的温度压力补偿计算
刘翠凤, 张育玮, 孔祥翠
(中国寰球工程公司 新疆分公司,新疆 克拉玛依 833699)
介绍了水蒸气流量测量温压补偿的2种方法及流量温压补偿的原理,通过研究水蒸气密度的计算方法,对比分析计算误差,给出了计算水蒸气密度的推荐公式,并由此得出水蒸气流量测量的温压补偿计算公式。同时研究了过热水蒸气压缩系数的2种计算方法,利用Matlab编制计算程序,给出了计算压缩系数的推荐公式,探讨了实际气体状态方程是否适用于水蒸气的问题。
过热水蒸气 饱和水蒸气 温压补偿 密度 压缩系数
水蒸气作为石油化工领域中十分常见的一种介质,其流量测量与密度有着不可分割的联系。水蒸气流量测量的温压补偿一般有2种方法:一种方法是智能仪表自带温度和压力补偿计算流量软件,但费用较高;另一种方法是在DCS或PLC等控制系统组态中,利用温度和压力的测量值实时计算密度值,再对流量进行校正,节省费用。本文主要研究了第二种方法。
1 流量的温压补偿原理
差压式流量仪表[1]如孔板、喷嘴、均速管、楔形流量计,其测量值与密度的关系可用式(1)表示,靶式流量计的测量值与密度的关系可用式(2)表示,浮子流量计的测量值与密度的关系可用式(3)表示,速度式流量仪表如涡街流量计,其测量值与密度的关系可用式(4)表示[2]。

(1)

(2)
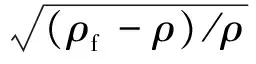
(3)
qm=ρvS
(4)
式中:qm——质量流量,kg/s;ki——流量系数,i=1,2,3;Δp——差压,Pa;ρ——流体的密度,kg/m3;F——靶式流量计中流体对靶的作用力;ρf——浮子流量计中浮子的密度,kg/m3;v——速度式流量计中流体的平均流速,m/s;S——通道截面积,m2。
1)ρ是压力与温度的二元函数,如式(5)所示。在实际生产中,由于流体的操作压力和温度并不是固定不变的,因而使用固定的ρ值计算出的流量值有较大偏差,必须采取有效的温压补偿措施。
ρ=f(p,T)
(5)
式中:p——压力,Pa;T——温度,K。
2) 流量的温压补偿原理是利用实时检测的温度和压力值计算流体的实际密度,再利用该密度值重新计算流量。由式(1)和(2)可知,流量的温压补偿公式可用式(6)表示,对于式(3),可用式(7)表示,对于式(4),可用式(8)表示。

(6)
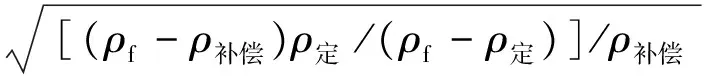
(7)
qm补偿=qm测ρ补偿/ρ定
(8)
式中:qm补偿——经过温压补偿后的质量流量计算值,kg/s;qm测——未经过温压补偿的质量流量测量值,kg/s;ρ补偿——经过温压补偿后的密度值,kg/m3;ρ定——给定的密度值,即不带温压补偿的仪表计算流量所使用的密度值,kg/m3。
由此可知,通过一定方法获得准确的流体密度是流量的温压补偿算法的核心。
2 过热水蒸气流量的温压补偿
过热水蒸气的密度共有6种常见计算方法。
2.1 查表法
由于过热水蒸气的密度是温度和压力的二元函数,因此最关键的是求取该二元函数。早在1967年国际水和水蒸气热力性质协会(IAPWS)[3-4]已经提出了详细的计算方法,并于1997年修正了该计算标准,但由于该公式极为复杂,故实际上一般应用是根据上述计算标准列出的过热水蒸气密度表。过热水蒸气密度表中的数据是通过实验测得的,通常可认为该数据为过热水蒸气的真实密度值。该法的数据存储量较大,且表中未列出的数据需要通过二次插值拟合计算,通常只用于手工查找。
2.2 实际气体状态方程
实际气体的状态方程[5]如式(9)所示:
ρ=p/ZRT
(9)
式中:R——气体常数,R=461 J/(kg·K);Z——气体压缩系数。
其中的Z可利用Redlich-Kwong(雷德利克-孔)[5]方程求解,如式(10):
Z3-Z2-Z(B2+B-A)-AB=0
(10)
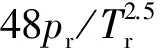
B=0.086 647pr/Tr
式中:pr——对比压力,pr=p/pc;pc——临界压力;Tr——对比温度,Tr=T/Tc;Tc——临界温度。
通过查找文献[5]中的物性数据表,可以获得流体的临界压力和临界温度。
文献[5]给出了Z的迭代解法,如下:
Zn=Zn-1-Fn-1/Fn-1′
2.3 莫里尔状态方程
莫里尔状态方程[5]如式(11) 所示:
c=0.000 461 1T/p-1.45/(T/100)3.1-
603 100p2/(T/100)13.5
(11)
式中:c——比容,c=1/ρ,m3/kg。
式(11)中压力为绝对压力,单位为MPa,文献[5]中也给出了该方法,但因采用的单位不同而与式(11)的系数稍有不同,该处不另行讨论。采用该密度计算方法,公式简单,准确度高,应用范围较广,尤其适合在控制系统组态中使用。
2.4 乌卡诺维奇状态方程
乌卡诺维奇状态方程[6]如式(12) 所示:
pv/RT=1+F1(T)p+F2(T)p2+F3(T)p3
(12)
F1(T)=(b0+b1φ+…+b5φ5)×10-9
F2(T)=(c0+c1φ+…+c8φ8)×10-16
F3(T)=(d0+d1φ+L+d8φ8)×10-23
φ=103/T
b0=-5.011 40,b1=19.665 7
b2=-20.913 7,b3=2.324 88
b4=2.673 76,b5=-1.623 02
c0=-29.133 164,c1=129.657 09
c2=-181.855 76,c3=0.704 026
c4=247.967 18,c5=-264.052 35
c6=117.607 24,c7=-21.276 671
c8=0.524 802 3
d0=-34.551 360,d1=230.696 22
d2=-657.218 85,d3=1 036.187 0
d4=-977.451 25,d5=555.889 40
d6=182.098 71,d7=30.554 171
d8=-1.991 713 4
该方法的计算量较大,但计算结果较准确,且适用范围广。结合式(12)与式(9),可以得出Z的另一种求解方法,如式(13):
Z=1+F1(T)p+F2(T)p2+F3(T)p3
(13)
2.5 高温高压流体状态方程
高温高压条件下的流体状态方程[6]如式(14) 所示:
ρ=18.56p/(0.01t-5.608×10-2p+1.66)
(14)
式中:t——温度,t=T-273.15,℃。
该方法只适用于1 MPa≤p<14.7 MPa且400 ℃≤t<500 ℃工况下的过热水蒸气。
2.6 中高温低压流体状态方程
中高温低压流体状态方程[6]如式(15) 所示:
ρ=19.44p/(0.01t-0.151p+2.162 7)
(15)
该方法只适用于0.6 MPa≤p<2 MPa且250 ℃≤t<400 ℃工况下的过热水蒸气。
2.7 分析对比计算结果
根据式(9)~式(15)的计算方法,将查表法所得密度值作为近似真值,比较其他密度计算方法的相对误差,同时根据式(10)和式(13)计算Z,结果见表1和表2所列。
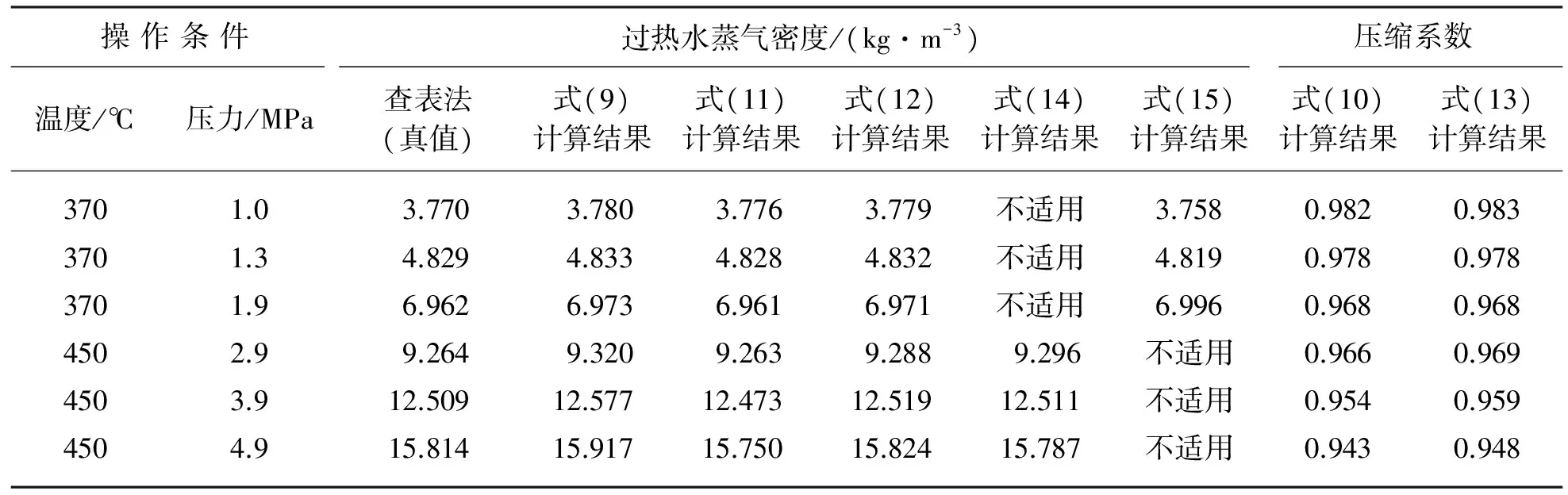
表1 过热水蒸气密度及压缩系数计算结果
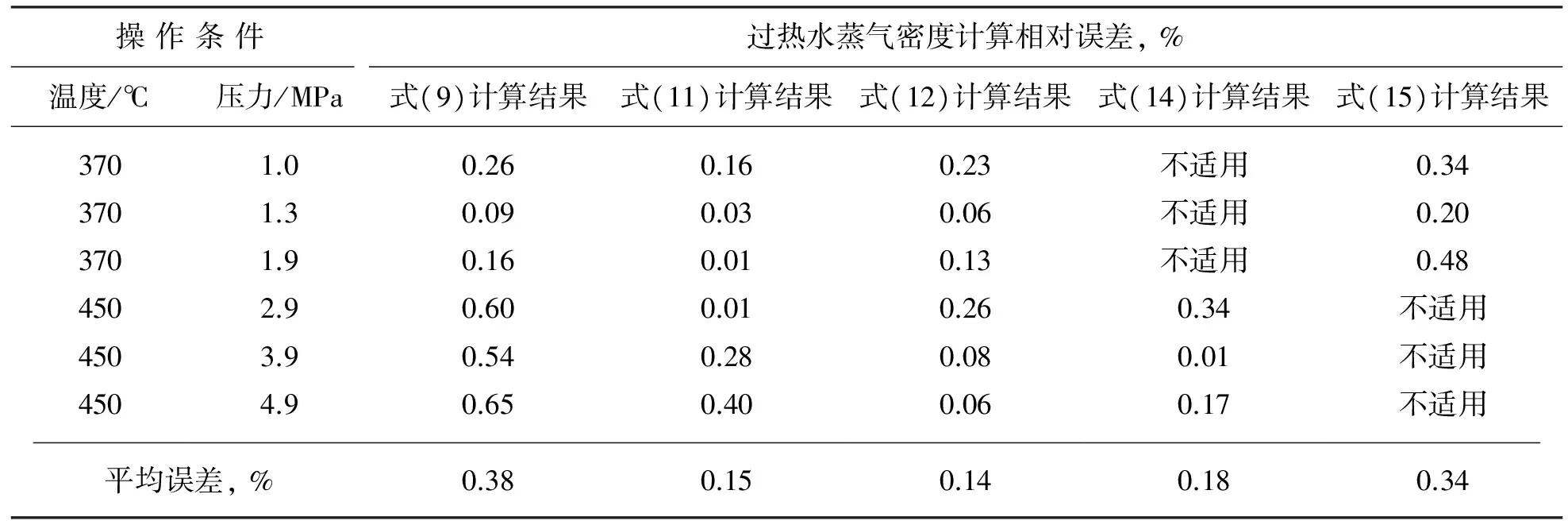
表2 过热水蒸气密度计算的相对误差
由表1和表2可知,有一定温度和压力范围限制的式(14)和式(15)的密度计算相对误差并没有低于密度通用计算公式(11)和(12)的计算结果,式(11)和(12)的密度计算结果更加接近真实值,相对误差较小,因此适用范围较广。式(9)的计算结果表明,在一定精度范围内,实际气体状态方程也可用于过热水蒸气。虽然式(10)和式(13)计算的气体压缩系数近似相等,但比较其对过热水蒸气密度的影响,可以推断出,式(13)的计算结果更加精确,推荐使用。
考虑到式(12)的计算公式比式(11)复杂,且计算相对误差近似相同,因此推荐将式(11)作为过热水蒸气密度的计算公式。将式(11)的计算结果ρ作为ρ补偿,代入式(5)、式(6)、式(7)中,即可得出过热水蒸气流量的温压补偿公式。例如,将式(11)与式(5)结合,可得出孔板、均速管流量计等差压式流量仪表用于测量过热水蒸气流量的温压补偿公式,如式(16)。
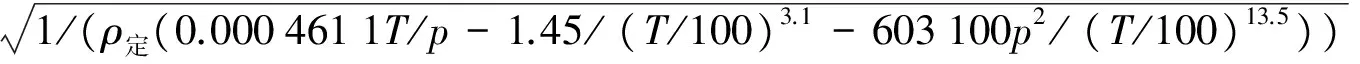
(16)
3 饱和水蒸气流量的温压补偿
3.1 查表法
理想饱和蒸汽的温度、压力和密度存在一一对应关系,通过查找饱和水蒸气的密度表,如文献[6]中的表5-20,可以获得一定温度或压力条件下的密度值。该法同样数据存储量大,仅适宜于手工查找。
3.2 实际气体状态方程
该方法与式(9)相同,此处不再赘述。
3.3 公式法
采用公式法[2]的计算公式如式(17)所示:
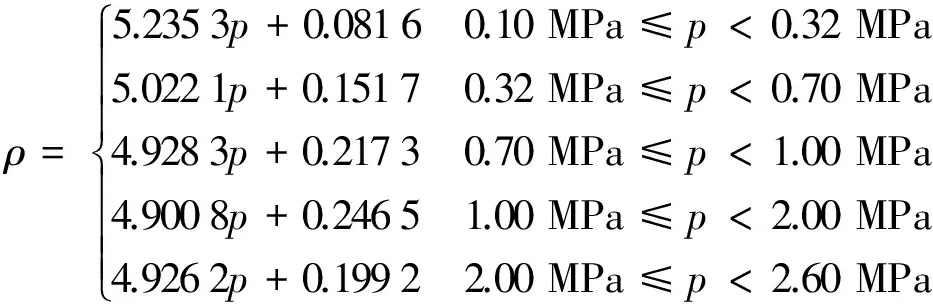
(17)
式(17)只适用于压力范围为0.1 MPa≤p<2.6 MPa的饱和水蒸气。
3.4 计算结果对比
根据式(17)和式(9)的计算方法,将查表法所得密度作为近似真值,比较其他计算方法的相对误差,结果见表3所列。
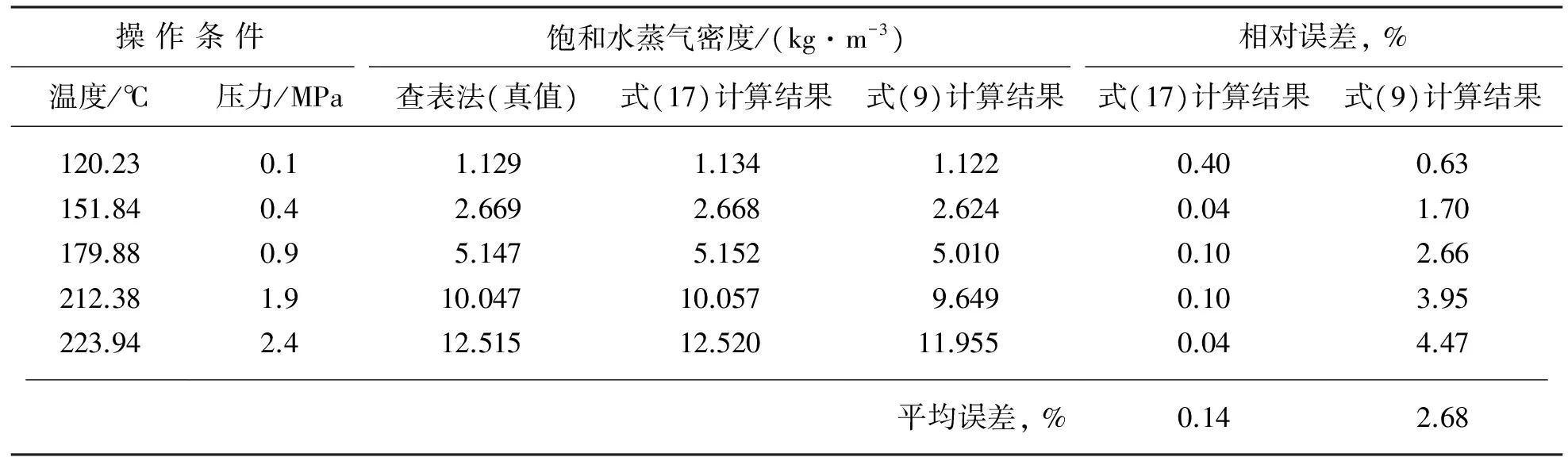
表3 饱和水蒸气密度计算结果对比
由表3可知,式(17)的计算精度保持在0.14%左右,而式(9)的计算结果有较大偏差,因此推荐将式(17)作为饱和水蒸气密度的计算公式。
将式(17)的计算结果ρ作为ρ补偿,代入式(5)、式(6)、式(7)中,即可得出饱和水蒸气流量的温压补偿公式。
4 结束语
通过对比分析水蒸气的几种密度计算方法,发现莫里尔状态方程更适合过热水蒸气的密度计算,分段函数式(17)更适合饱和水蒸气的密度计算,乌卡诺维奇状态方程更适合过热水蒸气的压缩系数计算,实际气体状态方程适用于过热水蒸气。最后,本文给出了水蒸气流量的温压补偿计算公式。
[1] 王雪梅,张悦崑,安铁夫,等.HG 20507—2014自动化仪表选型设计规范[S].北京:化学工业出版社,2014.
[2] 许秀.测控仪表及装置[M].北京:中国石化出版社,2012:118-149.
[3] 瓦格纳 W, 克鲁泽 A.水和蒸汽的性质[M].北京:科学出版社,2003.
[4] Wagner W.Thermodynamic Properties of Water and Steam[J].IAPWS Industrial Formation,1997(09):11-13.
[5] 陆德民,张振基,黄步余.石油化工自动控制设计手册[M].3版.北京:化学工业出版社,2000.
[6] 王森,纪纲.仪表常用数据手册[M].2版.北京:化学工业出版社,2012:173- 176.
[7] 崔配配,贾清泉, 刘博,等.M型流量计的数值模拟与数字化标定[J].化工自动化及仪表,2015,42 (09):980-983,1059.
[8] 谢政,潘茂强.德尔塔巴流量计的流量计算与误差补偿[J].化工自动化及仪表,2015,42 (07):746-748,752.
[9] 吴晨.浅析蒸汽流量计量中温度、压力补偿的数学模型[J].计量与测试技术,2008, 35(09):32-38.
[10] 闫娜.浅谈差压式流量计的温压补偿计算[J].石油化工自动化,2016,52(04):17-19.
TemperatureandPressureCompensationCalculationonSteamFlowMeasurement
Liu Cuifeng, Zhang Yuwei, Kong Xiangcui
(Xinjiang Branch, China Huanqiu Contracting & Engineering Corporation, Karamay, 836699, China)
s:Two measuring methods and principle of temperature and pressure compensation of steam flow are introduced.By studying calculation methods of steam density, and comparing and analyzing calculation error, one recommendable calculation method of steam density is proposed.Computational formula for temperature and pressure compensation for steam flow measurement is obtained.Two kinds of calculation method of compressibility of superheated steam are studied at the same time.A recommendable calculation method is given with the calculation programs compiled with Matlab.Whether actual gas state equation could be applied to steam is discussed.
superheated steam;saturated steam;temperature and pressure compensation;density;compressibility coefficient
稿件收到日期:2017-07-24,修改稿收到日期2017-09-11。
刘翠凤(1971—),女,湖南常德人,1996年毕业于大庆石油学院,获学士学位,现就职于中国寰球工程公司新疆分公司,从事自控工程设计与管理工作,任高级工程师。
TH814
B
1007-7324(2017)06-0017-04

