基于Eigen和OpenCV的图像算法加速

舒 畅，秦肖臻

(华中科技大学 自动化学院，湖北 武汉 430074)

基于Eigen和OpenCV的图像算法加速

舒 畅，秦肖臻

(华中科技大学 自动化学院，湖北 武汉430074)

OpenCV作为一款免费、开源的计算机视觉库已广泛应用于图像处理的各种项目开发中。在算法实现中，高性能的线性代数运算库能提升算法的执行效率和算法实现灵活性。介绍了Eigen线性代数运算库，并在矩阵运算效率上与OpenCV进行了比较。以基于SVD分解的图像压缩算法为例，将Eigen和OpenCV进行联合编程并给出了主要代码。

OpenCV；Eigen；图像处理；算法加速

0 引言

在数字图像处理中，先将图像传感器获取的数据进行采样和量化。处理后的图像数据可以等价为一个实数矩阵，该矩阵中的每个元素称为像素[1]。因此向量和矩阵等线性代数运算成为数字图像处理的基本和必备工具。

OpenCV[2]封装了部分常用的线性代数运算操作，比如矩阵相乘、求逆、矩阵奇异值分解(SVD)以及解线性方程组等。这些数学操作是大部分图像处理算法的基本构成单元，对其进行软件优化和硬件加速[3]可以很大程度上缩短图像处理算法的运行时间，提升算法的实时性。将OpenCV与Eigen进行联合编程可以很大程度突破大型矩阵运算时的速度瓶颈。

1 Eigen库介绍

1.1 Eigen简介

Eigen[4]是基于C++模板技术、为线性代数计算进行高度优化的开源库。著名深度学习框架TensorFlow[5]中的许多核心算法实现也借助[6]于Eigen库。Eigen具有如下特点。

(1)与OpenCV相比，Eigen原生支持复数型矩阵和动态维度矩阵，给算法实现带来了很大的便利和灵活性。

(2)除了运算上的优化和通过C++模板技术支持惰性求值(Lazy Evaluation)，同时还可以对SSE 2/3/4，ARM NEON等指令集进行专门的向量化(Vectorization)编译加速。

1.2 基于Eigen库的开发

除了C++标准库外，Eigen不依赖于任何第三方包而且使用简便。以Microsoft Visual Studio Community 2015为例，将Eigen头文件所在路径添加到项目的引用目录便可完成开发环境的配置。

2 OpenCV与Eigen矩阵运算性能比较

2.1 矩阵运算性能测试环境

性能测试平台的主要硬件参数包括型号为Intel i7-4790K(主频4 GHz)的处理器、容量为8.0 GB的内存。软件测试环境为Windows 64位系统以及Microsoft Visual Studio Community 2015。随着版本升级，开源软件的性能也会有很大提升。测试时均选取当前代码库的最新版本，即OpenCV3.2.0以及Eigen3.3.3。

性能测试中选取了矩阵求逆、SVD矩阵分解两项计算量大且较常用的矩阵运算，分别以浮点型和双精度方式运算。矩阵维度主要包括50×50、100×100、200×200、500×500、1 000×1 000共5类。为了消除数据大小对不同维度矩阵计算的影响，先用随机数同时填充在OpenCV和Eigen中维度为1 000×1 000的矩阵，再将1 000×1 000型矩阵分块为其他小尺寸矩阵。为了接近真实编程场景，矩阵运算后会将结果赋值给新的变量，而不是单纯计算矩阵函数所需时间。其中随机数的范围取为[-10,100]。以双精度、大小为20×20和1 000×1 000的矩阵和SVD分解为例，性能测试的主要函数代码如下：

void createMatd(Mat &mat,MatrixXd &emat,int dim)

{

random_device rd;

//声明随机数生成器

double* p = NULL;

//指向OpenCV图像矩阵的行指针

double temp;

for (int i = 0; i < dim; i++)

{

p=mat.ptr(i);

for (int j = 0; j < dim; j++)

{

uniform_real_distribution dist(-10,100);

temp = dist(rd);

//如果是单精度或者双精度保留三位小数

temp = (int)(temp * 1000 + 0.5);

temp = (double)(temp / 1000);

emat(i,j) = temp;

p[j] = temp;

}

}

}

//OpenCV矩阵SVD分解测试函数

void cvSVDOperation(Mat testMat)

{

clock_t tCount = clock();

for (int count = 0; count < 100; count++)

{

SVD tempMat(testMat,SVD::FULL_UV);

Mat U=tempMat.u;

Mat W=tempMat.w;

}

printf("Time taken: %.10f s ",(double)(clock() -tCount) / CLOCKS_PER_SEC / 100);

}

//Eigen矩阵SVD分解测试函数

template

void eigenSVDOperation(T testeigenMat)

{

clock_t tCount = clock();

for (int count = 0; count < 100; count++)

{

BDCSVD svd(testeigenMat,ComputeFullV | ComputeFullU);

T U = svd.matrixU();

T V = svd.matrixV();

}

printf("Time taken: %.10f s ",(double)(clock() -tCount) / CLOCKS_PER_SEC / 100);

}

2.2 矩阵运算性能测试结果及分析

运行矩阵运算性能测试程序，分别记录在不同矩阵运算精度和矩阵大小下的运行时间，进行整理后如表1～4所示。从表中可以看出：

(1)从元素数值类型的角度而言，在OpenCV中随着矩阵维数增加，浮点型运算的效率较双精度运算效率提升较小；相反Eigen对于大矩阵，浮点型运算比双精度要快两倍左右。

(2)从开发库的角度比较，对于类似20×20的小矩阵，Eigen略显逊色。而随着矩阵维度的增加，优势越来越明显。对于1 000×1 000的矩阵，在浮点型矩阵求逆运算上比OpenCV快6.09倍；在双精度矩阵求逆运算上比OpenCV快18.02倍。

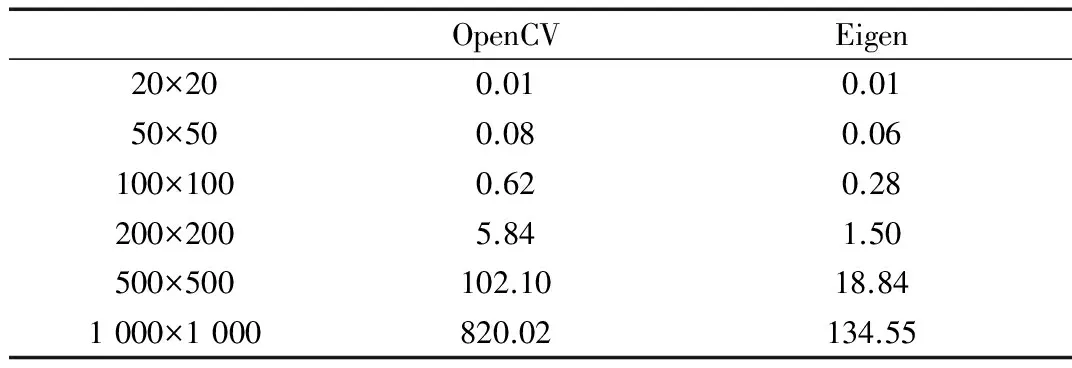
表1 浮点型矩阵求逆运算对比 (ms)

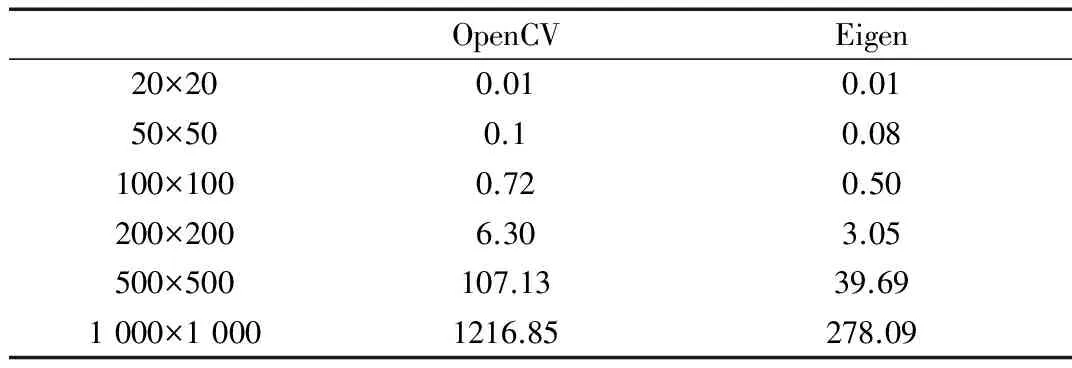
表2 双精度矩阵求逆运算对比 (ms)

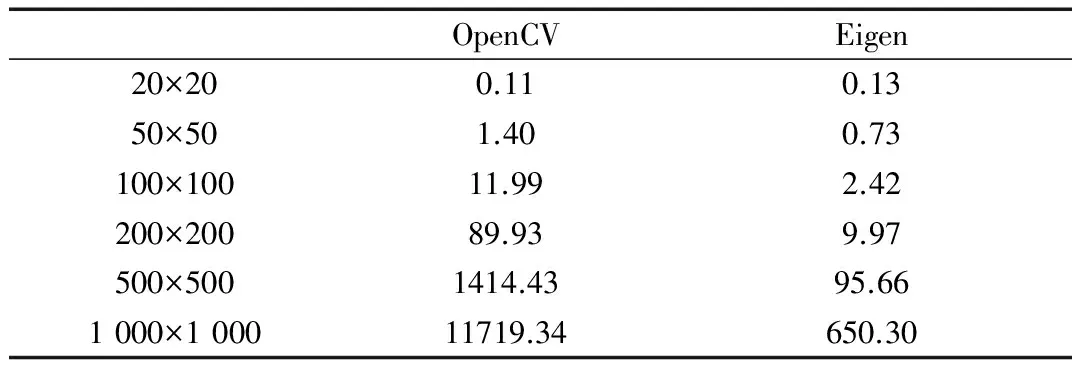
表3 浮点型矩阵SVD分解对比 (ms)

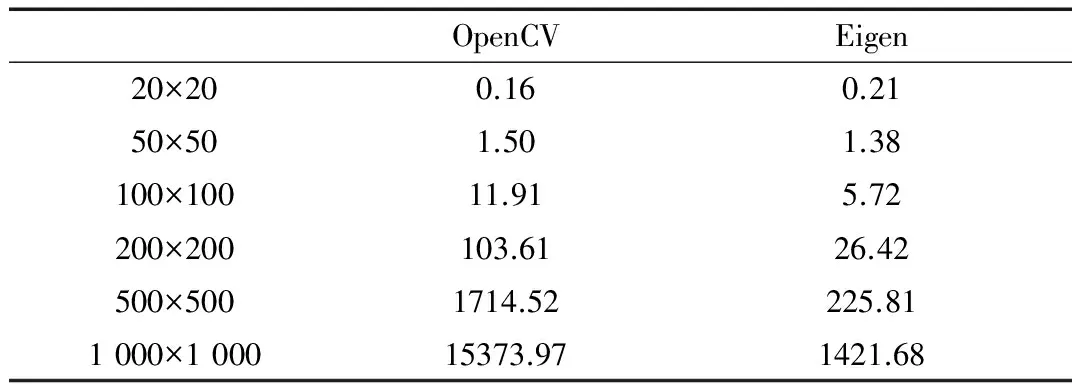
表4 双精度矩阵SVD分解对比 (ms)

3 基于Eigen、OpenCV联合编程的图像压缩算法

3.1 SVD矩阵分解介绍

SVD分解在实数范围内，将一个秩为r的矩阵Am*n分解为如下形式：

A=UΣVH

(1)

其中U是m×m的正交矩阵，V是n×n的正交矩阵，分块矩阵Σ的形式如下：

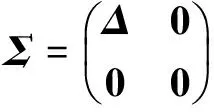
(2)

其中Δ是秩为r的对角矩阵，Δ对角线上的元素称为奇异值。设矩阵A的奇异值为σ1>=σ2>=…>=σr>0，ui、vi对应矩阵U、V的第i列，则矩阵A的奇异值展开式如下：

A=σ1u1v1+σ2u2v2+…+σrurvr

(3)

3.2 Eigen和OpenCV联合编程

在Eigen中，矩阵数据默认按列优先进行存储；在OpenCV中，矩阵数据按行优先进行存储。Eigen和OpenCV联合编程时，需要对它们进行转换，OpenCV矩阵转Eigen矩阵的代码如下：

Matimg;

//转换为Eigen中的矩阵

Eigen::Map> eigenMat(image.ptr(),image.rows,image.cols);

在上述转换过程中，主要是对内存中数据的复用，并没有大量耗时的数据复制等操作，几乎不占用额外时间。

Eigen矩阵转OpenCV矩阵可以调用函数eigen2cv,函数的第一个参数为待转换的Eigen矩阵，第二个参数是OpenCV目标矩阵。对于1 000×1 000的双精度矩阵，100次转换时间均值为2～3 ms。对于大矩阵SVD分解而言，这个转换时间在可接受范围内。

3.3 基于SVD矩阵分解的图像压缩算法

在公式(3)中，较大的奇异值所对应的项包含更多的图像信息，只取矩阵A中部分较大的奇异值，相对于m×n的存储量，只需r×(m+n+1)的存储空间。r越小，图片压缩率越大，但图片也会逐渐变得模糊。

这里选取的测试图片分辨率为500×500，SVD分解后的奇异值个数为498，选取位于前20、50、100较大的奇异值来重构原矩阵。以位于前20的奇异值重构原矩阵为例，主要代码如下：

Matimg = imread("lenna.png");

//读取图片

cvtColor(img,img,CV_BGR2GRAY);

//转化为灰度图像

img.convertTo(img,CV_64FC1);

//转化为双精度矩阵

int m = img.rows;

//得到图像行、列值

int n = img.cols;

//将OpenCV中的矩阵转化为Eigen中矩阵

Eigen::Map>

eMat(img.ptr(),m,n);

//在Eigen中进行SVD分解

BDCSVD svd(eMat,ComputeFullV | ComputeFullU);

MatrixXd U = svd.matrixU();

MatrixXd V = svd.matrixV();

MatrixXd S = svd.singularValues();

//通过奇异值构造分块矩阵Σ

MatrixXd diag(m,n);

diag.setZero();

//取前100个奇异值填充分块矩阵Σ对角线

for (int i = 0; i < 100; i++)

diag(i,i) = S(i,0);

V.transposeInPlace()

MatrixXd recImg = U*diag*V;

MatcvMat = Mat::zeros(recImg.rows(),recImg.cols(),CV_64FC1);

eigen2cv(recImg,cvMat);

cvMat.convertTo(cvMat,CV_8UC1);

imwrite("100.png",cvMat);

原图和重构图像如图1～4所示。

图1 前20个奇异值

图2 前50个奇异值

图3 前100个奇异值

图4 原图

可以发现，图3基本保留了原图的大部分细节，在不放大图像的情况下与原图几乎毫无差异，同时达到了约2.5倍的压缩比。

4 结论

基于Eigen线性代数库加速的OpenCV图像处理程序在实际运行速度上有明显的提升，同时Eigen更加丰富的矩阵运算操作也给算法实现带来了很大的便利。随着新的图像处理算法不断提出，Eigen也将越来越广泛地应用到算法的具体实现中。本文中OpenCV和Eigen联合编程的方法对于其他需要加速的图像算法具有较高的参考价值。

[1] GONZALEZ R C,WOODS R E. 数字图像处理[M].阮秋琦,阮宇智,译.3版.北京:电子工业出版社,2011.

[2] OpenCV. Introduction[EB/OL].(2016-12-23)[2017-06-30]https://docs.opencv.org/3.2.0/d1/dfb/intro.html.

[3] 张俊涛，王园伟，庞多.一种硬件加速OpenCV的图像处理方法研究[J].微型机与应用，2015，34(22)：41-43.

[4] JACOBB B,GUENNEBAUD G. Eigen is a C++ template library for linear algebra: matrices,vectors,numerical solvers,and related algorithms[EB/OL].[2017-06-30]http://eigen.tuxfamily.org/index.php?title=Main_Page.

[5] Google. Getting started with TensorFlow[EB/OL].[2017-06-30]https://www.tensorflow.org/get_started/get_started.

[6] ABADI M,AGARWAL A,BARHAM P,et al. Tensorflow: large-scale machine leaning on heterogeneous distributed system[J/OL].(2016-03-14)[2017-06-30]https://arxiv.org/abs/1603.04467.

Image algorithm acceleration based on Eigen and OpenCV

Shu Chang,Qin Xiaozhen

(School of Automation,Huazhong University of Science and Technology,Wuhan 430074,China)

As a free and open-source computer vision library,OpenCV has been widely used in image processing of various project development. During the algorithm implementation,the high performance linear algebraic library can improve the efficiency of the algorithm and the flexibility of the algorithm implementation. This paper introduces the linear algebraic computation library Eigen and compares it with OpenCV in matrix operation efficiency. Taking the image compression algorithm based on SVD decomposition as an example,Eigen and OpenCV are jointly programmed and the main code is given.

OpenCV; Eigen; image processing; algorithm acceleration

TP391

A

10.19358/j.issn.1674-7720.2017.24.012

舒畅，秦肖臻.基于Eigen和OpenCV的图像算法加速J.微型机与应用，2017,36(24)：40-43.

2017-06-30)

舒畅(1993-)，男，硕士研究生，主要研究方向：图像算法。

秦肖臻(1965-)，女，副教授，主要研究方向：计算机集成与信号处理。