巧构几何图形 妙解代数问题

李冰冰

数学是中学的一门重要学科，而数学中的代数是比较复杂且枯燥的，如何解决代数问题，是数学学习过程中的一个难点，因此在解题过程中需要寻找不同的思路与方法。本文主要探讨如何通过构造几何图形解决代数问题，将数与形结合起来，把代数问题转换成几何图形，有利于直观地看出代数式所表达的内容，能够通过图形将复杂的代数问题简单化，提高解题效率，开发学生思维灵活性，提高学生分析问题、解决问题的能力。

一、代数问题几何化的必要性

将代数问题几何化这一思路方法，本质上就是把抽象的代数问题和具象化的几何问题相互结合起来，相互弥补不足之处，如几何问题的长处是能够直观地看出图形，能直观地理解两者之间的关系，但是不足之处则是表达不够简练。而代数式的表达都比较简练，但是代数是公式化的问题，解决起来比较复杂，没有直观的形象，因此代数问题是让很多学生都头痛的问题。将代数问题几何化其本质就是把抽象问题具体化，把复杂问题简单化，通过对图形的处理，能够发挥出直观图对抽象代数的支柱作用。

目前全国正在大力推行素质教育，而创新教育是素质教育的重要环节，因此，培养学生的创新能力是全国推广素质教育的重点，而创新能力培养的重点就是加强学生的创新思维能力，创新思维能力的实质是通过不同的思路、不同解题方法的综合运用，在前人解决问题的基础上，通过发散性思维的创造，能够有新的解决问题的思路，在数学的学习上培养学生的创新能力，也显得尤为重要。

本文通过对勾股定理将代数问题几何化的研究，开拓初中生的思维能力，培养解决问题的创新方法。

二、代数问题几何化的基本步骤

数学是一门很神奇的学科，数学中的很多代数问题都可以转换成图形来解决，如果单纯使用代数来解决问题，则会比较困难，而数学中的数字都能转换成图形，这就代表在代数解题时也可以通过构建图形来解决。一些代数问题本身比较复杂，对于初中生来说解决起来比较困难，甚至会出现无从下手的情况。通过将有明显意义的代数转换成几何问题来研究，从而获得问题的解决方法，这一方式通常被称为构造图形法。但是代数问题几何化的关键，在于引导学生去观察代数、分析代数的性质，将代数类比成几何图形，发挥联想的能力，然后找出代数和几何的共同点，建立几何模型。一般用几何方法来解决代数问题，都是以下几个步骤：首先，需要构建一个代数模型，将需要求解或推导的代数通过适当的变形和转换，使其能够成为我们应用公式的图形；其次，通过第一个步骤的变形，建立一个几何模型，注意，这个几何模型需要符合代数式的特点，例如，面积是平方，体积是立方，两点之间距离是线段，像三角形、圆形、椭圆、圆柱等，都可以用来构建几何模型；最后，将代数问题几何化，就是在第二步建立几何模型的基础上，通过分析几何模型，其实就是分析代数式的过程，解决代数式中需要推导的问题。

三、代数问题几何化的应用

勾股定理是在一个直角三角形中直角边分别为a和b，斜边为c，直角边a的平方加b的平方等于c的平方。勾股定理的证明方法多种多样，而它是在数学定理中能够被证明最多的定理之一。所以勾股定理可以说是数形结合的典范，无论是通过图形来推导勾股定理，还是用勾股定理来构建图形，都是能够通过很多方法去验证的。

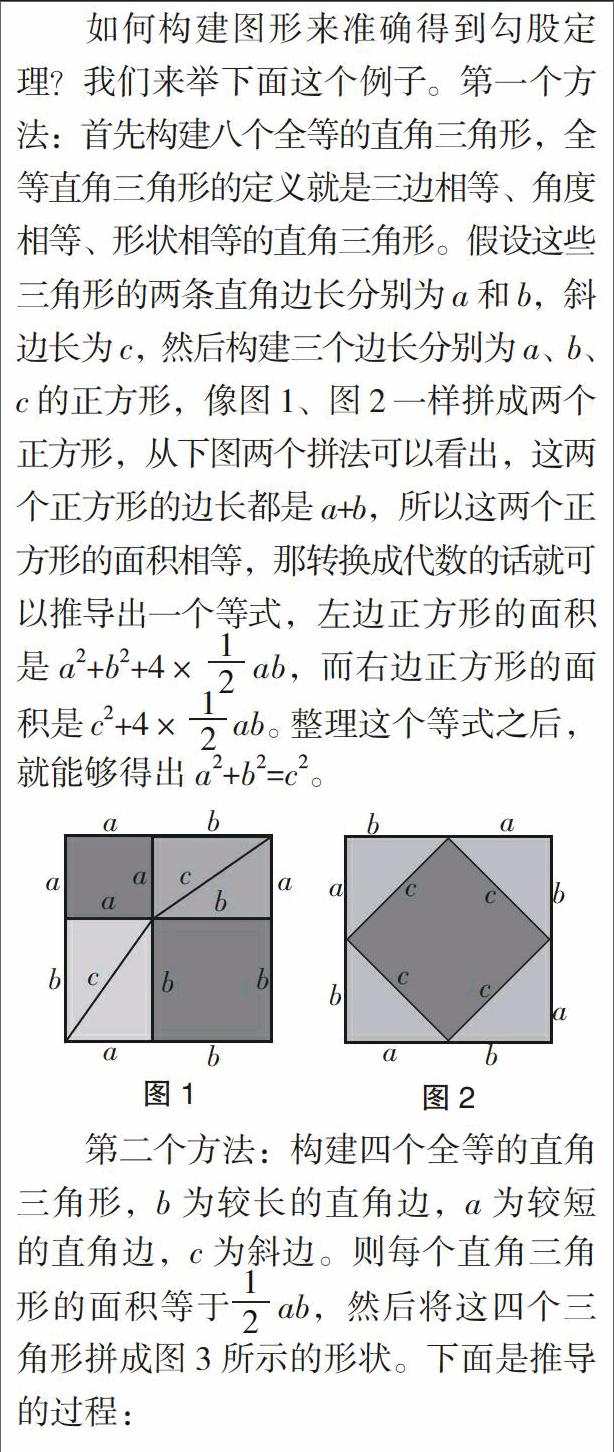
如何构建图形来准确得到勾股定理？我们来举下面这个例子。第一个方法：首先构建八个全等的直角三角形，全等直角三角形的定义就是三边相等、角度相等、形状相等的直角三角形。假设这些三角形的两条直角边长分别为a和b，斜边长为c，然后构建三个边长分别为a、b、c的正方形，像图1、图2一样拼成两个正方形，从下图两个拼法可以看出，这两个正方形的边长都是a+b，所以这两个正方形的面积相等，那转换成代数的话就可以推导出一个等式，左边正方形的面积是a2+b2+4×ab，而右边正方形的面积是c2+4×ab。整理这个等式之后，就能够得出a2+b2=c2。

其实，勾股定理的证明方法有很多种，勾股定理可以说是所有数形结合的基础，也是最早开创数形结合的鼻祖。国内外研究勾股定理的学者专家数不胜数，这里只是简单列举一些比较基本的方法，也是为今后数形结合的学习打下基础。

总之，数学问题的解决方式很多都是相通的，尤其是代数与图形之间。代数在数学中是一个很宽泛的概念，因此我们在解决代数问题时，不能仅把思路局限于代数之中，更多时候可以换一种解题思路，将代数转换成几何图形，这是一种很好的方法。在一定程度上将代数问题转换成几何图形的问题，有利于直观地看出代数式所表达的内容，也能够通过图形将复杂的代数问题简单化，提供多种解题思路。在这转化过程中，锻炼了学生的推导能力。将代数问题转换成几何問题对学生能力也是一种考验，如何将代数和几何的图形应用联系起来，需要学生充分发挥发散性思维，由此锻炼了学生的动脑积极性和思维灵活性。另外，将数与形结合起来，有利于将复杂的问题简单化，提高解题效率，数和形的结合，能够加强学生对数学的综合学习能力，也可以提高学生分析问题、解决问题的能力。

（作者单位：福建省漳州市石亭中学）