小学数学分数应用题教学方法探析

黄菊昌

【摘要】本文论述分数应用题教学应降低学习难度、提高教学效率，提出了五种教学途径：根据题意创设应用题教学情境，找准关键词确定标准单位，提高学生画分数线段图的能力，利用列式的方法解答，追求分数应用题解答的完善性。

【关键词】小学数学 分数应用题 教学方法

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2017）10A-0087-02

分数应用题是小学数学教学中的一项重点内容，也是学生在学习过程中普遍反映的难点问题。在小学阶段，学生在解答较为复杂的分数乘除法应用题时会存在一定的困难，特别是在传统的教学观念下，学生处于被动地位，知识还没理解透彻就要面对大量的习题，导致做题时常常出现错误。笔者认为，在解答分数应用题时，教师要引导学生准确把握题目中的关键词，通过关键词来确定标准单位，然后再利用分数线段图来降低解题难度，最后通过列式解答。这样教学，能进一步提高学生的做题效率。

一、根据题意创设应用题教学情境

在大多数小学分数应用题中，虽然存在较为复杂和抽象的数量关系，但其中大多数题目的情节往往是和学生的日常生活接近的。在应用题的教学过程中，教师可以根据题意，结合实际的教学情况创设类似的教学情境，促进学生理解题目中的数量关系，从而降低分数应用题的解题难度。例如，小亮的身高比小红高[18]，已知小红身高123cm，那么小亮的身高是多少？在解答这道题时，教师就可以结合学生的实际情况创设类似的教学情境。首先教师在班级中挑选出符合条件的学生，然后让学生仔细观察，通过比较身边同学的身高来理解题意，知道是“谁比谁高[18]”，从而明确“谁是谁的[18]”这样的数量关系。通过观察和比较，学生很快就会明白小亮的身高是小红的身高再加上小红身高的[18]，或者也可以理解为小亮的身高是小红身高的1[18]倍。

创设日常生活情境对思维能力较低的学生解答分数应用题是很有帮助的，它既能够降低题目的难度，又可以激发学生学习的积极性，进而找出题中的数量关系，达到快速、准确解答的目的。

二、找出关键词，确定标准单位

小学分数应用题是学生必须掌握的数学知识，如何提高分数应用题的教学效率是众多小学数学教师正在探索的课题。笔者认为，要提高学生解答分数应用题的正确率，就应该采取科学有效的教学策略，找准题目的关键词，确定标准单位，进一步锻炼学生的数学思维能力和分析能力，避免一味地让学生死记硬背公式、套用模式的教学行为。

在小学数学教学中，应用题相较于其他数学题目，它的信息含量无疑是比较多的，为了让学生准确地解答这类题目，笔者认为，训练学生找准关键词，确定标准单位是学生在读题过程中必须完成的任务。学生在解答分数应用题时，首先要准确地找出题目中的关键词，厘清其中的数量关系，从而确定题目要求使用的单位是什么。要想确定题目中的标准单位，就必须教会学生寻找题目中的关键语句。一般来说，分数应用题中含有分数的部分都是关键语句（所谓关键语句，就是指在应用题中涉及分数的表达语句，其形式一般为：A是B的几分之几，或者B的几分之几是A等）。例如，小明的橘子是小亮的1[12]倍，小强的橘子是小明的[23]，小明有6个橘子，那么小亮和小强各有几个橘子？在这道分数应用题中，教师首先要让学生明确其中的关键语句，即“小明的橘子是小亮的1[12]倍，小强的橘子是小明的[23]”。找好关键语句之后下一步就要明确题目中的标准单位，教师应该明确地告知学生，题目中所使用的标准单位就是在两个关键语句的两个量中，应该使用哪个量作为标准，那么那个量就是分数应用题中的标准单位。例如，本题中我们是以小明的橘子“1”来做衡量标准的，因此本题的标准单位为“1”。学生根据这种方法再通过反复练习，就能够真正抓住题目中的关键点，进而解答问题。让学生明确分数应用题中的标准单位“1”，可以有效地避免学生仅仅根据一些关键词就理所当然地按照固有逻辑来进行判断，如果题目中涉及两个以上的单位，那么学生还需要学会进行分率的转化。

三、提高学生画分数线段图的能力

在小学数学教学中，分数应用题中所涉及的数量关系相比较其他题型而言是较为复杂的，为了让学生在解题过程中有一个更加明确的思路，教会学生画线段图就是一个有效的方法。在学生解答分数应用题的过程中，利用线段图可以帮助学生将部分和整体的数量关系都表示出来，使学生能够直观地理解其中蕴含的数量关系，有利于学生厘清解答分数应用题的具体思路。因此，学会画分数线段图是学生解决分数应用题的一个重要手段，有利于学生的解题思维与分析线段图同步进行，提高做题效率。教师在小学数学教学过程中既要锻炼学生分析线段图的能力，同时也要培养学生根据题意动手画图的能力，只有从两个方面同时着手，才能够真正提高学生的数学思维能力。根据多年的教学经验，笔者认为教师在指导学生画线段图时需要注意以下几点：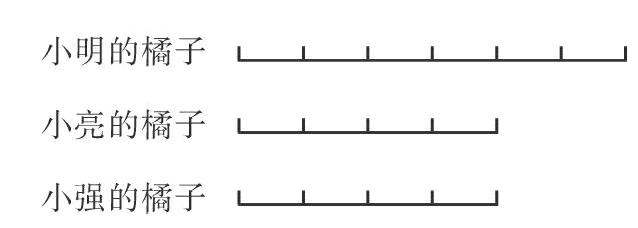

首先，画线段图要讲究由简入繁，循序渐进，切忌急功近利。学生在做数量关系较为简单的分数应用题时，教师应强调学生借助画线段图来分析，学会分析线段图中的数量关系，逐步上升为亲手绘制线段图。

其次，在学生掌握好基本的画线段图的方法之后，教师还应培养学生灵活地使用线段图来解决数学难题的能力。例如，上例中在求橘子的问题上，如果我们从小亮拥有的橘子着手开始画线段图，那么要想得出小强的橘子个数，就势必要费一番周折；但如果我们从与他们两人都有关系的小明开始入手画线段图，则很容易就可以计算出小亮和小强所拥有的橘子个数。由此可以看出，學生只学会画线段图还不行，还要学会将其灵活地运用到具体的数学问题中，这样才是正确解答分数应用题的可取之道。如图所示：