基于随机时变路网的运输路径选择*

刘 帅，唐伯明，刘 松

(1.重庆交通大学 土木工程学院，重庆 400074； 2.重庆交通大学 交通运输学院，重庆 400074)

基于随机时变路网的运输路径选择*

刘 帅1，唐伯明1，刘 松2

(1.重庆交通大学 土木工程学院，重庆 400074； 2.重庆交通大学 交通运输学院，重庆 400074)

针对运输路网中各路段上的行驶时间受交通管理、交通拥挤、天气变化等不确定性因素的影响而呈现出随机时变的特点，引入了路网评审技术中的三时估值法，建立了随机时变路网下以行驶时间最短为目标的路径优化模型，提出了车辆跨时段行驶时路段的时间依赖函数，设计了动态规划标号算法求解。算例求解优化结果的对比分析验证了模型及算法的有效性。

交通运输工程；随机时变；跨时段；动态规划

0 引 言

交通拥挤、交通事故等因素的不确定性，导致车辆在各路段行驶中的行驶成本、行驶时间等也具有不确定性，呈现出随机时变特性。随机时变路网模型由于考虑了现实路网的时变性与随机性，能更好的反映实际交通路网状态，其中如何合理的处理具有时变性和随机性的路段权值是关键问题。

董振宁等[1]考虑了路段权值的随机性，假设路段权值服从指数分布，以期望路长最短为目标对随机路网最短路进行优化；范巍巍等[2]、郑龙等[3]、周光发等[4]研究了带约束条件的随机路网最短路问题。但以上学者没有考虑路段权值随时间不同而呈现出的时变特点。贺政纲等[5]考虑了路段权值的时变特点，对行驶风险随时间变化的带时间窗的最短路进行优化；范文璟等[6]、刘丽萍等[7]考虑了在时变路网中带约束条件的应急救援路径优化；彭勇等[8]对时变路网中以配送完成时间最早为优化目标的车辆配送路径优化进行了研究；王莺等[9]研究了时变路网中，以运输成本和运输损耗为目标的最短路问题。这些学者考虑了路段权值的时变性，但没有考虑路段的随机性。

将路网的随机性和时变性特点同时加以考虑的学者不多，陈京荣等[10]考虑了路网的随机性和时变性特点研究最短路问题；魏航等[11]考虑了路网的随机时变特点对有时间窗限制的应急路径进行优化；曹慧等[12]利用鲁棒优化方法研究了随机时变路网下的最短路径问题。虽然以上学者同时考虑了路网的随机性和时变性，但是没有考虑随机时变网络中不可忽略的first input first output(FIFO)问题以及跨时段行驶问题。

笔者运用计划评审技术中解决非确定型统筹问题所采用的三时估计法来处理随机时变路网路段权值问题。三时估计法是实际工程中估计工作持续时间的主要方法之一，是一种有效的工程项目进度风险分析方法。车辆在道路上的行驶时间可认为是车辆在道路上需要工作的时间，与工程项目工序完成时间一致，所以，三时估计法也可用于运输中的不确定性分析。笔者借鉴三时估计法和动态规划标号法，寻求在随机时变路网环境下，车辆从起点O到终点D，以行驶时间最短为目标，满足FIFO规则和车辆跨时段行驶的最短路线。

1 问题描述及条件假设

1.1 问题描述

1.2 条件假设

1) 各路段的交通状况相互独立。

3) 车辆在各节点处的等待时间为0。

2 问题建模

2.1 随机时变路网下行程时间分析

路段的行程时间由于受交通事故、天气变化等因素影响难以准确估计而呈现出随机时变特性，因此，笔者引入计划评审技术中解决非确定型问题所采用的三时估计法来处理路段行程时间随机时变的不确定性问题，把随机时变路网转化为确定性时变路网。将路段的时间分为悲观时间、乐观时间，及在正常情况下的最可能时间，再计算其期望时间和方差。

(1)

(2)

在随机时变路网中，路段的权值与出发时间有关，因此，确定路网的时间依赖函数就非常重要。当前，关于随机时变路网中的时间依赖函数的研究大多还处于较为理想的状态。MALANDRAKI C等[13]首次采用时间分段函数作为时间依赖函数来表示路段行程时间，如图1。

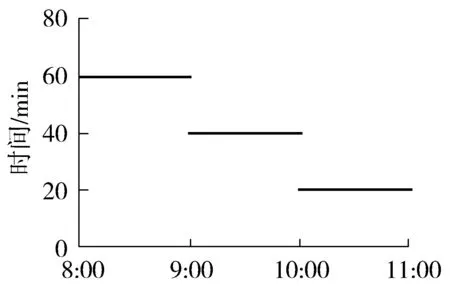
图1 行驶时间时间依赖函数Fig.1 Time-dependent function of travel time

图1显示路段(i，j) 在不同时段所需的行驶时间，如果1号车在 08：50 离开i，在09：50到达j；同时，2号车在09：00 离开i，却在09：40到达j，比1号车早到，违反了FIFO原则。因此尽管时间分段法分段数越多越接近实际情况，但是该方法为了满足路网的先入先出FIFO特性，需要假定车辆在节点处等待一定时间，这与实际情况不符。

K. SUNG等[14]证明了使用如图2的行驶速度时间依赖模型满足FIFO原则。

图2 行驶速度时间依赖函数Fig.2 Time-dependent function of travel speed

为了使得车辆在随机时变路网中的行驶时间满足FIFO原则，笔者设计了以下方法计算路段(i，j)的行驶时间。

同理可得，车辆由节点i出发到达节点j所需跨越时段数N。

1) 如果车辆完全在k时段内行驶完路段(i，j)，即N= 0，不跨时段行驶，由于假设在各个节点处等待时间为0，故节点的到达时间等于出发时间。则抵达节点j的时刻Tj为

(3)

2) 若车辆在路段(i，j)上行驶由k时段跨越到了k+1 时段，即N= 1，则到达j的时刻Tj为

(4)

命题若车辆在路段(i，j)上行驶从k时段跨越到了k+N(N≥2 )个时段，则到达j的时刻Tj为

(5)

推导

1)当车辆从k时段跨越到了k+2个时段时，到达节点j的时刻Tj为

2)当车辆从k时段跨越到了k+3个时段时，到达节点j的时刻Tj为

3)当车辆从k时段跨越到了k+N个时段时，到达节点j的时刻Tj为

2.2 数学模型

设X是路径可行解的集合，λ(λ∈X)是起点O和终点D之间的一条可行路径，则所求问题的优化模型为

(6)

约束条件如式(7)～式(9)：

(7)

(8)

(9)

3 算法设计

由于考虑了路网的随机性和时变性，随机时变路网路径求解算法比静态路网复杂。随机时变网络已被证明是NP完全问题(non-deterministic polynomial complete problem)。笔者将其转化为满足FIFO 特性的确定型时变路网问题，可设计动态规划和标号法求解。对于一个随机时变的运输网络，在求解过程中，通常可将其划分为若干个阶段，然后逐个阶段由前往后推移，直至终点。用标号法求解，先要设计标号。给节点j标号[(j，tij，zOj，Tj)]i，q，Ti，其中q为i所属阶段；Tj为由i到达j的时刻,Tj按式(4)～式(6)求得；Ti为到达i的时刻；tij为边(i，j)的权值；zOj为在时间tj到达节点j的目标值。这样，基于动态规划和标号法的求解步骤如下：

1) 对运输路网进行阶段的划分，得到阶段数Q，阶段q的节点集合记作Nq。

2) 给出出发时间t0，并给起点O以固定标号[(O，0，0，T0)]O，1，1，此时T0=t0，q= 1。

3) 寻求Nq和Nq+1中节点。Nq+1为Nq的前向节点集合，i∈Nq，j∈Nq+1，其中，i、j∈N，(i，j)∈E；获得阶段q的所有节点集合Nq。

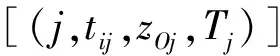
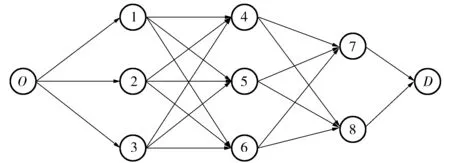
5) 令q=q+1，执行下一步。

6) 若q

7) 输出到终点D最小值，即min(Z)，并回朔获得出发时间为t0的最短路径。

4 算 例

将一个具体的运输案例，抽象为随机时变下运输路径选择问题。随机时变路网如图3。

图3 随机时变路网Fig.3 Stochastic time-dependent network

图3给出了从起点O到终点D之间的运输网络，各路段在不同时段所需的行驶时间如表1。其中A、B、C、u、d分别表示乐观时间、最可能时间、悲观时间、期望、方差。车辆在t0时，由O出发，到达目的地D，现希望寻求起点O到达目的地D所需行驶时间最少的线路。

表1 各条有向边在不同时段的运输时间Table 1 Transportation time of each directed edge at different time-zone /min

1) 通过给出的运输网络图，由前向后划分阶段，得到求解过程中各个阶段及其状态，如表2。

2) 给定出发时刻t0，利用文中所给算法，用MATLAB编程求解，计算对比车辆在t0时，由O行驶到D的最短路径和所需的最短时间。t0分别选取07：00、07：15、07：30，所得的最优解如表3。

表2 各个阶段和状态Table 2 Different stages and status

表3 不同出发时刻最短路径及其时间成本Table 3 The shortest path at different departure timeand its time cost

从表3可以看出，不同的出发时刻，所获得的最短路径时间成本以及行驶路径不同，所需行驶时间及最短路径会随出行时间的变化而变化。

5 结 语

笔者对随机时变路网环境中的运输行驶路线选择问题进行了研究，引入了三时估值法来处理路网的随机时变特性，建立了随机时变路网路线选择模型，构建了随机时变路网下的行程时间依赖函数，并设计了求解算法，研究结果表明：路段行驶时间及最短路径会随着出发时刻的不同而不同。

[1] 董振宁，张召生.随机网络的最短路问题[J].山东大学学报(理学版)，2003，38(3)：6-9.

DONG Zhenning，ZHANG Zhaosheng. The shortest path problems in stochastic and time-dependent network[J].JournalofShandongUniversity(NaturalScience)，2003，38 (3)：6-9.

[2] 范巍巍，程琳.随机路网的最短路径问题研究[J].公路交通科技，2007，24(9)：112-115.

FAN Weiwei，CHENG Lin. The study on shortest path problems in stochastic traffic network[J].JournalofHighwayandTransportationResearchandDevelopment，2007，24(9)：112-115.

[3] 郑龙，周经伦，易凡，等.大规模随机运输路网的路径优化[J].系统工程理论与实践，2009，29(10)：85-93.

ZHENG Long，ZHOU Jinglun，YI Fan，et al. Stochastic routing optimization of large-scale transportation network[J].SystemsEngineering-Theory&Practice，2009，29 (10)：85-93.

[4] 周光发，陈亮.随机网络最大概率路径问题的模型与算法[J].解放军理工大学学报(自然科学版)，2016，17(4)：391-395.

ZHOU Guangfa，CHEN Liang. Model and algorithm of maximum probability path problem in stochastic network[J].JournalofPLAUniversityofScienceandTechnology(NaturalScienceEdition)，2016，17 (4)：391-395.

[5] 贺政纲，宋金玉.时变条件下危险废弃物运输路径选择问题研究[J].中国安全科学学报，2014，24(12)：44-50.

HE Zhenggang，SONG Jinyu. Route planning for hazardous waste transportation as time varies[J].ChinaSafetyScienceJournal，2014，24(12)：44-50.

[6] 范文璟，马祖军.时变网络环境下城市应急救援路径优化[J].计算机应用，2011，31(增刊1)：125-128.

FAN Wenjing，MA Zujun. Optimization of rescue path for urban emergency in time-varying networks[J].JournalofComputerApplication，2011，31 (sup1)：125-128.

[7] 刘丽萍，斯剑栋，谢文成.时变条件下的危险品运输与应急救援双层规划研究[J].科学管理研究，2014，6(20)：208-213.

LIU Liping，SI Jiandong，XIE Wencheng. Research on bi-level programming of hazardous materials transportation and emergency rescue in time-varying network[J].ScienceandTechnologyManagementResearch，2014，6(20)：208-213.

[8] 彭勇，谢禄江，刘松.时变单车路径问题建模及算法设计[J].重庆交通大学学报(自然科学版)，2013，32(2)：263-266，334.

PENG Yong，XIE Lujiang，LIU Song. Route modeling and algorithm designing of time-dependent single vehicle[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2013，32(2)：263-266，334.

[9] 王莺，张治国，刘成华.时变条件下易逝品运输的路径选择[J].统计与决策，2009，10(10)：27-28.

WANG Ying，ZHANG Zhiguo，LIU Chenghua. Path selection of perishable goods transportation under time-varying conditions[J].StatisticsandDecision，2009，10 (10)：27-28.

[10] 陈京荣，俞建宁，李引珍.多属性随机时间依赖路网路径优化[J].西南交通大学学报，2012，47(2)：291-298.

CHEN Jingrong，YU Jianning，LI Yinzhen. Route optimization of multi-attribute random time-dependent road networks[J].JournalofSouthWestJiaotongUniversity，2012，47 (2)：291-298.

[11] 魏航，魏洁.随机时变网络下的应急路径选择研究[J].系统工程学报，2009，24(1)：99-103.

WEI Hang，WEI Jie. Emergency path problem in stochastic and time-varying network[J].JournalofSystemsEngineering，2009，24(1)：99-103.

[12] 曹慧，段征宇，陈川.随机时变路网环境下稳健路径选择及实证研究[J].交通运输系统工程与信息，2014，14(5)：194-201.

CAO Hui，DUAN Zhengyu，CHEN Chuan. Empirical research on robust optimal path problem in stochastic time-dependent networks[J].JournalofTransportationSystemsEngineeringandInformationTechnology，2014，14(5)：194-201.

[13] MALANDRAKI C，DASKIN M S. Time dependent vehicle routing problems：formulations，properties and heuristic algorithms[J].TransportationScience，1992，26(3)：185-200.

[14] SUNG K，BELL M G H，SEONG M，et al. Shortest paths in a network with time-dependent flow speeds[J].EuropeanJournalofOperationalResearch，2000，121(1)：32-39.

Transportation Route Selection in Stochastic Time-Dependent Network

LIU Shuai1，TANG Boming1，LIU Song2

(1. School of Civil Engineering，Chongqing Jiaotong University，Chongqing 400074，P. R. China; 2. School of Traffic & Transportation，Chongqing Jiaotong University，Chongqing 400074，P. R. China)

The travel time at each section of road transportation network was affected by traffic management，traffic congestion，weather changes and other uncertainties，so it showed stochastic time-dependent characteristics. The three-time valuation method in road network evaluation technique was introduced，and a path optimization model in stochastic time-dependent road network to minimize the travel time was established. A time-dependent function of the road sections when the vehicle travelled inter-temporally was proposed. Moreover，an algorithm of dynamically programming and labeling was designed to solve the function. Through a comparative analysis of the optimization results of the application examples，the effectiveness of the proposed model and algorithm was verified.

traffic and transportation engineering; stochastic time-dependent; over time; dynamic programming

10.3969/j.issn.1674-0696.2017.12.18

2016-12-19；

2017-09-26

教育部人文社会科学研究规划基金项目(17YJA630079)；重庆市人民政府发展研究中心项目(2016ZB-03)

刘 帅(1982—)，男，山东菏泽人，博士研究生，主要从事物流方面的研究。E-mail: wordday@sina.com。

唐伯明(1962—)，男，江苏东台人，教授，工学博士，博士生导师，主要从事交通运输工程方面的研究。E-mail: tbm@netease.com。

U491

A

1674-0696(2017)12-110-05

田文玉)