非均匀火灾作用下方形钢管混凝土短柱剩余承载力研究

焦 东

(辽宁工程技术大学建筑工程学院，阜新，123000)

非均匀火灾作用下方形钢管混凝土短柱剩余承载力研究

焦 东*

(辽宁工程技术大学建筑工程学院，阜新，123000)

为研究非均匀火灾作用下方形钢管混凝土短柱剩余承载力，在合理采用钢材和混凝土本构关系的前提下，基于ABAQUS建立了火灾后钢管混凝土柱相继热力耦合分析模型，并依据试验数据验证模型有效性。在此基础上进行了单面、相对两面受火状态下方形钢管混凝土短柱的轴压工作机理分析和参数分析，结果表明：受火方式对构件温度场及受力机理影响较大；受火时间、截面边长、防火保护层厚度是构件非均匀受火后剩余承载力的主要影响参数。在工程常用范围内，回归了两种受火方式下方钢管轴压短柱剩余承载力影响系数计算公式，可为该类构件在火灾后的修复提供参考。

钢管混凝土；短柱；非均匀受火；剩余承载力

0 引言

钢管混凝土结构具有承载力高、塑性和韧性好、经济效益高和施工方便等优点，随着其相关理论研究不断充实，钢管混凝土结构在高层建筑中的应用不断扩大。由于建筑结构朝着复杂化、使用多样化的方向发展，使得火灾安全隐患日益增多，因此火灾后钢管混凝土柱剩余承载力和加固修复研究具有重要意义。国内对于钢管混凝土柱火灾后剩余承载力研究已有丰厚成果：韩等[1- 2]进行了圆形、矩形钢管混凝土柱火灾后剩余承载力的试验研究，结果表明火灾后钢管混凝土的承载力损失严重，与常温下的承载力相比，长细比越大，构件火灾后承载力的损失率越高，并基于相关参数分析，提出了均匀受火方式下钢管混凝土柱剩余承载力实用计算方法。余和陶[3]进行了中空夹层钢管混凝土轴压短柱火灾后剩余承载力研究，结果表明在空心率相同的情况下，方套圆截面形式的试件其剩余承载力最高，而圆套圆截面形式的试件其延性最好。李和王[4]通过采用有限元软件对火灾全过程中方钢管混凝土轴压短柱进行了机理分析，并提出了方钢管混凝土轴压短柱剩余承载力简化计算公式。张等[5]进行了配筋钢管混凝土短柱火灾后剩余承载力试验，结果表明升温时间和构件截面尺寸是影响圆钢管钢筋混凝土轴压短柱火灾后剩余承载力的主要因素，并提出了圆钢管钢筋混凝土短柱火灾后剩余承载力的实用计算式。综上所述国内对于钢管混凝土柱的剩余承载力研究均基于均匀受火方式，而在实际工程中，因墙体的约束使得较多数柱子在火灾下处于非均匀受火状态，因此全部按照均匀受火状态进行剩余承载力计算显然不经济实用，因此本文基于有限元软件ABAQUS，建立两种典型非均匀受火(温度场单轴、双轴对称)方式下方形钢管混凝土短柱轴压力学分析模型，分析不同受火方式下构件的受力机理，并对构件火灾后剩余承载力具有潜在影响的因素进行参数分析，提出非均匀受火后方钢管混凝土柱剩余承载力计算公式，为后续相关试验研究及该类构件火灾后修复提供参考。

1 有限元模型及验证

正确选取材料热工、热- 力本构关系是后续分析的重要基础，经比对试算，本文选用Lie[6]提供的钢材和钙质混凝土热工参数计算式，对于混凝土中水分的影响，则通过调整比热容以考虑5%含水率的影响。文献[4]指出高温后混凝土及钢材的应力- 应变关系仍可以采用常温下的表达式，只需对弹性模量、峰值应力等参数在不同温度下进行修正，因此本文选用李[4]修正的高温后钢材和混凝土应力- 应变表达式。

热力耦合分析主要采用完全热力耦合分析和相继热力耦合分析两种方式，参考本文模型的特点，即温度场对力学分析影响较大，而力学分析结果对温度场影响较小，因此本文模型全部采用相继热力耦合分析模型。

各材料之间的接触取决于所进行的分析类型，为简化模型提高计算效率，温度场模型中的接触均设置为Tie连接，力学分析中混凝土与钢管的切向接触采用库伦摩擦，摩擦系数取值0.35，法向则按“硬接触”考虑。模型采用固接约束，即锁定三向位移和转角，柱顶放开轴向位移，使模型能够轴向压缩。

钢管混凝土柱在升温过程中，混凝土存在温度滞后的现象，即外界温度进入降温段，但内部混凝土仍有可能继续升温，这一现象主要是由于混凝土材料的热惰性所造成。为此通过ABAQUS的子程序USDFLD来实现材料积分点在升降温全过程所经历最高温度的读取[7]。

图1分别给出了文献[2,8]所进行的方形钢管混凝土短柱剩余承载力和温度测点试验结果与本文模型计算结果的对比，图1中有限元计算曲线与实测曲线拟合较好，具有良好精度。但也存在一定误差，主要是由于试验过程中的不确定性因素较多，如试验材料、试验设备和施工误差等，而模拟中的试件为理想状态，试验结果与模拟结果总会产生差异，但从图1c中可看出剩余承载力的拟合程度较好，因此本文模型能较精准的体现火灾全过程中钢管混凝土构件的温度和受力机理。

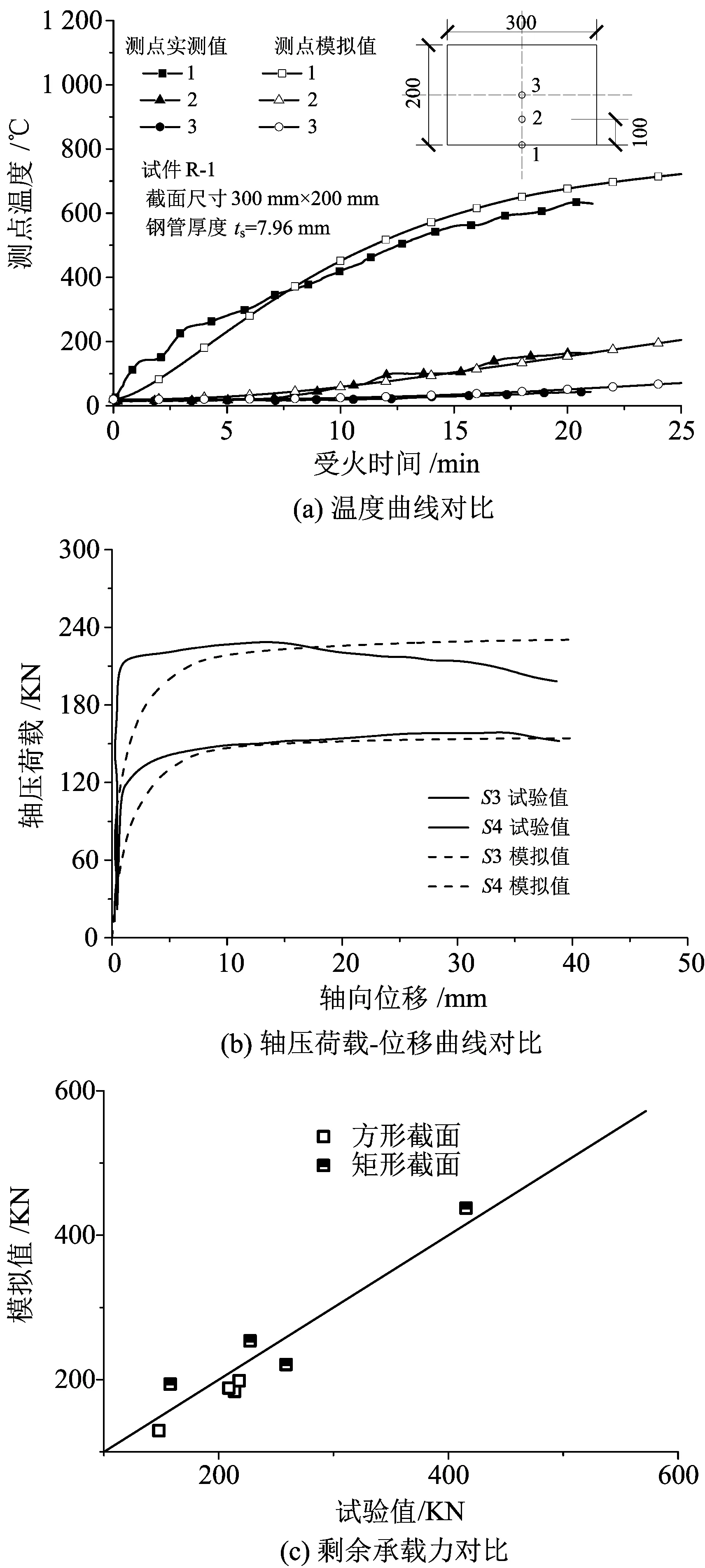
图1 有限元模型验证Fig.1 Validation of finite element model

2 非均匀受火后钢管混凝土短柱温度场及轴压受力机理分析

2.1 温度场典型算例

建立典型方钢管混凝土短柱温度场计算模型，探究火灾下构件横截面温度分布，受火形式采用单面、相对两面受火。相关模型参数为：截面边长B=300 mm，计算长度L=1200 mm、钢管厚度ts=4 mm、升温时间t=180 min，采用ISO- 834标准升降温曲线。

图2为两种受火方式下柱中截面温度场分布云图，可见受火方式对构件温度场分布起决定性作用。图2(a)为单面受火状态下柱中截面温度场云图，其特点为单轴对称分布，材料强度重心在对称轴上但偏向低温区，在轴压荷载作用下，这种温度格局易产生附加偏心。在相对两面受火作用下柱中截面温度云图呈双轴对称分布，各温度梯度为同心椭圆图形，且圆心处于截面形心，这种温度分布较单面受火状态下有益于构件受火后持载。两种受火方式下温度云图的共同点为：温度分布取决于受火方式；受火面附近混凝土温度较高，距离受火面越远，混凝土温度降低幅度很大，这是由于混凝土的良好吸热性和较差的导热性，受火面附近混凝土产生温度聚集现象。表1给出了不同时间和受火方式下，柱中截面各温度区域面积占横截面总面积的比值，从表1中可看出随着受火面及受火时间的增加，构件总体温度和升温速率明显提高，因此不同受火方式对构件材料剩余强度及轴压力学行为将产生不同影响。

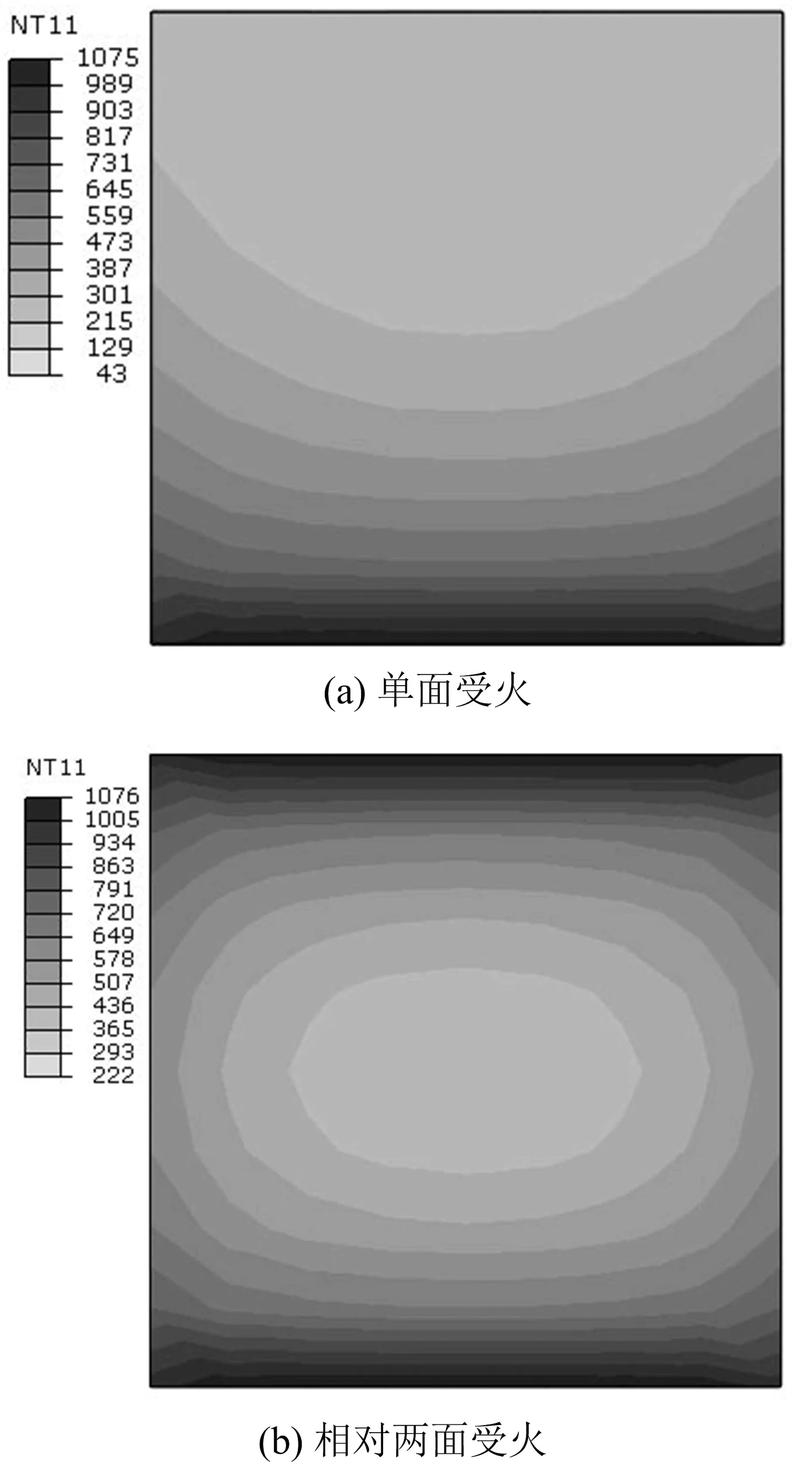
图2 不同受火方式下构件温度场云图(单位：℃)Fig.2 Temperature distribution under different fire exposure ways

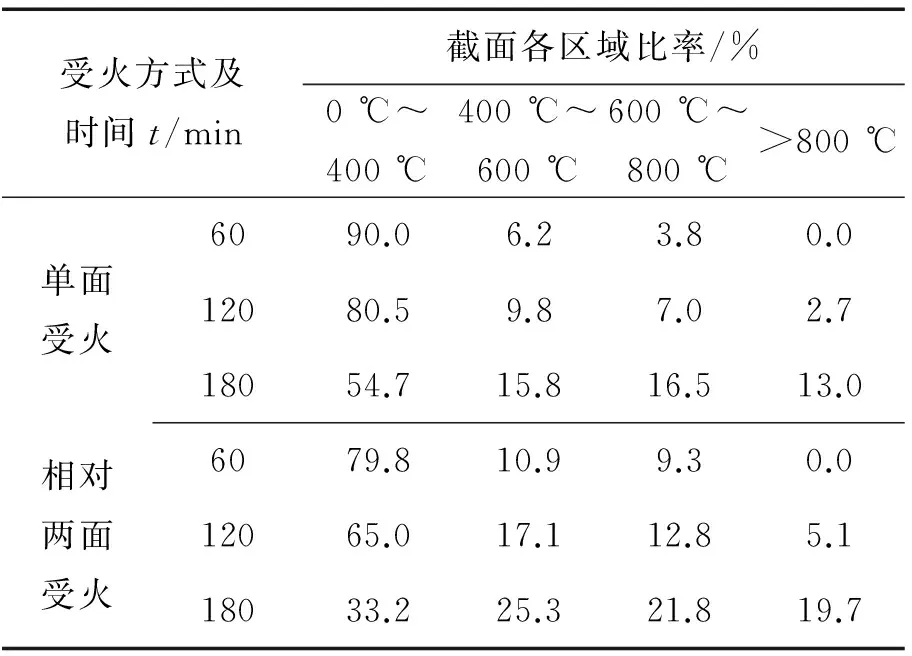
受火方式及时间t/min截面各区域比率/%0℃～400℃400℃～600℃600℃～800℃>800℃单面受火6090.06.23.80.012080.59.87.02.718054.715.816.513.0相对两面受火6079.810.99.30.012065.017.112.85.118033.225.321.819.7

图3 不同受火方式下横截面应力云图(单位：℃)Fig.3 Stress distribution of cross section under different exposure ways

采用两种不同受火方式升温180 min并降温后，施加轴压荷载，在到达临界屈服强度时构件柱中截面应力云图如图3所示。随着受火方式不同，柱中截面压应力也随之产生变化，并与其温度云图具有一定关联性。类似于温度场分布，单面、相对两面受火方式下构件应力仍为单轴对称和双轴对称分布，随着荷载逐渐增大，高压应力区逐渐向过火温度较低的混凝土区域移动，直至混凝土压碎破坏，整个应力演化过程简单，没有明显应力重分布。但单面受火的构件有明显的偏心，在轴压荷载作用下易产生附加挠度，使受火面附近混凝土提前压碎。由此可知虽然受火方式和受力机理均不相同，但经过两种受火方式升降温后，低温区混凝土对构件剩余承载力贡献较大。

3 参数分析及剩余承载力影响系数简化计算

为便于比较分析，定义非均匀受火方钢管混凝土轴压短柱剩余承载力影响系数：Kr=Nr/Nu,其中：Nu为常温钢管混凝土轴压短柱的极限承载力，选用文献[8]所提供的公式计算取值；Nr为受火后钢管混凝土轴压短柱的剩余承载力。对构件火灾后剩余承载力有潜在影响的因素有钢材强度、混凝土强度、含钢率α、受火时间t、截面边长B、防火保护层厚度a，本节对上述因素进行参数分析。

3.1 受火时间的影响

图4为系数Kr随受火时间的变化曲线。两种受火方式下，在35 min以内时，受火时间对系数Kr的影响较小，随着升温时间的增加，系数Kr逐渐减小。这是由于受火面较少以及升温初期温度较低，材料因火灾损失较小，系数Kr变化幅度不大，随着温度的增加，材料强度降低很快，系数Kr也急剧下降，且钢材所承受的力在剩余承载力中所占的比例也越来越大[9]，因此曲线后期有放缓的趋势。

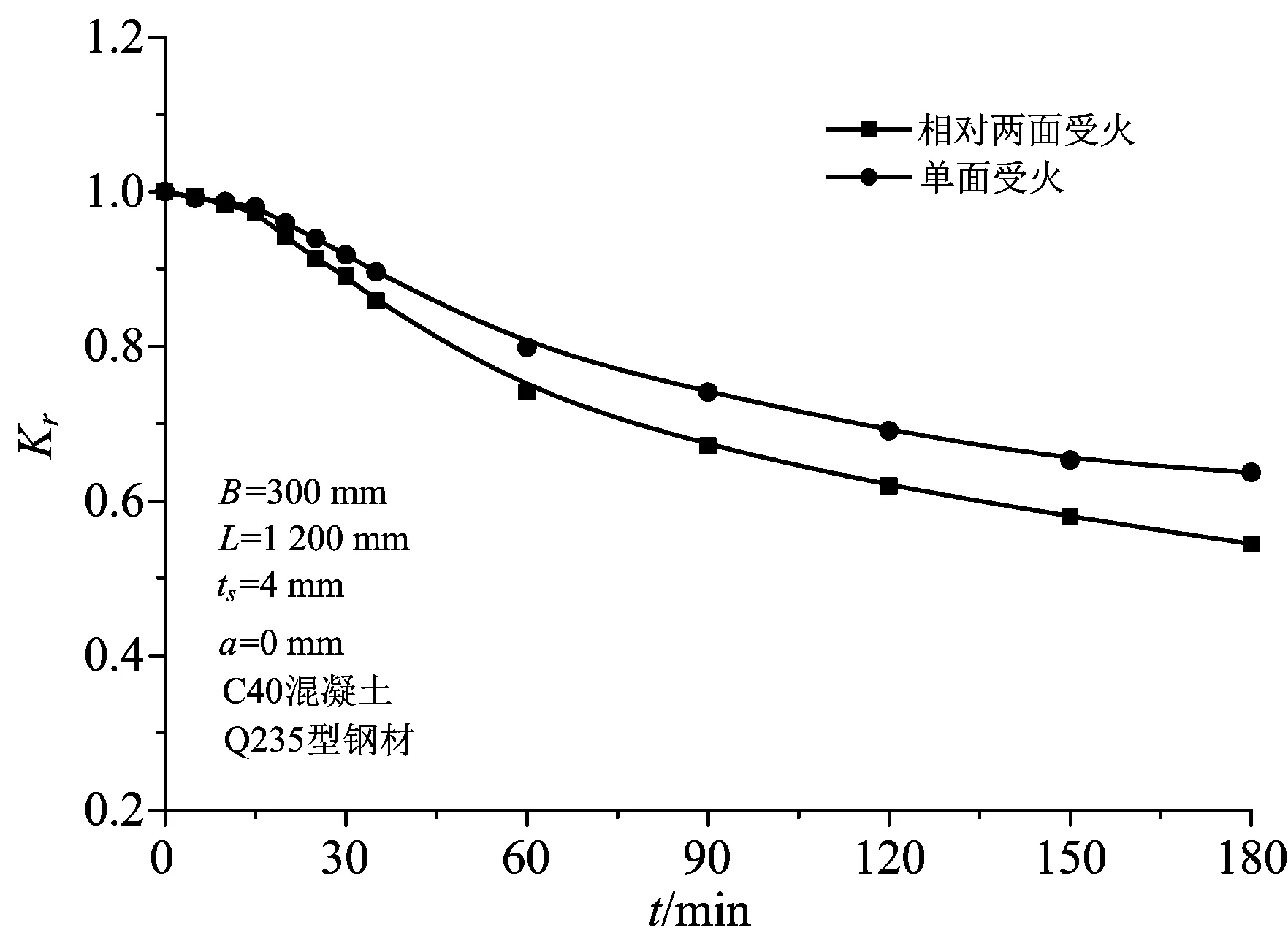
图4 受火时间的影响Fig.4 Effect of heating up time

3.2 混凝土强度的影响

图5为系数Kr随混凝土强度的变化曲线。由图5可知两种受火方式下，随着混凝土强度的增加，系数Kr变化较小，受火方式并没有对混凝土强度与系数Kr的关系造成影响，只是双面受火作用下系数Kr总体较小。这是因为混凝土强度虽然在增加，但在相同受火方式下，其常温极限承载力和火灾后剩余承载力也相应提高。

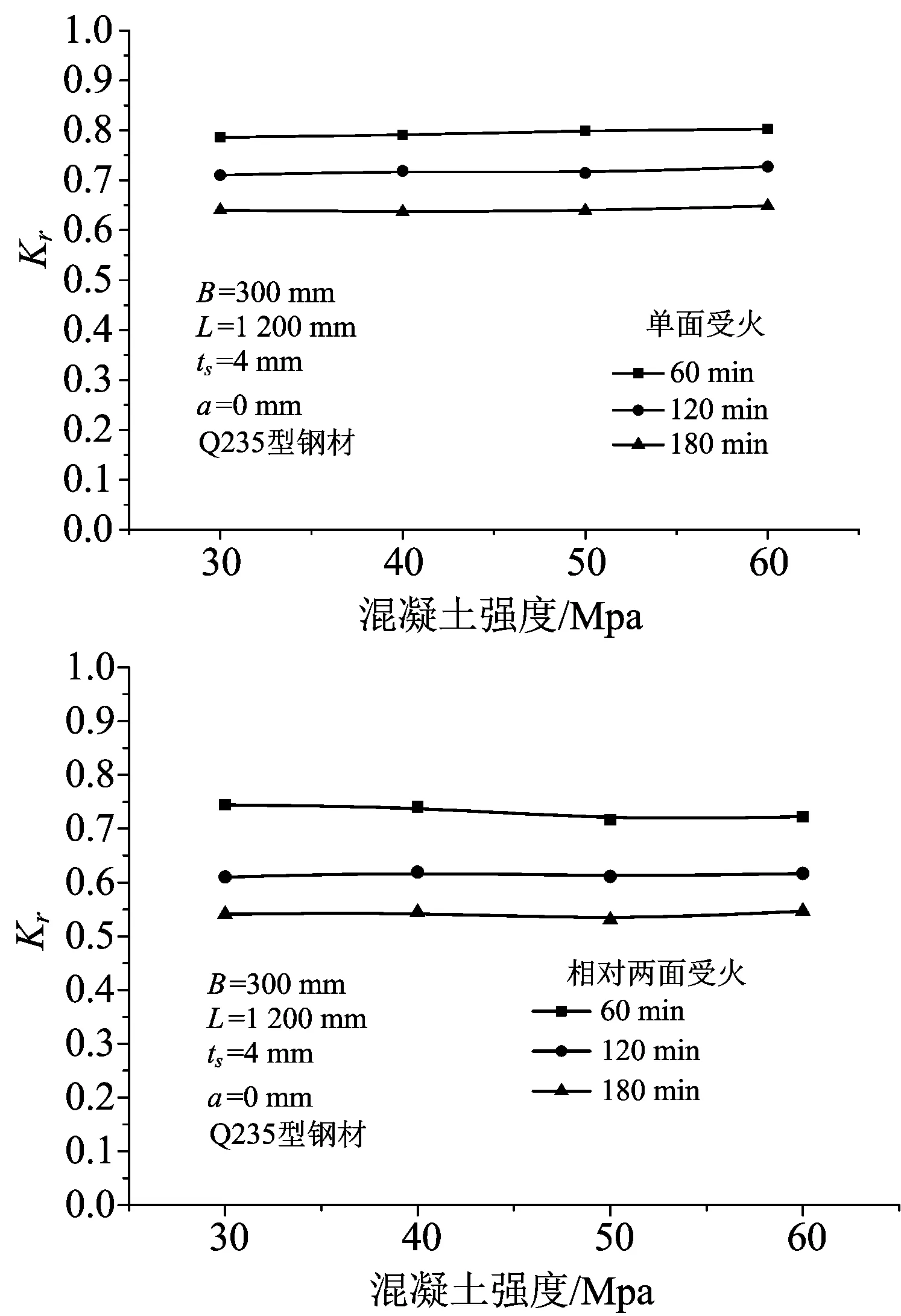
图5 混凝土强度的影响Fig.5 Effect of concrete strength

3.3 钢材强度的影响

图6为系数Kr随钢材强度的变化曲线，两种受火方式下随着钢材强度的增加，系数Kr变化较小。这是由于火灾后钢材强度会随着温度的升高而降低，承载力主要来自于混凝土，因此受火时间一定时，钢材强度对Kr影响很小。

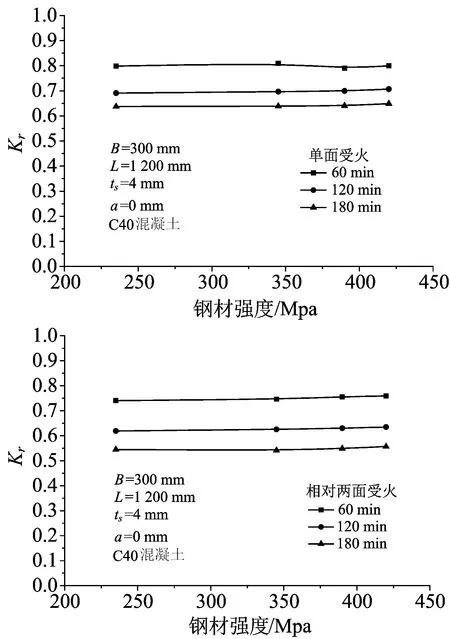
图6 钢材强度的影响Fig.6 Effect of steel strength

3.4 含钢率的影响

图7为系数Kr随含钢率的变化曲线，两种受火方式下随着含钢率的增加，系数Kr的变化幅度较小。含钢率增加的量占总面积的比率较小，且火灾后钢材强度损失较大，因此随着含钢率的增加，系数Kr小幅增加，总体变化幅度较小。

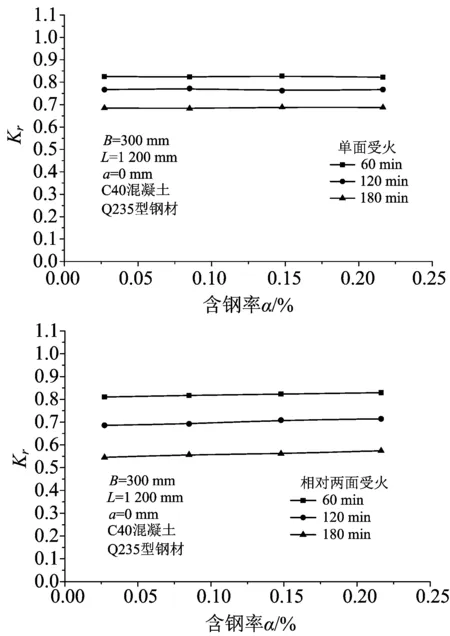
图7 含钢率的影响Fig.7 Effect of steel ratio

3.5 截面边长的影响

图8为系数Kr与截面边长的关系曲线，随着边长的增加，系数Kr变化明显。这是由于构件体积与截面边长呈正比，常温极限承载力随边长的增加大幅提高，但相同受火时间下，过火材料的体积占构件总体积的比率随着边长的增加而减小，因此图8中曲线呈上升趋势。但边长超过600 mm后曲线变缓，这是由于随着边长的持续增大，未受火材料所占总体积的比率不断增加，因此剩余承载力趋于常温极限承载力，即系数Kr趋于1。

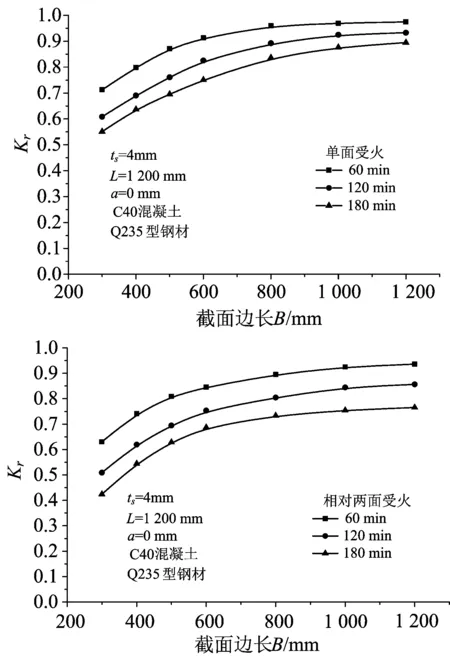
图8 截面边长的影响Fig.8 Effect of sectional dimension

3.6 防火保护层厚度的影响

图9为系数Kr随防火保护层厚的变化曲线，可见两种受火方式下，系数Kr随防火保护层厚度的增加呈上升趋势。这是由于非均匀受火方式下受火面积较少且防火保护层热阻较大，有效降低了构件内部温度，火灾后剩余承载力因此也相应提高。

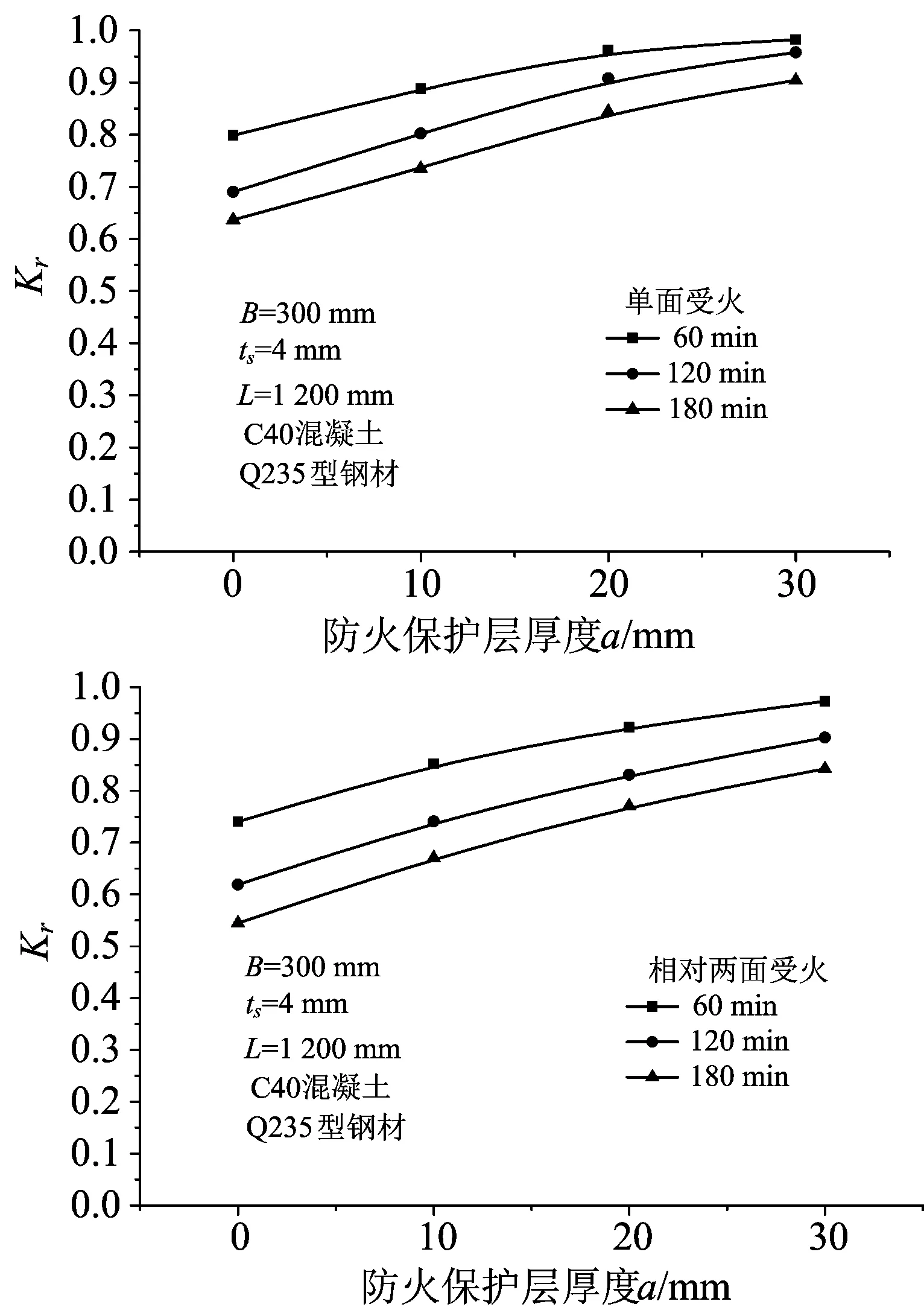
图9 防火保护层厚度的影响Fig.9 Effect of spray insulation thickness

3.7 剩余承载力影响系数简化计算

依据上节分析得知非均匀受火方式下，受火时间、截面边长、防火保护层厚度是构件火灾后剩余承载力的主要影响参数，并参照各参数对火灾后剩余承载力的影响曲线规律，确定公式中各参数的函数选用。因此通过对大量计算结果的整理归纳，得出系数Kr与受火时间、截面边长、防火保护层厚度有如下定量关系：

(1)

其中：

fk=f(t0)·f(a0)·f(B0)

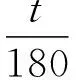
其中t为受火时间，min；a为防火保护层厚度，mm；B为截面边长，mm。

公式中参数见表2，建议公式适用范围：C30～C80混凝土、Q235～Q420钢材、截面边长B=300 mm～1200 mm、含钢率α=0.02～0.25、受火时间t=0 min～180 min、厚涂型防火保护层厚度a=0 mm～30 mm。图10为公式计算值与模拟值的比较情况，两者相关系数为0.989，均方差为0.02。

4 结论

1)受火方式直接影响了构件内部温度分布，因此对火灾后构件轴压受力性能产生一定影响。单面受火作用下构件温度云图为单轴对称，材料强度重心及高压应力区偏离构件形心，使得构件火灾后在轴压作用下容易产生偏心受力，不利于构件承重和灾后修复。相对两面受火作用下构件温度云图和轴压应力云图均为双轴对称，这种布局有利于构件火灾后承受轴压荷载。

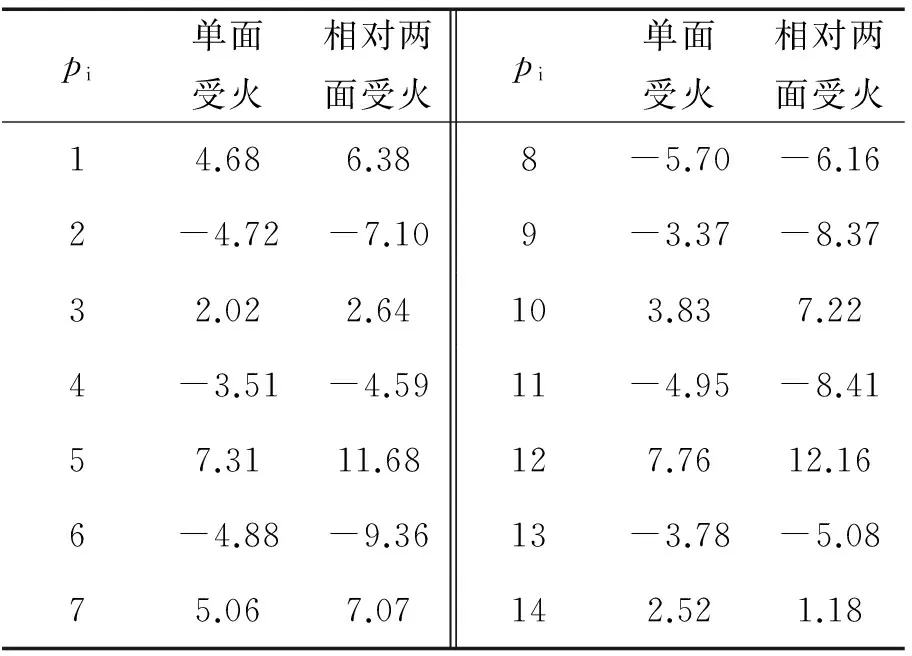
表2 参数P1～P14的取值

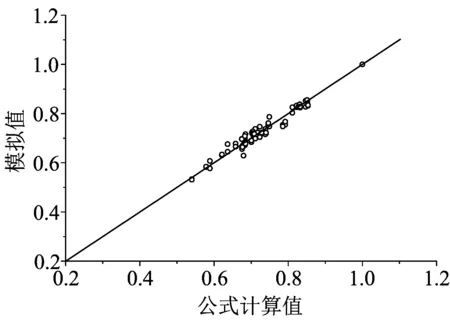
图10 简化计算结果与模拟结果的比较Fig.10 Comparison between simulation and calculated results

2)通过参数分析得知钢材强度、混凝土强度和含钢率对系数Kr影响较小，受火时间、截面尺寸、防火保护层厚度对系数Kr影响较大。

3)通过对大量计算结果进行归纳整理，回归出单面和相对两面受火作用后方钢管混凝土短柱剩余承载力影响系数Kr的简化计算公式，经对比得知公式具有一定精度，可为有关方钢管混凝土工程火灾后修复提供参考。

[1] 韩林海, 等. 标准火灾作用后矩形钢管混凝土柱剩余承载力的研究[J]. 工程力学, 2002, 19(5): 78- 86.

[2] 韩林海, 等. 钢管混凝土柱火灾后剩余承载力的试验研究[J]. 工程力学, 2001, 18(6): 100- 109.

[3] 余鑫, 陶忠. 中空夹层钢管混凝土轴压短柱火灾后剩余承载力的试验研究[J]. 工业建筑, 2009, 39(4): 9- 13.

[4] 李毅, 王志滨. 方钢管混凝土短柱的火灾后剩余承载力研究[J]. 水利与建筑工程学报, 2015, 13(6): 79- 84.

[5] 张玉琢, 等. 钢管钢筋混凝土短柱火灾后剩余承载力试验与有限元分析[J]. 防灾减灾工程学报, 2015, 35(6): 792- 798.

[6] Lie TT. Fire resistance of circular steel columns filled with bar- reinforced concrete[J]. Journal of Structural Engineering, ASCE, 1994, 120(5): 1489- 1509.

[7] 刘发起. 火灾下与火灾后圆钢管约束钢筋混凝土柱力学性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.

[8] 韩林海. 钢管混凝土结构: 理论与实践(第二版)[M]. 北京: 科学出版社, 2007: 509- 515.

[9] 张玉琢, 等. 火灾后配筋圆钢管混凝土柱剩余承载力数值分析[J]. 火灾科学, 2013, 22(3): 147- 151.

Residualladingcapacityofconcrete-filledsquaresteeltubestubcolumnsinnon-uniformfires

JIAO Dong

(College of Engineering and Architecture, Liaoning Technical University, Fuxin 123000, China)

This paper studies the residual capacity of concrete filled steel tubular short columns with square section in non- uniform fires. In terms of the proper constitutive relation of concrete and steel, a model of CFST columns coupling thermal and mechanical fields has been set up and the effectiveness of the models has also been verified by experimental data. Further, the mechanism and parameters of SCFST short columns under one side fire and opposite side fire are analyzed. The results show that the fire mode has a significant effect on components temperature field. Fire duration, length of cross section, covering thickness of fire protection are the main parameters which affect the residual capacity of components under non- uniform temperature field. Formulas with potential for engineering use are obtained by regression to calculate the residual capacity influence coefficient of CFST short columns under the two fire modes.

Concrete- filled steel tube; Stub column; Non- uniform fire; Residual lading capacity

1004- 5309(2017)- 00168- 07

10.3969/j.issn.1004- 5309.2017.03.06

2017- 02- 18；修改日期2017- 04- 05

焦东(1991- ),男，硕士，研究方向为大跨度空间结构。

焦东，E- mail: 34479647@qq.com

TU391;X932

A