基于多波束测深数据的GRID_DDM构建方法评估及分析
赵希亮,董 箭,张志衡,王利伟
(1.海军大连舰艇学院海洋测绘系,辽宁 大连 116018;2.海军大连舰艇学院 海洋测绘工程军队重点实验室,辽宁 大连116018;3.海军出版社,天津300450)
基于多波束测深数据的GRID_DDM构建方法评估及分析

赵希亮1,2,董 箭1,2,张志衡1,2,王利伟3
(1.海军大连舰艇学院海洋测绘系,辽宁 大连 116018;2.海军大连舰艇学院 海洋测绘工程军队重点实验室,辽宁 大连116018;3.海军出版社,天津300450)
系统分析了现有格网数字水深模型(GRID_DDM)插值数学模型的优劣,针对高精度、高密度多波束测深数据,采用不同的建模方法进行GRID_DDM构建,定量评估相关插值方法的精度与效率。实验表明,剖分插值和自然邻点插值方法构建的GRID_DDM精度较高,且效率可被接受,是多波束测深数据GRID_DDM构建的优选方法。
多波束测深数据;格网数字水深模型;精度与效率评估;适用性
格网数字水深模型(GRID digital depth model,GRID_DDM)是一种规则海底地形数字化表达模型。插值函数选择是GRID_DDM构建的核心问题,它贯穿在GRID_DDM的生产、质量控制、精度评定和分析应用等各个环节[1,2]。高精度、高密度多波束测深技术的出现为GRID_DDM构建提供了良好的数据基础,但多数研究主要针对相关方法本身展开,缺少对GRID_DDM构建方法的适用性研究,以及对其所构建GRID_DDM的精度和效率的评估[2,3]。
针对上述问题,本文将基于高精度、高密度多波束测深数据,采用不同的GRID_DDM构建方法,对GRID_DDM构建方法的精度和效率进行定量评估,分析相关方法在处理多波束测深数据方面的适用性,以期为海量高精度多波束测深数据的GRID_DDM构建方法选择提供一定的参考和借鉴,同时也为后续的多波束测深数据的处理和工程化应用奠定技术基础。
1 GRID_DDM插值数学模型
GRID_DDM插值就是根据若干相邻采样点的水深值估算待插点处的水深值。而任意一种插值方法都是基于原始海底地形起伏变化的连续光滑性,才能较可靠地由邻近采样点的水深插值出待插点水深值[3,4]。GRID_DDM插值的根本是对海底地形特征的认识和理解,方法则是待插点邻域范围、采样点权值以及插值函数关系的确定3方面的问题。GRID_DDM插值按待插点的分布范围,可分为整体插值、分块插值和逐点插值3种[4,5]。
1.1 整体插值数学模型
整体插值的基本思想是在整个研究区域上,用多项式或样条函数逼近地形曲面[1,3],如图1所示。整体插值通常要求地形采样点的个数大于或等于多项式的系数数目。当地形采样点的个数与多项式系数相等时,能得到唯一的多项式系数解。此时,多项式构建的地形曲面通过所有地形采样点,属于纯二维插值;当地形采样点的个数大于多项式系数时,多项式系数解不唯一。一般采用最小二乘拟合的方法求解多项式系数,此时的插值属曲面拟合插值或趋势面插值[4]。
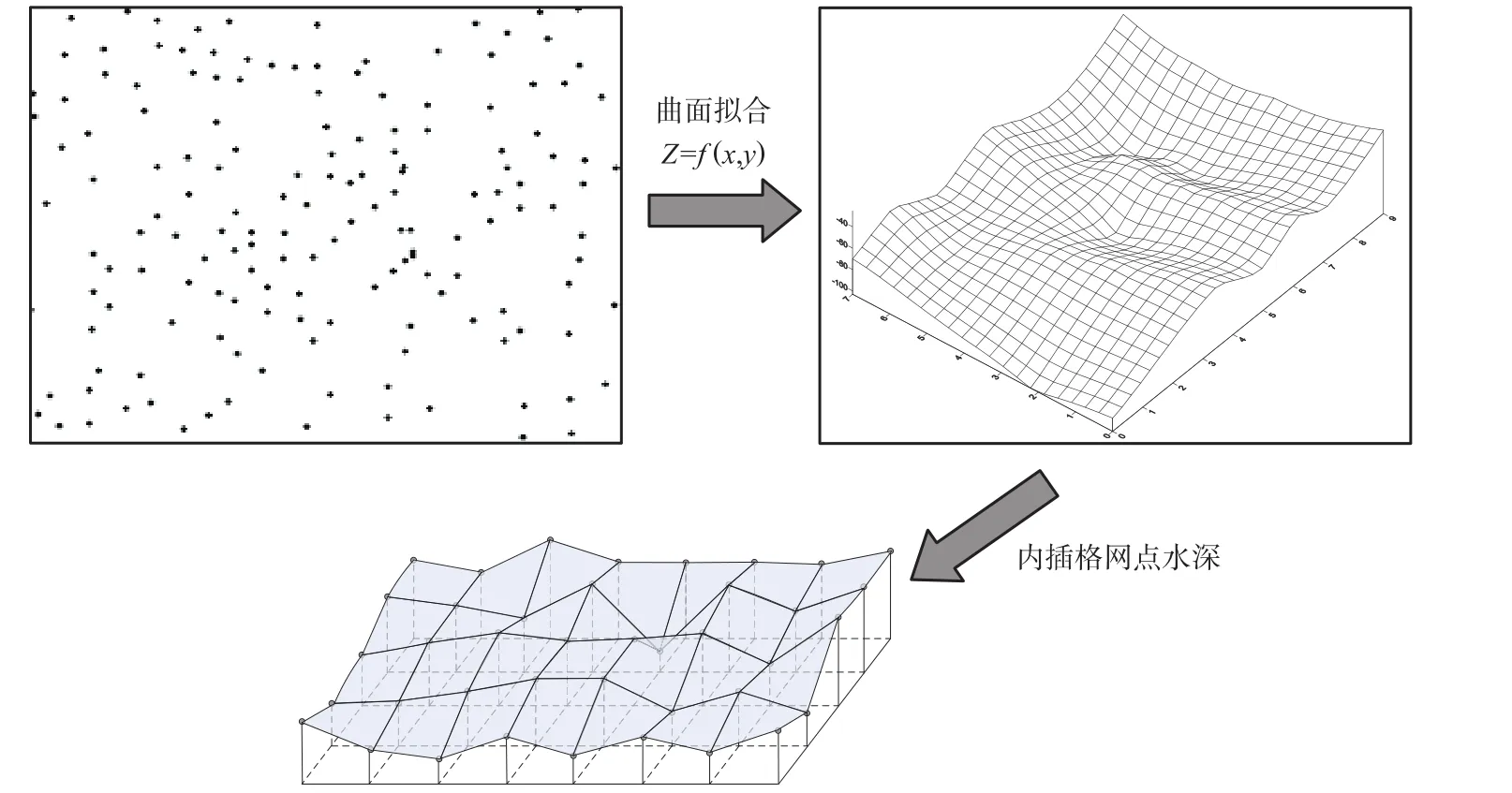
图1 整体插值示意图
整体插值函数保凸性较差,数值解不够稳定,解算速度较慢且不能提供插值区域的局部地形特征等,在实际工作中很少用于面向多波束测深数据的GRID_DDM 构建[1-4]。
1.2 分块插值数学模型
由于实际地形是很复杂的,整个地形很难用一个多项式来拟合。相关学者将复杂的整体地形分割成一系列局部单元,使这些局部单元内的地形曲面具有单一结构,利用简单曲面函数就可以较好地描述地形曲面。将地形区域按一定的方法进行分块,对每一块根据地形曲面特征单独进行曲面拟合和水深插值,称为GRID_DDM(局部)分块插值[4],如图2所示。此时,如何确保各分块之间曲面的连续性就成为分块插值必须考虑的重要问题。一般情况下,地形分块的大小是依据地形复杂程度、采样点密度及分布情况而定的。同时,为确保相邻分块间的平滑、连续拼接,相邻分块间要有一定宽度的重叠部分[1-4]。
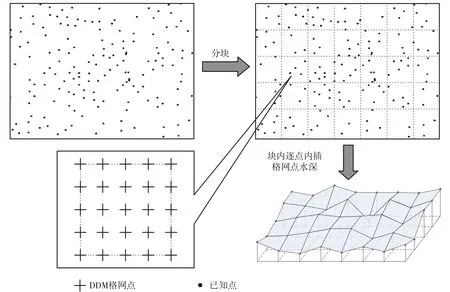
图2 分块插值示意图
典型的分块插值方法有二元样条函数插值、多层曲面叠加插值、最小二乘配置、克里金法、有限元法等[1-5]。
1.3 逐点插值数学模型
逐点插值就是以待插点为中心,确定一个邻域范围,用落在邻域范围内的采样点计算待插点的水深值[1-4]。逐点插值的本质是一种局部分块插值,但与局部分块插值又有所区别。逐点插值邻域范围中的采样点及分布状况会随着待插点位置的变动而变化,几乎每一个待插点的采样点集都是不同的,这较局部分块插值有更大的灵活性和地形适应性。同时,逐点插值法由于具有较高的插值效率而被广泛应用[1-5],如图3所示。
典型的逐点插值方法有移动曲面法、双线性曲面法、加权平均法、剖分插值、自然邻点插值等[4-11]。
1.4 GRID_DDM插值数学模型的分析比较
使用整体插值法,当选取的采样点数目较少时,不足以描述范围内的整体地形变化;而当选取的采样点数目较多时,则易出现振荡现象,很难获得稳定解。因此,在GRID_DDM插值中通常不采用整体插值的方法[1,4]。分块插值主要存在两个重要问题:一个是地形分块,目前难以运用智能的方法或自适应的方法对地貌形态识别后进行自动分块[2,4];另一个是要求解复杂的方程组,应用起来较为不便[3,4]。逐点插值方法计算简单,较为灵活,是目前比较常用的一种GRID_DDM插值方法。这种方法的主要问题是如何合理确定待插点邻域的范围,它不仅影响到GRID_DDM插值精度,也影响到插值效率[3-5]。
从目前的发展趋势来看,通过建立TIN(triangulated irregular network,TIN)进而生成GRID_DDM的方法(剖分插值)是较为普遍的方案,由于TIN能完全覆盖研究区域表面,可适应各种分布数据,并能方便地处理各种地形结构线、断裂线[4-6]。在所有生成TIN的方法中,Delaunay三角网最优,它能避免病态三角形的出现,常常被用来生成TIN[7-9]。基于Delaunay三角网的剖分插值方法(如图4a所示)已成为基于TIN的GRID_DDM构建的主要方法[10-11]。以Delaunay三角网直线对偶图Voronoi图为几何基础的自然邻点插值方法(如图4b所示)对于处理在空间上高度离散化分布的不规则采样点,以及描述由此造成的在空间尺度上剧烈变化的数字海底地形具有良好的效果[9,12]。
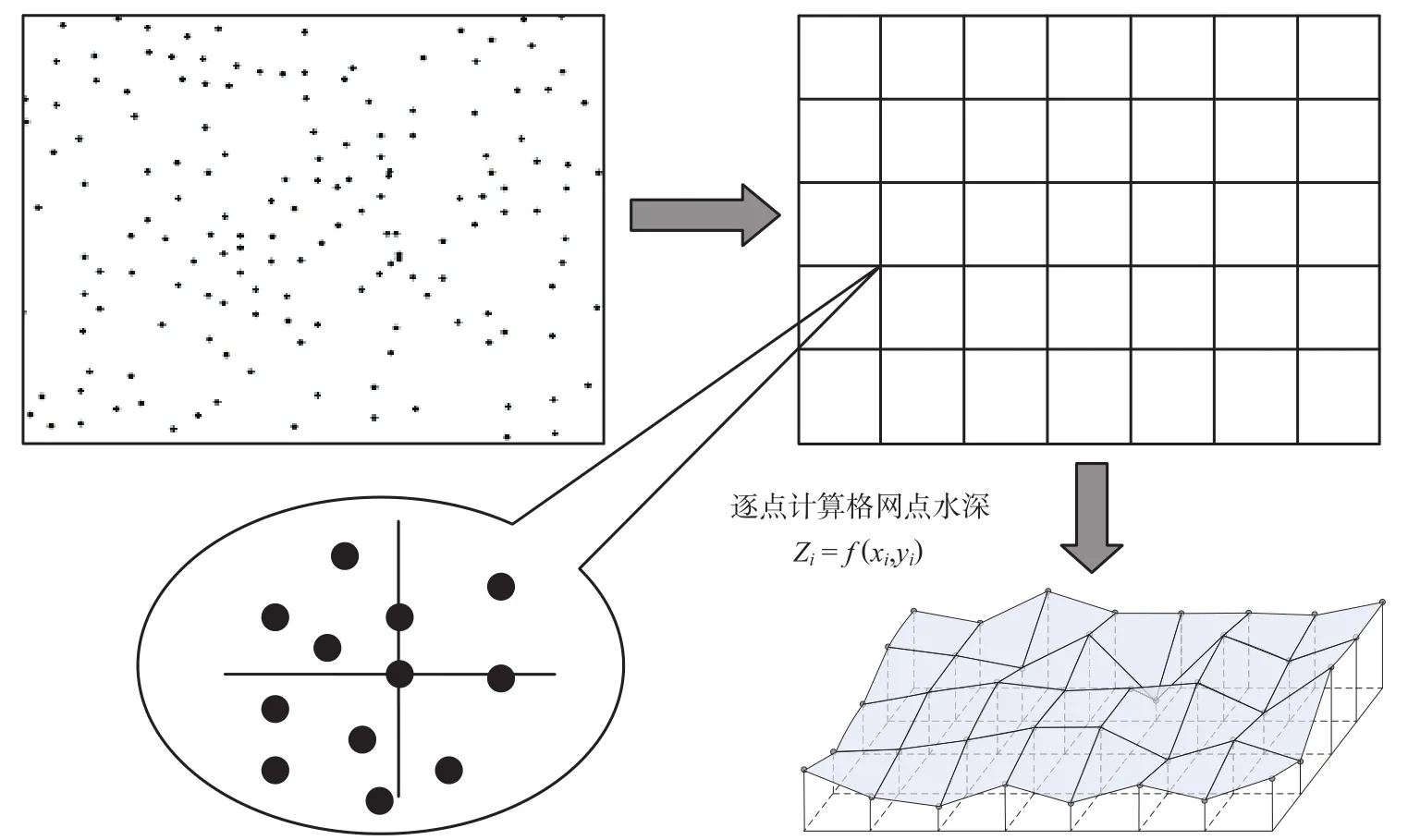
图3 逐点插值示意图

图4 剖分插值和自然邻点插值示意图
1.5 GRID_DDM精度评估方法
本文采用等深线回放法[1-4]和检查点法[3,13]来评估基于多波束测深数据构建的GRID_DDM精度。
等深线回放法是将构建的GRID_DDM插值生成等深线,再目视检查,并与其他方法生成的等深线进行比较,属于定性评估。检查点法是选择并预留一定数量分布均匀、合理的水深点作为检查点,其水深值为Zi(i=1,2,…,n),则GRID_DDM精度(标准方差)为:
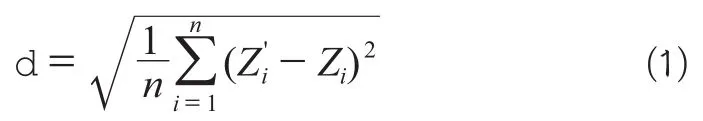
其中,Zi'(i=1,2,…,n)表示由构建的GRID_DDM插值出的检查点Zi处的水深值。
2 实验结果与分析
实验采用的数据为我国东海某泥沙底质海区的多波束测深数据,共包含12 774个离散水深点,极限误差为1 m,GRID_DDM大小设置为100×87。其中移动曲面法、双线性曲面法和加权平均法中参与待插点计算的采样点数目为8;剖分插值中待插点的计算采用线性插值,自然邻点插值中插值函数选用Sibson插值。实验环境为Core(TM) i5处理器,主频为2.8 GHz,内存为2 G。表1所示分别为基于上述不同插值方法的海底地形表面及等深线(等深距为5 m)对比图。
由表1可以看出,相对于前3种插值方法,后2种插值方法生成的等深线在保留海底细部地形特征方面的优势较为明显。此外,为验证各种插值方法在插值精度上的差异,依据式(1)并借助Surfer8.0软件的残差分析功能,对各种插值方法的实验结果进行量化分析,同时记录不同方法构建GRID_DDM的运行时间,结果见表2。
由表2可以看出:①移动曲面法和双线性曲面法插值效率较低,且拟合曲面针对海底地形变换剧烈的情形并不完全适用,造成这两种方法的插值精度也相对较低;②加权平均法具有较高的插值效率,由于这种方法未充分考虑离散分布采样点组合带来的海底局部地形形态变化影响,尽管相对于移动曲面法和双线性曲面法在插值精度上有所提高,但仍超出了水深测量的极限误差;③剖分插值和自然邻点插值方法由于在水深插值时利用了Delaunay最优三角形(Voronoi单胞)的几何特性,具有较高的插值精度,且均小于水深测量的极限误差。这两种方法需生成待插点附近离散采样点的Delaunay三角网(Voronoi图),相对于无任何约束的加权平均法,插值效率略低。由此得出,加权平均法在处理大数据量的多波束测深数据时,尽管插值效率优势明显,但插值精度并不能完全满足GRID_DDM构建的要求;剖分插值和自然邻点插值方法的插值效率在所有实验插值方法中虽不明显占优,但插值精度优势明显,可作为面向多波束测深数据的GRID_DDM构建的优选方法。

表1 基于不同插值方法的海底地形表面及等深线对比图
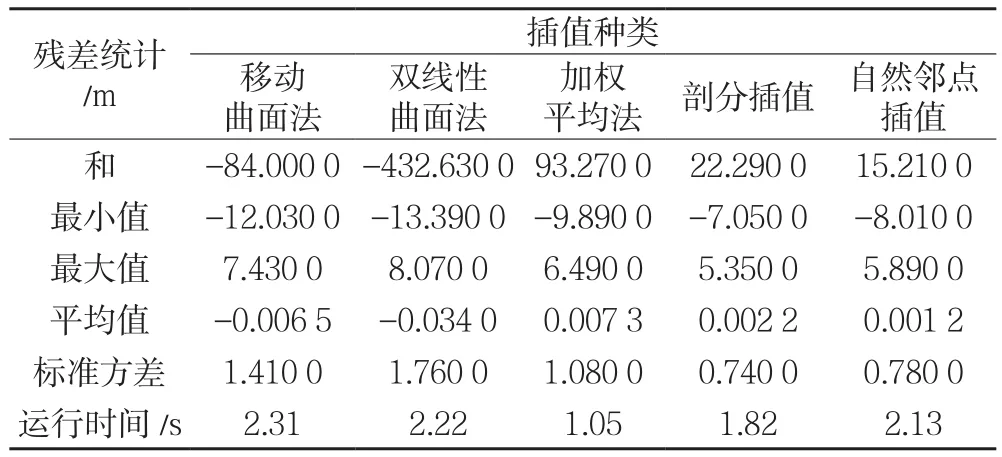
表2 不同插值方法的精度与效率比较
3 结 语
针对多波束测深数据,利用不同的GRID_DDM构建方法生成指定分辨率下的GRID_DDM,定量分析相关方法的精度和效率。实验结果表明,不同的GRID_DDM构建方法,所构建的GRID_DDM在精度和效率方面的差异较大;剖分插值和自然邻点插值方法由于在方法设计时充分利用了Delaunay最优三角形(Voronoi单胞)的几何特性,顾及了离散分布采样点组合带来的海底局部地形形态变化影响,具有较高的插值精度,且插值效率相对于其他方法可被接受,是多波束测深数据构建GRID_DDM的较好方法。
本文仅针对复杂的泥沙底质海区(属于中度复杂海底地貌)进行分析实验,下一步将结合不同类型、不同复杂程度的海底地形数据研究GRID_DDM构建方法的适用性,并结合海底地形特征线(如山脊线、谷底线)的提取进一步提高GRID_DDM构建精度。
[1]陈轶. 数字水深模型的构建及多尺度表达研究[D].大连:海军大连舰艇学院, 2011
[2]胡海, 游涟, 胡鹏, 等. 数字高程模型内插方法的分析和选择[J].武汉大学学报(信息科学版),2011,36(1):82-85
[3]李志林, 朱庆. 数字高程模型[M].武汉: 武汉大学出版社,2008
[4]汤国安, 刘学军, 闾国年. 数字高程模型及地学分析的原理与方法[M].北京:科学出版社, 2005
[5]周启鸣, 刘学军. 数字地形分析[M].北京: 科学出版社, 2008
[6]胡金星, 马照亭, 吴焕萍, 等. 基于格网划分的海量数据Delaunay三角剖分[J].测绘学报,2004,33(2):163-167
[7]陈军. Voronoi动态空间数据模型[M].北京:测绘出版社,2002
[8]谭仁春,杜清运,杨品福,等.地形建模中不规则三角网构建的优化算法研究[J].武汉大学学报(信息科学版),2006,31(5):436-439
[9]田峰敏,徐定杰,赵玉新. 一种建立海底格网数字高程模型的插值方法[J].中国航海, 2009,32(3):61-65
[10]郑顺义,邓德彦. 基于三角网无缝拼接的三维重建[J]. 武汉大学学报(信息科学版), 2009,34(1): 15-18
[11]谭兵,蒋定华,许素芹.一种顾及地形特征的DEM内插方法[J].测绘学院学报,2001,18(9):26-28
[12]高洋,张健. 基于自然邻点插值的数据处理方法[J].中国科学院研究生院学报, 2005,22(3):346-351
[13]杜明成. 海底地形数据获取的手段、精度和用途[J].专题探讨, 2009(9):64-69
P229
B
1672-4623(2017)12-0085-04
10.3969/j.issn.1672-4623.2017.12.027
2017-02-22。
国家自然科学基金资助项目(41601498)。
赵希亮,硕士,讲师,主要从事海图生产质量研究。

