兰州市安宁区彩钢棚空间分布特征及分析
李鹏元,杨树文,3,杨玲莉 ,闵 霄,张 珊
(1.兰州交通大学测绘与地理信息学院,甘肃 兰州 730070;2.甘肃省地理国情监测工程实验室,甘肃 兰州 730070; 3.甘肃省遥感重点实验室, 甘肃 兰州 730000)
兰州市安宁区彩钢棚空间分布特征及分析

李鹏元1,2,杨树文1,2,3,杨玲莉1,闵 霄1,张 珊1
(1.兰州交通大学测绘与地理信息学院,甘肃 兰州 730070;2.甘肃省地理国情监测工程实验室,甘肃 兰州 730070; 3.甘肃省遥感重点实验室, 甘肃 兰州 730000)
基于平均最近邻、标准差椭圆、核密度等分析方法,研究了用于民用临时住房的小型彩钢棚和工业用大型彩钢棚的空间分布特征。实验结果表明,安宁城区小型彩钢棚、大型彩钢棚在空间中都呈聚集性分布,且两者分布方向为东南-西北轴向,但彩钢棚在不同区域的分布密度却有明显差异。总体反映出安宁城区结构深受地理环境、交通状况以及政府决策的影响,城市的经济发展仍相对滞后,城区内部亟待改造升级。
彩钢棚;空间分布;平均最近邻;标准差椭圆;核密度
城市空间结构是城市中物质环境、功能活动和文化价值等组成要素之间关系的表现方式,其理论主要包括城市物质空间结构、城市经济空间结构、城市社会空间结构3个方面[1],从研究尺度可分为宏观和微观两个层次。宏观层次的城市物质空间结构研究起步较早,在测度方法、形态类型评价、空间紧凑度、空间增长特征、演变机制方面有大量成果出现[2-4]。微观层次的城市物质空间结构研究是指通过分析某一单一景观的空间分布特征,并从中反演出与此相关的城市形态[5-9]。 彩钢棚是近年来大量涌现的一种重要城市地物,其空间分布与城市自身的结构形态关系密切。本文尝试通过分析彩钢棚这一独特空间要素的分布格局,以此挖掘城市有价值信息。
1 彩钢棚信息的获取
安宁区位于兰州市西北部,东与城关区相接,西与西固区毗邻,南临黄河,北依群山。其影像如图1所示,该影像是2015-07-28获取的GF-1影像。前期已构建了基于知识规则的彩钢棚决策树提取模型,根据该模型和算法提取的兰州市安宁区彩钢棚信息如图2所示。

图1 安宁区GF-1遥感影像
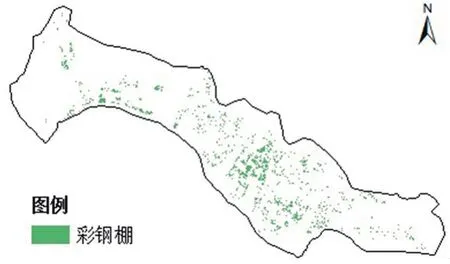
图2 安宁区彩钢棚信息
2 要素空间分布特征分析方法
要素在空间中有聚集或分散、分布重心、分布方向、在不同区域的分布密度等诸多特征,本文选用平均最近邻、标准差椭圆、核密度等分析方法分别对要素的这些特征作出研究。为方便分析,研究对象都简化为点要素(面状要素用质心代替)。
2.1 平均最近邻分析
平均最近邻用于评价要素在空间中是否具有聚集性分布特性。分析的过程是:先计算每个点与最邻近点的距离,再求解所有最近距离的平均值,可用观测平均最近邻距离计算:

式中,n表示点要素数量,di表示第i个要素与最邻近要素的距离。点集在随机分布情形下的预期平均距离是:

式中,A表示围成点集的包络线面积。当观测平均最近邻距离小于预期平均距离时,认为要素在空间中具有聚集性分布特征,反之呈离散分布。实际计算中,常通过平均最近邻指数NNI衡量:

显然,NNI<1时要素为聚集性分布。
2.2 标准差椭圆分析
标准差椭圆是分析点数据分布方向的常用工具,它由以下几个要素构成:转角θ、沿长轴的标准差和沿短轴的标准差[10]。转角θ可以看作是笛卡尔坐标系下x轴和y轴按照点集分布的地理方位沿一定角度旋转后,正北方向与顺时针旋转的长轴之间的夹角。标准差椭圆的计算公式如下:

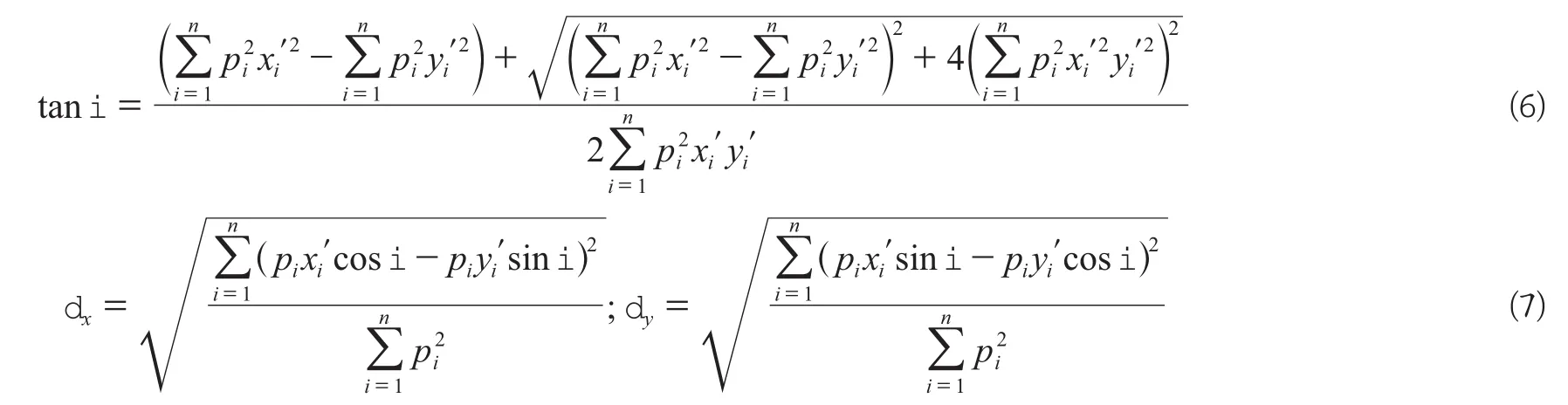
式中,(xi, yi)是点i的坐标;pi是点的权值,(xc, yc)是点集的重心。式(6)中,根据tanθ可以得到点分布格局的转角。式(7)中,δx、δy分别为沿x轴的标准差和沿y轴的标准差[11]。椭圆面积反映要素的分布范围大小;长轴与短轴之比越大,要素分布的方向性越强。
2.3 核密度分析
核密度估算方法主要借助一个移动窗口,计算并输出每个栅格单元的点密度。一般定义为[7]:设x1,…xn是从分布密度函数为f的总体中抽取的独立同分布样本,估计f在某点x处的密度值f (x),通常有Rosenblatt-Parzen核估计:
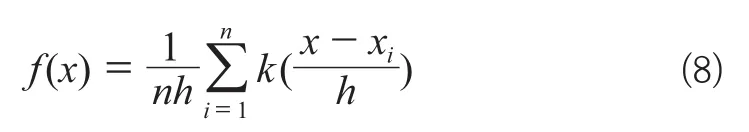
式中,k()为核函数;h>0,为带宽,(x−xi)为估计点到样本xi处的距离。
3 彩钢棚空间分布特征分析
3.1 描述性统计
据统计,安宁区彩钢棚共4 817件,总面积2 770 332 m2,占全区土地面积的4.031%。其中最大彩钢棚24 700 m2,最小彩钢棚16 m2,平均面积575 m2,表明彩钢棚大小差异悬殊,这种差异是由彩钢棚的用途决定的。实地调查结合影像分析得出,面积大于500 m2的彩钢棚常用于物流存储和工业生产,而小于这一阈值的彩钢棚多是居民、建筑工人临时住房或其他用途房屋。在后文中,分别简称为大型彩钢棚和小型彩钢棚。进一步统计,大型彩钢棚与小型彩钢棚的数量之比约为3︰20,面积之比是8︰5,即小型彩钢棚在数量方面居于主导地位,而面积上大型彩钢棚占优。
3.2 彩钢棚聚集性分析
大型彩钢棚与小型彩钢棚在城市中表征的意义不同。表1是计算得到的彩钢棚平均最近邻结果,表中小型彩钢棚与大型彩钢棚的最近邻指数小于1,说明两者在空间中都呈聚集性分布。但观测平均距离前者比后者小,表明小型彩钢棚的分布较大型彩钢棚密集。

表1 平均最近邻分析结果
3.3 彩钢棚分布方向分析
以彩钢棚面积作为权重字段,计算标准差椭圆参数见表2,显示如图3(图中蓝色质心点表示小型彩钢棚,红色质心点表示大型彩钢棚)。结合图表得出,小型彩钢棚在全区的分布范围较大型彩钢棚广泛;小型彩钢棚与大型彩钢棚的主要扩散方向是东南-西北轴向,且大型彩钢棚的这种扩散趋势更显著;与小型彩钢棚比,大型彩钢棚的分布重心偏西。

表2 标准差椭圆参数
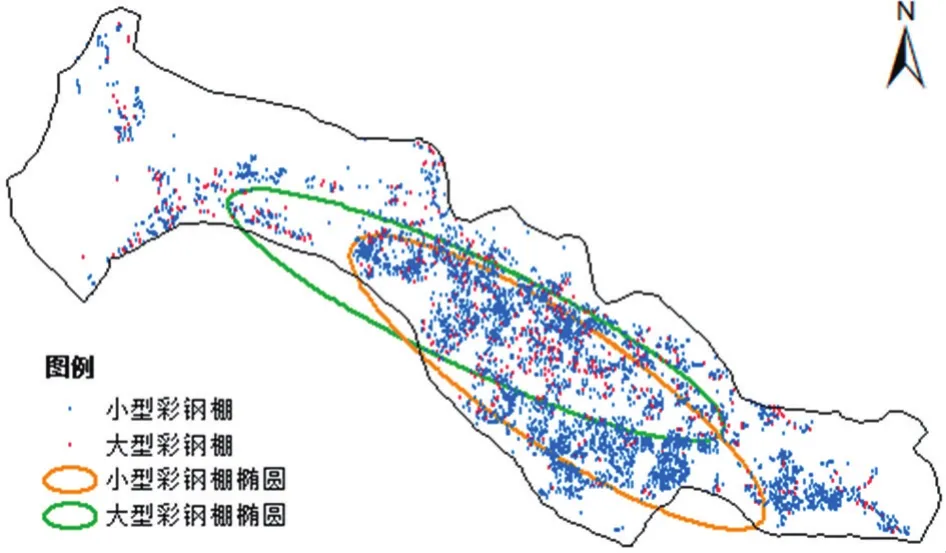
图3 标准差椭圆分析结果
3.4 彩钢棚密度分析
平均最近邻、标准差椭圆从整体上描述了彩钢棚的分布状况。为详细了解彩钢棚在不同区域的分布特点,对其进行核密度分析,图4、5是以彩钢棚面积作为计算字段得到的分析结果。在分析之前,用主要道路网对安宁区进行区域划分,图中的粗黑线条表示区内的主要道路,这种划分方法与传统的网格划分、等扇划分以及象限划分相比,更具有灵活性、符合当地实际情况。图中主要道路结合行政区边界将当前城市划分为了Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ共6大块区域。Ⅰ区域是政府所在地且人口密集,因此作为中心地带;Ⅱ、Ⅲ靠近中心,是次中心区域;Ⅳ与中心隔开,故作为次边缘地带;Ⅴ、Ⅵ离中心最远,属边缘地带。图4中小型彩钢棚在次中心、次边缘、边缘地带都有高密度分布,而尤以Ⅱ次中心区域高密度分布范围最广。图5显示出大型彩钢棚在城区次中心地带有零散的高密度分布,至最边缘地带高密度分布范围加强,但大面积的密集分布出现在Ⅳ次边缘地带。图4、5共同反映出小型彩钢棚与大型彩钢棚在Ⅴ、Ⅵ边缘区域有沿道路两侧分布的趋势。

图4 小型彩钢棚核密度分析结果
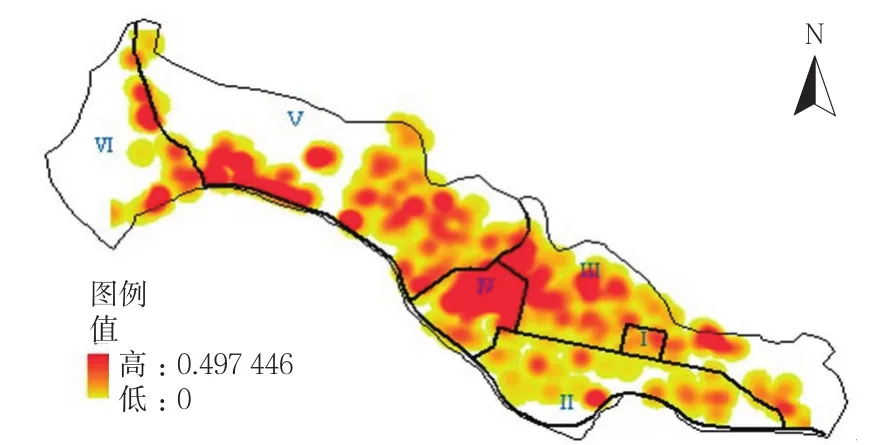
图5 大型彩钢棚核密度分析结果
4 彩钢棚与城市间的联系
彩钢棚在城市的构成要素中占据重要地位。其中,小型彩钢棚在区内分布广泛,在次中心地带更呈现大片密集型分布。实地走访了解到,此类连片区属“城中村”。“城中村”是城市化进程中未待开发的农村村落或居民区域,表明安宁区由农村转化而来的特征明显,且目前仍处于过渡阶段。考虑到彩钢易燃的特性,这类区域需加强火情检测。
大型彩钢棚集中于城区次边缘地带,这是市场和政府决策共同作用的结果。在城市中心,土地价格昂贵,建设大型彩钢棚成本较高,同时部分工业生产过程会对环境产生危害,使大型彩钢棚在市区的建设不适宜。需要指出的是,大型彩钢棚的多少并不是衡量一个地区工业能力的指标,因工业生产不总是依赖彩钢棚实现,但若结合土地利用现状图可知,大型彩钢棚与一般工业生产建筑具有亲和性,故大型彩钢棚的空间分布特征能间接反映出地区的工业布局。
在城市最边缘地带,大型彩钢棚与小型彩钢棚往往同时出现,这种小型彩钢棚区别于中心地带的棚户区房屋,它常作为工人临时住所,代表城市的建设力量。为方便与城区的联系,两类彩钢棚都趋向道路两侧分布。根据GF-1遥感影像,此地带的地理构成要素主要有绿地和山地,彩钢棚在这种特殊地带内的扩展存在一定的局限性,这也表明安宁区在未来一段时间的城市扩展会放缓。
5 结 语
针对彩钢棚空间分布与城市结构和发展存在联系这一现实,通过平均最近邻、标准差椭圆、核密度分析等方法分别研究了大型彩钢棚与小型彩钢棚在城区中的空间分布格局。结果表明,小型彩钢棚、大型彩钢棚空间分布特征既有相同点,也有不同点,这些特征反映出安宁城区的空间形态和发展现状。
[1]周春山,叶昌东.中国城市空间结构研究评述[J].地理科学进展,2013,32(7):1 030-1 038
[2]Batty M, Xie Y. From Cells to Cities[J]. Environment and Planning B: Planning and Design, 1994, 21(7):31-48
[3]周春山,叶昌东.中国特大城市空间增长特征及其原因分析[J].地理学报,2013,68(6):728-738
[4]吴启焰.城市密集区空间结构特征及演变机制[J].人文地理,1999,14(1):11-16
[5]Syamwll I B,Tanimura P H. The Spatial Distribution of Japanese Manufacturing Industries in Indonesia[J]. Review of Urban &Regional Development Studies,2000, 12(2):121–135
[6]雷一鸣,陈曦,杨辽,等.基于Worldview-2的乌鲁木齐城区绿地空间格局分析[J].干旱区研究,2015, 32(6):1 233-1 239
[7]蔡雪娇,吴志峰,程炯.基于核密度估算的路网格局与景观破碎化分析[J].生态学杂志,2012,31(1):158-164
[8]杨永春. 兰州城市建筑的空间分布[J].世界地理研究,2008,17(1):39-46
[9]王士君,浩飞龙,姜丽丽.长春市大型商业网点的区位特征及其影响因素[J].地理学报,2015,70(6):893-905
[10]赵媛,杨足膺,郝丽莎,等.中国石油资源流动源-汇系统空间格局特征[J].地理学报,2012,67(4): 455-466
[11]Wong W S D,Lee J.Statistical Analysis of Geographic Information with ArcView GIS and ArcGIS[M]. Wiley,2005
P208
B
1672-4623(2017)12-053-03
10.3969/j.issn.1672-4623.2017.12.017
2016-09-29。
甘肃省科技计划资助项目(1506RJZA070,148RJZA028);甘肃省高等学校科研资助项目(2015A-049);甘肃省遥感重点实验室(寒旱所)开放基金;兰州市人才创新创业项目共同资助(2015-RC-28)。
李鹏元,硕士研究生,主要从事遥感图像信息识别方面研究工作。

