基于层次变权的物流网络流量分配模型

周晓

福建江夏学院工商管理学院,福建 福州 350108

随着经济全球化的不断深入，物流对社会经济发展的推动作用日益凸显。物流网络是物流活动开展的载体，网络静态的结构布局和动态的货流量分布都会对物流效率和效益产生影响。如何在静态的物流网络中动态地分配货流量，以满足生产、交换和消费的需要是一个值得思考的问题。

关于物流网络的货流量分配问题，寻找最短路径进行货流量分配是决策者常用的方法。针对最短路径问题，已有大量的研究成果[1-9]。大多数学者以距离、时间、成本中某种单一属性度量路径的长度，进而研究最短路径的求解算法。如文献[6]以时间作为路径的长度单位，在考虑线路容量约束的条件下，对随机流网络的最短路径问题进行了研究。在实际情况中，我们对路径的选择不仅仅只关注时间或者距离的长短，还会考虑所耗费成本的多少等其他因素，因此，最短路径的选择应是多因素综合权衡之后的结果。有学者从多属性角度研究了最短路径问题，如文献[8]对物流运输网络多目标最短路问题进行了研究，在将多目标转化为单目标时，对每个目标的权重分配充分考虑了决策者的偏好。然而，以往的研究方法忽略了路径属性的动态性，物流网络中节点和线路的通过时间和通过成本等会随着所流经货物量的大小的不同而变化，因此对各因素属性的权衡不应固定不变。

近年来，变权理论日益受到关注，针对变权理论及其应用的研究成果不断出现[10-15]。变权理论的核心思想是：影响因素的权重随着因素状态值的变化而变化，使因素的权重能更好地体现相应因素在决策中的作用。物流网络具有复杂性和动态性特征，因此，在进行物流网络的路径选择及货流量分配时，应从动态的角度考虑多种因素的综合影响。本文在分析物流网络构成要素及要素属性之间相互关系的基础上，对这些因素由底至顶进行分层，结合决策者的因素偏好，依据变权理论，研究各层因素权重的构成与计算方法，从而建立物流网络层次变权模型，在此基础上对物流网络的货流量分配优化问题进行研究。

1 物流网络层次变权模型的构建

属性层的属性值往往以不同的物理单位进行度量，故属性值之间不具可比性。利用式(1)对属性值进行无量钢化，使关联属性具有可比性，进而可进行权重分配。

式中，Xr为r的货流分配向量，Bi(Xr)为r的属性i的属性值向量，为r在属性层（第1层）中属性i的状态值向量。并且，属性层之上的每层因素的状态值由其直接下层相关因素的状态值和变权决定，即：

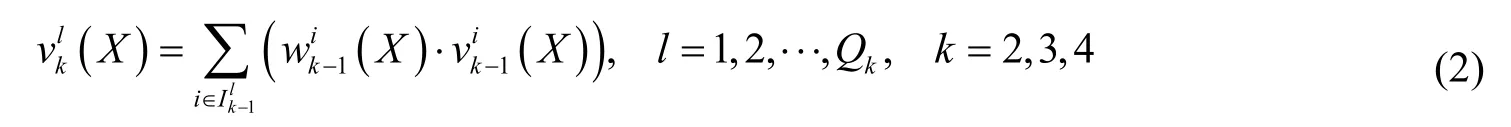
2 物流网络变权路径选择及货流分配

3 算例分析

表1 节点线路属性参数Table 1Attribute parameters of nodes and lines

3.1 属性层的状态与变权

3.1.1 节点属性状态与变权计算 供应节点、需求节点和中间节点属性值向量分别为：

由此可见，对于中间节点，其饱和度、时间和成本三个属性的权重并非固定不变，而是随着每一轮次货流量分配的变化，属性状态值会发生改变，结合决策者的偏好，各属性权重不断调整。其他各层要素的权重分配亦是如此。

3.1.2 线路属性状态与变权计算 线路属性值向量定义为：

3.2 节点线路层、子路径层和总路径层的状态与变权

根据物流网络层次变权模型，除了最底层的属性层，其余各层因素的状态值都是由直接下层中相关属性因素的状态值及变权来决定，如式(2)所示。本算例中，对节点线路层和子路经层进行评价时，我们考虑其构成属性的均衡性，故采用惩罚型状态变权函数，如式(4)所示；而对总路径层，由于在一级路径和二级路径中实施的干线运输和支线运输分别耗费的时间和成本具有较大差异，因此在进行子路经权重调整时，更侧重对一级路径的考虑，故采用如式(5)所示的激励型状态变权函数进行变权计算。

3.3 总路径选择及货流量分配

通过3.1和3.2小节的计算，最终得到物流网络中所有总路径的状态值如表2所示。

表2 总路径状态值Table 2 State values of whole paths

表3 总路径选择及货流量分配结果Table 3 Whole path selection and freight flow distribution

4 结论

在物流网络路径选择并进行货流量分配决策时，单一的常权的路径度量方式不能体现现实物流网络的动态特性。本文构建物流网络层次变权模型，研究各层因素的动态变化与决策者的决策意愿影响下的因素变权方法，以多因素的变权综合描述物流网络总路径，并在此基础上得到货流量的分配方式。该方法不仅避免了以往路径选择方法中影响因素的不可替代性，增强了决策方法的科学性，而且将决策者意愿充分体现在决策过程中，使决策方法更具实用价值。

[1]Tajdin A,Mahdavi I,Mahdavi-Amiri N,et al.Computing a fuzzy shortest path in a network with mixed fuzzy arc lengths using α-cuts[J].Computers and Mathematics with Applications,2010(4):989-1002

[2]Ioachim I,Gélinas S,Soumis F,et al.A dynamic programming algorithm for the shortest path problem with time windows and linear node costs[J].Networks,2015,31(3):193-204

[3]Santos L,Coutinho-Rodrigues J,Current JR.An improved heuristic for the capacitated arc routing problem[J].Computers&Operations Research,2009(9):2632-2637

[4]Wästlund J.Random assignment and shortest path problems[J].Dmtcs Proceedings,2015(S):1-1

[5]Wu X,Nie Y.Implementation Issues for the Reliable A Priori Shortest Path Problem[J].Transportation Research Record Journal of the Transportation Research Board,2016,2091:51-60

[6]Lin YK.Time version of the shortest path problem in a stochastic-flow network[J].Journal of Computational and Applied Mathematics,2009(1):150-157

[7]李引珍,何瑞春,郭耀煌.结点有约束的交通网络最短路径模型[J].运筹与管理,2005(4):40-43

[8]韩世莲,刘新旺,HANShi-lian,等.物流运输网络多目标最短路问题的模糊满意解[J].运筹与管理,2014(5):55-61

[9]温惠英,沈毅贤.基于层次分析法的物流配送车辆导航路径规划求权方法[J].公路交通科技,2008(8):114-118

[10]周 晓,张 锦,张 菲,等.基于变权的多目标物流网络货流分配方法[J].西南交通大学学报,2012,47(1):151-157

[11]余高锋,刘文奇,石梦婷.基于局部变权模型的企业质量信用评估[J].管理科学学报,2015(2):85-94

[12]李德清,郝飞龙.状态变权向量的变权效果[J].系统工程理论与实践,2009(6):127-131

[13]李德清,曾文艺.变权决策中均衡函数均衡效果[J].系统工程理论与实践,2016,36(3):712-718

[14]余高锋,李登峰,刘文奇.考虑决策者心理行为特征的激励型变权决策方法研究[J].系统工程理论与实践,2017,37(5):1304-1312

[15]Li DQ,Hao FL,Mathematics D.Variable weights multifactor decision making based on linguistic factor state values[J].Systems Engineering-Theory&Practice,2014,34(1):176-181