一类广义Birkhoff插值问题的适定插值基
崔 凯
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
一类广义Birkhoff插值问题的适定插值基
崔 凯
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
Birkhoff插值在应用密码学,逼近论以及PDE求解等领域有着重要应用。由于微商插值条件的不连续性,使得该问题比Lagrange和Hermite插值要复杂的多。提出了基于多项式微分条件的广义Birkhoff 插值格式。探究广义Birkhoff插值问题的适定插值基,使得对任意给定的型值,在该组基张成的空间中插值时总存在唯一满足插值条件的多项式。采用代数几何的方法,通过对多样性的插值条件分析,证明了当定义插值格式的关联矩阵满足较好的性质时,适定的插值基无需繁琐的计算,可以由微分插值条件直接获得。最后通过算例验证了该方法的有效性。
Birkhoff插值; 适定插值基; 关联矩阵; 正则链
0 引 言
继Newton, Lagrange和Hermite之后,Birkhoff[1]于1906年提出了微商条件不连续的插值问题,即Birkhoff插值。1966年Schoenberg[2]首次给出了经典的一元Birkhoff插值格式,由关联矩阵,插值结点集和插值空间3部分组成,并提出插值问题的可解性可由关联矩阵的性质刻画。Lorentz等[3]于1992年在其专著中将Schoenberg提出的一元Birkhoff插值格式推广到了单项微分插值条件的多元情形,并且给出了插值格式正则性的若干判定条件。此后的20多年,一方面,一些学者对具有不同特征的插值格式进行研究,得到了关于Birkhoff插值正则性的若干判定结论[4-8];另一方面,一些学者根据给定的插值结点集和插值条件,寻找合适的插值基。Wang等[9]针对插值条件为连通集的情形构造了插值问题的Newton基。Lei基于MB算法[10],提出了计算量较低的B-MB算法[11]求解多元Birkhoff插值问题字典序下的极小单项基。考虑结点集的摄动情形,Cui等修正了SOI算法[12],提出了计算多项式微分条件下的Birkhoff插值问题的稳定单项基算法[13]。2016年,Zheng等[14]研究了单项微分插值条件下的唯一极小单项基问题。
本文将Lorentz的多元Birkhoff插值格式推广到了多项式微分插值条件的情形,证明了一类具有较好性质的插值问题可以直接由插值条件得到其适定的插值基。
1 广义Birkhoff插值格式

αi1+αi2+…+αin<αj1+αj2+…+αjn;
αi1+αi2+…+αin=αj1+αj2+…+αjnαi1=αj1,…,αim=αjm,且αi(m+1)<αj(m+1)。
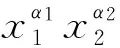
定义3 广义Birkhoff插值格式包含3个部分:

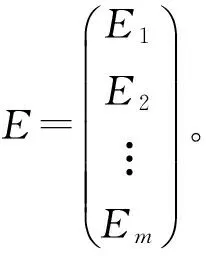

定义4 给定广义Birkhoff插值格式(S,Z,E),与之对应的插值问题可以描述为求一组插值基,使得对任意给定的一组实数cij,在该组基张成的空间中都存在唯一的多项式f满足插值条件:
这样的插值基称之为适定的插值基。
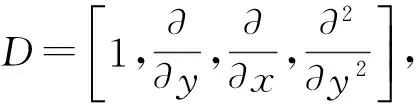
2 主要结果
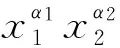
注:乘积序不是单项序,因为并不是任意2个单项都可以在乘积序下比较大小,比如根据定义5,既不能得到x2y3>x3y2,也不能得到x3y2>x2y3,此时称这2个单项在乘积序下是不可比较大小的。若ti>tj或ti与tj不可比较,则称ti不小于tj.
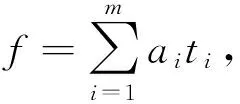
定义6 设S是按分次字典序排列的单项序列,称[S1,S2,…,Sm]为序列S的正则链,若满足
1)Si⊂S,i=1,…,m;
2) 子序列Si中的单项在乘积序下是不可比较大小的,i=1,…,m;

1) 关联矩阵的每一列中至多有一个非零元素;


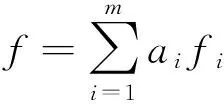
例2 给定广义Birkhoff插值格式(S,Z,E),S=[1,y,x,y2,xy,x2,y3],Z={(x1,y1),(x2,y2),(x3,y3)}。关联矩阵
显然关联矩阵的每1列至多有1个非零元素,符合定理中的第1个条件。以下检验定理中的第2个条件。
1)S1=[1]⊂S,S2=[xy,y3]⊂S,S3=[y,x2]⊂S;
2) 在乘积序下,S2中的单项xy和y3不能比较大小,S3中的单项y和x2也不能比较大小;
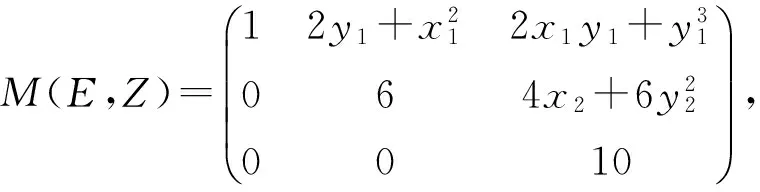
3 结 论
本文刻画了一类具有较好性质的广义Birkhoff插值问题,与其他计算适定插值基的算法不同,本文证明了该类问题的适定多项式基无需计算,可由给定的插值格式直接获得。算例表明,定理提供的方法在解决特定的一类广义Birkhoff插值问题时具有一定的优越性。
[ 1 ]BIRKHOFF G D. General mean value and remainder theorems with applications to differentiation and quadra-ture[J]. Trans Amer Math Soc, 1906,7(1):107-136.
[ 2 ]SCHOENBERG I J. On Hermite-Birkhoff interpolation[J]. J Math Anal Appl, 1966,16:538-543.
[ 3 ]LORENTZ R A. Multivariate Birkhoff interpolation[M]. Berlin: Springer Verlag, 1992:1-192.
[ 4 ]PALACIOS F,RUBIO P. Generalized Pólya condition for Birkhoff interpolation with lacunary polynomials[J]. Appl Math E-Notes, 2003,3:124-129.
[ 5 ]CRAINIC N. Necessary and sufficient conditions for almost regularity of uniform Birkhoff interpolation sche-mes[J]. Acta Univ Apulensis Math Inform, 2003,5:61-66.
[ 6 ]CRAINIC N. UR Birkhoff interpolation with rectangular sets of derivatives[J]. Comment Math Univ Carolin, 2004,45(4):583-590.
[ 7 ]CRAINIC N. UR Birkhoff interpolation schemes: reduction criterias[J]. J Numer Math, 2005,13(3):197-203.
[ 8 ]CRAINIC M, CRAINIC N. Birkhoff interpolation with rectangular sets of nodes and with few derivatives[J]. East J Approx, 2008,14:423-437.
[ 9 ]WANG Xiaoying, ZHANG Shugong, DONG Tian. Newton basis for multivariate Birkhoff interpolation[J]. J Comput Appl Math, 2009,228(1):466-479.
[10]CERLIENCO L, MUREDDU M. From algebraic sets to monomial linear bases by means of Combinatorial algorithms[J]. Discrete Math, 1995,139(1):73-87.
[11]LEI Na, CHAI Junjie, XIA Peng, et al. A fast algorithm for multivariate Birkhoff interpolation problem[J]. J Comput Appl Math, 2011,236(6):1656-1666.
[12]ABBOTT J, FASSINO C, TORRENTE M L. Stable border bases for ideals of points[J]. J Symbolic Comput, 2008,43(12):883-894.
[13]CUI Kai, LEI Na. Stable monomial basis for multivariate Birkhoff interpolation problems[J]. J Comput Appl Math, 2015,277:162-170.
[14]ZHENG Xiaopeng, CHAI Juejie, SHENG Mengci. On the unique minimal monomial basis of Birkhoff interp-olation problem[J]. J Syst Sci Complex, 2016,29(3):825-841.
[15]张树功,雷娜,刘停战. 计算机代数基础[M]. 北京:科学出版社, 2005:1-222.
[16]COX D A,LITTLE J,O’SHEA D. Ideals,varieties,and algorithms[M]. New York: Spriner-Verlag, 1997:1-541.
ProperinterpolationbasisforaclassofgeneralizedBirkhoffinterpolationproblems
CUIKai
(College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)
Birkhoff interpolation has significant applications in the fields of applied cryptography, approximation theory and PDE theory, etc. The noncontinuity of derivative conditions makes Birkhoff interpolation to be more complicated than Lagrange and Hermite interpolation. A generalized Birkhoff interpolation scheme based on polynomial differential conditions is proposed. Proper interpolation basis of the generalized Birkhoff interpolation problem is studied and a unique polynomial which satisfies interpolation conditions always exists in the space spanned by the basis for any given data values. Applying the method of algebraic geometry to analyze various interpolation conditions, we prove that when the interpolation scheme defined by incidence matrix satisfies some good properties, the proper interpolation basis can be directly obtained from differential interpolation conditions, instead of tedious computations. Finally, an example is given to illustrate the effectiveness of the proposed method.
Birkhoff interpolation; proper interpolation basis; incidence matrix; regular chain
2017-06-05。
辽宁省科技厅自然科学基金资助项目(20170540821)。
崔 凯(1986-),男,吉林辽源人,沈阳师范大学讲师,博士。
1673-5862(2017)04-0441-04
O241.3
A
10.3969/ j.issn.1673-5862.2017.04.012

