基于粒子群算法的分布式能源系统容量优化配置

杨佳霖

(中国大唐集团科学技术研究院有限公司，北京 石景山 100040)

基于粒子群算法的分布式能源系统容量优化配置

杨佳霖

(中国大唐集团科学技术研究院有限公司，北京 石景山 100040)

系统容量配置问题是影响分布式能源项目盈利能力的关键，为此提出了以储热设备取代部分动力设备容量的分布式能源系统方案，将系统的物理模型和运行策略进行数学模型转化，针对具体电、热负荷情况，采用粒子群优化算法，以净现值最大为目标，对动力设备容量和储热设备容量进行优化求解，并采用遍历法对结果进行验证。分析结果表明：最优的动力设备容量小于最大电负荷，在电负荷峰期存在网购电量，但机组绝大多数时间运行于额定工况或微偏离额定工况，机组发电效率相对较高；由于天然气价格高，补燃天然气不经济，最优的储热容量配置为在严寒期内不以补燃形式对供热能力进行补充，仅利用储热设备恰好能够满足严寒期的供热需求，即不存在储热设备的配置冗余。

分布式能源；粒子群算法；容量配置优化；内燃机；储热

0 引言

“十三五”规划纲要指出“要深入推进能源革命，着力推动能源生产利用方式变革，优化能源供给结构，提高能源利用效率，建设清洁低碳、安全高效的现代能源体系，维护国家能源安全”。《能源发展战略行动计划(2014—2020年)》也指出要“坚持节约、清洁、安全的战略方针，加快构建清洁、高效、安全、可持续的现代能源体系”。分布式能源是实现上述国家能源规划的一项重要技术手段。分布式能源是分布在用户端的能源综合利用系统，因其以能量梯级利用为用能原则，在需求端直接对能源进行生产和消纳，能源供应可靠灵活且能源综合利用效率高，同时，分散排放使其对环境的负面影响减小[1]。分布式能源系统是能源互联网中的必要环节，也是未来世界能源技术的重要发展方向[2]。

我国分布式能源起步较晚，核心设备制造技术和运行维护技术仍然不够成熟[3]，加之天然气价格波动，尽管国家对分布式能源给予一定的补贴和税率优惠，但当前上马的诸多项目仍然难以盈利、甚至亏损严重。分布式能源系统容量配置问题是影响分布式能源项目盈利能力的关键问题之一[4]，无论项目采用“以电定热(冷)”还是“以热(冷)定电”运行，若能源动力设备按照满足最大电或热(冷)负荷进行设计，因电或热(冷)负荷均具有波动特性，动力设备必然不能长时间运行于额定负荷或微偏额定负荷工况，动力设备存在严重容量冗余，初期成本增大，后期运行小时数偏低；若设备容量仅以满足最低负荷配置，无论初寒(暑)期、末寒(暑)期、机组能够满负荷运行，但动力设备容量配置偏低会造成补燃调峰锅炉的容量配置偏高，补燃天然气供暖(制冷)的经济性更差，因此需要调整分布式能源供能方式且规划最优的容量配置方案使得系统经济性达到最佳。

本文针对该问题，提出一种利用粒子群优化算法优化配置分布式能源系统动力设备容量的方法，以北方公用建筑采暖热负荷为计算基础，利用储热设备取代部分动力设备容量，满足热负荷峰期调配的技术方案，将燃机满足供热负荷后多余热量及谷期电能通过热泵技术制取热量储存，满足热负荷高峰需求，以净现值最大为目标函数，计算最优动力设备和储热设备配置容量。

1 粒子群算法在分布式能源系统容量配置中的应用

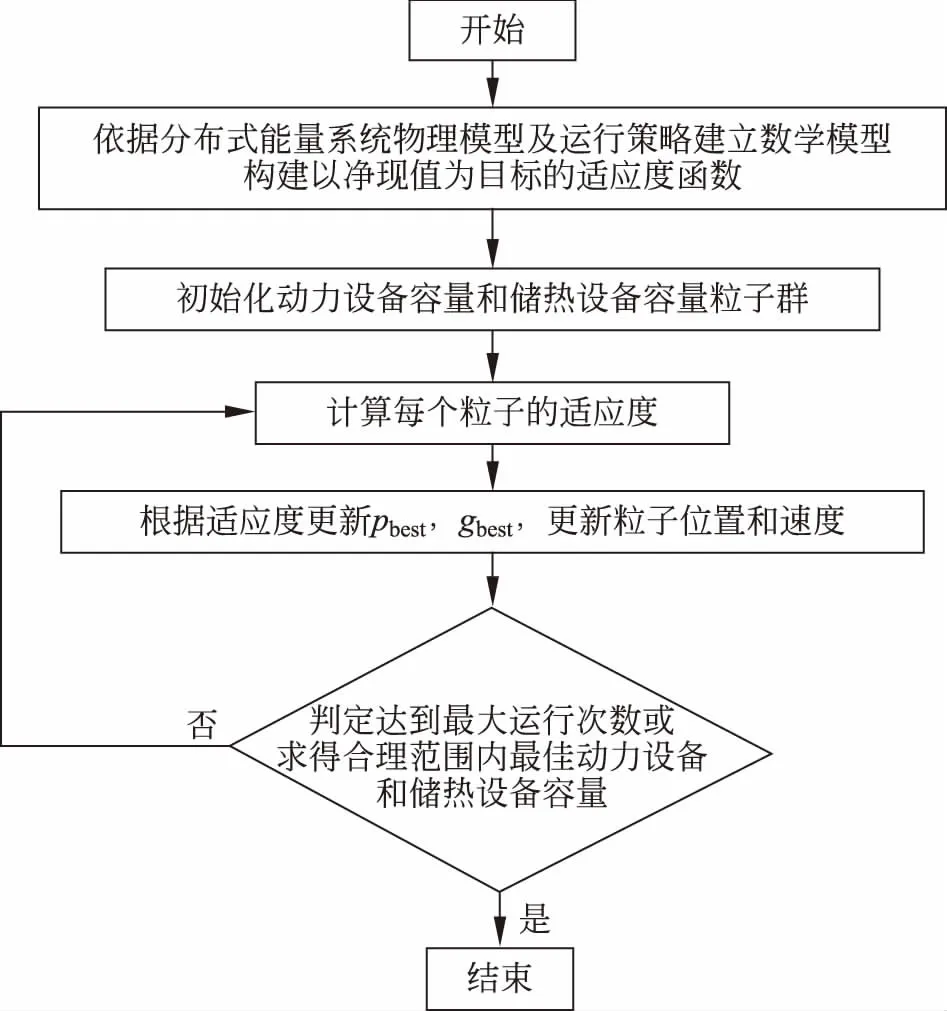
图1 PSO算法优化分布式能源系统容量配置流程图Fig.1 Optimization allocation process of DES based on particle swarm optimization algorithm

粒子群优化算法(particle swarm optimization, PSO)是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法，是群集智能的一种。PSO算法计算原理较为成熟，这里不做详述，具体可参考文献[5-8]。本文主要以项目净现值为目标函数，利用PSO算法对分布式能源系统动力设备和储热设备的容量进行优化求解。PSO算法优化分布式能源系统容量配置的流程如图1所示。首先，依据分布式能量系统物理模型及运行策略建立数学模型，构建以净现值为目标的适应度函数。而后，在合理区间内随机初始化以动力设备容量和储热设备容量为位置坐标的粒子群，计算粒子群内每个粒子的适应度，根据适应度结果粒子更新自身经历的最优位置pbest，粒子群更新粒子群的最优位置gbest。同时，粒子根据最优位置与当前位置的关系，更新粒子速度及下一次计算的粒子位置，直至判定达到最大运行次数或求得合理范围内最佳的粒子位置，即最优的动力设备和储热设备容量。该算法关键在于更新粒子位置时，考虑了粒子先前速度、粒子“自身认知”部分(粒子当前位置与自身经历过最好位置的距离)和粒子“社会认知”部分(粒子当前位置与群体经历过最好位置的距离)，因此具有精度高、收敛快的优点，常被应用于解决实际问题。

2 分布式能源系统容量配置实例分析

2.1 负荷情况

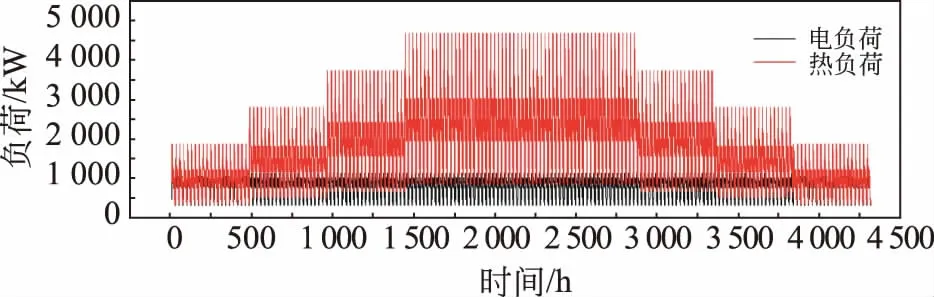
图2 采暖期电、热负荷情况Fig.2 Heating and power load in heating period

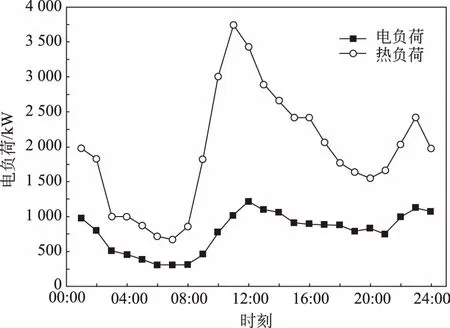
图3 典型日逐时电、热负荷曲线Fig.3 Hourly power and heating load of typical day

以最简单的北方某公共楼宇电、热负荷为例，具体负荷情况及典型日逐时电、热负荷情况如图2，3所示。可以看到：全年共有6个月的采暖期，电负荷在该周期内运行相对平稳，而采暖负荷具有明显的初寒期、严寒期、末寒期波动特征，初寒期和末寒期分3个阶段，越接近严寒期，热负荷值越高；同时，电、热负荷每天逐时需求也随着人类活动存在周期性波动，午夜过后电、热负荷较低，白天电、热负荷相对较高，且电、热负荷在波动周期上具有一定的同步性。

2.2 物理模型及运行策略

文献调研显示，兆瓦级或小于兆瓦级分布式能源项目一般采用燃气内燃机作为动力设备，因其在该容量级别具有较高的发电效率和相对低廉的设备价格[9]。根据主动力设备情况及负荷状况建立该系统的物理模型如图4所示。空气与天然气在内燃机气缸中燃烧，膨胀推动内燃机曲轴转动，曲轴通过调速装置拖动发电机转动发出频率和电压稳定的电能。内燃机可被利用的余热是高温烟气和缸套冷却水，缸套冷却水出口温度为90～100 ℃，被用于高效换热器低温段加热；烟气温度一般在400 ℃以上，用于高效换热器高温段加热，加热后热网水输送至热用户满足采暖热负荷需求。以储热设备作为调峰装置，利用燃气内燃机多余热量及电价谷期电能制取热量储存。燃气锅炉也可通过直接燃烧天然气方式获取热量，满足热负荷需求。

图4 燃气内燃机分布式能源系统Fig.4 Distributed energy system driven by gas turbine

采用并网不上网的运行方式，即分布式能源系统可以从电网取电，但不向电网输电，电网可作为分布式能源系统备用，也可在区域用电负荷高峰时，提供稳定电力来源。热负荷方面，根据供热能耗高低[10]，优先利用燃气内燃机烟气及缸套水余热，不足时，由蓄热设备提供，再不足时以补燃天然气形式满足。蓄热设备中的热量来自于多余的烟气余热及电价谷期取自电网的电能，这里电能以压缩式热泵的方式制取，并设定在电价谷期时段，电动压缩式制冷机组额定工况运行能够充满整个蓄热罐。

2.3 数学模型及净现值函数

参考秦渊等[11]依据颜巴赫624型机组拟合的燃气内燃机发电功率与排烟参数和缸套水温度、流量等无量纲参数的性能关系，具体模型的数学表达式为：

设定在电价谷期时段，电动压缩式制冷机组额定工况运行能够充满整个蓄热罐，则热泵的额定功率EHP与蓄热容量QTES存在线性关系，因此只需对二者之一进行优化求解即可获得另外参数的配置容量。蓄热罐储热量与热泵额定功率的关系式为

QTES=EHPCHPΔt

(7)

式中：CHP为电动热泵机组制热系数；Δt为电价谷期时间。

基于以上数学模型及供能策略判定关系，即可逐时计算该小时内燃料消耗量、网购电量、供热量、发电量等机组运行参数，参考当前燃料、电价及热价即可建立该小时内成本与收益状况。由于项目采用并网不上网，完全自发自用的形式，这里的收益表现为分布式能源系统运行后与原供能方式的用能成本差额。对整个运行周期的成本、收益进行累积，扣除期间内运维费用即为该供暖周期内的现金流量，于是可构建净现值与机组容量和热泵机组容量的适应函数，如下

(8)

式中：ΔCt为第t年净现金流量，主要涵盖初投资、燃料成本、购电成本、运营成本、电、热收益，残值等；i0为基准折现率(基准收益率)；n为项目计算寿命期。

2.4 优化结果及分析

通过粒子群优化算法获得的具体容量配置及优化计算结果(不考虑真实设备型号，仅以计算为准)如表1所示。

表1 容量配置及计算结果Table 1 Allocation of system and computational results

注：电动压缩式热泵制热系数为3.0；天然气价格为3.0元/m3；峰期(06:00—22:00)电价为1.2元/(kW·h)，谷期(22:00—次日06:00)电价为0.4元/(kW·h)；供热价格取45 元/GJ；运营费用取50元/(MW·h)；燃气机组单位造价取9 000元/kW；补燃锅炉单位造价取500元/kW；电动压缩式热泵单位造价取1 000元/kW；蓄热设备单位造价500元/m3；天然气发电行业的基准折现率9%，项目寿命期为20年，残值系数取0.1。

由表1可以看到，优化配置的机组发电功率小于最大电负荷所需功率，即在机组工作过程中存在机组供电能力不足，该时间段需从电网购买峰期电量，购电电量为23.09万 kW·h。获得如此结果主要是因为：(1)通过降低机组容量能够减少机组初始投资；(2)电负荷为波动负荷，机组配置容量小，可以较长时间运行于额定负荷或微偏离额定负荷，机组发电效率高，综合比较以牺牲较小的购买峰期电量投入获得更佳的运行工况并降低初期成本，获得最大的经济效益。由于热负荷大于电负荷，而燃气内燃机组的热电比约为1，因此仅在初寒期和末寒期存在供热能力大于热负荷状况，即机组供热余量储存量较小为7.97 GJ，若热电负荷状况与机组热电比相适应，且用电峰谷差异与用热峰谷不同步时，蓄热设备的“削峰填谷”作用将体现的更为明显。优化结果显示，机组供热量不足时，完全以蓄热设备进行补充，补燃锅炉并未运行，说明直接燃用天然气进行供热在经济上较为不合理，要差于利用谷期电能通过热泵进行供暖的经济性，因此在以净现值为优化目标函数时，程序并未选择采用补燃形式对供热能力进行补充。净现值大于0，说明优化配置系统能够实现9%的天然气发电行业的基准收益率，项目具有可行性。

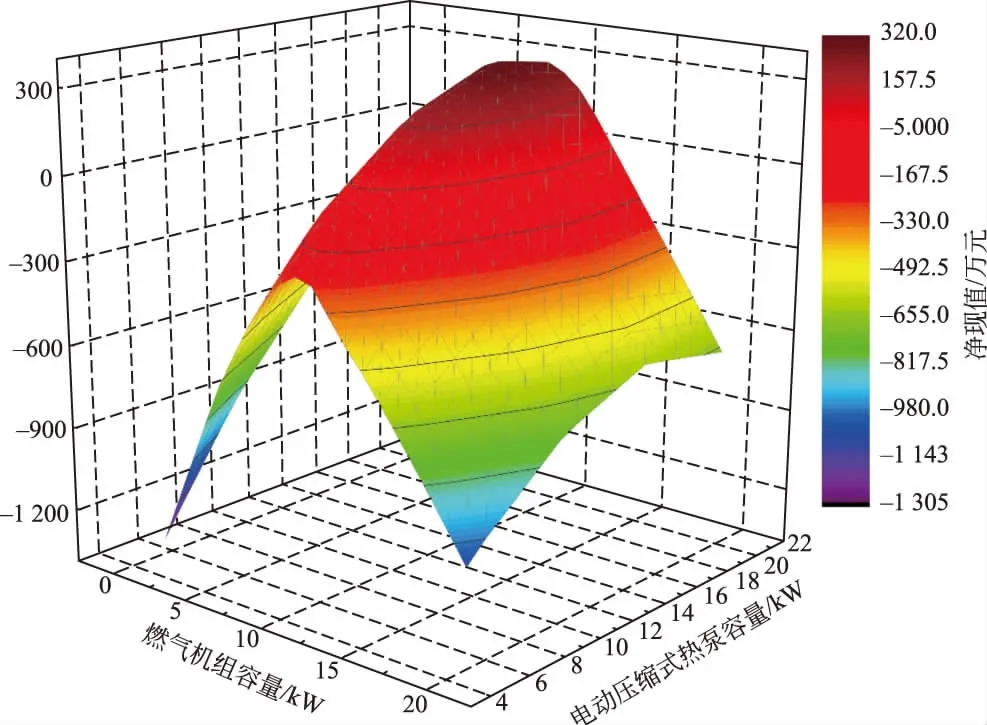
图5 采用遍历法对优化结果的验证Fig.5 Optimization result validation by traversing method

图5为采用遍历法对优化结果的验证，这里选取优化容量两侧一定范围内的数值，计算不同容量配置条件下的项目净现值，结果显示燃气内燃机容量为[9,10]，电动压缩式热泵容量在[16,18]区间内取得最优值，与优化结果吻合。该图也表明：(1)燃气机组容量的变化对净现值的影响较为显著，当燃气机组容量配置较低时，需要从电网购入大量的峰期电量，满足电负荷需求，而峰期电价昂贵，直接影响项目经济性；(2)在蓄热设备容量一定的条件下，降低燃气机组容量配置后，燃气机组和蓄热设备的整体供热能力不足以满足热负荷需求，此时补燃锅炉运行，天然气直接燃烧供热造成经济性下降；(3)当燃气机组配置容量过高时，机组不能长时间运行于额定工况或微偏离额定工况，造成发电效率降低，此外，容量配置冗余也会造成初投资增大，净现值下降。

图6 蓄热设备储热量在整个供暖期内运行曲线Fig.6 Operation curve of thermal energy storage device during heating period

图6为蓄热设备储热量在整个供暖期内运行曲线，在初寒期和末寒期由于热负荷较小，储热设备中储存的热量并不能完全被利用，以24 h为一个运行周期进行分析，在谷期电价结束时储热设备均可达到最大储热量。进入严寒期，热负荷增大，储热设备放热量增大且大于储热设备在电价谷期储存的热量，因此在电价谷期结束时，储热设备中储存的热量不能达到最大值，随着严寒期的延续，每天电价谷期结束时储存在储热设备的热量不断下降，直至储热设备储热量降至零，此时严寒期结束。而后，进入末寒期，热负荷降低，储热设备放热量减小，在电价谷期结束时能够将储热量储存至最大值。由于在严寒期结束时，蓄热设备储热量降低至零，因此系统无需补然设备即可满足热负荷需求。

图7为初寒期到严寒期典型日蓄热设备运行情况，可以看到随着热负荷的增大，储热设备供热量逐渐增大，电价谷期由电动压缩式热泵制取热量也逐渐增大，直至进入严寒期电动热泵制取热量不能完全将储热设备充满。

图7 初寒期到严寒期典型日蓄热设备运行情况Fig.7 Operation state of thermal energy storage device on typical days from initial cold period to freeze-up

图8为初寒期到严寒期典型日逐时供热运行图，可以看到在初寒期，热负荷最小阶段，燃机在满足供热负荷后仍有剩余。若此时储热设备储热未满，该部分多余热量可被储存到储热设备中；若此时处于谷期电价阶段，且电动压缩式热泵已将储热设备热量储满时，该部分多余热量则被排放到环境中。该部分余热热量较小，进入初寒期第二阶段后，由于热负荷增大，且蓄热设备放热量增大，已不存在过量余热被储存和浪费的部分。由初寒期到严寒期燃机供热量相对较为平稳，大部分时间运行于额定工况或微偏离额定工况，满足供热基础负荷需求，储热设备利用用电谷期相对较为经济的电量制取热能满足供热尖峰时段的需求，且随着热负荷增大，储热设备在供热负荷占比中逐渐增大。

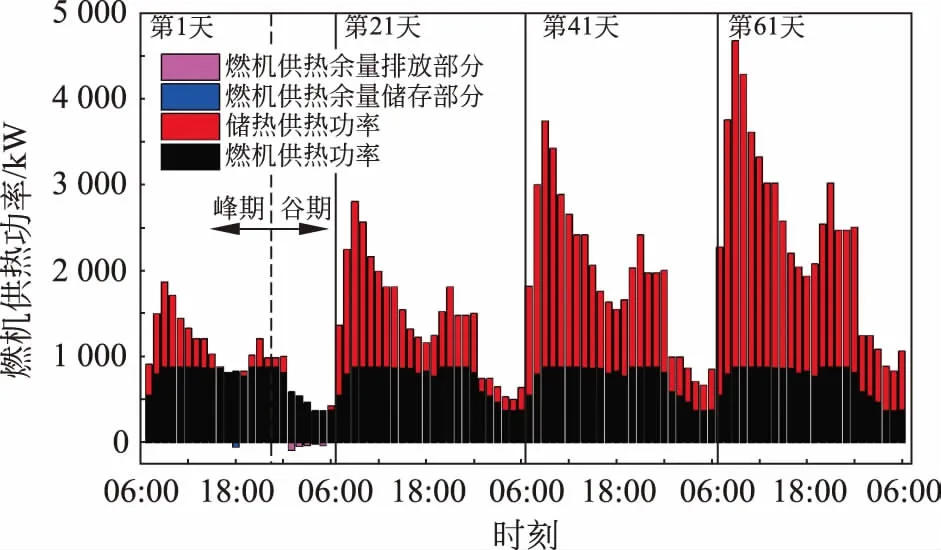
图8 初寒期到严寒期典型日逐时供热设备运行状态Fig.8 Operation state of heating device on typical days from initial cold period to freeze-up

3 结论

(1) 以粒子群优化算法能够求得分布式能源系统最优容量配置，计算速度快且结果准确性较高。

(2) 以储热设备取代部分动力设备容量的方式能够实现较好的供能灵活性和可靠性，由于储热设备价格低于动力设备价格，若容量配置合理可获得较好的经济效益。

(3) 针对所提分布式能源系统，由于电、热负荷的波动性，最优的动力设备容量小于最大电负荷，在电负荷峰期存在网购电量，但机组绝大多数时间运行于额定工况或微偏离额定工况，机组发电效率高，综合经济效益好。

(4) 由于燃气价格高，补燃天然气不经济，最优的储热容量配置为在严寒期内不进行补燃而仅以储热的形式对热负荷进行补充，且恰好在严寒结束时，储热设备储热量归零，即不存在储热设备的配置冗余。

[1] 李立浧, 张勇军, 徐敏. 我国能源系统形态演变及分布式能源发展[J]. 分布式能源, 2017, 2(1): 1-9.

LI Licheng, ZHANG Yongjun, XU Min. Morphological evolution of energy system and development of distributed energy in China[J]. Distributed Energy, 2017, 2(1): 1-9.

[2] 冯江华, 陈晓丽. 能源体制改革开创能源互联网时代[J]. 南方能源建设, 2015(3): 10-16.

FENG Jianghua, CHEN Xiaoli.Energy system reform creates energy internet era[J]. Southern Energy Construction, 2015, 2(3): 10-16.

[3] 谈孜超. 分布式冷热电三联供系统集成优化研究[D]. 天津： 天津大学, 2012.

TAN Zichao. Integrated optimization research on distributed cooling heating and power system[D]. Tianjin： Tianjin University, 2012.

[4] 叶彩花, 白一, 乔丽洁. 燃气冷热电联供分布式能源系统中发电机组选择的分析探讨[J]. 城市燃气, 2014(2): 21-24.

YE Caihua, BAI Yi, QIAO Lijie. Research on optimum selection of power equipment in distributed energy system combined cooling heating and power[J]. Chengshi Ranqi, 2014(2): 21-24.

[5] 刘波. 粒子群优化算法及其工程应用[M]. 北京： 电子工业出版社, 2010.

[6] 王大志. 面向实际工程问题的粒子群优化算法应用技术的研究[D]. 沈阳： 东北大学, 2009.

WANG Dazhi. Research on applications of particle swarm optimization to industry engineering problems[D]. Shenyang： Northeastern University, 2009.

[7] 王智冬, 刘连光, 刘自发, 等. 基于量子粒子群算法的风火打捆容量及直流落点优化配置[J]. 中国电机工程学报, 2014, 34(13): 2055-2062.

WANG Zhidong, LIU Lianguang, LIU Zifa, et al. Optimal configuration of wind & coal power capacity and DC placement based on quantum PSO algorithm[J]. Proceedings of the CSEE, 2014, 34(13): 2055-2062.

[8] 杨珺, 张建成, 黄磊磊,等. 基于改进粒子群算法的独立光伏发电系统储能容量优化配置研究[J]. 华东电力, 2012(8):1370-1374.

YANG Jun, ZHANG Jiancheng, Huang Leilei, et al. Energy storage capacity optimization for independent PV power system based on improved PSO algorithm[J]. East China Electric Power, 2012(8): 1370-1374.

[9] 左政, 华贲. 燃气内燃机与燃气轮机冷热电联产系统的比较[J]. 煤气与热力, 2005, 25(1): 39-42.

ZUO Zheng, HUA Ben. Comparison between gas engine and gas turbine CCHP systems[J]. Gas & Heat, 2005, 25(1): 39-42.

[10] 李沛峰, 戈志华, 银正一, 等. 供热系统能耗评价模型及应用[J]. 中国电机工程学报, 2013, 33(23): 19-28.

LI Peifeng, GE Zhihua, YIN Zhengyi, et al. Model for energy consumption of heating system and its application[J]. Proceedings of the CSEE, 2013, 33(23): 19-28.

[11] 秦渊, 杨洁, 吕春杰. 基于颜巴赫燃气内燃机的分布式能源系统变工况特性研究[J]. 发电与空调, 2014, 35(2): 1-3.

QIN Yuan, YANG Jie, LV Chunjie. Analysis of the off-design performance of DES based on JMS gas engine[J]. Power Generation & Air Condition, 2014, 35(2): 1-3.

OptimizationAllocationofDistributedEnergySystemBasedonParticleSwarmOptimizationAlgorithm

YANG Jialin

(China Datang Corporation Science and Technological Research Institute Co., Ltd., Shijingshan District, Beijing 100040, China)

Capacity allocation problem is one of key factor to influence the profitability of distributed energy system (DES) projects. This paper proposes a DES solutions that uses heat storage equipment to replace part of power equipments to reduce the capacity. The physical model and operation strategy of this system are transformed into mathematic model. A special heat and electricity loads are used as the calculation basis and the particle swarm optimization (PSO) is applied to calculate the capacities of power equipment and heat storage equipment with the maximum net present value as the goal. The result is validated by traversing method. It shows that the optimal capacity of power equipment is less than the maximum electricity load, and the system need to purchase electricity from power grid during the peak period of electrical load. However, most of time, the power unit has higher efficiency, because it works in rated condition or close to rated condition. The natural gas is expensive and it is uneconomical to burn gas for peak heating load. The optimal heat storage capacity configuration is to supplement the heating capacity in the cold period without gas combustion, only use heat storage equipment to meet the heating load demand exactly in freeze-up. That is, there is no configuration redundancy for heat storage equipment.

distributed energy; particle swarm optimization algorithm; optimization allocation; internal-combustion engine; thermal energy storage

TK 01

A

2096-2185(2017)06-0046-06

10.16513/j.cnki.10-1427/tk.2017.06.008

杨佳霖

杨佳霖(1986—)，男，工学博士，工程师，研究方向为分布式能源系统集成及火力发电厂节能优化，yangjialin@cdt-kxjs.com。

2017-08-16

(编辑 蒋毅恒)