核自旋与乙烯分子的核自旋变体的分离和转换研究进展

孙振东，马丽莎

山东大学物理学院，济南，250100；喀什大学物理与电气工程学院，喀什，844006

核自旋与乙烯分子的核自旋变体的分离和转换研究进展

孙振东∗，马丽莎

山东大学物理学院，济南，250100；喀什大学物理与电气工程学院，喀什，844006

原子核（简称核）由质子和中子构成，核内所有质子和中子的角动量之和通常称为核自旋。虽然核自旋变体及其稳定性是量子力学中的基本概念，而且由核自旋不为零的同种原子组成的所有分子都有两种或两种以上的核自旋变体，但对气相多原子分子核自旋变体的分离和相互转换动力学的研究，直到九十年代初才打破了沉寂了几十年的局面。十多年前乙烯分子的四种核自旋变体的分离和转换实验研究有了首次突破，本文对此做了重点介绍。文章按年代发展首先简要地综述了构成原子核的质子和中子发现的科学史，提出了核自旋变体的概念，详细描述了氢分子的两种核自旋变体（正氢和仲氢）以及乙烯分子的四种核自旋变体。然后着重介绍了利用光诱导漂移技术，对气相乙烯分子的核自旋变体的分离实验；用宇称守恒与量子弛豫理论定量地描述了核自旋变体间相互转换研究的进展。最后概述了通过仲氢对乙炔催化加氢的化学合成方法用来提高乙烯分子的核自旋变体浓度，足以增强其核磁共振信号强度的最新成果。

质子；中子；核的构成；核自旋变体；分离和转换率；光诱导漂移；量子弛豫；宇称守恒；乙烯；精密激光光谱；核磁共振

目 录

I.引言193

II.原子核的组成与核自旋 194

A.核放射性衰变的三种放射线及其实质 194

B.核的构成和质子的发现 194

C.中子的发现 196

D.原子核是由质子和中子组成的 199

E.核自旋与核自旋磁矩 201

III.核自旋变体与氢分子和乙烯分子的核自旋变体 201

A.核自旋变体与氢分子的两种核自旋变体 201

B.乙烯分子的四种核自旋变体 202

IV.乙烯分子的核自旋变体的分离及其相互转换 203

A.乙烯分子的核自旋变体的分离及其相互转换研究的实验方案和实验装置 203

B.光诱导B2u核自旋变体分离的实验观测结果和分析 204

C.乙烯分子四种核自旋变体转换中的宇称守恒及其核自旋变体间的转换观测结果与分析 206

V.总结和展望 208

致 谢 209

210

I.引言

事物的核心是其最关键的组成部分，是决定事物本质特性的最主要部分。原子是合成分子和物质的基本单元，是由原子核和电子组成的，而原子核是原子的核心，所以，原子核对原子与分子和物质的物理性质起决定性的作用。再加上自旋是微观粒子的內禀属性，原子核自旋和原子核自旋磁矩等相关物理量的研究对原子核构成及其构成成分等根本问题的解决在历史上都起了巨大的作用，而且直到现在一直是物理学进展中的重要研究课题之一。然而，对于由原子核（简称核）自旋量子化状态的不同而构成的新分子及其物理性质的研究，直到目前还仍处于探索的起步阶段。为达到抛砖引玉的目的，本文对核自旋与核自旋变体，以及气相分子的核自旋变体的分离和转换研究进展进行了综述。

核自旋变体(nuclear spin isomers)是指因分子中对称位置上的同种原子的核自旋状态的不同而引变出的新分子。由核自旋不为零的同种原子组成的所有分子都有两种或两种以上的核自旋变体，它们分别对应一定的总核自旋Iħ。原子核是由质子和中子构成的，核自旋就是核内所有质子和中子的角动量之和。本文首先按年代发展详细地概述了构成原子核的质子和中子发现的科学史，提出了核自旋变体的概念，描述了氢分子的两种核自旋变体–正氢与仲氢，以及乙烯分子的四种核自旋变体，然后着重全面地介绍了利用光诱导漂移技术对气相乙烯分子的四种核自旋变体的分离和转换研究的进展，及其相关应用和研究的最新成果。

II.原子核的组成与核自旋

A.核放射性衰变的三种放射线及其实质

1895年，卢瑟福(E.Rutherford)由新西兰来到英国剑桥大学卡文迪许实验室成为电子发现者汤姆逊(J.J.Thomson)的第一个留学生。1896年。当他得知贝克勒尔(A.H.Becquerel)发现了铀(U)有放射性现象后[1,2]，他与他的助手和学生们便开始研究放射性物质，以及用其作辐射源探索原子的结构和原子核的组成，从此获得了许多具有划时代意义的物理发现和与本文相关的重要研究成果。1898年，皮埃尔–居里夫妇(Pierre-Curie)在法国[3]和卢瑟福在加拿大[4,5]相继发现天然放射性元素钍 (Th)、钋 (Po)、镭 (Ra)[6]。1899年，卢瑟福发现铀和铀的化合物所发出的射线有两种不同类型：极易被物质吸收的α-射线和穿透力较强的的β-射线[7]。1900年，维拉德(P.U.Villard)将镭盐（氯化镭,RaCl2）发出的辐射穿过薄铅箔时发现了除α-射线和β-射线外的另一种穿透力更强的电磁波辐射[8,9]，后来卢瑟福称其为γ-射线[10]。这是因为当原子核放射出α-射线或β-射线时，产生的新原子核往往处于其激发态能级。而处于激发态的原子核是不稳定的，所以当它向较低能态跃迁时就产生了向外辐射的电磁波γ-射线。由于原子核的能级间隔比原子能级间隔大得多，因此原子核辐射的γ-射线是频率很高的电磁波，而且它往往伴随着α-射线或β-射线的产生。贝克勒尔指出β-射线是阴极射线高速电子流[1,11]。1902年卢瑟福与索迪(F.Soddy)提出了革命性的元素蜕变假说[12]:放射性是由于原子本身分裂或蜕变为另一种元素的原子而引起的。1903年他们与拉姆齐(W.Ramsay)共同合作，揭示了α-射线的本质是带正电荷的氦离子流[13]。卢瑟福和索迪分别获得了 1908年和1921年的诺贝尔化学奖。利用磁谱仪，通过测量出粒子运动轨迹的曲率半径求得的粒子动能，可得到组成射线的粒子数即射线强度随粒子动能的变化关系图（能谱图）。α-粒子的分立能谱实验结果说明原子核这个量子体系的能量及其释放的能量是不连续的。但对与α-射线同时被卢瑟福发现的β-射线，1914年在柏林的盖革(H.Geiger)实验室，查德威克(J.Chadwick)使用磁谱仪和改良了的盖革计数器测得的它的粒子能谱却是连续的[14,15]。

B.核的构成和质子的发现

在英国曼彻斯特大学，卢瑟福[16]与其助手盖革和学生马斯登 (E.Marsden)[17]的α-粒子对金属箔的散射实验证实了原子的核式结构模型，即原子由原子核和电子组成。原子的内部中心有一个极小致密带正电的“核”，即原子核。实验对决定原子性质的原子质量数A与原子核所带的电荷数的关系也有了一定的认识。实验测出了原子核的电量Ze中的核电荷数Z大约是原子质量数A的一半。在1911年，巴克拉(C.G.Barkla)从X–射线对轻元素的散射实验中也了解到原子中的电子数大约是这些元素原子质量数A的一半[18]。两个不同研究领域的实验结果都指出元素的原子质量数A是原子核内核电荷数的2倍或是核外电子数的2倍。在当时，人们已经知道原子质量数A的数值都接近于某一整数，在按元素的化学性质排列的元素周期表中已可以找到A的数值和各元素在周期表内的序号即原子序数。可是，这些原子序数与可测量物理量核电荷数Z间有什么关系呢？对此，1911到1914年，范登布鲁克 (A.Van den Broek)进行了分析研究[19−22]。在卢瑟福于1911年5月提出原子的核式模型后[16]，1911年7月范登布鲁克在《自然》杂志上撰文建议原子的α粒子散射实验中的核电荷数Z有可能与元素在化学周期表中的原子序数相等[19]。在1913和1914年，卢瑟福的助手莫塞莱(H.G.J.Moseley)卓有成效的工作使这些原子序数的数值通过相应元素的 X–射线标识谱得到了精密的测定[23,24]，从而确认或纠正了周期表中已有元素的次序，还预测了未知元素的存在和它们的原子序数即它们在周期表内的位置，解决了多年困扰化学界化学家们凭主观推测排序元素的难题，同时也确认了范登布鲁克的说法。1913年,玻尔(N.Bohr)把量子化概念引进有核原子结构理论描述氢原子核外电子的运动,圆满地解释了氢原子光谱线的波长变化规律[25−27]。根据当时的实验事实，玻尔从原子中的电子数目等于其原子序数角度也支持范登布鲁克的观点。1920年在卢瑟福实验室，查德威克用铜箔、银箔、铂箔替代金箔继续α-粒子的散射实验，直接测得了这些金属原子核的电荷，这些金属的核电荷数的测量值在1%的实验误差范围内与其原子序数值符合得很好[28]。从而又一次说明了范登布鲁克假定的正确性，为周期表中元素X(又通常记作)的原子序数Z赋予了相应的物理意义，还进一步证实了多种原子的中心都有个很小的核，即核式原子结构模型是正确的。那么很自然的重要问题就是：原子核又是由什么构成的呢？

实际上原子的核构成问题卢瑟福在1909年从尝试解释盖革与马斯登的α-粒子对金箔的大角散射实验数据时就提出来了[29]。1913年，范登布鲁克也建议原子核的电荷是电子与α-粒子相互抵消后的电荷[20]。从1909年到1914年，卢瑟福与纳托尔(J.M.Nuttall)的实验结果[30]以及达尔文(C.G.Darwin)和马斯登对α-粒子与氢原子和氦原子散射的研究结果都表明氢原子核有一个正电荷，而α-粒子或氦原子核有二个正电荷[29]。在1914年，卢瑟福又指出带正电的原子核内含有带负电的电子是合理的[29]。玻尔根据计算也得出结论β-射线来源于原子核[15,29]。于是卢瑟福根据当时的实验事实提出了所有原子的原子核是由 “正电子”和电子构成的，并自然地认为这样的“正电子”为氢原子核[29]。后者则是卢瑟福深受 100年前英国化学家普劳特(W.Prout)思想影响的推测。1815年普劳特根据他对当时已知化学元素的原子质量的测量结果曾假定氢原子之外所有元素的原子都是由不同数目的最基本的氢原子组成的[31]。根据这个“正电子”假说，卢瑟福进一步预测到：1个氦原子含有4个“正电子”和2个电子；1个电子与两个“正电子”相结合形成氢的同位素氘。也就是说，一个质量数为A和原子序数为Z的中性原子的核内会有A个“正电子”和A–Z个电子，其它的电子分布在核外的电子壳层上。1914年，达尔文计算出单次散射情况下受α-粒子碰撞后的氢气会产生出少量的氢原子[32,33]，因其质量较氦原子小，受正碰后其速度大约会为α-粒子的1.6倍。若考虑到斥力及氦原子的电量是氢原子的2倍，这个速度倍数应为4倍。马斯登在这一年进行的α-粒子通过氢气和空气的实验证实了上述推算结果[34]。当他把含有纯度大约100毫居里的α-射线的细管置放于充满氢气的管中时，他能从硫化锌屏幕上看到碰撞后产生的少量氢原子发出的快速运动的闪烁点，且其路径长度大约有20 cm。将氢气换为空气时，他观测到α-粒子的闪烁路径长度大约为5 cm。1917年，卢瑟福继续了1915年已回新西兰的马斯登的上述实验，也都在长射程处重复地观测到了与α-粒子碰撞后粒子的闪烁现象。之后，针对这种长程闪烁粒子的电荷正负性、数目多少、路径长度及粒子实质等诸方面，利用改进了的带有电磁铁的实验装置（如图1所示）和使用显微镜对快速运动发出闪烁点粒子的有效计数方法，卢瑟福在凯 (W.Kay)的协助下对α-射线通过氮气、二氧化碳和氧气时的吸收和碰撞行为特性进行了广泛和深入的研究。经过多次反复实验和仔细分析比较不同实验结果[35−37]，他们发现长射程闪烁粒子的产生不是来自空气中的二氧化碳、氧气、水蒸汽，而是来自空气中的氮气。同样实验条件下，从人造氮气中产生的长射程闪烁粒子数是空气中的1.25倍。1919年，卢瑟福总结得出结论[37]：长程闪烁粒子是带正电的氢原子核；高速α-粒子轰击氮原子将氢原子核从氮原子中打出来后，氮原子核变成了氧原子核，同时将氮原子变成了氧同位素原子。即经过了如下人工嬗变核反应过程

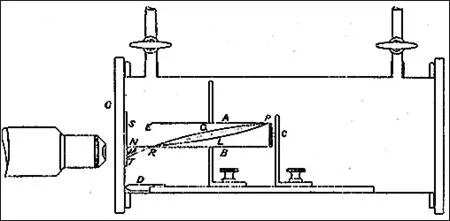
图1.1917年卢瑟福用 α-粒子对气体散射的实验装置示意图。水平狭缝AB长6.0 cm，宽1.5 cm，深8 mm；辐射源镭C的对面为硫化锌屏幕S；承载辐射源和水平狭缝的载体放在长方形黄铜盒内，由干燥空气或其它气体产生的电流会连续通过该铜盒；硫化锌屏幕S放在盖住铜盒的玻璃板上；铜盒则位于一个大电磁铁两极之间，其均匀磁场平行于极板平面和垂直于两极。α-粒子的直线经迹PM对应零磁场，从而可对准屏幕上的M处来调节显微计数器。当改变磁场为反方向时，α-粒子的上偏经迹PLRN反转为下偏经迹PQRT。加长杆D长1.2 cm，在辐射线的偏转量增加时使用[37]。

因此他认为氮原子核中含有氢原子核。1920年，卢瑟福将带正电的氢原子核建议称为质子 (proton)。到 1921年，卢瑟福与查德威克已经从硼 (B)、氟 (F)、钠 (Na)、磷 (P)、铝 (Al)等元素中打出了质子，证实了质子在多种元素原子的原子核中存在的普遍性[38]。

图2.α-粒子轰击氮原子过程的经迹照片[39]。

1925年布莱克特 (P.M.S.Blckett)等用计数自动控制的云室照相技术，自动拍摄到大量α-粒子轰击氮原子过程的经迹照片（如2所示）[39]，为氮原子核受α-粒子轰击释放出质子的核反应过程再次提供了确凿的实验数据。对照片中经迹的粗细与长短和弯曲形状与程度的分析结果更进一步清楚地证实了氮原子核中含有质子。

1927年春，丹尼森(D.M.Dennison)大胆地假定质子具有与电子一样大小为ħ/2的自旋[40]。正如本文作者曾指出的[41]，丹尼森的这个假设令人满意地解释了氢分子的转动比热实验曲线和仅用玻尔理论不能解释的氢分子光谱线强度的交替变化现象，使氢分子的两个令人多年困惑的实验结果的合理解释有了突破性进展，使人们对1924年提出的泡利不相容原理的内涵和理解清楚了许多。它促进了1927年泡利自旋理论的形式化，在量子力学的发展中有里程碑意义，推动了统计物理学中全同粒子统计与自旋关系理论的建立。

C.中子的发现

质子的发现为弄清原子核的构成提供了重要的实验事实。20世纪 20年代，物理学家们公认原子核是由质子和电子组成的。于是在1920年，卢瑟福曾推测一个电子与一个氢原子核在某些条件下会更紧密地结合成一个质量数为1的中性对子，它会呈现一些非常新颖的特性。例如，它的外部电场除了紧靠原子核以外的部分实际为零。因此它应能自由穿过物质，可能难于用光谱手段探测到它，也或许不可能密封储存它。另一方面，它应容易地进入一些原子的结构内，它或将被这些原子的原子核俘获，或将受原子核强场作用而被分解，从而可能产生出氢离子或电子或两者都有。卢瑟福称具有这些特性的粒子为中子(neutron)[37]。这些唯象推测为查德威克等卡文迪许实验室的研究人员从实验中寻找中子和后来分析相关研究结果从而发现和证实中子的存在起到了十分重要的指导作用。

1921至1931年，卢瑟福和查德威克与他们的学生在卡文迪许实验室做了许多实验来寻找卢瑟福预测的中子存在的证据。起初在1921和1922年，考虑到中子只有在强电场中形成的可能性，格拉逊(J.L.Glasson)[42],罗伯兹(J.K.Roberts)[43],以及查德威克用不同的电压激励氢气和一些稀有气体，曾尝试在气体放电时能找到中子的产生。后来为设法观测到中子，1928年前后查德威克等人改用天然放射性元素镭(Ra)和钋(Po)产生的射线来轰击铍(Be)等轻元素，又用盖革赠送他的盖革点计数器作探测器，还设计让不产生质子的辐射通过磁场，注重观测那些不发生偏转的辐射的闪烁点。其中盖革点计数器对α-粒子没有计数，因它们穿不透计数管的玻璃壁，所以计数管不会导电，这样它能压低信号的背底而提高探测器的观测灵敏度。注意到元素镭能产生α-射线、β-射线和γ-射线，而元素钋只放射α-射线以及α-射线轰击铍时不产生质子，查德威克与韦伯斯特(W.C.Webster)等人选用元素钋作为α-粒子的放射源轰击铍进行了多次有价值的实验。1930年6月，查德威克在费瑟(N.Feather)帮助下得到了放射性物质较强的镭D和它的产物钋源。在1931年6月的一次实验中，韦伯斯特发现沿着比反着入射α-射线方向的由铍发出的辐射线的穿透力强很多[44]。这些实验条件和初步结果为查德威克1932年初发现中子的后续实验积累了经验和打下了必要的工作基础。

1924年在德国联邦物理技术研究院(PTB)，盖革与助手玻特（W.W.G.Bothe,与玻恩共获1954年诺贝尔物理奖）改良了盖革–卢瑟福计数管。他们把两个计数管连接起来配上电子线路组成计数器，使射线粒子同时穿过它们且产生电离时才导电计数的办法有效地提高了计数器对射线粒子数目计数的效率。1930年，玻特和他的助手贝克尔(H.Becker)进行了用α-粒子轰击一系列轻元素和化合物的实验，用图3所示的静电探测器观测记录了它们产生的辐射[44]。被轰击的十四种元素其输出辐射的粒子数强度如图4所示[44,45]。由图可见，用α-粒子轰击铍时发出的射线强度比从轰击的锂(Li)或硼元素发出的射线强度都要大十多倍。这种射线能透过2 cm及其它厚度不同的铅板，铅板对该种射线的吸收系数只有0.3 cm−1。根据当时对已经发现的α-射线、β-射线和γ-射线穿透力的研究，玻特和贝克尔认为他们观测到了比不带电的γ-射线穿透力更强的新γ-射线，并将其称为 “人工激发的高能核γ-射线辐射”[45]。这些穿透力强的“高能核γ-射线”实际上是实验中首次发现的快中子流。因当时所用的计数器不能直接对中子响应等诸多原因，导致了他们没能把握进一步去确认新发现了中子的机会。

图3.1930年玻特和贝克尔用α-粒子轰击轻元素实验中使用的静电探测器[44]。

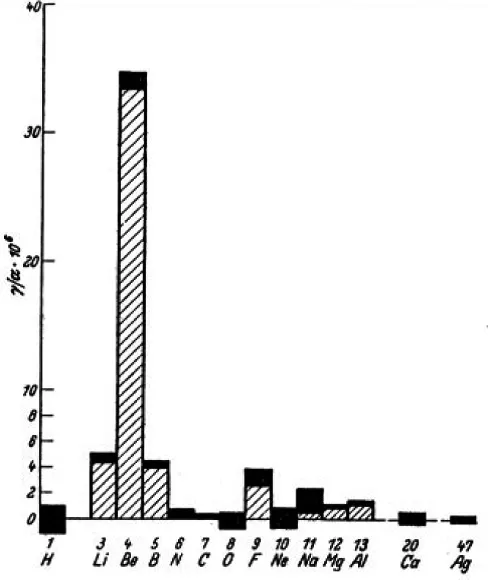
图4.α-粒子轰击的十四种元素输出辐射的粒子数强度。由图可见，铍是其中最有效的辐射元素[44,45]。

1924年在法国巴黎镭研究所的居里实验室，约里奥–居里夫妇（Joliot-Curie，皮埃尔–居里夫妇的女婿和女儿）也在进行镭的放射性研究，这时他们已从镭里提炼出大量的钋。1928年他们在《法国科学院通报》(Comptes Rendus de l’Acad´emie des Sciences) 上发表了精确测定由镭自发衰变产生的钋释放出的α-射线所产生的粒子数的文章[46,47]。1931年圣诞节期间，他们用带有载物薄窗口的常压空气电离室作探测器研究了由钋释放出的α-射线轰击铍和锂时所产生的新辐射对不同物质的作用特性。他们发现这种新辐射很容易穿透放在窗前的铝薄片或铅薄片，能够从石蜡、玻璃纸、水等含氢物质上打出高速质子流。他们测出这些质子的能量为5.3 MeV，并称这种新辐射为“γ-辐射”，即认为其辐射能量是从“γ-辐射” 中的光子同质子的康普顿效应过程中转化来的，但据此推算出α粒子轰击铍后所辐射出的这种“γ-辐射”的能量将高达50 MeV以上。1932年1月初他们在《法国科学院通报》上发表了这个重要的实验方案和结论[48]。约里奥-居里夫妇当时不知道卢瑟福对中子的预言，也没来得及进一步对实验结果做出令人信服的解释，但他们的这个实验方法和观测结果却极大地启发和激励了前期与韦伯斯特一起做过类似实验的查德威克。在韦伯斯特于1931年夏离开卡文迪许实验室后，这期间查德威克也正好一直在准备重新开始他们的那个实验。

图5.1932年1月查德威克发现中子实验装置的示意图[49]。

不同于约里奥–居里夫妇，查德威克则知道卢瑟福对中子存在及其特性的预言，对中子的概念早有考虑和实验上的探索经历。所以他会随即从约里奥-居里夫妇的实验联想到半年前他与韦伯斯特的实验。一番仔细地思考后，查德威克很快意识到约里奥–居里夫妇对其观测结果的解释有两个主要问题： (1)实验中观察到的质子散射的频率比用克莱因–仁科(Klein-Nishina)公式计算的结果要大数千倍；(2)根据能量和动量守恒定律很难解释从铍核与α-粒子相互作用后会产生一个50 MeV能量的“γ-辐射”光量子。于是，查德威克在1932年1月重开原来实验，对几种分子和原子重复了约里奥–居里夫妇的实验工作，实验装置示意图如图 5所示[49]。实验中他用了一个小电离室作探测器来探测被击出的质子与反冲核的脉冲幅度信号，然后经一个线性放大器放大后输入到记录示波器进行显示和记录。实验表明：α-射线轰击铍核后的辐射从元素氢、氦、锂、铍、碳、氮、空气、和氩气中都能打出粒子。从氢元素打出的粒子的速度像质子一样快到3.2×109cm/s，而且与激发α-射线相反方向出射的质子辐射范围比前向辐射范围窄得多。另外从其它元素打出的粒子有较大的电离能，每一种元素的原子都有反冲。这些实验结果都难于用认为α-射线轰击铍核后的辐射为光量子辐射的观点来解释。另一方面，若假设这些辐射是由质量为1、所带电荷为0的粒子即中子组成的，即α-射线轰击铍核产生了如下过程的核反应

则以上实验结果和现象都能按能量守恒定律和动量守恒定律得到很好得解释和理解。总结这些研究结果，在约里奥–居里夫妇的文章发表后不到一个月，查德威克在 1932年 2月 17日以 “Possible Existence of a Neutron”为题目投稿《自然》杂志宣布他发现了中子[50]。在 1932年 5月 10日的另一篇题目为 “The Existence of a Neutron”的文章里[49]，他报道了用α-射线轰击铍和硼产生的辐射对氢气、氦气、氮气、氧气、和氩气多种气体靶的作用数据，从中得出了一致的实验结论。

为确定中子的质量，由于当时铍原子的质量还没被精确测量，查德威克幸运地将铍改用硼，按以下(*)式所示核反应方程又较准确地确定了中子的质量，从而多方面进一步证实了原子核中中子的普适存在[49]。他假定中子是从硼的同位素发射出来的，即：

实验中，反冲氮核的速度即动能为0.00061u(u为质量单位)，测得的α-粒子和中子的动能分别为 0.00565u和 0.0035u。核反应方程 (*)式中硼原子、氦原子、氮原子的质量都已由阿斯顿 (F.W.Aston)用质谱的方法精确测定，它们依次分别为 11.00825(160)、4.00106(60)、14.0042(28)，括号内的数值为从小数点最后一位算起的测量误差。基于这些数据，根据粒子与靶的碰撞过程中动量守恒，查德威克求得了中子的质量为 1.0067(23)u，位于 1.004 u和 1.009 u之间。可见，中子的该质量值的确符合卢瑟福的预测，即它与质子质量很相近。另外，由于质子与电子质量的和为1.0078 u，这与中子质量间的质量亏损对应的质子与电子结合形成中子时所需要的结合能应为(1.0078−1.0067)u×931.5 MeV/u=1.025 MeV。于是，查德威克进一步认为，当结合能在1∼2 MeV情形下，可以假设中子的半径是10−15m的量级，在其中的质子和电子可以看作形成了一个小的偶极子，或设想是质子是嵌入在电子中。虽说这些估计和假想都是合理的，但需要精密地测定出中子的质量来更准确地确定出质子与电子的结合能。对此，这期间从宇宙射线中发现了正电子的事实和约里奥–居里夫妇利用α-射线轰击硼的同位素既能产生正电子也能产生中子的实验起了很大作用。1932年8月安德森(C.D.Anderson)宣布通过云室观测宇宙射线发现了狄拉克从理论上预言的正电子（质量和电荷与电子相等但带正电）[51]。安德森因此获得了1935年的诺贝尔物理学奖。其实约里奥–居里夫妇在1932年他们的放射性实验中也曾用云室清楚地观察到过正电子径迹，而且还是在安德森的发现结果公开之前。更有趣的是在2年后的1934年，约里奥–居里夫妇除了从类似如下的放射性实验结果中证实了安德森发现的正电子存在的真实性之外，他们还发现[52]：用α-粒子轰击的硼、铝、镁在发射出中子的同时，会分别生成一种自然界不存在的放射性同位素而这些放射性元素又分别在不同的时间后发射出正电子和生成另外一种稳定的原子。例如用α-粒子轰击硼会发生如下的核反应

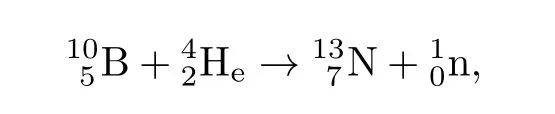
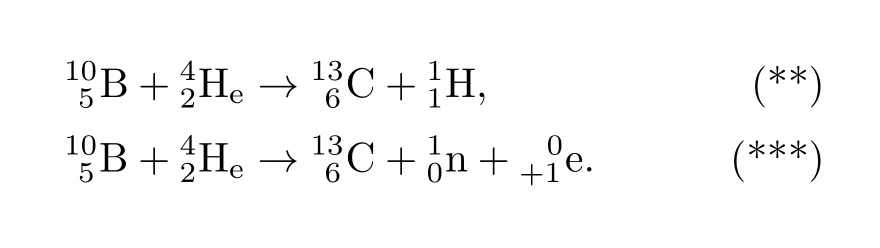
图6.1933年 10月在布鲁塞尔召开的第七次索尔维会议照片。坐者左起:E.Schr¨odinger,I.Joliot-Curie,N.Bohr,A.Ioあe,M.Curie,P.Langevin,O.W.Richardson,E.Rutherford,T.de Donder,M.de Broglie,L.de Broglie,L.Meitner,J.Chadwick。站者左起:´E.Henriot,F.Perrin,F.Joliot-Curie,W.Heisenberg,H.A.Kramers,E.Stahel,E.Fermi,E.Walton,P.Dirac,P.Debye,N.F.Mott,B.Cabrera,G.Gamow,W.Bothe,P.Blackett,M.S.Rosenblum,J.Errera,Ed.Bauer,W.Pauli,J.-´E.Verschaあelt,M.Cosyns,E.Herzen,J.D.Cockcroft,C.D.Ellis,R.Peierls,A.Piccard,E.O.Lawrence,L.Rosenfeld

联立该两式，由质子和正电子的质量以及反冲核与出射粒子反应前后的能量差，约里奥–居里夫妇求得了中子的质量为1.0098(5)u。可以看出，中子质量的测量精度在一定程度上依赖于某个核反应过程及其中反冲核与出射粒子的质量精度。由于中子不带电，显然测带电原子核质量的方法不适用于中子。考虑到氢的同位素氘的质量亏损小，可用大于其结合能的高能γ-射线将其分裂，所以在1934年8月，查德威克和他的博士生戈德哈伯(M.Goldhaber)进行了用γ-射线轰击氘核的实验[54]。实验证实发生了如下光致核反应过程

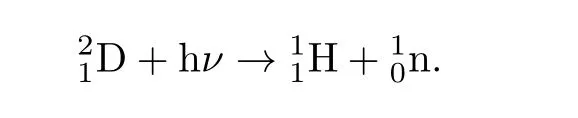
由于当时氘质量的测定值 2.01363(4)u和质子质量 1.007775 u都已精确知道，所以从实验中使用的氘的结合能2.1 MeV，查德威克他们精密地确定出中子的质量为1.0080(5)u。至此，查德威克的一系列决定性的工作令人信服地证实了中子的存在。1935年，在约里奥–居里夫妇获诺贝尔化学奖的同年，他因中子的发现获得诺贝尔物理学奖。

D.原子核是由质子和中子组成的

图7.伊万年科1932年4月在《自然》上的全文内容[51]。

中子的发现证实了卢瑟福原子核中存在中子预言的同时，也向原子核是由质子和电子组成的假说提出了挑战，因为这时似乎应该说原子核是由质子和电子及中子组成的。由于中子被视为质子和电子结合成的中性对子，所以中子发现后的大约2年时间里，包括查德威克在内的许多人仍坚持认为原子核是由质子和电子组成的。虽然从原子核中放出的α-射线和γ-射线不连续的能量可以用原子核里分离的不同能级间跃迁时的释放能来解释，然而，支持核里有电子观点的重要实验事实β-射线的能量却是连续分布的，这似乎与处于微观的原子核的能量是量子化的事实不一致，好像这时候已发展起来并取得巨大成功的量子力学方法不适用于原子核内部，甚至玻尔认为β-衰变过程中能量守恒和动量守恒定律都不成立[15]；另外在与原子核自旋、核自旋统计及核自旋磁矩等问题上也得出与实验结果不符的结论。例如，从氮气的分子光谱得到氮原子核(147N)的自旋角动量量子数I的实验值为1和服从玻色–爱因斯坦统计[55]。但是按照原子核由质子和电子组成的假设，核内该有14个质子和7个电子。由于质子和电子的自旋角动量都是ħ/2，它们间的任何平行和反平行合成都使其总自旋角动量量子数为半整数，而不会为整数。为解决当时一系列困惑，几位科学家们分别相继独立地提出了中微子假说和原子核是由质子和中子组成的假说。1930年 12月，泡利(W.E.Pauli)提出了现在称为中微子(neutrino)的假说[15]。他指出原子核中还存在一种质量很小甚至为零的电中性粒子，它的自旋为 ħ/2，它有磁矩，它在β-衰变过程中与电子同时被发射出来，使它们的能量之和为常数。直到1933年10月在布鲁塞尔召开的第七次索尔维会议(会议照片参见图6[15])上，泡利才首次公开发表了以上中微子假说。这之前，实际上很多科学家都很知晓他的这一思想。而且，核内的粒子好像成了质子、电子、中子、和中微子。另一方面，就在查德威克1932年2月发表发现了中子后的半年内，伊万年科(T.D.Ivanenko)相继在杂志上发表了原子核是由质子和中子组成的观点。在《自然》上的全文如图7所示[51]。该文中伊万年科指出了核内不含电子的可能性，强调了视中子为像质子和电子那样当作“基本粒子”的巨大兴趣，假定了中子的自旋是ħ/2。另外他对铍核不含自由质子却只含α-粒子和中子的观点也好奇。1932年9月，巴彻(R.F.Bacher)和康登(E.U.Condon)也意识到：若认为氮原子核含有7个质子和7个中子且中子有与质子或电子相同的自旋ħ/2，则上述氮原子核的自旋为1的困惑可以解决[57]。在1932年的6月、7月、12月海森堡 (W.Heisenberg，这一年海森堡获得诺贝尔物理学奖)连发了三篇论文[58−60]。他将中子作为原子核的组成成分之一，通过讨论质子和中子间的相互作用以及对使原子核结合在一起的核力的动力学描述和研究，也指出原子核是由质子和中子构成的。海森堡统称质子与中子为核子(A nucleon is either a proton or a neutron.)，并把质子与中子看作核子的两个不同量子状态。那么，质子和中子之间能否相互转变呢？在它们的转变过程中又会产生什么呢？1934年1月，费米(E.Fermi)提出了β-衰变的定量理论[61]。由于质子和中子分别属于核子的不同量子态，它们之间的相互转变相当于核子从一个量子态到另一个量子态的跃迁，在跃迁过程中同时放出电子和中微子。原先核内并没有电子和中微子，它们是核子量子跃迁的产物。正好像光子是原子不同量子状态之间的产物一样，光子原先并不存在于原子内。导致产生光子的是电磁相互作用，而这里导致产生电子和中微子的是自然界中除了已知的引力和电磁力以外的第三种相互作用：弱相互作用。β-衰变就是核内一个中子通过弱相互作用衰变成一个质子、一个电子和一个反中微子¯νe（即自旋与动量同向的中微子；右下角标e表示伴随电子或正电子而产生）。这个过程可用下式表示

β-衰变过程中由于电子与中微子同时被发射出来且它们的能量之和为常数，所以这个常数能量可在电子与中微子之间任意分配，从而产生连续的β-射线能谱。费米β-衰变的理论对此做出了定量地描述。他还预言了质子衰变成中子的过程中会产生一个正电子和一个中微子（中微子的自旋方向与动量方向相反）。这个过程可用下式表示

可见，中微子假说和原子核是由质子和中子组成的假说解决了上述及其之外相关的一系列困惑，明确了量子力学和能量与动量守恒普适于原子核内部的问题。那么能否从实验中发现中微子的存在呢？由于中微子不带电，质量又近乎为零，所以在实验中极难测量。1942年王淦昌提出了用K俘（原子核俘获核外K壳层上的一个电子而转变为另一种原子核的过程）来间接探测中微子的方法[62]，并由戴维斯(R.Davis)在1952年得到了实现[63]。因为K俘获没有β-粒子放出，只有中微子产生，例如的K俘获核反应过程为

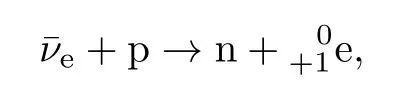
柯文(C.Cowan)和莱因斯(F.Reines)等在1956年第一次通过实验直接探测到了反中微子[64]。这个发现使他们于1995年获得诺贝尔物理学奖。

E.核自旋与核自旋磁矩

原子核是由质子和中子构成的，而质子和中子各自都有轨道角动量和自旋角动量，所以原子核内所有质子和中子的轨道角动量与自旋角动量矢量之和就是原子核的角动量，通常称为原子核的自旋，简称核自旋。有时有人也习惯简短地说“这个原子核的自旋是I”，这句话指的是这个原子核自旋角动量的最大可测量分量是Iħ。

质子和中子的自旋都是ħ/2。实验测得的 29种原子核基态时的自旋I（以ħ为单位）及其核自旋磁矩µNz（以核磁子µN为单位）如表 I所示。可以看出：当质量数A为奇数时，I是ħ的半整数倍；当质量数A为偶数时，I是ħ的整数倍或零。自旋为ħ/2的奇数倍的粒子统称为费米(Fermi)子。因为质子和中子都是费米子，故奇数个核子组成的原子核自旋是ħ的半整数倍 (1/2，3/2...)。自旋为 0或为 ħ的整数倍的粒子统称为玻色(Bose)子。

III.核自旋变体与氢分子和乙烯分子的核自旋变体

A.核自旋变体与氢分子的两种核自旋变体

由两个或两个以上原子组成的分子的行为通常表现为分子的振动(vibration)和转动(rotation)等几种形式的运动以及电子运动与原子核自旋行为。由于分子中原子核的质量比电子质量大很多，从而核的动能比电子要小得多。因此在玻恩–奥本海默(Born-Oppenheimer)近似中，一个系统的总哈密顿量可近似为这些哈密顿量的和，而用来描写这个分子系统量子状态的总波函数则可近似写为描述这些对应行为的波函数的乘积，即：

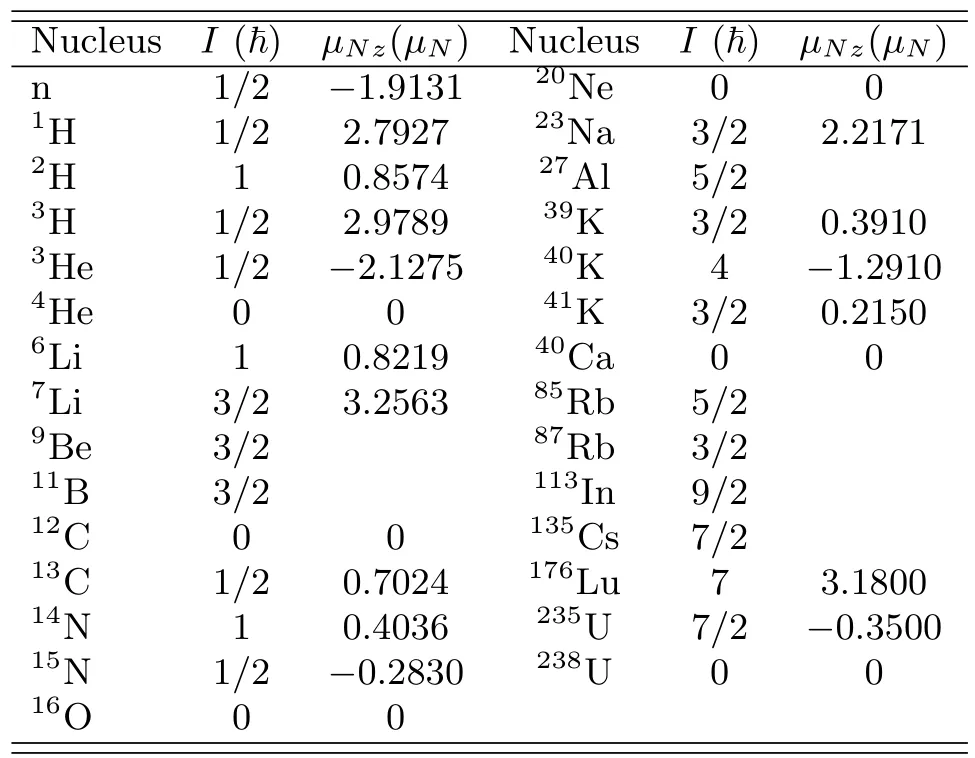
表I.实验测得的一些原子核的自旋I及其核自旋磁矩µNz

当分子中两个相同原子相互交换（即位置进行空间反演的同时自旋互相交换）时，分子总波函数的对称性可能发生变化，由其四个波函数各自的对称性决定。由于波函数Ψvib在分子的振动基态和波函数Ψe在电子基态1Σ态都不改变它们的交换对称性，因此转动波函数Ψrot与核自旋波函数Ψns的对称性决定分子总波函数的对称性。泡利不相容原理要求由多个全同费米子组成的分子的波函数服从费米–狄拉克统计，分子的总波函数为反对称波函数。由多个玻色子组成的分子体系服从玻色–爱因斯坦统计，例如氘分子(D2)和氮分子(14N2)，分子的总波函数为对称波函数。以下以中心对称线型非极性同核氢分子为例说明分子的核自旋变体的形成及其辨识。

氢分子的每个氢原子由一个质子和一个电子组成。由于氢原子核即质子是费米子，氢分子的波函数为反对称波函数，所以波函数乘积ΨrotΨns应为反对称波函数。在球坐标系中，氢分子的转动波函数是球谐函数，在空间反演变换 (θ,φ)→(π −θ,π+φ)绕通过分子质心的垂直轴旋转180°后的波函数为原波函数的(−1)J倍，这里J为转动角动量量子数。也就是说J值的奇偶性能决定转动波函数的空间反演对称性（即宇称）分别是反对称波函数和对称波函数。取空间向上为量子化方向轴，可以用分别与此轴平行和反平行的描写单个原子核自旋角动量的波函数α和β的组合构成氢分子的原子核自旋波函数Ψns。对应平行于和反平行于量子化方向轴的两个氢原子核的自旋方向，我们可有如下形式的表示：

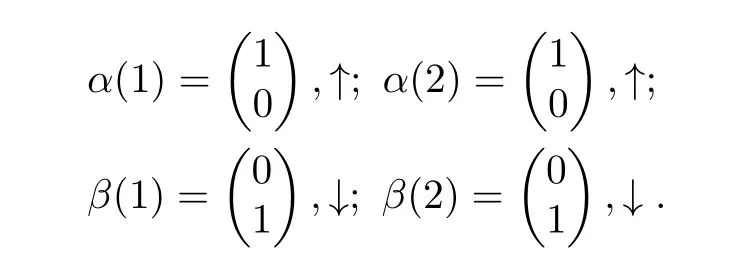
于是，氢分子的核自旋波函数Ψns应是下列函数之一：

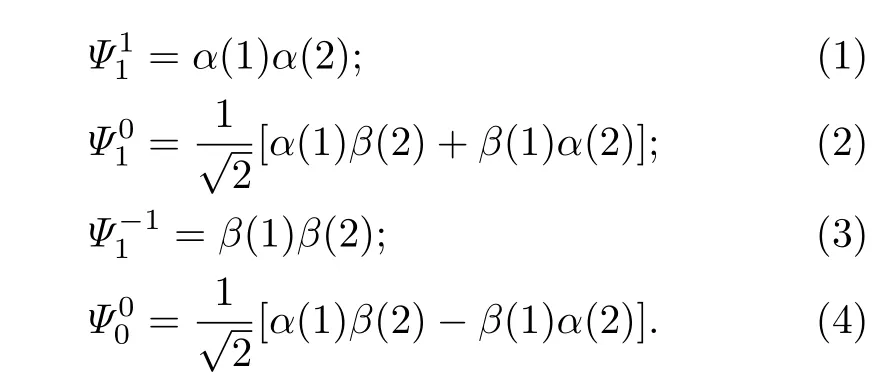
交换数字1和2，即交换两个原子核的自旋变量，可以看出前三个波函数不变号，所以它们是对称的自旋波函数；公式(4)中的波函数改变符号，它是反对称自旋波函数。前三个对称自旋波函数描述两个原子核的总自旋角动量量子数为I=1的三重态，分别对应总自旋磁量子数MI=1，0，−1。这时，由这些波函数描写的氢分子的两个氢原子核的自旋方向平行，这类氢分子称为正氢，如图8a所示。最后一个反对称自旋波函数描述两个原子核的总自旋角动量量子数I=0及其总自旋磁量子数MI=0的单态。这时两个氢原子核的自旋方向反平行，如图8b所示，这类氢分子称为仲氢。正氢和仲氢称为氢分子的两种核自旋变体。这里，我们将核自旋变体定义为由于分子中对称位置上的同种原子的核自旋状态的不同而引变出的新分子。综合上述讨论中关于波函数Ψrot和Ψns的对称性，我们知道三重态的核自旋波函数与J为奇数的转动波函数的乘积使得ΨrotΨns为反对称波函数，从而氢分子的总波函数为反对称波函数。所以我们可用量子数J的奇偶来辨识正氢和仲氢。如图9所示[41]，正氢分布于奇数转动量子数J=1,3,5...的能级上，仲氢分布于含零的偶数转动量子数J=0,2,4,...的能级上。可以看出，最低两个能级中正氢的能级高于仲氢 121.706 cm−1，该能级差相当于温度174.98 K，它远高于正常氢的沸点 20.369 K和仲氢的沸点 20.277 K[41]。所以，当将氢气冷却到20.4 K并达到平衡时，几乎所有的分子都处于J=0的的最低转动能级态上，仲氢和正氢分子浓度各占约99.82%和0.18%。1929年,潘霍华(K.F.Bonhoeあer)和哈特克(P.Harteck)根据该原理用冷却方法成功地制备出纯仲氢[65]，有力地证实了氢分子的两种核自旋变体的存在。

图8.（网络版彩色）氢分子的核自旋变体：a)正氢(ortho-H2)，b)仲氢 (para-H2)

图9.（网络版彩色）氢分子的能级B0J(J+1)按转动角动量量子数J的分布图[41],B0是转动常数。

B.乙烯分子的四种核自旋变体

如图 10所示，乙烯 (C2H4)分子由四个氢原子和两个碳原子组成，两个碳原子之间以共价键双键连接。原子之间键长及键角等分子结构参数为：rCH=1.0869 ˚A，rCC=1.3391 ˚A，αCCH=121.28°，αHCH=117.4°。乙烯分子的结构是一个平面结构，属于高对称性的D2h点群。图 10所示的原点在分子质心并和分子一起运动的直角坐标系与经典著作中的取法相同[66−69]。其中x,y,z轴分别与分子的惯量主轴a,b,c重合；含x轴平行于C=C双键的x-y平面为分子平面；通过分子质心的y轴在x-y平面内垂直于x轴，z轴垂直于x-y平面和x与y轴并指向纸面外。在该坐标系下，乙烯分子D2h点群下的8种不可约表示在恒等操作 E、旋转操作 C2、 按对称中心反演操作i、和镜面操作σ下的特征标表如表II所示[69,70]。表II中间各行的数字1表示操作不改变符号，即对这些操作是对称状态；数字−1表示操作改变符号，对这些操作是反对称状态。如果进一步有对称中心，g表示对称，u表示反对称。最末一栏的R表示绕相应分子轴旋转零度或180°。由此可知，乙烯分子的转动波函数在D2h点群下可用Ag，B1g，B2g，B3g四个不可约表示来分类组合，而且Ag和B3g是偶宇称，B1g和B2g是奇宇称。

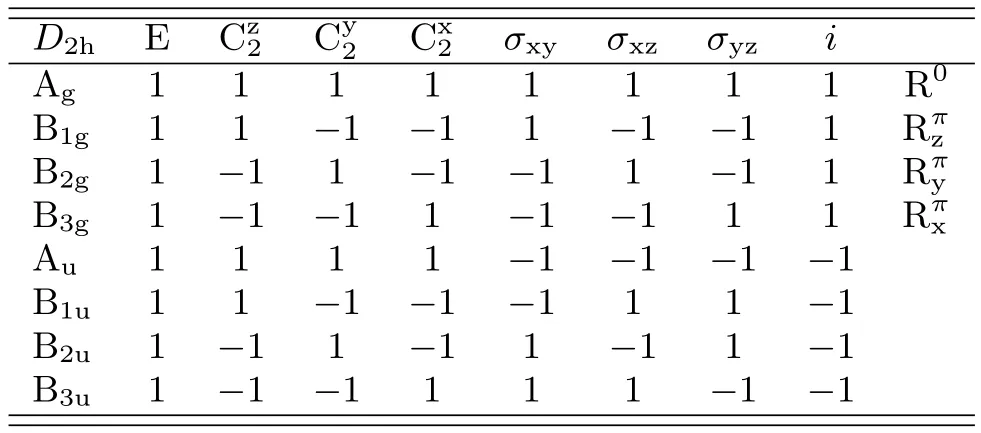
表II.乙烯分子D2h点群下的特征标表

表III.乙烯分子的四种核自旋变体及其对应的转动能级态JKa,Kc的量子数Ka和Kc的奇偶[69]

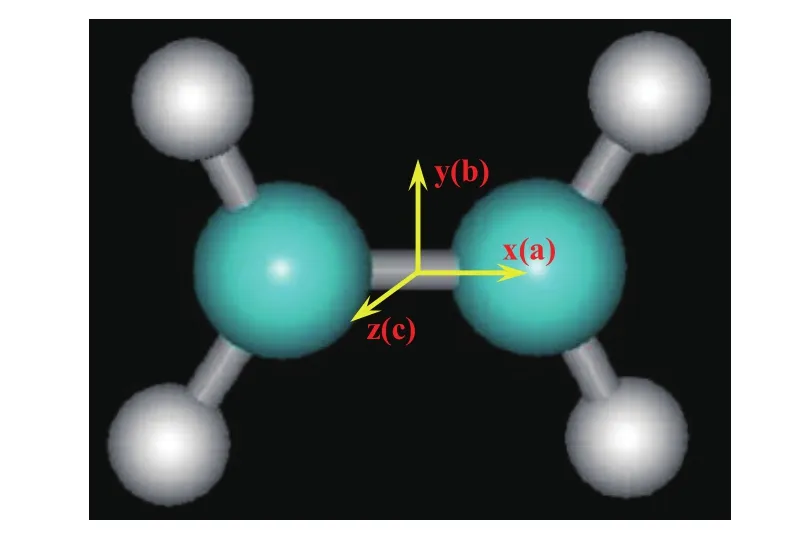
图10.（网络版彩色）乙烯分子结构和分子固定直角坐标系。

乙烯分子的两个碳原子的核自旋为零，四个氢原子核的自旋为ħ/2。对应四个氢原子核的自旋方向向上和向下，乙烯分子有16(24)个独立的核自旋波函数。不同于两个质子自旋方向的平行和反平行形成正氢和仲氢那样直观，乙烯分子的这16个核自旋波函数与四个转动波函数的不可约表示按泡利不相容原理在D2h点群下构成 Ag，B1g，B2u，B3u四种不同核自旋变体[69]，它们分别对应D2h(M)分子对称群下的 Ag，B1g，B2u，B1u四种核自旋变体[70,71]，对应总核自旋角动量量子数I=2，1，0。在Ag状态统计权重为7，其中四个氢原子核的自旋方向都平行向上，对应I=2，统计权重为5；或对应I=0，四个氢原子核的自旋方向两两平行向上和向下，各自的统计权重都为1。表II中所有绕分子轴x，y，z轴的旋转操作都对应2个氢原子的相互置换，它们在Ag状态都为对称状态。由于乙烯分子不同转动能级态由JKa,Kc确定，根据泡利不相容原理需要跃迁谱线的低能态中量子数Ka和Kc都是偶数。这里Ka，Kc分别表示转动角动量量子数J沿图10中坐标系a轴和c轴的投影分量。B1g，B2u，B3u三种核自旋变体都对应I=1和统计权重都为3。在B1g状态的核自旋波函数绕z轴旋转180°是对称的，但对绕x轴或y轴旋转180°是反对称的。所以泡利不相容原理要求量子数Ka是奇数而Kc是偶数。同理，在B2u状态的核自旋波函数绕y轴旋转180°是对称的，绕x轴和z轴旋转180°是反对称的，这时要求量子数Ka和Kc都是奇数；在B3u状态的核自旋波函数绕x轴旋转180°是对称的，绕y轴和z轴旋转180°是反对称的，所以泡利不相容原理要求量子数Ka是偶数而Kc是奇数。平面非对称陀螺分子乙烯的转动能级的宇称由式子(−1)Kc确定，可用g和u分别表示其转动能级的偶宇称和奇宇称[69]。表III给出了以上描述的这四种核自旋变体的统计权重及其相对应的振转基态下的不同转动能级态JKa,Kc的量子数Ka和Kc的奇偶。由上所述，我们根据跃迁谱线的低能态中量子数Ka和Kc的不同组合便可辨识乙烯分子的四种核自旋变体。例如，90,9←101,9这条P-支谱线低能态的Ka和Kc分别是奇数1和9，所以泵浦这条谱线便可获得B2u核自旋变体的信息。同样，对应Ka和Kc的其它3种组合我们分别得到乙烯分子的B1g，B2u，B3u另外3种核自旋变体。

IV.乙烯分子的核自旋变体的分离及其相互转换

A.乙烯分子的核自旋变体的分离及其相互转换研究的实验方案和实验装置

核自旋变体的研究不仅能揭示一些基本的量子力学规律，其实验结果还具有潜在的重要应用。虽然早在1912年就已经初步开始研究正氢和仲氢了，但对其它多原子分子在这方面的研究却很有限。到目前为止，仅研究了6种多原子分子的核自旋变体的分离和转换，并且这些分子都只有正(ortho)和仲(para)两种核自旋变体。与此不同，我们通过设计实验，研究了乙烯分子的四种核自旋变体的分离和转换量子特性。乙烯分子有着许多重要的应用:(1)乙烯是世界工业中产量最大的化学中间转换体之一，是合成塑料、合成橡胶、合成纤维、合成酒精的基本化工原料；乙烯工业是石油化工产业的核心；(2)乙烯是存在于木星、土星、海王星等大气中重要的碳氢化合物；(3)乙烯是植物中具有异常信号传递路径类似荷尔蒙的最简单的分子之一；乙烯具有一定的生理效应等等。

乙烯分子的ν7振动带的中心大约在 1000 cm−1，它的P/Q/R-支谱线的吸收频率与许多CO2激光输出谱线频率有良好的匹配。例如乙烯分子的90,9←101,9这条P-支吸收谱线，其跃迁频率比10P(44)CO2激光谱线的频率仅高出30 MHz，位于多普勒吸收谱线的线宽内。所以，我们可以使用CO2激光来激发一些含有核自旋变体信息的乙烯分子谱线。乙烯分子10µm波带的高分辨率红外光谱中的分子跃迁频率和许多谱线的能级值已精密测定，我们还可以根据乙烯分子高分辨率光谱中分子的谱线标识，正确归类各自的核自旋变体和计算它们的跃迁频率与CO2激光输出谱线的频率差。实验中选择的乙烯分子的跃迁谱线和CO2激光输出谱线以及对B2u核自旋变体的分离与核自旋变体间转换的实验方案如表IV所示[69]。下面着重介绍我们是如何将其中的一种核自旋变体与其它的三种分离开来；在它们的转换分布即分子重新恢复到其自然的热平衡态过程中，我们又观测到了哪些现象；我们对这些实验现象和实验结果的理解分析及其所对应的物理机制的探讨。

我们开发的实验装置的框图如图11所示[69]。实验中我们使用了两台 CO2激光器。一台是有大功率输出的PL3系列激光器，用于核自旋变体的分离。另一台是根据美国标准计量局Evenson的设计我们自制的CO2激光器。使用腔外兰姆凹陷的稳频技术，我们可以保持它的输出功率在长时间里稳定，因而实验中它被用作探测激光器，探测由于核自旋变体的分离和相互转换而引起的光谱谱线强度的微弱变化。分离用气体室是直径2 mm和长1 m的耐热玻璃毛细管，管的两端用布儒斯特窗密封。实验中，我们调谐PL3激光器的10P(44)CO2激光输出频率比乙烯分子的90,9←101,9这条P-支吸收谱线的跃迁频率大约低 30 MHz，将输出功率约为6 W的10P(44)CO2激光束聚焦进入分离用气体室里激发B2u核自旋变体，从而将其与其它三种核自旋变体分离出来。将第二台自制的CO2激光器调谐到探测用的激光线，直接探测或借助声光调制器AOM移频探测它们对应的乙烯分子吸收光谱线强度的变化，从而获得所对应的四种核自旋变体的信息。从探测激光器输出的激光束经分束器和斩光器斩为位相相反的两束光后，将它们同时聚焦进入两个设计上相同的试验气体样品室和参考气体样品室。这两个玻璃样品室的直径是3 mm、长为20 cm。最后，从试验气体样品室和参考气体样品室输出的两条激光束的强度差用HgCdTe探测器探测后输入到锁相放大器处理，再输入到计算机中进行实验信号的显示和数据储存或处理分析。

我们按以下步骤观测和记录实验信号。由于1米长的分离气体室与试验气体样品室是用玻璃阀门T连在一起的，所以当阀门T打开时，气体分子可以在分离气体室和试验气体样品室之间移动。参考气体样品室与一个大容积的乙烯气体室相通。前面提道HgCdTe探测器记录的是从参考气体样品室与试验气体样品室输出的两条激光束的强度差。很显然，当分离用的CO2激光没有穿过分离气体室时，HgCdTe探测器记录到的这两条输出激光束的强度差应该为零。这样，我们记录这条强度差为零的基准线1分钟。紧接着在第60秒，让10P(44)CO2激光射入分离气体室历时3分钟，从而使B2u核自旋变体在这3分钟里被浓缩而与其它核自旋变体分离开。3分钟后也就是在第240秒时，关闭阀门T从而将分离气体室与试验气体样品室隔离开。之后，处于非平衡态的核自旋变体要向其自然分布状态重新分布转换以恢复到它们原有的热平衡态。于是，我们就在40多分钟的时间里观测和记录变化的转换信号。

B.光诱导 B2u核自旋变体分离的实验观测结果和分析

按以上步骤记录到的典型实验信号曲线如图 12和 13所示，分别对应于 B2u，B3u和 Ag核自旋变体[69]。图中的纵轴是光谱线强度的变化值，横轴是时间。如图所示每条实验曲线都由3部分组成。第1部分是谱线强度差为零的零基准线。曲线的第2部分对应核自旋体分离的结果。我们可以看到B2u核自旋变体作为吸收分子其浓度被 10P(44)CO2激光浓缩降低了，而B3u和Ag作为缓冲分子成份其浓度增强了。在分离激光器的输出功率为 6 W、以约 30%的透过率穿过压力为 1 Torr的分离气体室 3分钟的条件下，测得B2u核自旋变体的浓缩度大约为3%，B3u和 Ag核自旋变体的增强度差不多各是 1%。这些数据表明 B2u核自旋变体在激发态的碰撞横截面较其基态的碰撞横截面大约增大1%。以上测量结果以及相应跃迁谱线的吸收系数分别表示于表IV的第6和第7栏中。为什么我们能把B2u这种核自旋变体与其它的3种分离开呢？又为什么B2u核自旋变体的浓度减少了而其它3种核自旋变体的浓度增强了呢？这可以从光诱导漂移的原理中加以理解[41,68,69,72]。在分子物理学中，当激光的频率调谐到与分子的跃迁频率相同时，分子将对激光的输出功率有最强的吸收，在以此为中心频率其左右60 MHz的光谱多普勒吸收包络内的分子都能不同程度的吸收该激光。包络以外的分子可称为缓冲气体分子。现在让一束激光通过一个充有低压气体的密封气体室时，如果将该激光的频率调谐到多普勒吸收轮廓的低频区域，这时以一定速度朝着激光方向移动的一群吸收激光的气体分子由于多普勒效应将被激发。与基态的分子相比，由于这些被激发了的分子通常有较大的横截面，因而就有较短的平均自由程。相对于缓冲气体分子而言，根据动量守恒定律，这就产生了沿着激光方向移动的吸收激光的分

子的漂移，从而会导致密封的气体室两端的气体浓度有差别。这就引起了与分离气体室的激光入射端相连的试验气体样品室中B2u核自旋变体浓度的减少和其它3种核自旋变体浓度的增强。对应分离时间为3分钟，乙烯的气压为1.44 Torr，实验中测得的B2u核自旋变体的衰减浓缩度为 (2.46±0.20)%(图 12)；气压为0.98 Torr，B3u核自旋变体的增强浓缩度为(0.91±0.05)%(图 13A)；气压为 1.02 Torr，Ag核自旋变体的增强浓缩度为 (0.89±0.05)%(图 13B)。气压由数字式MKS Baratron真空计测量。方案中探测情形6的 2610,16←279,18跃迁谱线强度太弱，实验中没观测到其对应的B1g核自旋变体分离前后谱线强度的变化。

表IV.乙烯分子的B2u核自旋变体的分离和核自旋变体间的转换实验方案和观测结果[69]。吸收系数β的单位为cm−1Torr−1

图11.（网络版彩色）实验装置的框图 [69]。L1,L2,空间滤波器;M1-M9,平面镜;BS1和 BS2分别是反射/透射比为 1:9和1:1的分束器;L3,焦距为25 cm ZnSe透镜;AOM,声光调制器;RF driver,射频声光调制器驱动器;T,R,S,玻璃阀门。

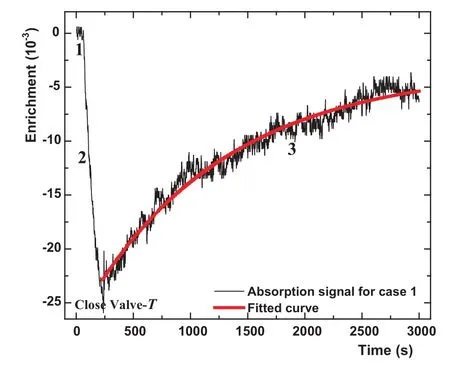
图12.（网络版彩色）在表IV实验方案情形1用10P(44)CO2激光谱线探测记录到的乙烯分子气压为 1.44 Torr时B2u核自旋变体的吸收信号。锁相放大器时间常数为0.3 s[69]。

C.乙烯分子四种核自旋变体转换中的宇称守恒及其核自旋变体间的转换观测结果与分析

图12与图13A和图13B中吸收信号的第3部分反映了阀门T关闭后由非平衡状态向自然平衡状态分子重新分布，从而核自旋变体间相互转换时其浓度变化的过程。可以看出，Ag核自旋变体的浓度几乎不随时间变化；然而，B3u和B2u核自旋变体的浓度却分别减弱和增强了。我们可从下述的宇称守恒假设和能态混合理论[73]来分析理解观测到的这些转换实验现象及其对应的物理机制[69]。

图13. （网络版彩色）(A)在表 IV实验方案情形 4用10R(22)CO2激光谱线探测记录到的乙烯分子气压为0.98 Torr时B3u核自旋变体的吸收信号;(B)在表IV实验方案情形5用10R(28)CO2激光谱线探测记录到的乙烯分子气压为1.02 Torr时Ag核自旋变体的吸收信号。锁相放大器时间常数都为0.3 s[69]。

在我们的实验中，乙烯分子的四种核自旋变体间的相互转换有6种可能性。现在我们假设同宇称的核自旋变体间的相互转换是允许的，而不同宇称的核自旋变体间的相互转换是禁戒的。显然，正如图13B所观测到的那样，Ag或B1g核自旋变体的浓度将不随时间而变，但B2u和B3u核自旋变体间的分子要在通过碰撞的重新分布中发生相互转换。如果同宇称的核自旋变体中有如下这样结构的分子能级，例如图14所示的能级在900 cm−1附近的B2u和B3u核自旋变体的能级对µ和µ′，它们的能级非常接近。能级相近的µ和µ′能态可能会由于一种量子微扰势能ħV而混合起来，这种微扰可能是来自核自旋与转动或者核自旋与核自旋间的弱相互作用。在这样的能级分布中，B3u能态的分子，当它们由于热运动来到这个能级µ′附近时，就会有机会通过微扰ħV进入到B2u能态µ，也会由于分子间的进一步碰撞而滞留在B2u能态。这样，随着时间的变化，B2u核自旋变体的分子吸收谱线强度会逐渐增强而B3u核自旋变体的吸收信号强度由于分子数的减少而渐渐减弱，两者向着低于零基线的它们新的共同平衡状态相互转化。

根据上述能态混合理论，恰波夫斯基 (P.L.Chapovsky)提出了两种核自旋变体间相互转换的“量子弛豫”模型[74]。从分子的态密度矩阵方程出发，他得到在任意时刻t核自旋变体 ortho(正)或para(仲)的非平衡浓度的弛豫释放率可用如下指数函数描述，

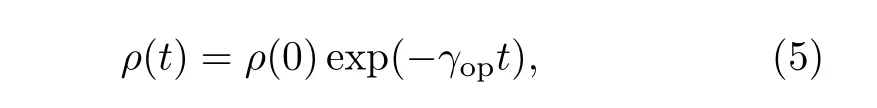
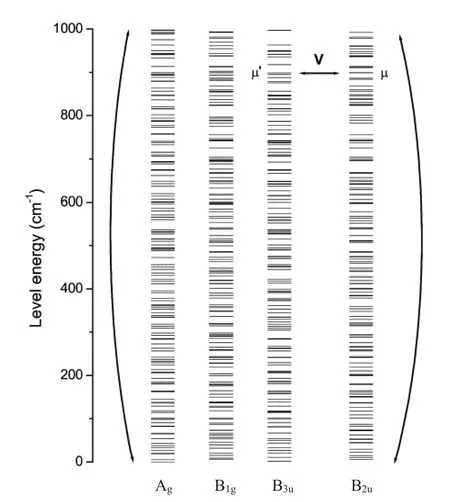
图14.(网络版彩色)乙烯分子四种核自旋变体的转动能级图[70]。

其中γop是正和仲两种核自旋变体间的转化率，可用下式表示

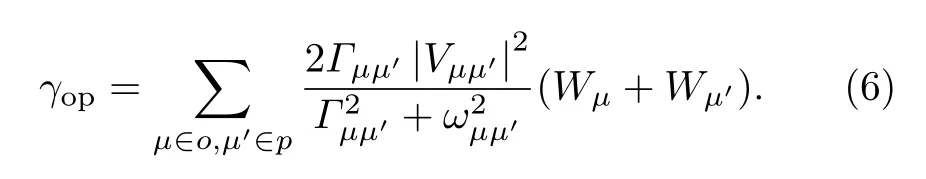
(6)式中，Wµ和Wµ′分别是µ和µ′能级态的玻尔兹曼因子，它们决定核自旋变体在不同时刻t在对应能级上的分布；ωµµ′/2π是相近能级对的间隔；Vµµ′代表能级µ和µ′间相互作用微扰矩阵元；Γµµ′是与气体压力成正比的压力展宽系数。在低压和压力展宽系数平方远小于相近能级对间隔平方的条件下，从 (6)式中容易得到γop正比于Γµµ′，从而也正比于样品室气压p。于是，对乙烯分子的B2u和B3u核自旋变体，根据该量子弛豫理论，我们用最小二乘法将图12和图13A中核自旋变体转换信号的实验曲线拟合于方程ρ(t)=ρ0exp(−γt)+ρ′(这里ρ0和ρ′分别代表累计信号强度和相对于公共零基线的信号偏移)，分别得到了它们所对应的转换率 (8.09±0.10)×10−4s−1(图 12) 和 (7.55±0.04)×10−4s−1(图 13A)。用同样的方法，我们得到在其它许多压力下观测记录到的转换实验信号的不同转换率，对同一气压下的核自旋变体的转换率求平均值后，得到了如图15A和图15B所示的转换率对气体压力的实验数据点[69]。可以看出，无论对于B2u或B3u核自旋变体，观测得到的转换率γ与压力p的关系曲线都是线性函数。于是，我们用最小二乘法将图15A和图15B中转换率的实验数据点分别拟合于关系式γ=k×p+d，得到γB2u=[(5.79±0.59)×p+(1.59±1.17)]×10−4s−1(图 15A)和γB3u=[(5.05±0.57)×p+(2.57±0.83)]×10−4s−1(图15B)。可以看出，B2u和B3u核自旋变体间的转换率在实验误差范围内相互自洽，符合得很好。这表明乙烯分子的四种核自旋变体在量子弛豫过程中遵循宇称守恒发生相互转换。

图15.(网络版彩色)B2u和 B3u核自旋变体间转换率的压力关系实验曲线 (A)对应 10P(10)激光谱线探测 B2u核自旋变体；(B)对应10P(26)激光谱线探测B3u核自旋变体[69]。

为从理论上阐明乙烯分子的这些新奇量子实验现象，定量描述引起乙烯分子核自旋变体转换的微弱相互作用势能 ħV，恰波夫斯基发表了他们近年的新成果[70]。根据实验确定的分子结构参数，他们计算出了如图14所示乙烯分子的四种核自旋变体的转动能级及其能级间隔。通过对乙烯分子结构和在D2h(M)分子对称群下乙烯分子对称性的考虑，他们构筑了含有微扰ħV的分子系统的哈密顿量和相应的分子波函数，从而具体计算了这些能级对间的微弱相互作用势及其混合引起的B2u和B3u核自旋变体间的相互转换率。

对于B2u和B3u核自旋变体间的转换，计算发现有如表V所示的五个相近能级对µ和µ′能产生较大的微弱相互作用势，它们对引起转换率有较大贡献。表中转动能级态µ用量子数组合(p,J,K)表示，其中J和K分别为转动角动量量子数及其在分子轴上的投影的绝对值；p是值为1或0的量子数。B2u和B3u核自旋变体间的核自旋–核自旋相互作用矩阵元的选择定则为|J′−J|≤2，J′+J≥2，K′−K=±1；核自旋–转动间相互作用矩阵元的选择定则为|J′−J|≤1，J′+J≥1，K′−K=±1。

若假定 B2u和 B3u核自旋变体的各能级间的压力展宽系数的平均值为它们之间的压力展宽系数，即Γµµ′=(Γµµ+Γµ′µ′)/2，进一步取其与气压的正比例系数Γµµ′/p=Γ/p为实验测量值 30 MHz/Torr[75]并引入态混合强度Faa′，根据量子弛豫理论可将B2u和B3u核自旋变体间的转换率简化为[70,74]：

通过将所有转动能级对 (µ,µ′)归类分为近简并能级对 (ν,ν′) 和非简并的能级对 (a,a′)，计算中对µµ′的求和可更换为对νν′和对aa′的归类求和。由上述过程计算得到的相关结果分别列于表 V中。从表中最后一栏知道B2u和B3u核自旋变体间的转换率在气压 1 Torr时的计算结果为 5.2×10−4s−1。我们的实验结果为 (5.5±0.8)×10−4s−1[69]。可见在实验误差范围内理论计算值与实验测量值很接近。这再次表明了量子弛豫效应在乙烯分子的B2u和 B3u核自旋变体间的相互转换过程中的主导作用。从表 V中的计算结果还可看出，能级在898.886 cm−1附近的能级对 (p,J,K)−(p′,J′,K′)=(1,21,11)−(1,23.10)只有核自旋–核自旋相互作用，因它不符合核自旋–转动相互作用的量子数选择定则而没有核自旋–转动相互作用。前者的核自旋–自旋相互作用对转换率有94%的贡献，可见其它能级对对核自旋–转动相互作用和对转换率的贡献相对较小。我们期待正在进行的对核自旋–转动相互作用的分析能给出其产生的转换率的具体数值，以给出乙烯分子在量子弛豫过程中进行核自旋变体间转换的完整物理图像。

考虑转动量子数J小于48且其能级间隔小于90 GHz所有转动能级对的贡献，根据(7)式，可以得到乙烯分子B2u和B3u核自旋变体间的转换率随乙烯气压变化的关系。当乙烯气压p=760 Torr时B2u和B3u核自旋变体间的转换率的计算值为 11.8×10−4s−1。图16给出了室温295 K下B2u和B3u核自旋变体间的转换率在1个大气压力内的复杂变化关系图[70]。在小于10 Torr的气压下，正如实验中所观测到的那样，该转换率随压力直线变化；当压力为10到50 Torr之间时，转换率随气压的升高而减小；当压力在50到760 Torr之间变化时，转换率随气压而上升，在235 Torr达到极大值后随气压升高又缓慢减小。

图16.室温295 K下B2u和B3u核自旋变体间的转换率随乙烯气压变化的关系图[70]。

V.总结和展望

本文从核放射性衰变的三种放射线和原子的核式结构模型出发自然地引入了原子核的构成问题。接着以学术事件的发展年代为时序，首先较详细地综述了质子的发现和中子的发现以及公认原子核由质子和中子组成的科学简史，总结了质子和中子以及其它近三十种原子核的核自旋与核自旋磁矩。之后，以核自旋为主线，提出了分子的核自旋变体的概念，具体讨论了氢分子的两种核自旋变体和乙烯分子的四种核自旋变体。文章侧重于对乙烯分子的核自旋变体的分离和转换的实验和理论研究的全面介绍，着重概述了将乙烯分子的一种核自旋变体与其它种分离开的光诱导漂移实验方案与基本实验原理；全面介绍了用宇称守恒和态混合理论与量子弛豫理论分别定性和定量解释核自旋变体间相互转换新奇量子现象物理机制的研究结果。

表V.对B2u和B3u核自旋变体间的相互转换最重要的五组乙烯分子转动能级对[70]。第2栏是(p′,J′,K′)的能级值；第3栏表示的能级差是 (p,J,K)的能级减去 (p′,J′,K′)的能级。

我们首次研究了具有四种核自旋变体的乙烯分子的核自旋变体的分离与转换，这是该研究领域迄今为止对有多种核自旋变体气相分子的唯一实验研究结果。在我们的研究中，用10P(44)CO2激光把乙烯的B2u核自旋变体分离了开来。当气压为1 Torr，在3分钟内可将其浓度减弱到其自然状态下的3%。B2u与B3u核自旋变体间能够相互转换，它们间的转换率与气体压力的依赖关系为 [(5.5±0.8)×p+(1.8±1.3)]×10−4s−1，这个转换率要比B2u与Ag间、或比B3u与Ag核自旋变体间的转换率大得多。我们用宇称守恒和量子弛豫理论定量地解释了乙烯分子四种核自旋变体间相互转换的观测结果。我们的结果为乙烯分子的核自旋变体间存在着弱相互作用提供了实验依据。实验信息和结果为乙烯分子的核自旋变体的科学研究和实际应用提供了宝贵的实验数据。

最新研究证明[76]，用仲氢使乙炔(C2H2)催化加氢的化学合成方法能提高乙烯分子的核自旋变体浓度；将其应用于分子的核磁共振信号观测，浓度改变后的乙烯分子核自旋变体能明显增强其核磁共振(NMR)信号强度。像氢分子那样有正氢和仲氢，乙炔分子也有两种核自旋变体，正乙炔(I=1)和仲乙炔(I=0)。平常乙炔分子中正乙炔与仲乙炔的成份混合比为3比1。当乙炔与仲氢的混合物连续不断地流过Pd/TiO2催化剂时，在该催化剂表面上炔烃和烯烃的催化加氢某种程度上以成对氢的方式进行，也就是说，在化学反应形成乙烯分子的过程中，仲氢(I=0)中的两个H原子能保持它们核自旋反平行的状态和相关性。仲氢可以添加到乙烯分子同边和对边上的两个氢原子位置上，分别形成Z-型和E-型乙烯分子。因此，平常乙炔与仲氢的合成物乙烯中没有I=2的核自旋变体产生，从而引起其它核自旋变体成份比的增加及其浓度的增强。针对B2u与B3u核自旋变体间的转换率，该文用化学合成方法浓缩乙烯分子核自旋变体的浓度获得了与我们用光诱导漂移技术一致的测量结果，并对1个大气压下乙烯核自旋变体的转换进行了观测。同时，该文的应用结果表明[76]:1)分子的核自旋变体浓度的增强可用浓缩了的另一种分子的核自旋变体通过化学合成方法获得；2)除了氢气之外，浓度提高后的其它分子的核自旋变体也会增强其核磁共振信号。

核自旋变体是分子的基本存在形式，这是遵循量子力学中全同性原理对描写全同性粒子体系的状态波函数对称性要求的必然结果。虽然人们很早就开始了对氢分子的核自旋变体的研究和认识，然而，由于分离实验手段的限制，人们对于氢气以外的很多其它分子的核自旋变体的认识和知识积累都很有限。现行的教科书除了对双原子氢分子的核自旋变体正氢和仲氢有描述外，很难找到其中有关其它多原子分子的核自旋变体的知识。对多原子分子核自旋变体的分离和转换的实验研究还正处在起步阶段，需要大量的原创性实验和理论工作去拓展和丰富它。任何实验信息和结果都将填补该领域的知识空白和为各相关学科（例如分子科学和量子力学及量子化学等）的发展提供基本的实验依据；研究结果也会有重要的实践意义，因为浓度改变后的核自旋变体的相互转换将影响分子的NMR和核磁共振成像(MRI)信号强度。

致 谢

本文工作得到Profs.K.Takagi,Y.Moriwaki,F.Matsushima,P.L.Chapovsky,R.M.Lees,T.Oka,J.T.Hougen,K.Uehara的指导及课题组成员的帮助，在此一并表示衷心地感谢。作者感谢国家自然科学基金 (91536105，11174186，11074147)和 “天山学者计划”与日本学术振兴会 JSPS(P04063，L10519，BR161302)的资助。

参考文献

[1]Becquerel H.Compt.Rend.,1896,122:420-421

[2]Becquerel H.Compt.Rend.,1896,122:501-503

[3]Curie P,Curie M.Compt.Rend.,1899,129:714-716

[4]Rutherford E.Phil.Mag.Series 5,1900,49:1-14

[5]Rutherford E.Phil.Mag.Series 5,1900,49:161-162

[6]Radvanyi P.Eur.Phys.J.H,2013,38(4):433–441

[7]Rutherford E.Phil.Mag.Series 5,1899,47:109-163

[8]Villard P.Compt.Rend.,1900,130:1010-1012

[9]Villard P.Compt.Rend.,1900,130:1178-1179

[10]Rutherford E.Phil.Mag.,1903,5:177-187

[11]Rutherford E,Soddy F.Phil.Mag.,1902,4:370-396

[12]Rutherford E,Soddy F.Phil.Mag.,1903,5:576-591

[13]Ramsay W,Soddy F.Proc.Roy.Soc.London,1903 72:204-207

[14]Chadwick J.Verhandlungen der Deutschen Physikalischen Gesellschaft,1914,16:383–391

[15]Brown L M.Physics Today,1978,31(9):23-28

[16]Rutherford E.Phil.Mag.,1911,21:669-688

[17]Geiger H,Marsden E.Roy.Soc.Proc,A,1909,82:495-500

[18]Barkla C G.Phil.Mag.,1911,21:648-652

[19]Van den Broek A.Nature,1911,87:78-78

[20]Van den Broek A.Nature,1913,92:372-373

[21]Van den Broek A.Nature,1913,92:476-478

[22]Van den Broek A.Nature,1914,93:7-8

[23]Moseley H G J.Phil.Mag.,1913,26:1024-1034

[24]Moseley H G J.Phil.Mag.,1914,27:703-713

[25]Bohr N.,Phil.Mag.,1913,26:1-24

[26]Bohr N.,Phil.Mag.,1913,26:476-502

[27]Bohr N.,Phil.Mag.,1913,26:857-875

[28]Chadwick J.Phil.Mag.,1920,40:734-746

[29]Rutherford E.Phil.Mag.,1914,27(159):488-498

[30]Rutherford E,Nuttall J M.Phil.Mag.,1913,26:702-712

[31]Prout W.Annals.of Philosophy,1815,6:321–330

[32]Darwin C G.Phil.Mag.,1913,25:201-210

[33]Darwin C G.Phil.Mag.,1914,27:499-506

[34]Marsden E.Phil.Mag.,1914,27:824-830

[35]Rutherford E.Phil.Mag.,1919,37:538-571

[36]Rutherford E.Phil.Mag.,1919,37:581-587

[37]RutherfordE.Proc.Roy.Soc.London A,1920,97(686):374-400

[38]Rutherford E,Chadwick J.Phil.Mag.,1921,42:809-825

[39]Blackett P M S,Lees D S.Proc.Roy.Soc.London A,1932,136:325-338

[40]Dennison D M.Proc.Roy.Soc.London A,1927,115(771):483-486

[41]Sun Z–D.Chinese Science Bulletin,2016,61(22):2429-2440

[42]Glasson J L.Phil.Mag.,1921,42(6):596-600

[43]RobertsJK.Proc.Roy.Soc.London A,1922,102(714):72-88

[44]White J W,White A B.Aust.J.Chem.,2011,64(7):855–863

[45]Bothe W,Becker H.Z.Phys.,1930,66(5-6):289-306

[46]Curie I,Joliot F.Compt.Rend.,1928,186:1722-1724

[47]Curie I,Joliot F.Compt.Rend.,1928,187:43-45

[48]Curie I,Joliot F.Compt.Rend.,1932,194:273-275

[49]Chadwick J.Proc.Roy.Soc.,1932,136(830):692-708

[50]Chadwick J.Nature,1932,129:312-312

[51]Anderson C D.Phys.Rev.,1933,43(6):491–494

[52]Joliot F,Curie I.Nature,1934,133:201-202

[53]Curie J,Joloit F.Nature,1934,133:721-721

[54]Chadwick J,Goldhaber M.Nature,1934,134:237-238

[55]Heitler W,Herzberg G.Naturwissenschaften,1929,17(34):673-674

[56]Iwanenko D.Nature,l932,129:798-798

[57]Bacher R F,Condon E U.Phys.Rev.,1932,41:683-685

[58]Heisenberg W.Z.Phys.,1932,77:1-11

[59]Heisenberg W.Z.Phys.,1932,78:156-164

[60]Heisenberg W.Z.Phys.,1933,80:587-596

[61]Fermi E.Z.Phys.,1934,88(3-4):161-177

[62]Wang K C.Phys.Rev.,1942,61(1-2):97-97

[63]Davis R.Phys.Rev.,1952,66(6):976-985

[64]Cowan C L,Reines F,Harrison F B,Kruse H W,M-cGuire A D.Science,1956,124:103-104

[65]Bonhoeあer K F,Harteck P.Die Naturwissenschaften,1929,17:182-182

[66]Landau L D,Lifshitz E M.Quantum Mechanics,Pergamon,Oxford,3rd ed.,1981

[67]Herzberg G.Molecular Spectra and Molecular Structure.II.Infrared and Raman Spectra of Polyatomic Molecules,Van Nostrand Reinhold,New York,1945

[68]Hougen J T,Oka T.Science,2005,310:1913-1914

[69]Sun Z-D,Takagi K,Matsushima F.Science,2005,310:1938-1941

[70]Chapovsky P L,Zhivonitko V V,Koptyug I V.J.Phys.Chem.A,2013,117:9673-9683

[71]Bunker P R,Jensen P.Molecular Symmetry and Spectroscopy,2nd ed.,NRC-CNRC:NRC Research Press,Ottawa,1998

[72]Gel’mukhanov F K,Shalagin A M.JETP Lett.,1979,29:711-713

[73]Curl R F,Kasper J V V,Pitzer K S.J.Chem.Phys.,1967,46:3220-3228

[74]Chapovsky P L.Phys.Rev.A,1991,43:3624-3630

[75]Blanquet G,Bouanich J-P,Walrand J,Lepere M.J.Mol.Spectrosc.,2003,222:284-290

[76]Zhivonitko V V,Kovtunov K V,Chapovsky P L,Koptyug I V.Angew.Chem.Int.Ed.,2013,52:13251-13255

Nuclear spin and progresses in study on separation and conversion dynamics of nuclear spin isomers of ethylene

Sun Zhen-Dong,Ma Li-Sha
School of Physics,Shandong University,Jinan 250100;School of Physics and Electrical Engineering,Kashgar University,Kashi 844006,P.R.China

The nucleus is composed of protons and neutrons.The total angular momentum of the protons and neutrons in an atomic nucleus is usually referred to as nuclear spin.Nuclear spin isomers and their stability are fundamental concepts in quantum mechanics,and all molecules possessing identical nuclei with nonzero spin have two or more distinct nuclear spin isomers with diあerent arrangements of total nuclear spin quantum numbers.Thus,researchers have tried to separate the nuclear spin isomers of gaseous polyatomic molecules and study the conversion mechanisms among them for many years.However,the studies in this fi eld did not make progress until the early 90s.In 2005,we made a study on the separation and conversion of nuclear spin isomers of ethylene for the fi rst time,to which we gave a special introduction in this paper.Firstly,the scienti fi c history about the discovery of the protons and neutrons that form nucleus is brie fl y described chronologically;the concept of nuclear spin isomers is presented,and the nuclear spin isomers of hydrogen and ethylene molecules aref described in detail.Secondly,we give a full description of the progresses made in the experimental study on the separating the nuclear spin isomers of gaseous ethylene with light-induced drift technique,and make a quantitative explanation on the interconversion dynamics among the nuclear spin isomers of ethylene based on parity conservation and quantum relaxation theory.Finally,we brie fl y summarize the latest research fi nding.The enrichment of the nuclear spin isomers of ethylene can be achieved through chemical synthesis using the acetylene catalytically hydrogenated with para-hydrogen,which would suきciently and successfully enhance nuclear magnetic resonance signal.

the proton;the neutron;nuclear constitution of atoms;nuclear spin isomers;separation and conversion rate of nuclear spin isomers;light-induced drift;quantum relaxation;parity conservation;ethylene;precision laser spectrum;nuclear magnetic resonance

O621.13

A

10.13725/j.cnki.pip.2017.06.001

1000-0542(2017)06-0193-23

*E-mail:zdsun@sdu.edu.cn

date:2017-08-07