一种水下声成像算法研究及扩展

作者/廖鹏，中国船舶重工集团公司第七一〇研究所

一种水下声成像算法研究及扩展

作者/廖鹏，中国船舶重工集团公司第七一〇研究所

本文阐述了水下声成像的基本原理与研究的重要意义，利用Kraken简正波模型进行了水下声场传播模型的仿真，分析了水中声波在距离上和深度上的衰减情况。推导了一种三阵元水听器系统的成像方法并给出了仿真结果，最后将算法由二维成像扩展到三维成像。

水下声成像；Kraken简正波模型；三维成像

引言

水下声成像是声成像的一个分支，在水声探测中有着重要的作用，通过物体对声波的后向散射作用进行水下定位，逐点画图成像。利用声波进行成像，是在声纳测距与测向的基础上发展而来的。声纳测距主要是利用接收回波与发射脉冲信号间的时间差，计算出目标的距离；声纳测向主要是利用回波到达由多个换能器组成的水听器系统的声程差和相位差，计算出目标的方位。

在水下声成像中，基本的声成像技术有三种：声透镜技术、波束形成技术、声全息技术。这三种声成像方法都使用相同的操作：空间处理（从声场中得到图像）、换能（将声能转换成电能）、检波（将高频信号转换成可观测且接近直流的图像信号）、显示（以某种形式显示为图像）。这三种方法的不同之处在于对这些操作进行的先后顺序的不同。

本文使用的是一种与以上三种均不同的新的声成像方法。三个换能器的空间位置形成各自距离相等正三角形，组成一个水听器系统。利用回波信号到其中两个等效阵元之间的相位差、时间差和振幅差值，测定各个目标点的距离与方位。

1.水下声场仿真

目前用于计算浅海混响的理论模型主要有射线模型、简正波模型，本文使用简正波模型进行水下声场仿真。利用简正波模型来计算水下混响的基本思想最早由Bucker和Morris于1968年提出，简正波混响模型用数学公式描述为：

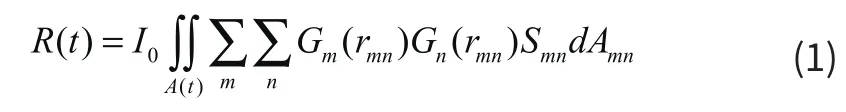
其中，R(t)是t时刻的混响强度，I0是持续时间为τ0的声源强度，Gm是指经路径m从声源到散射元dA的传播。Gn是指经路径n从散射元dA到接收器的传播。Smn是指单位区域对入射路径m外向路径n的散射，rmn是指从声源或接收器到散射元dA的距离，dA基本的散射区域。求和是相对于连接声源与接收器和散射元的所有路径（射线或模态）。积分是相对于t时刻对混响有贡献的所有散射区域。

水下声场仿真主要由三部分组成，分别为目标亮点回波信号产生、前置预处理和后置处理。

（1）目标亮点回波产生：主动发射一个载频信号，经信道传输，由反射点时延、相位时延形成反射后的回波信号，总目标反射的回波信号实际上是由目标亮点回波的相干叠加合成。

（2）前置预处理：完成对信号的预处理，为后续波束形成和图像生成提供可靠的数据，功能主要包括对仿真信号的采用、高频带通滤波器、正交解调、低通滤波和低频抽取等。

（3）后置处理：完成前置预处理后仿真信号的复数字波束形成，对目标方位、距离、强度等信息进行估计，再利用图像色彩显示控制技术最终生成瞬态回波图像，即目标二维亮点强度分布区。

图1 浅海声速剖面图

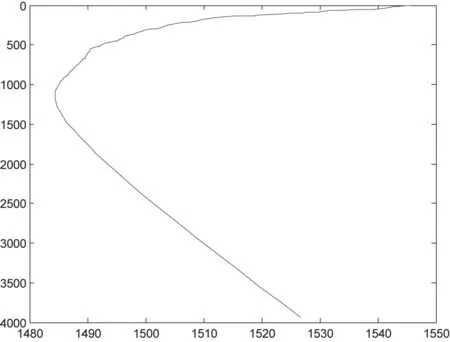
图2 深海声速剖面图

海洋中的平均声速近似等于1500m/s，声速随温度、盐度、压力的增加而增加，其中以温度的影响最显著。声速在海中的声速剖面图如图1和图2所示。图1表示的是浅海（0～250米）的声速剖面图，图2表示的是深海（0～4000米）的声速剖面图。在浅海，海洋表面受到阳光照射时水温较高，声速随着深度增加而降低，呈现声速负梯度；在深海，水温比较低而且稳定，声速随着深度的增加而增加，呈现海洋内部的声速正梯度。

根据浅海的声速梯度分布，利用Kraken简正波模型对浅海水下声传播进行仿真。声速剖面图如图1所示，假设海面为3级海况，水深为250m，声源频率为500Hz，声源深度为60m，海水密度为1.03g/cm2，吸收系数等于0.15dB/kmHz。声场仿真图如下图3所示。

图3 浅海水下声场仿真图

图3的左边的图表示声波在深度和距离上的传播损失，右图表示的是在深度60m处，即声源位置处开始，声波随距离的衰减趋势。由图3可以看出，越靠近声源的位置声强越大，但是水下声传播过程中的衰减并不是线性的。

声场中任意点的声压公式为：

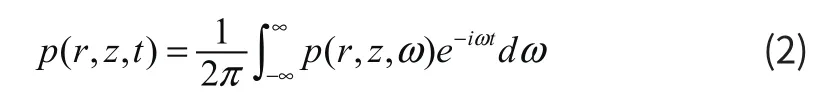
且p(r,z, ω) =S(ω)g(r,z,ξ)，上式可化为：

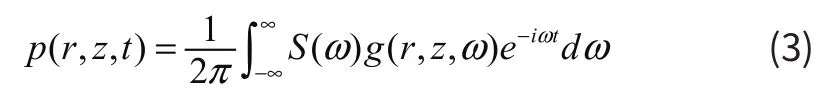
其中，S(ω)为声源信号，g(r,z,ω)为声场的传播函数。

2.声成像算法研究

本文假设的声纳系统共有三个收发合制的换能器，三个换能器的空间位置成正三角形，同时接收各个方向上的回波信号。DDS信号发生器产生22kHz～24kHz的线性调频信号LFM，经过三个发射换能器轮流向水中或者空气中发射出去。三个换能器的空间位置是相互固定的，它们理论上可以根据接收到的回波信号确定空间任一点的位置。下面以平面内两个换能器确定平面内任意一点为例，建立理想情况下的声传播模型（即认为声在介质中的传播路径是一条直线）。图4为平面内信号的收发模型。

图4 平面内两换能器收发信号模型

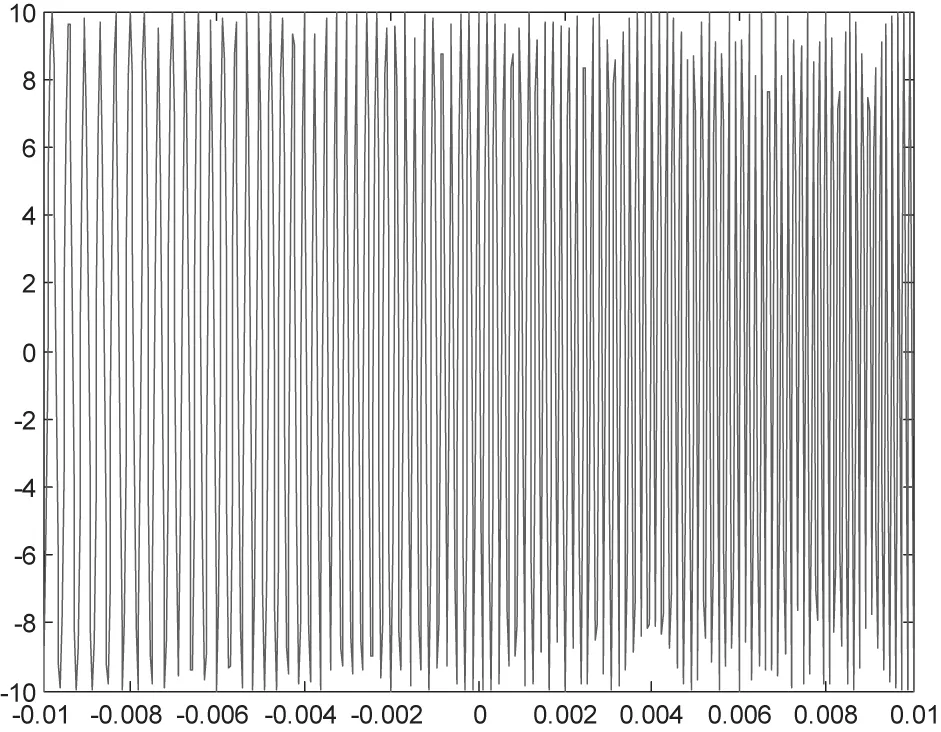
图5 线性调频信号

换能器A、B发射的信号为线性调频信号，表达式如下：

图5为此线性调频信号在MATLAB下的波形图。公式中信噪比SNR=10，载波频率fc=5kHz，带宽B=5kHz，线性调频信号脉冲宽度TP=0.01s（只发射一段时间很短的脉冲），采样频率fs=30kHz。在已有发射信号LFM的基础上产生的回波信号，可以表达为在原信号的基础上叠加其延时衰减的分量。假设只有一个回声的情况下，可简化其模型为：

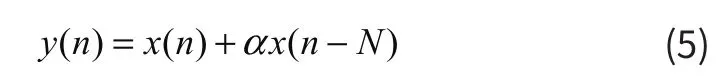
其中α为反射系数，N为延迟时间。为了简化计算，假设平面一共有10个点，换能器A、B的间距为1个单位，水平面的长度和高度均为10个单位，换能器发射的信号传播至每个点上都会产生不同时延的回波，每个换能器接收到的总的回波信号为各个点的回波信号的总和，表达式为：

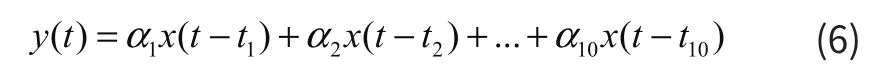
所以，LMF信号在每个点处的回波模型可以表达为：

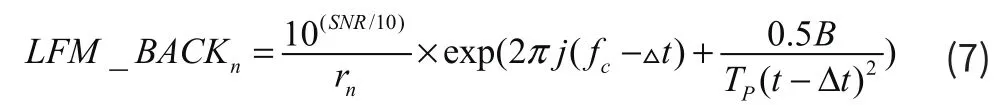
rn为点到换能器的直线距离，▵t为每个回波信号的时延。换能器接收到的总的回波信号表达式为：

对回波信号进行自相关运算后得到的函数存在一些极值点，根据相关函数的定义我们知道，这些极值点就原信号自相关、原信号与回波信号互相关、回波信号与原信号互相关的相关函数值，根据这些点的相对位置、采样频率和声速，就可以确定反射点的位置了。

在MATLAB仿真中，对发射信号加窗处理后，与接收到的信号进行卷积，得到的图形的波峰位置处就是信号的相关函数值。

图6表示的是换能器A和B各自的发射信号与接收信号进行卷积运算的结果，同一个目标点在两个换能器中形成的波峰位置不同，根据两个换能器中波峰点的相对位置与采样频率的大小，通过交叉运算就可以计算出目标点的位置坐标。图7表示的是对10个目标点方位估计的仿真结果。

由仿真可以看到，两个换能器就可以确定平面内任意点的位置。拓展到三维空间中，则三个换能器理论上就可以确定空间任一点的位置。在具体的实验中，首先利用三个换能器中的两个画出一系列二维图像，在将这些图像拼接成一个完整的三维图像。

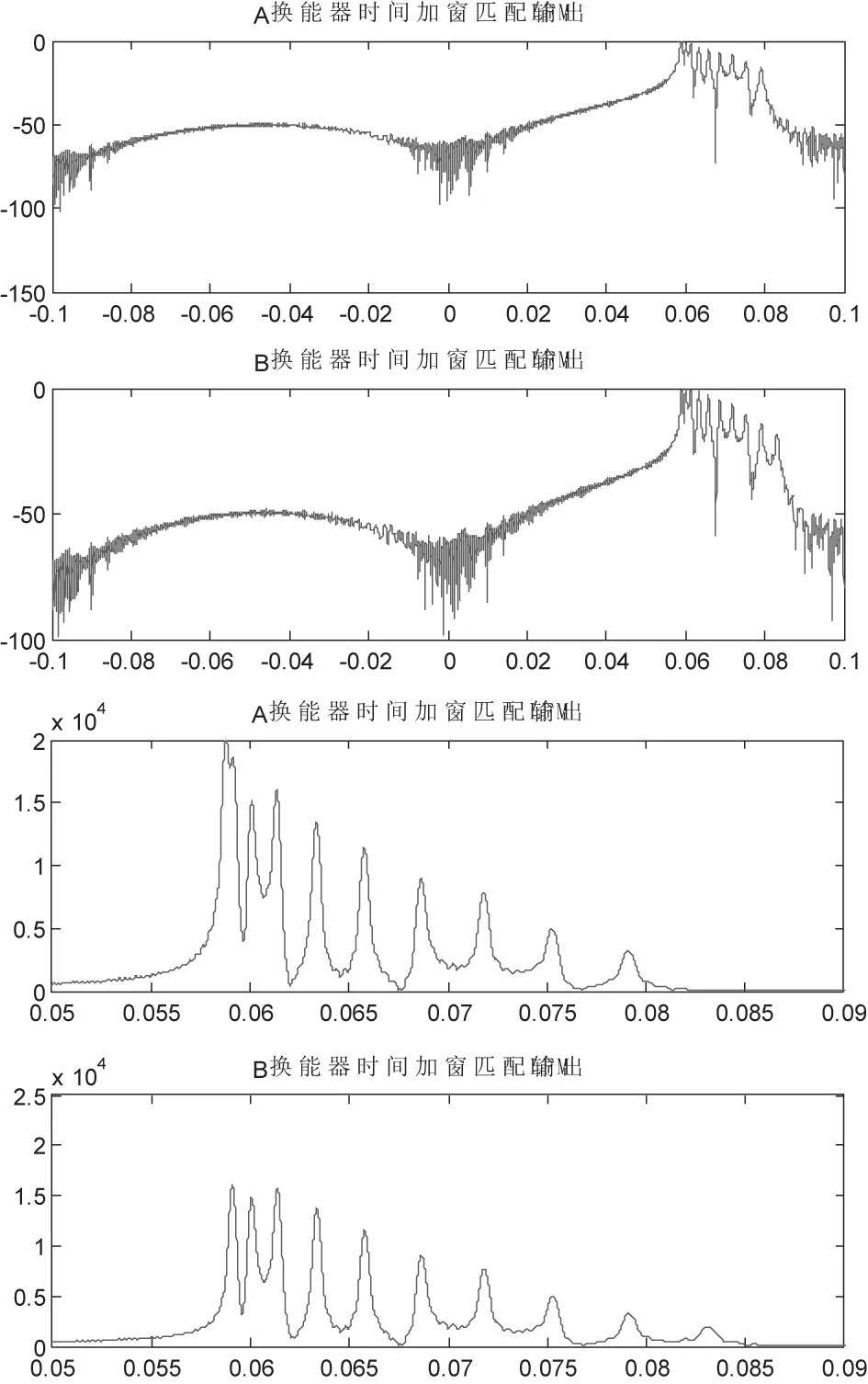
图6 发射信号与回波信号的卷积运算结果

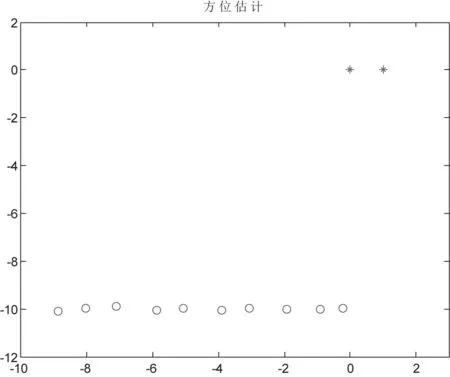
图7 目标点的方位估计

3.声成像算法扩展

上文建立了一个理想的信号模型，利用两个换能器画出了平面内10个目标点的位置，但是在复杂的环境中，由于目标点数非常的多，回波信号所含的信息量非常巨大，这种算法效果并不好。

图8 信号的发射与接收

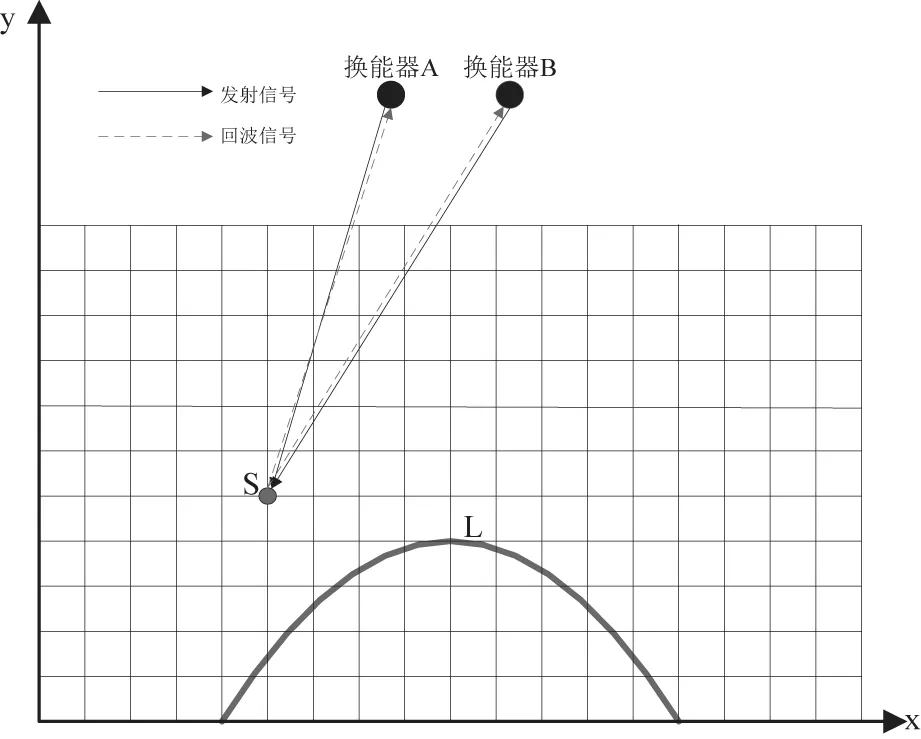
图9 逐行扫描信号模型

图8表示的是信号的发射与接收波形示意图，发射换能器发射的信号经过一段时间后回来，换能器A与换能器B接收到的回波信号前沿的时延分别为T1、T2。由于两个换能器的位置不同，接收到的信号也就不同，所以理论上可以利用两个换能器接收到的信号差异确定目标的方位。

在这里用逐点逐行扫描的方法确定空间点的位置。如图9所示，以平面内两个换能器A、B为例，目标物体为L，利用这两个换能器画出L的平面图。建立平面坐标系，将换能器前方的区域用网格划分为一系列的点，进行逐点扫描。

首先建立网格中任一点的声信号模型。换能器发射信号为x(t)，是一段短脉冲，采用假设法，假设在S点出有目标点，回波信号为y(t)。利用基于滑动窗口的快速傅立叶变换进行归一化互相关匹配，采用滑动窗和快速傅立叶变换（FFT）与反变换（IFFT）对归一化互相关系数进行计算，公式如下：

其中u= 0,1,...M-1，M为回波信号总长度。用x(t-u)代表标准波形在t-u位置上的幅度值，x是标准波形序列x(t-u)的平均幅度值，yu(t)代表查找区域上以第u个位置为起点的与标准波形同样长度区域内的幅度值序列，yu则是此序列的平均幅度值。r(u)构成了一个相关序列，序列上的点均位于[-1，+1]区间内，+1意味着两个波形之间具有完全匹配的正向线性关系，-1意味着两个波形之间具有完全匹配的反向线性关系，在匹配位置将出现峰值，峰值接近于1。

根据两个换能器接收到的回波信号与发射信号的相关性，大致可以确定假设点S是否存在。如果假设点存在，则匹配滤波的相关性强，峰值明显，否则假设点就不存在，继续查找下一点。图中只有目标L才能反射回波信号，所以只有在L处匹配滤波相关性最强。平面目标方位估计仿真如图10所示。

图10 平面目标点的方位估计

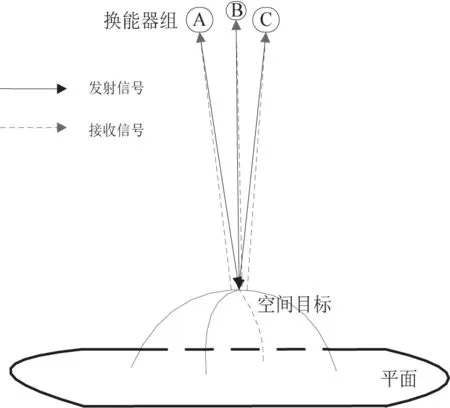
图11 空间方位估计模型

扩展到空间内，空间方位估计模型如图11所示。和平面目标方位估计一样，以三个换能器中的两个确定某一平面内的目标点的坐标，将产生的一系列平面内的点结合起来，形成一个完整的三维图像。

4.结论

本文阐述了水下声成像的基本原理与研究的重要意义，推导了一种三基阵元水听器系统的声成像算法。利用Kraken简正波模型，进行了水下声场仿真，并在此基础上建立了水下声信号的信号模型。利用声信号的理想模型，通过MATLAB软件进行了仿真，成功实现了平面内的目标成像，并扩展到三维空间中成像。

* [1]田坦，刘国枝，孙大军．声纳技术[M].哈尔滨工程大学出版社，2000

* [2]刘伯胜, 雷家煜主编．水声学原理[M]．哈尔滨工程大学出版社，1993.12

* [3]唐利娜，孙大军．水下三维成像及声纳图像处理技术研究[D].哈尔滨工程大学硕士学位论文，2009

* [4]Lee C.-C., Lee J.-H., Robust adaptive array beamforming under steering vector sensors. IEEE Trans．Antennas propaga te，1997

* [5]Alex B. Gershman, Nicholas D. Sidiropoulos. Convex optimization-based beamforming．IEEE Signal Processing Magazine，2010