随机二人零和微分博弈

张芬1，吴红星1，骆雯琦1，周富磊

(1.上饶师范学院 数学与计算机科学学院,江西 上饶 334001；2.上饶中学,江西 上饶 334000)

随机二人零和微分博弈

张芬1，吴红星1，骆雯琦1，周富磊2

(1.上饶师范学院 数学与计算机科学学院,江西 上饶 334001；2.上饶中学,江西 上饶 334000)

利用最优控制理论来分析随机条件下的二人微分博弈问题。首先，给出随机微分方程和性能指标函数；然后，引出了相应的随机二人零和微分博弈问题；最后，通过Q-Riccati微分方程来得到随机微分博弈的最优闭环表达式和性能指标函数表达式。

最优控制；博弈；随机微分方程；Q-Riccati方程

Fleming研究了一般条件下的随机零和微分博弈问题，并得到相应值函数的存在性，这为研究随机零和微分博弈问题建立了基础[1]。潘立平利用Q-Riccati微分方程研究无限维最优控制问题，得出可以用有限维的最优控制问题解来逼近相应无限维的最优控制问题解[2]。Elliott研究了随机微分博弈最优控制策略和鞍点策略的存在性[3]。朱怀念通过Riccati微分方程和It积分研究了不定仿线性二人零和微分博弈问题，并给出了最优可行决策的显示表达式，且进一步得到了最优性能指标函数的表达式以及其存在的充分必要条件[4]。尤云程利用Q-Riccati方程研究了确定性情况下的二人零和微分博弈[5]。王源昌通过Q-Riccati微分方程给出了非自治二人零和微分博弈的最优控制解[6]。这些结果为本文的研究奠定了基础。

1 问题描述

本文主要讨论在时间区域0,T(T>0)中的随机二人零和微分博弈。定义0,y0∈0,T×Rn(0为初始时间，y0为初始状态)，并给出相应的随机状态方程如下：

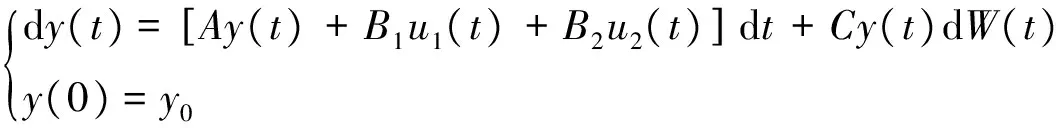
(1)

其中y(·)∈Rn，矩阵A,C∈Rn×n，B1,B2∈Rn×k，函数u1(t)，u2(t)∈Rk,Y=L2(0,T;Rn),Yc=C([0,T];Rn),U1=L2(0,T;Rk)以及U2=L2(0,T;Rk)定义成所需的空间，将所有的策略u,v∈U1×U2称之为可行策略。且其性能指标函数[7]形式如下：

(2)

定义h(·):Rn→R，并将h(y(T))定义为C2(Rn)函数，同时设R1是n×n阶正定矩阵，R2是n×n阶负定矩阵。

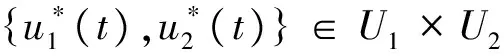
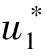
(3)

为了解决此问题，现引进Q-Riccati微分方程：

(4)

其中，Q-Riccati的解P(t,y):0,T×Rn是一个非线性的映射。Pt(t,y)和Py(t,y)分别表示关于P(t,y)对t和y求偏导。且Q-Riccati微分方程式(4)的解满足下面的定义。

定义1[5-6]设P(t,y)是Q-Riccati微分方程式(4)的一个正规解，并满足下面的条件：

(1)P(t,y)关于(t,y)连续，并且P(t,y)分别对t和y是连续可微；

(2)对于∀t∈0,T，P(t,·):Rn→Rn为梯度算子；

(5)

关于任意给定的y0∈Rn，式(5)必只存在一个全局解y∈Yc。

令P(t,y)为微分方程式(4)的正规解，则根据P(t,y)的定义可知：对于∀t∈0,T，∃P(t,y)的不定积分φ(t,y)，其中φ(t,y):0,T×Rn是一个非线性函数且满足下式：

(6)

引理设y(·)是初始值为y0和可行策略u1(·),u2(·)的状态轨迹方程。如果P(t,y)是微分方程式(4)的正规解，且φ(t,y)是P(t,y)的一个不定积分，则φ(·,y(·))在时间域0,T上是绝对连续函数的，也既φ(·,y(·))∈AC0,T;R。

2 主要结果

定理1 设y(·)是关于初始值取y0和可行策略u1(·),u2(·)状态轨迹方程。当P(t,y)是式(4)的一个正规解时，则∃P(t,y)的不定积分φ(t,y)，且φ(·,y(·))∈AC0,T;R，使得对a.e.的t∈0,T成立下式：

证明：由引理可知φ(t,y(t))a.e.关于时间域0,T上的t可微，且成立下式：

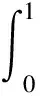
(8)

对式(8)的两边关于t求微分整理可得下式：

其中P(t,y)为对称矩阵，故P(t,y)为自伴算子，所以Py(t,y(t))=Py(t,y(t))'。第三个等式结合方程式(4)便可得到。现对式(9)进行分布计算：

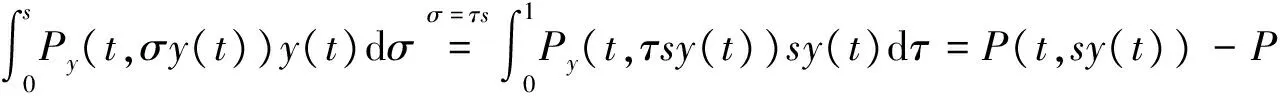
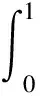
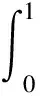
(11)

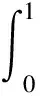
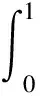
(12)

现在将式(11)和式(12)代入式(9)可得下式：

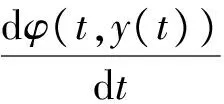
(13)

因此定理1证毕。

定理2[6]设P(t,y)为微分方程式(4)的正规解，则相应的随机二人微分博弈问题可解，其最优策略和性能指标函数值形式如下：

(14)

(15)

并可知式(14)使得式(15)满足不等式(3)。

证明：通过利用闭环表示定理和“配方法”来证定理2。根据定理1可得P(t,y)为式(4)的一个正规解，现由Q-Riccati微分方程解的性质可知：P(t,y)既满足引理又满足定理1。故进一步，结合式(2)和式(13)便得下式：

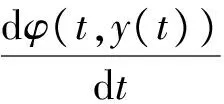
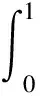
(16)

现引进一个α(t,y(t))函数，且其定义如下：

(17)

由式(17)可得下式：

(18)

所以将式(18)代入式(16)整理可得：

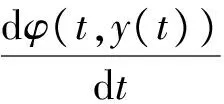
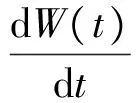
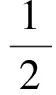
(19)

现对式(19)两边关于t从0到T取积分可得：

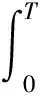
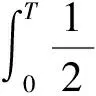
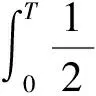
(20)

由式(4)和式(6)可知: 对于任意的y∈Rn，φ(T,y)-φ(T,0)=h(y)-h(0)和φ(T,y)≡h(y)。现将φ(T,y)≡h(y)代入式(20)，对其进行移项整理并取期望整理可得下式：

(21)

因此由式(21)可得：

定理2证毕。

[1] FLEMING W H,SOUGANIDIS P E.On the existence of value functions of two-player zero-sum stochastic differential games[J].Indiana University Mathematics Journal,1989,38(2):293-314.

[2] 潘立平.无限维线性—非二次最优控制问题[J].数学年刊,1997,18(A):93-108.

[3] ELLIOTT R J.The existence of optimal strategies and saddle point in stochastic differentialgames[J].Lecture Notes in Control & Information Sciences,1997,3：123-135.

[4] 朱怀念，张成科，李云龙,等.一类不定仿线性二次型随机微分博弈的鞍点均衡策略[J].广东工业大学学报,2012,290(3):35-39.

[5] YOU Y C.Syntheses of differential games and pseudo-Riccati equations[J].Abstract & Applied Analysis,2002,7(2):61-83.

[6] 张芬,王源昌,雷丹.非自治的二人微分博弈[J].云南师范大学(自然科学版),2014,34(6):8-13.

[7] 雍炯敏,楼红卫.最优控制理论简明教程[M].北京:高等教育出版社,2006.

Random Two-person Zero-sum Differential Games

ZHANG Fen1,WU Hongxing1,LUO Wenqi1,ZHOU Fulei2

(1.School of Mathematics and Computer Science,Shangrao Normal University,Shangrao Jiangxi 334001,China;2.Shangrao Middle School,Shangrao Jiangxi 334000,China)

Using the optimal control theory to analyze that the problem of two-player zero-sum differential game in stochastic situations. First,giving the stochastic differential equation and performance index function;Then,introducing the problem of stochastic two-player zero-sum differential game. Finally,by the Q-Riccati differential equation to obtained the closed-loop expression and the optimal equation of state equation for stochastic differential game.

optimal control；game；stochastic differential equation；Q-Riccati equation

2017-07-04

上饶师范学院自然科学基金资助项目(201724)

张芬(1990-)，女，江西上饶人，助教，硕士，主要研究方向金融数学。E-mail:1024866868@qq.com

O225；O232

A

1004-2237(2017)06-0012-04

10.3969/j.issn.1004-2237.2017.06.003