基于层次分析法与成熟度评价的执法能力评估方法初探1)
黎伟(上海市质量和标准化研究院)刘刚(上海市质量技术监督局)江平(上海市质量和标准化研究院)刘霞 裴会涛(质检总局发展研究中心)
基于层次分析法与成熟度评价的执法能力评估方法初探1)
黎伟(上海市质量和标准化研究院)刘刚(上海市质量技术监督局)江平(上海市质量和标准化研究院)刘霞 裴会涛(质检总局发展研究中心)
执法能力评估可以为提高行政执法效能提供科学依据,是推进依法行政的重要保障。本研究广泛调研现行行政体系下影响执法能力的各相关因素,采用德尔菲专家咨询法,分别从执法人员素质与能力、激励机制、社会共治、保障能力、执法效能五个方面设计了执法能力评估指标体系,并创新性地提出运用层次分析法确定指标权重,并结合成熟度评价方法计算指标得分的总体评估思路,为建立行政执法能力评估方法体系奠定了丰富的理论基础。
行政执法能力 层次分析法 成熟度评价 评估模型
转变政府职能、推进依法行政,是长期以来我国全面深化改革、提高政府管理质量与水平的重要任务。而作为依法行政重要保障的行政执法能力,只有建立在对当前执法水平进行准确评估基础之上,才能不断进行改进和提升。目前,我国针对执法能力评估的研究十分有限,实践中对执法能力主要是采用绩效评估的方式,对指标的评判更多地是依赖专家的主观判断进行定性评估,规范性和严谨性还有待提高。因此,如何有效建立指标体系并确定科学客观的量化评估方法,在当前深化改革的宏观大背景下已经成为当前理论和实践竞相探索的重要课题。
1 执法能力评估指标体系设计
1.1 指标体系构建要点
通过前期对全国多地调研以及上海全市广泛问卷调查,初步梳理出影响执法能力的各主要因素,并在以下原则的指导下,通过德尔菲专家咨询法最终选定评估模型所需的各项指标:
(1)系统性原则。整个指标体系应做到层次结构清晰,同层级指标相互独立,上下级指标间具有一定逻辑关联性。
(2)具体性原则。指标应明确具体,可描述方便理解。
(3)可量化原则。指标应尽可能做到量化为数值,以方便进行测量、比较和量化评估。
(4)可获取原则。指标数据应方便获取。
1.2 指标体系构成要素
基于行政执法的影响因素,结合执法能力的涵义,提出执法能力评估可以采用表1的指标体系进行。执法能力由5个一级指标以及21个二级指标共同构成。一级指标分为执法人员素质与能力、激励机制、社会共治、保障能力、执法效能5个方面,全面评估地方质监行政执法能力的状况。
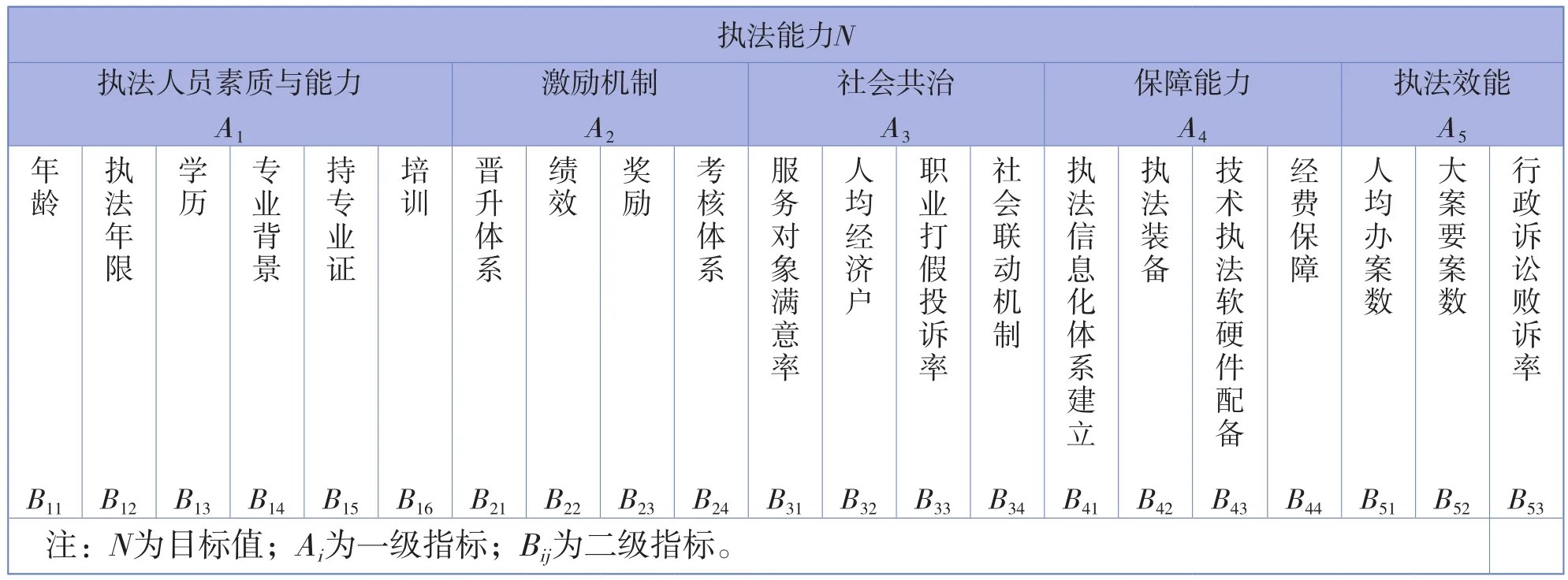
表1 执法能力评估指标体系
2 执法能力指标权重确定——层次分析法
2.1 层次分析法
为了保证评估流程设计的合理性以及评估结果的准确性,科学合理地对执法能力进行评估,本研究在大量文献研究的基础上进行综合比较,最终决定采用层次分析法(Analytic Hierarchy Process,AHP)。AHP最早由美国运筹学家、匹兹堡大学教授T. L. Saaty于20世纪70年代初提出,是一种定性分析与定量分析相结合的综合性评估方法,其总体思路(见图1)基本类似于决策者在对多层次、多因素复杂问题进行分析时的思维过程,最显著优点就在于分层分类对比、系统综合优化。
AHP的基本原理在于,将所要解决的单个复杂问题作为综合系统来对待,按照系统内部各要素(指标)之间的隶属关系,把复杂问题分解转化为条理有序的层次结构,并按上层要素(指标)分类来对同层级要素(指标)构建判断矩阵,两两相较以判断相对重要性,进而计算得出各要素(指标)的权重。后来,Aupetita等人在Saaty的研究基础上又对AHP作了进一步改进,通过引入一致性检验对判断矩阵进行校检,以尽可能减少因专家主观因素而引发与实际情况产生偏差。
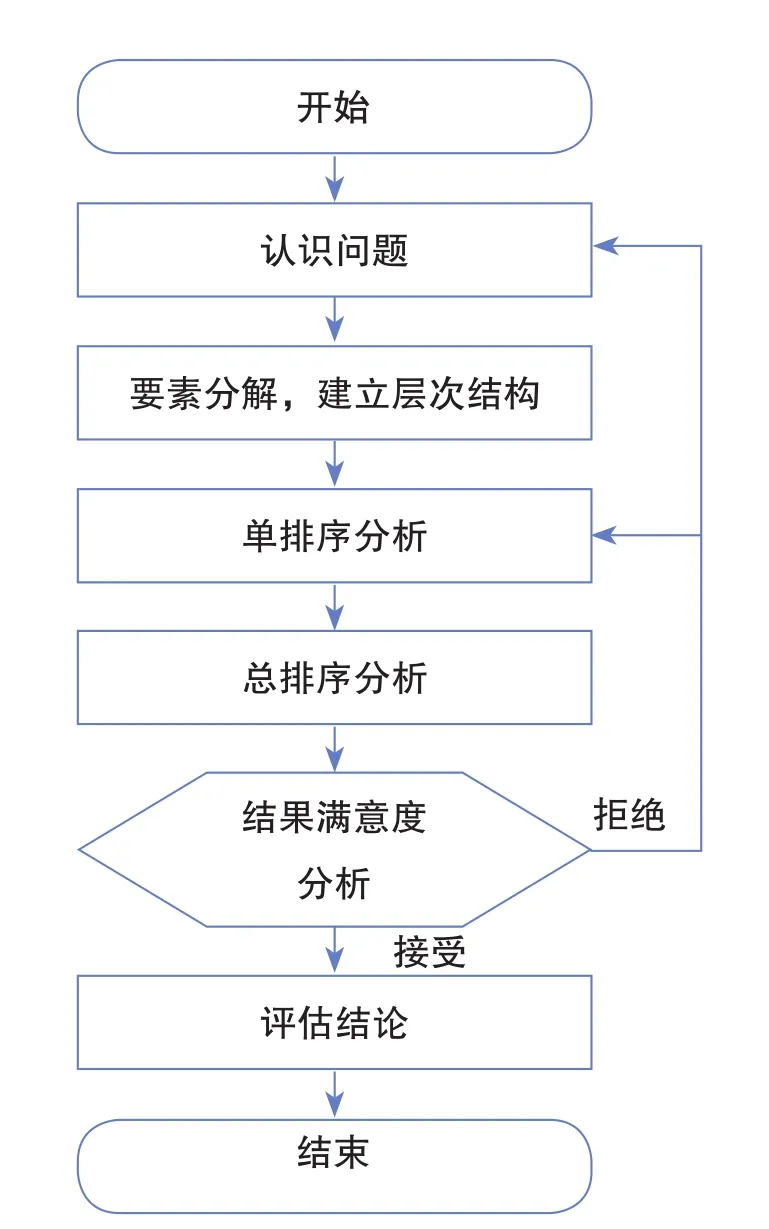
图1 AHP总体思路图
2.2 构建判断矩阵
构建判断矩阵关键在于,设法定量描述出所要比较的要素(指标)就某一目标准则的相对重要性。Saaty等人提出了9级标度法(见表2),并要求按执法能力以及5个一级指标分类,来对其下级指标之间的相对重要性程度进行两两评判(矩阵中需要填写的数值为其所在i行的指标与所在j列的指标两两比较评判的结果,即aij)。

表2 重要性标度含义表
本研究专门邀请了质监、工商、食药监、物价等系统行政执法相关专家及一线执法人员对判断矩阵中指标间重要性程度进行调查,经汇总处理后的判断矩阵调查结果见表3~表8。
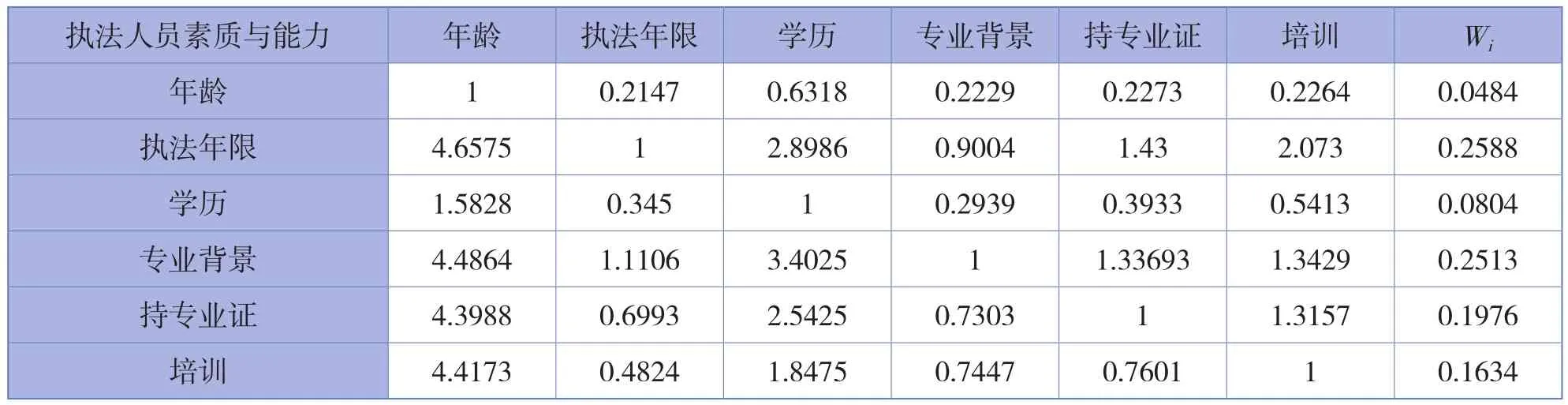
表3 “执法人员素质与能力”的判断矩阵调查结果及权重

表4 “激励机制”的判断矩阵调查结果及权重

表5 “社会共治”的判断矩阵调查结果及权重

表6 “保障能力”的判断矩阵调查结果及权重

表7 “执法效能”的判断矩阵调查结果及权重
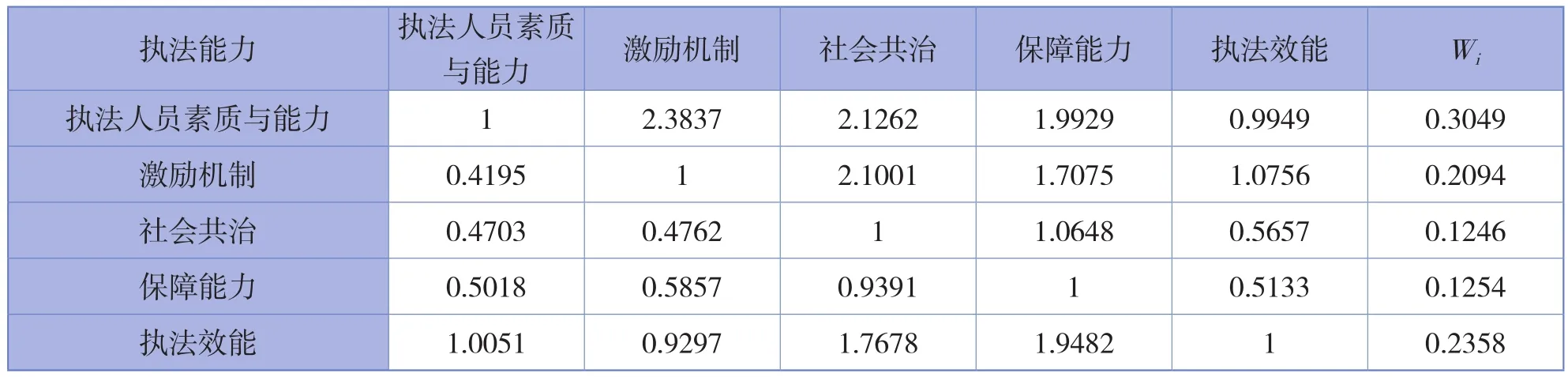
表8 “执法能力”的判断矩阵调查结果及权重
2.3 层次单排序及其一致性检验
2.3.1 层次单排序
根据特征根法计算同一层次判断矩阵中各元素权重并排序,其结果见表3~表8。具体步骤如下:
(1)计算判断矩阵中每一行指标分值的乘积Mi
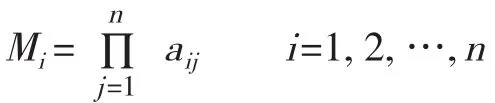
(2)计算Mi的n次方根
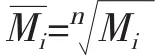

2.3.2 层次单排序一致性检验
具体步骤如下:
(1)根据判断矩阵,计算各个判断矩阵的最大特征根(λmax)
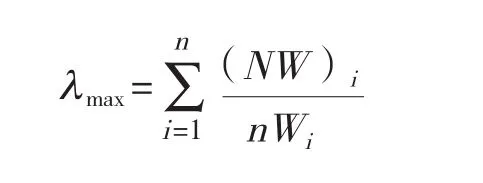
(2)计算一致性指标(CI)

(3)查表(见表9)求得平均随机一致性指标(RI)

表9 平均随机一致性指标(RI)表
(4)计算随机一致性比率(CR)

若一致性检验通过,说明各专家及执法人员的判断结果具有一致性,所计算出的各层权重值为有效;若一致性检验拒绝,则需要将判断矩阵结果返回给专家及执法人员,重新进行调整,直到通过一致性检验为止。
层次单排序一致性检验各步骤计算结果详见表10。由表可知,各判断矩阵的CR值均小于0.10,一致性检验通过。
2.4 层次总排序及其一致性检验
2.4.1 层次总排序
根据层次单排序得到的各指标的层权重,将各二级指标的层权重对应乘以一级指标的层权重,计算出各二级指标对执法能力目标而言的组合权重(见表11)。

表11 执法能力评估指标体系组合权重
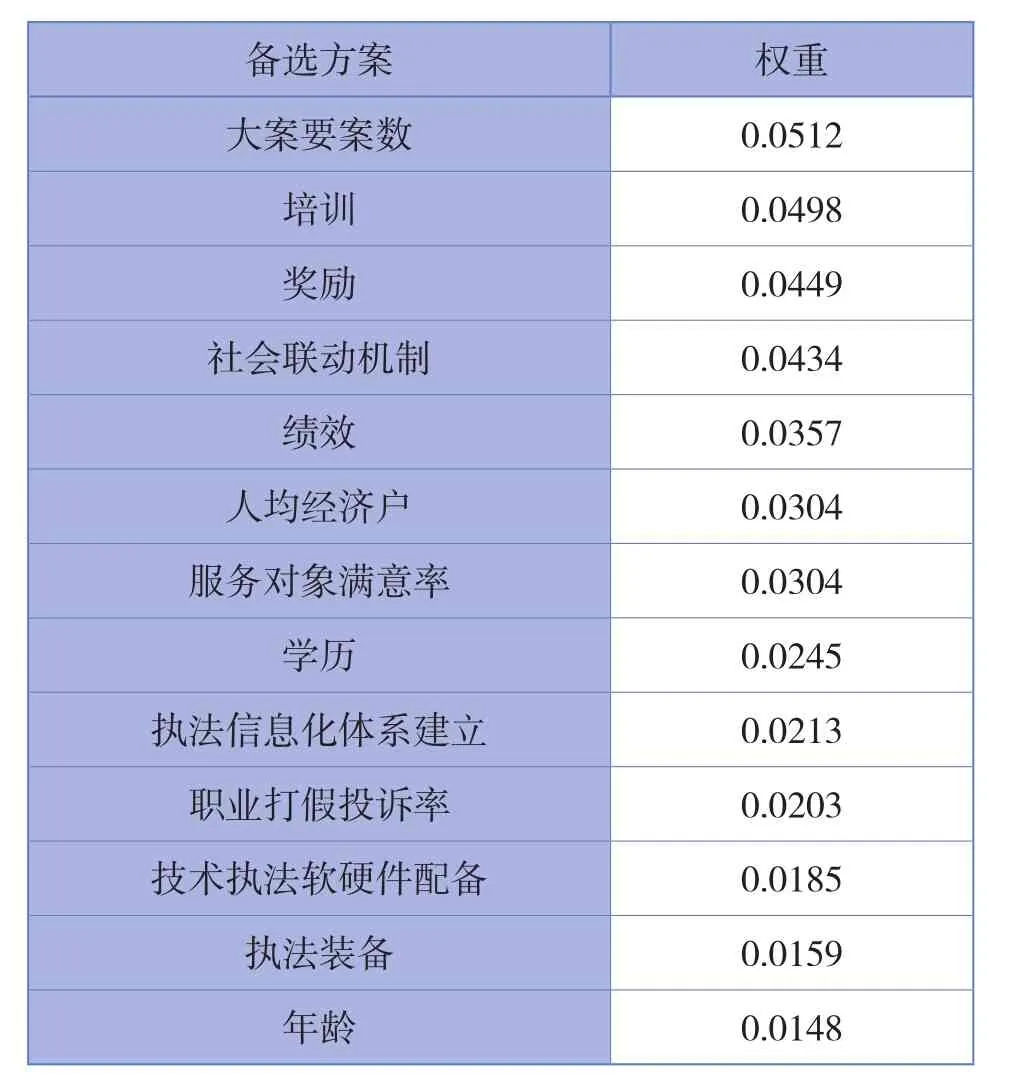
续表11
2.4.2 层次总排序一致性检验
在对同层级同类别指标作重要性比较时,通常各层级内所用的比较尺度标准基本能够保持一致,但是,一级与二级指标之间的层级差异仍可能存在,并且这种差异将随着组合权重的计算而逐渐累加起来。因此,还需要从指标体系的总体上来检验是否存在显著差异,层次总排序一致性比率(CRT)计算公式如下:
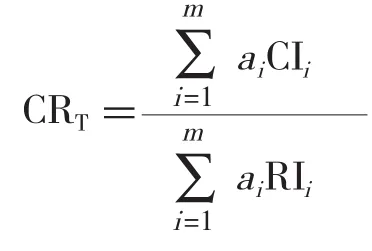
经计算层次总排序一致性比率为CRT=0.007799<0.10,通过了总体一致性检验。
3 执法能力指标评分——成熟度评价
3.1 成熟度评价基本思路
各指标按成熟度评价拟分为优、中、差三级成熟度,分别赋分值“1”“0”“-1”。目前,指标体系中以量化指标为主,仍存在少量非量化指标。对于这些非量化指标,先暂时作简单化处理,按“是/否”来分别对应“优/差”,今后将进一步研究如何将其转化为量化指标;而对于量化指标,通过研究其与执法能力的关系,发现其主要由大致三种类型凸型曲线[如B11年龄,见图2中a)]、正相关曲线[如B12执法年限,见图2中b)]、负相关曲线[如B53行政诉讼败诉率,见图2中c)],根据图2进行分析得出对应的指标值范围如下:
(1)凸型曲线:“优”对应的指标值区间为(X2,X3);“中”对应的指标值区间为[X1,X2]& [X3,X4];“差”对应的指标值区间为[0,X1)&(X4,+∞);
(2)正相关曲线:“优”对应的指标值区间为(X2,+∞);“中”对应的指标值区间为[X1,X2];“差”对应的指标值区间为[0,X1);
(3)负相关曲线:“优”对应的指标值区间为[0,X1);“中”对应的指标值区间为[X1,X2];“差”对应的指标值区间为(X2,+∞);

图2 评估指标与执法能力关系图
对各量化指标进行大样本量采样(此时,量化指标根据中心极限定理呈正态分布),进行统计可求得其正态分布参数(μ,σ)并得到概率分布函数f(x)和分布函数F(x)。
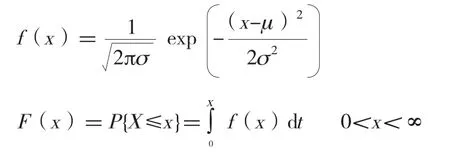
我们将优、中、差按一定比例K1∶K2∶K3(在本文中,假定按优K1=30%,中K2=40%,差K3=30%进行计算)对应选取指标值,随即可根据指标与执法能力的相关关系(凸型曲线、正相关曲线、负相关曲线),按照优中差所对应概率在正态分布曲线中对应求解指标所对应具体值范围,方法见3.2~3.4。
3.2 凸型曲线
凸型曲线正态曲线分布如图3所示。根据假设S1=S5=K3÷2=15%,S2=S4=K2÷2=20%,S3=K1=30%。
由图可知,F(X1)=S1=0.15;
F(X2)=S1+S2=0.35;
F(X3)=S1+S2+S3=0.65;
F(X4)=S1+S2+S3+S4=0.85;
则可通过反函数求得指标值范围中的参数值X1、X2、X3和X4如下:
X1=F-1(0.15)
X2=F-1(0.35)
X3=F-1(0.65)
X4=F-1(0.85)
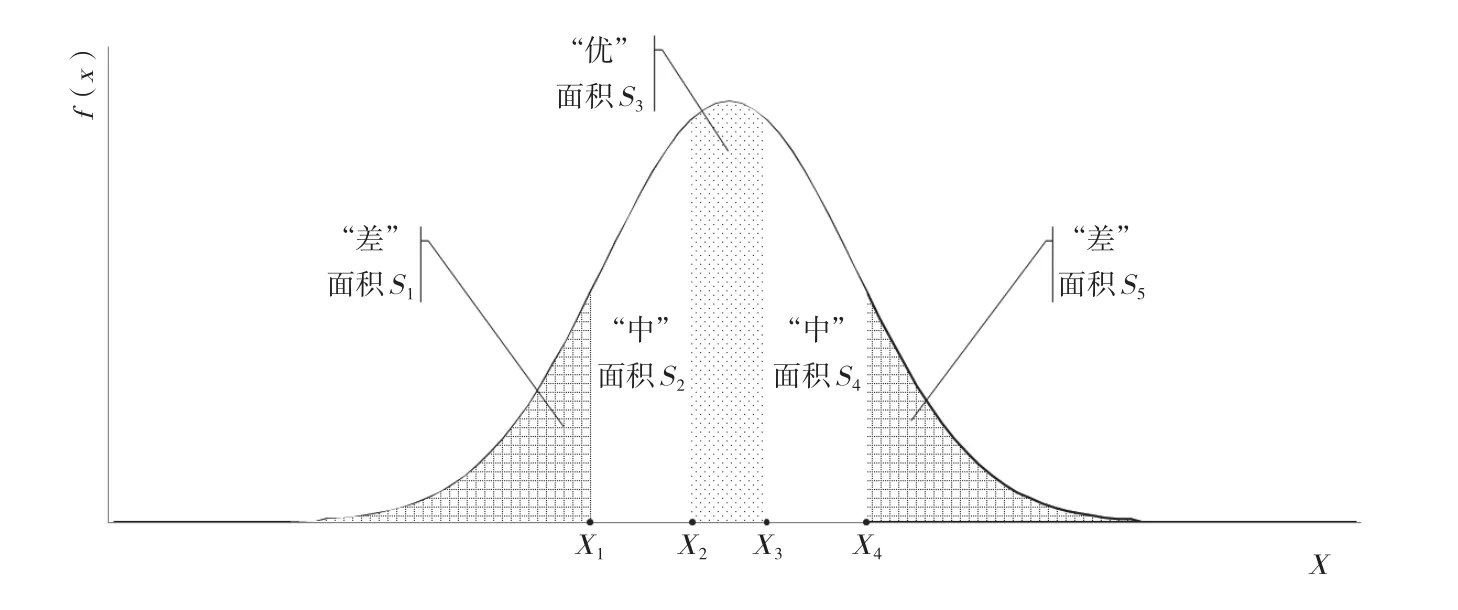
图3 凸型曲线正态曲线分布图
3.3 正相关
正相关曲线正态曲线分布如图4所示。根据假设S1=K3=30%,S2=K2=40%,S3=K1=30%。
由图可知,F(X1)=S1=0.3;
F(X2)=S1+S2=0.7;
则可通过反函数求得指标值范围中的参数值X1和X2如下:
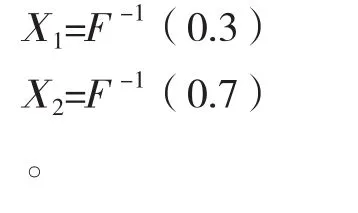
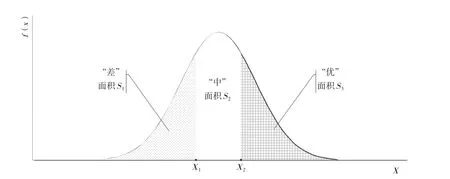
图4 正相关曲线正态曲线分布图
3.4 负相关
负相关曲线正态曲线分布如图5所示。根据假设S1=K1=30%,S2=K2=40%,S3=K3=30%。
由图可知,F(X1)=S1=0.3;
F(X2)=S1+S2=0.7;
则可通过反函数求得指标值范围中的参数值X1和X2如下:
X1=F-1(0.3)
X2=F-1(0.7)
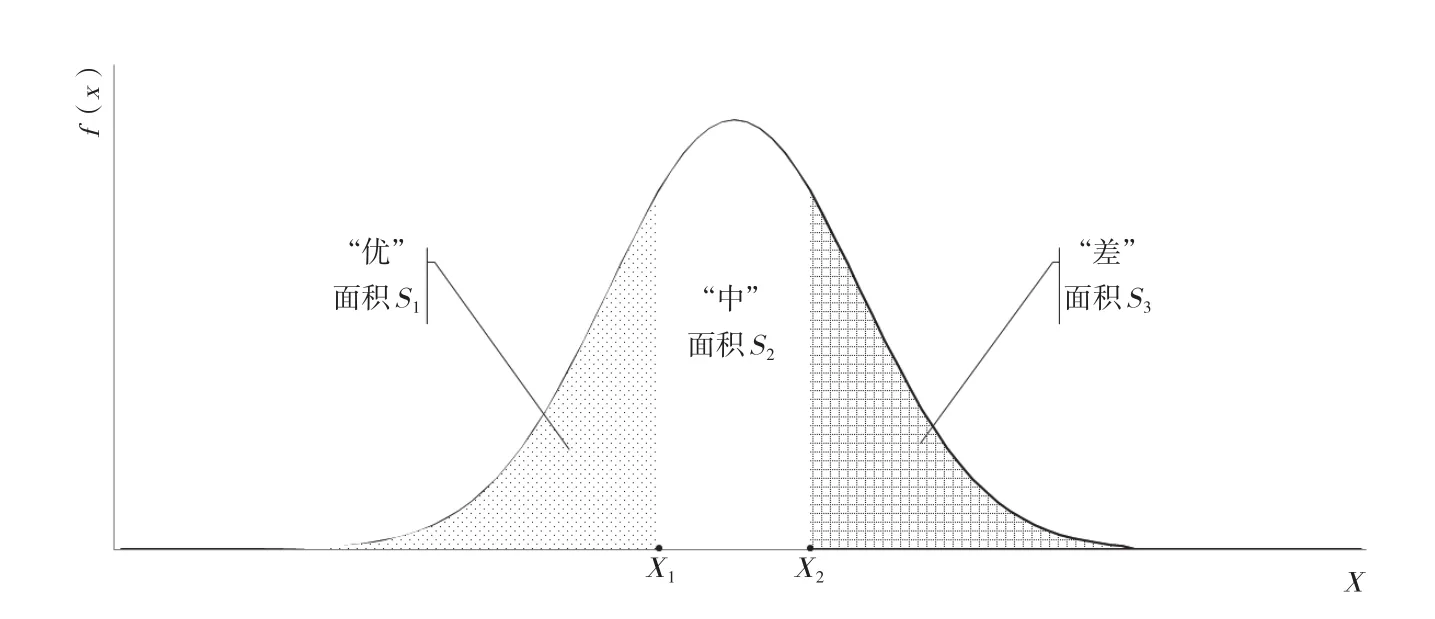
图5 负相关曲线正态曲线分布图
4 执法能力评估结果
采用线性加权方法计算得出执法能力结果,并根据需要进一步分析。执法能力(N)计算公式如下:

式中:
N ——执法能力;
λi——第i指标权重,且
Bi——第i指标成熟度评价得分。
通过N值,最终可确定评估对象目前执法能力所达到的水平等级(见表12)。

表12 执法能力水平等级
5 结语
由于目前国家深化体制改革等各方面原因,协调获取各量化指标的大范围样本数据暂时还有较大困难,导致无法求取指标正态分布曲线所对应的概率分布函数f(x)及分布函数F(x)。这也为本研究的实证验证留下了空间,下一步将通过开展全国范围内广泛调研,对指标体系进一步完善做到尽可能量化,并收集指标相关统计数据,建立执法能力基准数据库,为开展执法能力科学评估与改进奠定坚实的理论基础。
[1]Saaty T L. Decision making with the analytic hierarchy process[J]. International Journal of Services Sciences, 2008, 1(1):83-98.
[2]Aupetit B, Genest C. On some useful properties of the Perron eigenvalue of a positive reciprocal matrix in the context of the analytic hierarchy process[J].European Journal of Operational Research, 1993,70(2):263-268.
[3]田军,邹沁,汪应洛. 政府应急管理能力成熟度评估研究[J]. 管理科学学报,2014,17(11): 97-108.
Preliminary Exploration on Method of Administrative Law Enforcement Ability Assessment Based on AHP and Maturity Evaluation
Li Wei ( Shanghai Institute of Quality and Standardization )Liu Gang ( Shanghai Municipal Bureau of Quality and Technical Supervision )Jiang Ping ( Shanghai Institute of Quality and Standardization )Liu Xia, Pei Huitao ( Development Research Centre of AQSIQ )
Administrative law enforcement ability assessment could provide the scienti fi c foundation for improvement on the ef fi ciency of administrative law enforcement, and is also the important safeguard for promoting ‘government administration in accordance with the law’. In this study, we widely investigated the relevant influencing factors regarding administrative law enforcement ability during current administration system. Then, we established index system of administrative law enforcement ability assessment by Delphi method, which included personal quality &ability, motivate mechanism, social co-governance, safeguard capacity, administrative law enforcement efficiency.Finally, we creatively proposed the general idea for assessment that adopted AHP to calculate index weight and used maturity evaluation method to get index score. This study laid a useful theoretical foundation for establishment of administrative law enforcement ability assessment system.
administrative law enforcement ability, AHP, maturity evaluation, assessment model
1)基金项目:本文系质检总局科技计划项目“质监体制机制改革与基层能力建设”(计划编号:2016QK012)阶段性研究成果。

